Золотое сечение да винчи: Золотое сечение как объяснение пропорций красоты

Золотое сечение как объяснение пропорций красоты

Над чем работают лучшие умы современной стоматологической науки? Над идеальной улыбкой, воплотившей в себе красоту и здоровье.

Что такое «красота»? Почему лицо и облик одного человека нам нравится, а другого — нет?

На эти вопросы пытались ответить учёные ещё тогда, когда не было ни только стоматологии как направления медицины, но и сама медицина находилась в стадии зарождения.

Оказывается, наше лицо и тело имеет определённые пропорции, кажущиеся на первый взгляд почти мистическими.

Хотя в наш просвещённый век многому можно найти научное и даже математическое объяснение.

Принято считать, что впервые закономерности соотношение размеров тела человека и отдельных его частей обобщил и сформулировал в 1855 г. немецкий исследователь Цейзинг в своём научном труде «Эстетические исследования». За основу своей теории он взял учение о «золотом сечении».

Ещё в VI веке до н.э. древнегреческий философ и математик Пифагор ввёл в научный обиход понятие «золотое деление».

«Золотое деление» — это пропорциональное деление отрезка на неравные части. При этом меньший отрезок так относится к большему, как больший отрезок относится ко всему отрезку. a : b = b : c или с : b = b : а.

Так что же особенного в этом соотношении?

Оказывается, что всегда меньший отрезок относится к большему, как 0,382: к 0,618:

То есть, если АВ принять за единицу, АЕ/ЕВ=0,62/0,32 (в практических целях используют приближённые значения).

Один из примеров «золотого деления», с которым наверняка все знакомы, это — пентаграмма и, как представители её, так любимые людьми старшего поколения, «знак качества» и «звезда».

Все диагонали пятиугольника (пятиугольная звезда) делят друг друга на отрезки, связанные между собой «золотой пропорцией».

В настоящее время эта математическая закономерность носит название «золотое сечение», которое ввел в обиход ещё Леонардо да Винчи, который проводил сечения стереометрического тела, образованного правильными пятиугольниками.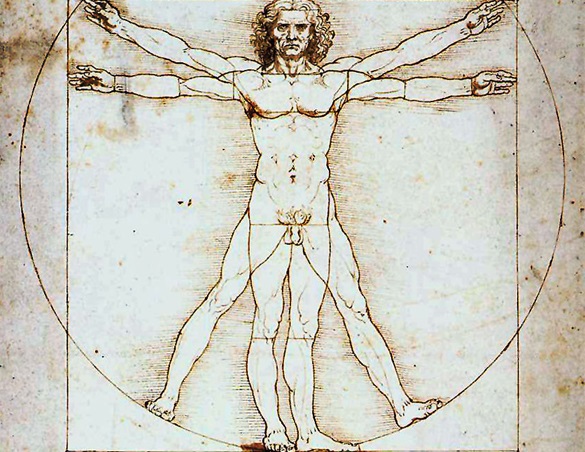 И каждый раз он получал соотношение сторон в «золотом делении». Он дал этому делению название «золотое сечение», принятое до сих пор.

Но не Пифагор впервые обнаружил закономерность «золотого сечения». Ещё древние египтяне и вавилоняне использовали эти знания в строительстве пирамид и изготовлении предметов обихода. Древние греки при проектировании своих зданий использовали пропорции «золотого сечения». В эпоху возрождения интерес к «золотому сечению» усилился. Художники нашли применение ему в искусстве. Учение о «золотом сечении» связано с именем гениального итальянского математика и монаха Луки Пачоли. В 1509 г. Была издана его книга «Божественная пропорция» с иллюстрациями Леонардо да Винчи (предположительно). Он причислял золотую пропорцию к «божественной сути» через триединство: бог сын, бог отец и святой дух, находящихся между собой в «золотой пропорции».

История «золотого сечения» связана ещё с одним известным итальянским математиком Фибоначчи. До наших времён дошёл ряд чисел: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55 и т. д., известный, как ряд Фибоначчи.

Особенность последовательности данных чисел заключается в том, что каждый её член, начиная с третьего, равен сумме двух предыдущих (2+3=5, 3+5=8), а отношение смежных чисел ряда приближается к отношению «золотого сечения» (21:34=0,617, а 34:55=0,618). В последствии все исследователи «золотого сечения» в растительном и животном мире, искусстве и анатомии приходили к этому ряду, как арифметическому выражению закона золотого деления. Интересно, что свой закон Фибонначи вывел, подсчитывая количество рождённых кроликов от пары кроликов за год.

Так в чём же ореол таинственности «золотого сечения»?

Всё, что растёт и приобретает какую-либо форму в живом мире нашей планеты — растёт вверх или закручивается по спирали. Спираль (например, морская раковина) — пример соотношения в пропорциях «золотого сечения». Спирали прослеживаются в расположении семян в шишках хвойных деревьев, в семенах подсолнечника и др.

Паук плетёт паутину по спирали, ДНК человека закручено по спирали.

А рост вверх? Растение живёт по тем же законам «золотого сечения». Самый большой участок стебля — до первого листочка. Затем следующие сегменты уменьшаются в пропорции «золотого сечения»: с : в = в : а

Удивительно то, что и человек в соотношении отдельных частей тела и расстояний между ними, подчиняется законам «золотого сечения».

Немецкий учёный Альберт Дюрер доказал, что рост человека делится в золотых пропорциях линией, проходящей через пупок и линией, проходящей через кончики средних пальцев опущенных рук.

Его труды продолжил Цейзинг. Он выяснил, что пропорции мужского тела колеблются в пределах 13 : 8 = 1, 625.

А пропорции женского тела в среднем находятся в соотношении 8 : 5 = 1,6.

Пропорции «золотого сечения» проявляются в отношении длины плеча, предплечья, кисти и пальцев и т.д.

Поразительно, но в лице человека можно проследить множество пропорций, подчиненных «золотому сечению». Причем, чем больше в лице человека соотношений в этой пропорции, тем красивее нам он кажется. Есть лица, при характеристике которых употребляют выражение «правильные черты лица». У этих людей основные пропорции наиболее близки к соотношению 1, 618: или 62 : 38.

Какие же пропорции в лице человека стремятся к «золотому сечению»?

Прежде всего, у людей с красивыми лицами наблюдается:

1. Идеальная пропорция между расстояниями от медиального угла глаза до крыла носа и от крыла носа до подбородка. Это соотношение называется «динамической симметрией» или «динамическим равновесием».
2. Соотношение высоты верхней и нижней губы будет 1,618.
3. Высота надгубной складки (расстояние между верхней губой и нижней границей носа) и высота губ будут составлять соотношение 62 : 38.
4. Ширина одной ноздри суммарно с шириной переносицы относится к ширине другой ноздри в пропорции «золотого сечения».
5. Ширина ротовой щели также относится к ширине между наружными краями глаз, а расстояние между наружными уголками глаз — к ширине лба на уровне линии бровей, как все пропорции «золотого сечения».
6. Расстояние между линии смыкания губ до крыльев носа относится к расстоянию от линии смыкания губ до нижней точки подбородка, как 38 : 62: И к расстоянию от крыльев носа до зрачка — как 38 : 62 = 0.
7. Расстояние между линией верхней части лба до линии зрачков и расстояние между линией зрачков и линией смыкания губ имеет пропорцию «золотого сечения».

Можно продолжить этот список соотношения размеров гармоничного лица. Получается, правильную красоту можно математически просчитать и даже прибегнуть к хирургической корректировке с целью совершенствования внешности.

В настоящее время стоматология, наряду с пластической хирургией, занимается не только лечением заболеваний полости рта, но и эстетической медициной.

Удивительно, но и в стоматологии можно проследить пропорции «золотого сечения».

Красивая улыбка — это не только белоснежные здоровые ровные зубы, но и их правильное соотношение и расположение. И здесь мы опять сталкиваемся с закономерность «золотого сечения».

Вот некоторые примеры соотношений размеров и расстояний между зубами:

1. Ширина верхнего центрального резца относится к ширине нижнего центрального резца, как 62 : 38, т.е. 1, 618:, в соотношении «золотого сечения».
2. В этой же пропорции находится ширина двух верхних резцов к ширине двух нижних.
3. Расстояние между премолярами верхней челюсти относится к ширине четырёх верхних резцов, как 62 : 38.
4. Расстояние между дистальными поверхностями нижних клыков и щечными фиссурами моляров — пропорция 38 : 62.

И этот список можно продолжить.

Как же на практике можно использовать знание о «золотом сечении» и его влиянии на параметры в стоматологии?

Разумеется, искать применение золотых пропорций в эстетической стоматологии.

Расположение, размер и взаимное соотношение зубов в полости рта — всё это подчинено общему закону — «золотому сечению».

Вольно или невольно, осознанно или неосознанно врач использует эти пропорции при восстановлении коронковой части зуба, при протезировании или ортодонтических мероприятиях. Лучше, конечно, чтобы врач применял математическую составляющую в формировании вашей красоты и здоровья.

А мы теперь знаем, что человек — только часть живого мира на нашей планете, подчиняющийся общим законам мироздания. И доказательство тому — учение о «золотом сечении», дошедшее до нас уже даже не из предыдущего тысячелетия.

Время работы

Пн-Пт	10:00 — 22:00
Сб-Вс	10:00 — 20:00

Круковская Наталья Владимировна Врач дерматокосметолог

Золотое сечение Да Винчи: как это работает. 1,6180339887… | Такая неизвестная Земля

«Я не знаток, я просто врач, но я много думал над вопросами анатомии. Если упростить определение, которое на самом деле гораздо сложнее, как и вообще всё в мире, то надо сказать, прежде всего, что красота существует как объективная реальность, а не создаётся в мыслях и чувствах человека.

…Красота – это наивысшая степень целесообразности, степень гармонического соответствия и сочетания противоречивых элементов во всяком устройстве, во всякой вещи, всяком организме. А восприятие красоты нельзя никак иначе себе представить, как инстинктивное …»

Иван Ефремов, Лезвие бритвы, глава III.

+++

Золотое сечение — это универсальное проявление структурной гармонии. Оно встречается в природе, науке, искусстве – во всем, с чем может соприкоснуться человек. Однажды познакомившись с золотым правилом, человечество больше ему не изменяло.

Интересно Знать рассказывает:

Наиболее емкое определение золотого сечения гласит, что меньшая часть относится к большей, как большая ко всему целому. Приблизительная его величина – 1,6180339887. В округленном процентном значении пропорции частей целого будут соотноситься как 62% на 38%. Это соотношение действует в формах пространства и времени.

Древние видели в золотом сечении отражение космического порядка, а Иоганн Кеплер называл его одним из сокровищ геометрии. Современная наука рассматривает золотое сечение как «ассиметричную симметрию», называя его в широком смысле универсальным правилом отражающим структуру и порядок нашего мироустройства.

Представление о золотых пропорциях имели древние египтяне, знали о них и на Руси, но впервые научно золотое сечение объяснил монах Лука Пачоли в книге «Божественная пропорция» (1509), иллюстрации к которой предположительно сделал Леонардо да Винчи. Пачоли усматривал в золотом сечении божественное триединство: малый отрезок олицетворял Сына, большой – Отца, а целое – Святой дух.

Непосредственным образом с правилом золотого сечения связано имя итальянского математика Леонардо Фибоначчи. В результате решения одной из задач ученый вышел на последовательность чисел, известную сейчас как ряд Фибоначчи: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34,  … и т.д. На отношение этой последовательности к золотой пропорции обратил внимание Кеплер: «Устроена она так, что два младших члена этой нескончаемой пропорции в сумме дают третий член, а любые два последних члена, если их сложить, дают следующий член, причем та же пропорция сохраняется до бесконечности». Сейчас ряд Фибоначчи это арифметическая основа для расчетов пропорций золотого сечения во всех его проявлениях.

Леонардо да Винчи также много времени посвятил изучению особенностей золотого сечения, скорее всего именно ему принадлежит и сам термин. Его рисунки стереометрического тела, образованного правильными пятиугольниками, доказывают, что каждый из полученных при сечении прямоугольников дает соотношения сторон в золотом делении.

Со временем правило золотого сечения превратилось в академическую рутину, и только философ Адольф Цейзинг в 1855 году вернул ему вторую жизнь. Он довел до абсолюта пропорции золотого сечения, сделав их универсальными для всех явлений окружающего мира. Впрочем, его «математическое эстетство» вызывало много критики.

Даже не вдаваясь в расчеты, золотое сечение можно без труда обнаружить в природе. Так, под него попадают соотношение хвоста и тела ящерицы, расстояния между листьями на ветке, есть золотое сечение и в форме яйца, если условную линию провести через его наиболее широкую часть.

Белорусский ученый Эдуард Сороко, который изучал формы золотых делений в природе, отмечал, что все растущее и стремящееся занять свое место в пространстве, наделено пропорциями золотого сечения. По его мнению, одна из самых интересных форм это закручивание по спирали.

Еще Архимед, уделяя внимание спирали, вывел на основе ее формы уравнение, которое и сейчас применяется в технике. Позднее Гете отмечал тяготение природы к спиральным формам, называя спираль «кривой жизни». Современными учеными было установлено, что такие проявления спиральных форм в природе как раковина улитки, расположение семян подсолнечника, узоры паутины, движение урагана, строение ДНК и даже структура галактик заключают в себе ряд Фибоначчи.

Человек

Модельеры и дизайнеры одежды все расчеты делают, исходя из пропорций золотого сечения. Человек – это универсальная форма для проверки законов золотого сечения. Конечно, от природы далеко не у всех людей пропорции идеальны, что создает определенные сложности с подбором одежды.

В дневнике Леонардо да Винчи есть рисунок вписанного в окружность обнаженного человека, находящегося в двух наложенных друг на друга позициях. Опираясь на исследования римского архитектора Витрувия, Леонардо подобным образом пытался установить пропорции человеческого тела. Позднее французский архитектор Ле Корбюзье, используя «Витрувианского человека» Леонардо, создал собственную шкалу «гармонических пропорций», повлиявшую на эстетику архитектуры XX века.

Адольф Цейзинг, исследуя пропорциональность человека, проделал колоссальную работу. Он измерил порядка двух тысяч человеческих тел, а также множество античных статуй и вывел, что золотое сечение выражает среднестатистический закон. В человеке ему подчинены практически все части тела, но главный показатель золотого сечения это деление тела точкой пупа.

В результате измерений исследователь установил, что пропорции мужского тела 13:8 ближе к золотому сечению, чем пропорции женского тела – 8:5.

Искусство пространственных форм

Художник Василий Суриков говорил, «что в композиции есть непреложный закон, когда в картине нельзя ничего ни убрать, ни добавить, даже лишнюю точку поставить нельзя, это настоящая математика». Долгое время художники следователи этому закону интуитивно, но после Леонардо да Винчи процесс создания живописного полотна уже не обходится без решения геометрических задач. Например, Альбрехт Дюрер для определения точек золотого сечения использовал изобретенный им пропорциональный циркуль.

Искусствовед Ф. В. Ковалев, подробно исследовав картину Николая Ге «Александр Сергеевич Пушкин в селе Михайловском», отмечает, что каждая деталь полотна будь-то камин, этажерка, кресло или сам поэт строго вписаны в золотые пропорции.

Исследователи золотого сечения без устали изучают и замеряют шедевры архитектуры, утверждая, что они стали таковыми, потому что созданы по золотым канонам: в их списке Великие пирамиды Гизы, Собор Парижской Богоматери, Храм Василия Блаженного, Парфенон.

И сегодня в любом искусстве пространственных форм стараются следовать пропорциям золотого сечения, так как они, по мнению искусствоведов, облегчают восприятие произведения и формируют у зрителя эстетическое ощущение.

Слово, звук и кинолента

Формы временного искусства по-своему демонстрируют нам принцип золотого деления. Литературоведы, к примеру, обратили внимание, что наиболее популярное количество строк в стихотворениях позднего периода творчества Пушкина соответствует ряду Фибоначчи – 5, 8, 13, 21, 34.

Действует правило золотого сечения и в отдельно взятых произведениях русского классика. Так кульминационным моментом «Пиковой дамы» является драматическая сцена Германа и графини, заканчивающаяся смертью последней. В повести 853 строки, а кульминация приходится на 535 строке (853:535=1,6) – это и есть точка золотого сечения.

Советский музыковед Э. К. Розенов отмечает поразительную точность соотношений золотого сечения в строгих и свободных формах произведений Иоганна Себастьяна Баха, что соответствует вдумчивому, сосредоточенному, технически выверенному стилю мастера. Это справедливо и в отношении выдающихся творений других композиторов, где на точку золотого сечения обычно приходится наиболее яркое или неожиданное музыкальное решение

Кинорежиссер Сергей Эйзенштейн сценарий своего фильма «Броненосец Потёмкин» сознательно согласовывал с правилом золотого сечения, разделив ленту на пять частей. В первых трех разделах действие разворачивается на корабле, а в последних двух – в Одессе. Переход на сцены в городе и есть золотая середина фильма.

Леонардо да Винчи, золотое сечение: кратко об идеале форм

Сознание человека неустанно стремится к идеалу. Высота это непокорима, ведь тайна идеального не разгадана. Одой из сторон идеального в нашем мире занимался Леонардо да Винчи. Золотое сечение, ставшее темой нашей статьи, тесно связывают с именем этого гения.

Золотое сечение — тайны нашего сознания?

Хоть мы и считаем свои действия полностью осознанными, задумываясь над некоторыми повседневными поступками, можем в этом усомниться.

Так, например, представим обычную скамейку в парке, на которую мы желаем присесть. Куда мы сядем? В центре скамейки или прижмемся к краю? Почти наверняка произойдет третий вариант. Мы сядем так, чтобы соотношение образовавшихся частей скамейки было около 1,62. Так мы будем ощущать себя комфортнее, в мыслях и чувствах будет гармония. Это — тяготение человека к идеальному. Это — достигнутое золотое сечение.

Об идеальных пропорциях во всем, что нас окружает, много рассуждали мудрецы древности. Египтяне, индийцы, китайцы — такие разные давние цивилизации, а представления об идеале сходилось именно к золотому сечению. Греческий математик и философ Пифагор основал школу, посвященную сути золотого сечения. Даже понятия этики Аристотелем были сопоставлены с идеальной гармонией.

В Средние века на сущность идеального обратил свое внимание гениальный механик, ученый и художник Леонардо да Винчи. Золотое сечение, отображенное им во всемирно известном изображении «витрувианского человека».

Наследуя высшую гармонию

Известные художники много взяли из опыта античных мастеров. Микеланджело и Леонардо да Винчи золотое сечение воплощали в своих полотнах. По мнению творцов, соблюдая нужные пропорции, можно достичь красоты в картине.

То же мы наблюдаем в образцах древней архитектуры. Повсеместно в разных уголках планеты различные цивилизации придерживались одних пропорций.

Появление термина

Появление термина «золотое сечение» приписывается трудам Пифагора (6 век до н. э.). Он же, в свою очередь, перенял учение об идеальных пропорциях у более древних народов — вавилонян, египтян.

Впервые золотое сечение упоминает в своих «Началах» Эвклид. В одной из книг он подает геометрическую схему построения золотого деления. После него идеальными пропорциями фигур занимался Гипискл во 2 веке до н. э. В Европу эти знания пришли в Средние века через арабский перевод Эвклидовых «Начал».

Наваррский переводчик текстов Дж. Кампано написал свои комментарии к переводному тексту «Начал». Видимо, в нем отображались значительные тайны нашей жизни, способные повлиять на нее. Информация о золотом сечении в Европе некоторое время была доступна лишь избранным.

«Витрувианский человек»

Имя и достижения Марка Витрувия сегодня известны немногим, несмотря на все его открытия. Насмешка судьбы в том, что если бы да Винчи не изобразил иллюстрацию к тому, что писал в своих «Десяти книгах» римлянин о пропорциях тела человека, то Витрувия бы могли забыть вовсе.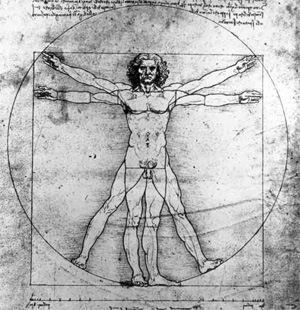 Таким образом гений одного увековечил гений другого.

Представляемое золотое сечение Леонардо да Винчи — пропорции человеческого тела, которое можно вписать в геометрические фигуры-символы (квадрат и круг, о коих уже шла речь). Изображение «витрувианского человека» — это и есть зашифрованное золотое сечение, по мнению исследователей вопроса. Мы знаем, что даже свои записи да Винчи любил кодировать, так и с ключом к разгадке идеальных пропорций.

Золотое сечение Леонардо да Винчи: что кроется в шифре?

В изображении «витрувианского человека» принято усматривать два тела — две фигуры, одна из которых вписывается в круг, а другая — в квадрат. Толкование такой композиции имеет следующее значение.

Квадрат — символ земного, таким образом автор отображает привязанность человека к земному, материальному. Центр квадрата находится в паховой области.

Круг — символ божественного, в том числе и божественного происхождения человека. Фигура, находящаяся в круге, не содержит черточек, то есть не измеряется. Поскольку как явление божественное, эта фигура и не может быть измерена. Центр окружности — пупок человека.

По современным представлениям, видеть только две фигуры в «витрувианском человеке» — слишком плоско. На самом деле в изображении можно рассмотреть гораздо больше. И это еще не все тайны, разгадываемые в этой загадке.

Внимание также обращается к ногам фигуры, стоящей в круге (божественное начало). Они стоят на плоскости, выходят за рамки окружности. В этом видится символ того, что человек тяготеет к земному, несмотря на божественную свою составляющую.

По материалам, оставленным Леонардо да Винчи, золотое сечение, кратко говоря, усматривается в человеческом теле. И опять-таки в изображении «витрувианского человека» заключено устремление людей того времени к возвышению. Великий гений узрел и попытался передать другим поколениям глубокий смысл, увиденный им в нашей природе.

Еще одно знаменитое творение, в котором отобразил Леонардо да Винчи золотое сечение, — «Мона Лиза».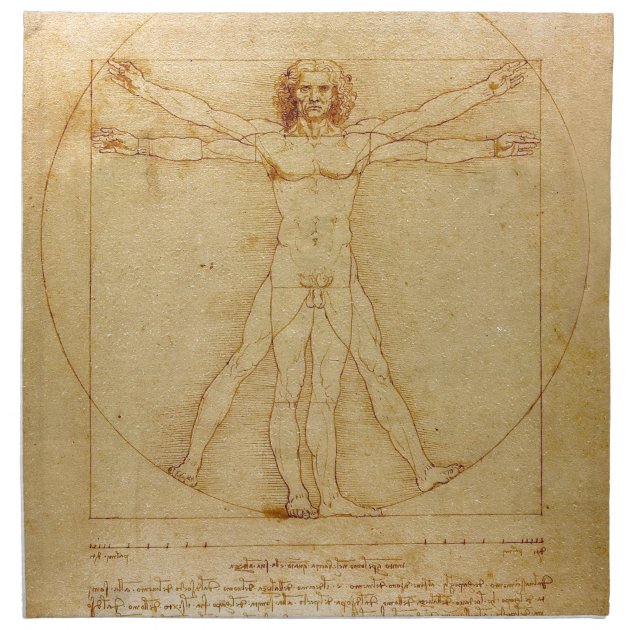 Ее загадочная улыбка невероятным образом очаровывает миллионы созерцателей.

Истоки появления рисунка «Витрувианский человек»

В очень давние, но незабытые времена, в 1 веке до нашей эры, римлянин Витрувий создал свои «Десять книг» — труд, посвященный императору Августу. Но, кроме благодарности за помощь, в книгах содержатся ценнейшие советы в области архитектуры.

Книги Витрувия не стали известными при жизни автора. Зато примечателен факт, что именно он завел речь об эстетике архитектуры, эргономике конструкций. Последнее крайне важно, поскольку в наше время инженеры и архитекторы проектируют свои творения, опираясь на данные человеческого тела, чтобы сделать использование конструкций удобным. Кроме того, Витрувий спроектировал акведук — водоснабжающие системы, значительно улучшившие жизнь в римских городах.

А вот одна из «Десяти книг» Витрувия посвящена человеческому телу. Впервые поднимался вопрос о пропорциях и некоем делении, делающем его близким к идеалу. Гласила эта книга о том, что человек идеально вписывается в квадратную форму.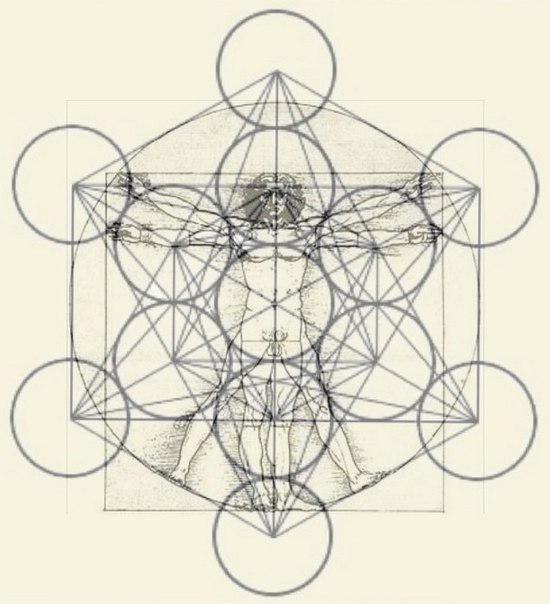 Последняя же — отображение сущности всего земного. Также человека можно вписать и в круг — символ божественного. Таким образом человек приближается к Богу, и такие философствования близки духу той эпохи.

Посмотрите еще раз на то, как изобразил золотое сечение Леонардо да Винчи. Картинки, которые можно найти во многих книгах, дают возможность ознакомиться с шифром и попытаться увидеть разгадку формулы.

Джакомо Андреа и да Винчи: кто истинный создатель?

Знаменитое изображение «витрувианского человека» да Винчи получило грандиозную популярность. Но, как свидетельствуют разные исторические источники, возможно, идея отыскать золотое сечение человеческого тела была вовсе не Леонардо. Здесь важную роль сыграл друг художника — Джакомо Андреа, чья судьба была крайне трагична.

Джакомо также была сделана иллюстрация к книге Витрувия, отображающая линии идеального деления тела человека. Если сравнить ее с творением да Винчи, сходство будет замечено сразу же. Но это еще не все факты.

На найденном изображении исследователи увидели правки: кто-то корректировал его, по всей видимости, доводя до своего субъективного идеала. Кроме того, изображение авторства Джакомо Андреа старше, чем Леонардо да Винчи. Плюс творение последнего создавалось «начисто», без поправок, с легкой руки. Так, словно его делали по памяти.

Однако же так разворачивались события по мнению историков-искусствоведов, коим более интересны разные страсти, что кипели в науке и искусстве того времени. О гениальности художника и ученого Леонардо да Винчи, золотое сечение в представлении которого мы и рассматриваем, спорить не приходится, поэтому неудивительно, что его «Витрувианский человек» нарисован с первого раза.

Золотое сечение в обычных и необычных вещах

В неживой природе формула золотого сечения не просматривается. Зато все живое, созданное природой, неуклонно следует закону красоты. Если оглянуться вокруг, то увидим, что самые привлекательные и радующие нас явления соответствуют пропорции золотого сечения: от лепестков цветка, морской раковины с множеством завитков, уменьшающихся к центру как раз на нужное значение, до красивого человеческого тела, на котором так гениально продемонстрировал золотое сечение Леонардо да Винчи.

Принципы золотого деления наследуют и современные художники, фотографы, скульпторы и дизайнеры. Оно по сей день до конца не понято, но его применение делает любую вещь гораздо привлекательнее. В этом его грандиозная эстетическая составляющая.

Заключение

Тайна золотого сечения — высшей гармонии, дарующей красоту, проста и недосягаема в одночасье. Его воплощенную суть мы видим в повседневной нашей жизни и в простых естественных вещах, на которые привыкли не обращать внимания.

Великие умы, самые ярые искатели тайн бытия, такие как Эйнштейн, разгадывали точное значение золотого деления. Однако далее, чем бесконечное количество цифр после нуля, еще никто не продвинулся… Так какие же выводы делать нам? Как раз те, о которых твердит мудрость веков: ничто не идеально. Но к идеальному нужно стремиться ради создания высшей красоты, раскрытия тайны этого мира и нашего с вами сознания.

Витрувианский человек. Золотое сечение. — toomth — LiveJournal

Витрувианский человек — рисунок, сделаный Леонардо Да Винчи примерно в 1490-1492 годах, как иллюстрация для книги, посвященной трудам Витрувия. Рисунок сопровождается пояснительными надписями, в одном из его журналов. На нем изображена фигура обнаженного мужчины в двух наложенных одна на другую позициях: с разведенными в стороны руками, описывающими круг и квадрат.

Рисунок и текст иногда называют каноническими пропорциями. При исследовании рисунка можно заметить, что комбинация рук и ног в действительности составляет четыре различных позы. Поза с разведенными в стороны руками и не разведенными ногами, вписывается в квадрат («Квадрат Древних»). С другой стороны, поза с раскинутыми в стороны руками и ногами, вписывается в круг. И, хотя, при смене поз, кажется, что центр фигуры движется, на самом деле, пуп фигуры, который является настоящим её центром, остается неподвижным.

«Vetruvio architetto mette nelle sue opera d’architettura che le misure dell’omo…» «Архитектор Ветрувий заложил в своей архитектуре измерения человека…» Далее идет описание соотношений между различными частями человеческого тела.

В сопроводительных записях Леонардо да Винчи указал, что рисунок был создан для изучения пропорций (мужского) человеческого тела, как оно описано в трактатах античного римского архитектора Витрувия (Vitruvius), который написал следующее о человеческом теле:

«Природа распорядилась в строении человеческого тела следующими пропорциями:

длина четырёх пальцев равна длине ладони,
четыре ладони равны стопе,
шесть ладоней составляют один локоть,
четыре локтя — рост человека.
Четыре локтя равны шагу, а двадцать четыре ладони равны росту человека.
Если вы расставите ноги так, чтобы расстояние между ними равнялось 1/14 человеческого роста, и поднимите руки таким образом, чтобы средние пальцы оказались на уровне макушки, то центральной точкой тела, равноудаленной от всех конечностей, будет ваш пупок.
Пространство между расставленными ногами и полом образует равносторонний треугольник.
Длина вытянутых рук будет равна росту.
Расстояние от корней волос до кончика подбородка равно одной десятой человеческого роста.
Расстояние от верхней части груди до макушки составляет 1/6 роста.
Расстояние же от верхней части груди до корней волос — 1/7.
Расстояние от сосков до макушки составляет ровно четверть роста.
Наибольшая ширина плеч — восьмая часть роста.
Расстояние от локтя до кончиков пальцев — 1/5 роста, от локтя до подмышечной ямки — 1/8.
Длина всей руки — это 1/10 роста.
Начало гениталий находится как раз посредине тела.
Стопа — 1/7 часть роста.
Расстояние от мыска ноги до коленной чашечки равно четверти роста, а расстояние от коленной чашечки до начала гениталий также равно четверти роста.
Расстояние от кончика подбородка до носа и от корней волос до бровей будет одинаково и, подобно длине уха, равно 1/3 лица.»

Повторное открытие математических пропорций человеческого тела в XV веке, сделанное Леонардо Да Винчи и другими, стало одним из великих достижений, предшествующих итальянскому ренессансу. Рисунок сам по себе часто используется как неявный символ внутренней симметрии человеческого тела.

Искусству присуще стремление к стройности, соразмерности, гармонии. Мы находим их в пропорциях архитектуры и скульптуры, в расположении предметов и фигур, сочетании красок в живописи, в чередовании рифм и мерности ритма в поэзии, в последовательности музыкальных звуков. Эти свойства не выдуманы людьми. Они отражают свойства самой природы. Одна из пропорций чаще всех встречается в искусстве. Она получила название «золотое сечение». Золотое сечение было известно ещё в древности. Так в книге II „Начал” Евклида оно применяется при построении пяти- и десятиугольников.

Термин «золотое сечение» ввел Леонардо да Винчи. Если человеческую фигуру — самое совершенное творение вселенной — перевяжем поясом и отмерим потом расстояние от пояса до ступней, то эта величин будет относиться к расстоянию от того же пояса до макушки, как весь рост человека относится к длине от пояса до ступней…

Действительно в природе и человеческом теле много пропорциональных отношений, близких к тому, которое Леонардо да Винчи назвал золотым сечением. Хотя и не воплощающих его точно. Кстати, золотое сечение, предпочтительное во многих случаях, не единственное отношение, зрительно воспринимаемое как красивое. К их числу относятся такие отношения, как 1:2, 1:3. Они близки к золотому сечению. В любом произведении искусства несколько неравных, но близких к золотому сечению частей дают впечатление развития форм, их динамики, пропорционального дополнения друг другу.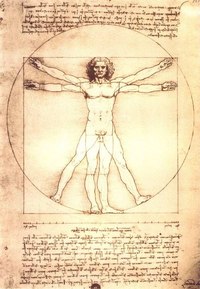 В частности, наиболее распространено отношение на основе золотого сечения при возведении памятников.

А можно ли говорить о золотом сечении в музыке? Можно, если «измерять» музыкальное произведение по времени его исполнения. В музыке золотое сечение отражает особенности человеческого восприятия временных пропорций. Точка золотого сечения служит ориентиром формообразования (особенно в небольших сочинениях), часто на неё приходится кульминация. Это может быть также самый яркий момент или самый тихий, самое плотное по фактуре место или самое звуковысотное. Но случается и так, что в точке золотого сечения появляется новая музыкальная тема.

15 малоизвестных фактов о «Витрувианском человеке» Леонардо да Винчи

1. Леонардо никогда не собирался выставлять своего «Витрувианского человека» напоказ

Эскиз был обнаружен в одной из личных записных книжек мастера эпохи Возрождения. На самом деле Леонардо нарисовал эскиз для собственных исследований и даже не подозревал о том, что им когда-то будут восхищаться. Тем не менее, сегодня «Витрувианский человек» является одной из самых известных работ художника, наряду с «Тайной вечерей» и «Моной Лизой».

2. Сочетание искусства и науки

Будучи истинным представителем эпохи Возрождения, Леонардо был не только живописцем, скульптором и писателем, но также изобретателем, архитектором, инженером, математиком и знатоком анатомии. Этот рисунок, выполненный чернилами, стал результатом изучения Леонардо теорий о человеческих пропорциях, описанных древнеримским архитектором Витрувием.

3. Леонардо не первый пытался проиллюстрировать теории Витрувия

4. Возможно, рисунок был сделан не только самим Леонардо

В 2012 году итальянский историк архитектуры Клаудио Сгарби опубликовал выводы, что исследование Леонардо относительно пропорций тела человека было вызвано аналогичным исследованием, проделанным его другом и коллегой-архитектором Джакомо Андреа де Феррара. До сих пор неясно, работали ли они вместе. Даже если эта теория неверна, историки согласны в том, что Леонардо усовершенствовал недостатки работы Джакомо.

5. Круг и квадрат имеют свой скрытый смысл

В своих математических исследованиях Витрувий и Леонардо описывали не только пропорции человека, но и пропорции всего творения. В записной книжке 1492 года была найдена запись Леонардо: «Древний человек был миром в миниатюре. Поскольку человек состоит из земли, воды, воздуха и огня, его тело напоминает микрокосм Вселенной».

6. «Витрувианский человек» — только один из многих набросков

Для того, чтобы усовершенствовать свое искусство и лучше понять, как устроен мир вокруг него, Леонардо нарисовал много людей, чтобы сложить представление об идеальных пропорциях.

7. Витрувианский человек — идеал мужчины

Кто послужил в качестве модели, так и останется тайной, но искусствоведы считают, что Леонардо допустил некоторые вольности в своем чертеже. Эта работа была не столь портретом, сколько добросовестным изображением идеальных мужских форм с точки зрения математики.

8. Это может быть автопортрет

Поскольку не сохранилось описаний модели, с которой был нарисован данный эскиз, некоторые искусствоведы полагают, что Леонардо рисовал «Витрувианского человека» с себя.

9. У Витрувианского человека была грыжа

Хирург Имперского колледжа Лондона Хутан Ашрафян через 521 лет после создания знаменитого рисунка установил, что у человека, изображенного на эскизе, была паховая грыжа, которая могла привести к его смерти.

10. Чтобы понять полный смысл рисунка, нужно прочесть примечания к нему

Когда эскиз был первоначально обнаружен в записной книжке Лернардо, рядом с ним находились заметки художника относительно пропорций человека, которые гласили: «Архитектор Витрувий утверждает в своей работе по архитектуре, что измерения человеческого тела распределяются согласно следующего принципа: ширина 4 пальцев равна 1 ладони, ступня составляет 4 ладони, локоть составляет 6 ладоней, полный рост человека — 4 локтя или 24 ладони… Эти же измерения Витрувий использовал при строительстве своих зданий».

11. Тело расчерчено мерными линиями

Если внимательно присмотреться к груди, рукам и лицу человека на рисунке, то можно заметить прямые линии, отмечающие пропорции, о которых Леонардо писал в своих заметках. Например, часть лица от низа носа до бровей составляет треть лица, равно как и часть лица от низа носа до подбородка и от бровей до линии, где начинают расти волосы.

12. У эскиза есть и другие, менее эзотерические названия

Эскиз также называют «Канон пропорций» или «Пропорции мужчины».

13. Витрувианский человек одновременно изображает 16 поз

На первый взгляд, можно увидеть только две позы: стоящий человек, который сдвинул ноги и раскинул руки, и стоящий человек с разведенными ногами и поднятыми руками. Но частью гениальности изображения Леонардо является то, что в одном рисунке изображено одновременно 16 поз.

14. Творение Леонардо да Винчи было использовано для отображения проблем современности

Ирландский художник Джон Квигли использовал знаковый образ, чтобы проиллюстрировать проблему глобального потепления. Для этого он изобразил многократно увеличенную копию Витрувианского человека на льдах в Северном ледовитом океане.

15. Оригинал эскиза редко появляется на публике

Копии можно встретить буквально повсеместно, но оригинал слишком хрупкий, чтобы его можно было выставлять на публике.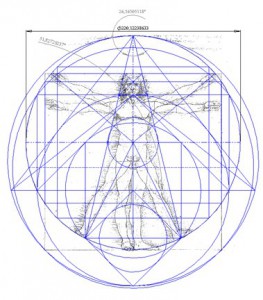 «Витрувианский человек», как правило, хранится под замком в «Галерее Академии» в Венеции.

Золотое сечение в живописи — стр. 2

Золотое сечение в живописи

Переходя к примерам “золотого сечения” в живописи, нельзя не остановить своего внимания на творчестве Леонардо да Винчи. Его личность – одна из загадок истории. Сам Леонардо да Винчи говорил: “Пусть никто, не будучи математиком, не дерзнет читать мои труды”. Он снискал славу непревзойденного художника, великого ученого, гения, предвосхитившего многие изобретения, которые не были осуществлены вплоть до XX в.

Нет сомнений, что Леонардо да Винчи был великим художником, это признавали уже его современники, но его личность и деятельность останутся покрытыми тайной, так как он оставил потомкам не связное изложение своих идей, а лишь многочисленные рукописные наброски, заметки, в которых говорится “обо всем на свете”.

Портрет Монны Лизы (Джоконды) долгие годы привлекает внимание исследователей, которые обнаружили, что композиция рисунка основана на золотых треугольниках, являющихся частями правильного звездчатого пятиугольника. Существует очень много версий об истории этого портрета. Вот одна из них:

Однажды Леонардо да Винчи получил заказ от банкира Франческо де ле Джокондо написать портрет молодой женщины, жены банкира, Монны Лизы. Женщина не была красива, но в ней привлекала простота и естественность облика. Леонардо согласился писать портрет. Его модель была печальной и грустной, но Леонардо рассказал ей сказку, услышав которую, она стала живой и интересной.

Сказка:

Жил-был один бедный человек, было у него четыре сына: три умных, а один из них и так, и сяк. И вот пришла за отцом смерть. Перед тем, как расстаться с жизнью, он позвал к себе детей и сказал: “Сыны мои, скоро я умру. Как только вы схороните меня, заприте хижину и идите на край света добывать себе счастья. Пусть каждый из вас чему-нибудь научится, чтобы мог кормить сам себя”. Отец умер, а сыновья разошлись по свету, договорившись спустя три года вернуться на поляну родной рощи. Пришел первый брат, который научился плотничать, срубил дерево и обтесал его, сделал из него женщину, отошел немного и ждет. Вернулся второй брат, увидел деревянную женщину и, так как он был портной, в одну минуту одел ее: как искусный мастер он сшил для нее красивую шелковую одежду. Третий сын украсил женщину золотом и драгоценными камнями – ведь он был ювелир. Наконец, пришел четвертый брат. Он не умел плотничать и шить, он умел только слушать, что говорит земля, деревья, травы, звери и птицы, знал ход небесных тел и еще умел петь чудесные песни. Он запел песню, от которой заплакали притаившиеся за кустами братья. Песней этой он оживил женщину, она улыбнулась и вздохнула. Братья бросились к ней и каждый кричал одно и то же: “Ты должна быть моей женой”. Но женщина ответила: “Ты меня создал – будь мне отцом. Ты меня одел, а ты украсил – будьте мне братьями.

12.

А ты, что вдохнул в меня душу и научил радоваться жизни, ты один мне нужен на всю жизнь”.

Кончив сказку, Леонардо взглянул на Монну Лизу, ее лицо озарилось светом, глаза сияли. Потом, точно пробудившись от сна, она вздохнула, провела по лицу рукой и без слов пошла на свое место, сложила руки и приняла обычную позу. Но дело было сделано – художник пробудил равнодушную статую; улыбка блаженства, медленно исчезая с ее лица, осталась в уголках рта и трепетала, придавая лицу изумительное, загадочное и чуть лукавое выражение, как у человека, который узнал тайну и, бережно ее храня, не может сдержать торжество. Леонардо молча работал, боясь упустить этот момент, этот луч солнца, осветивший его скучную модель…

Золотое сечение в скульптуре

Скульптурные сооружения, памятники воздвигаются, чтобы увековечить знаменательные события, сохранить в памяти потомков имена прославленных людей, их подвиги и деяния. Известно, что еще в древности основу скульптуры составляла теория пропорций. Отношения частей человеческого тела связывались с формулой золотого сечения.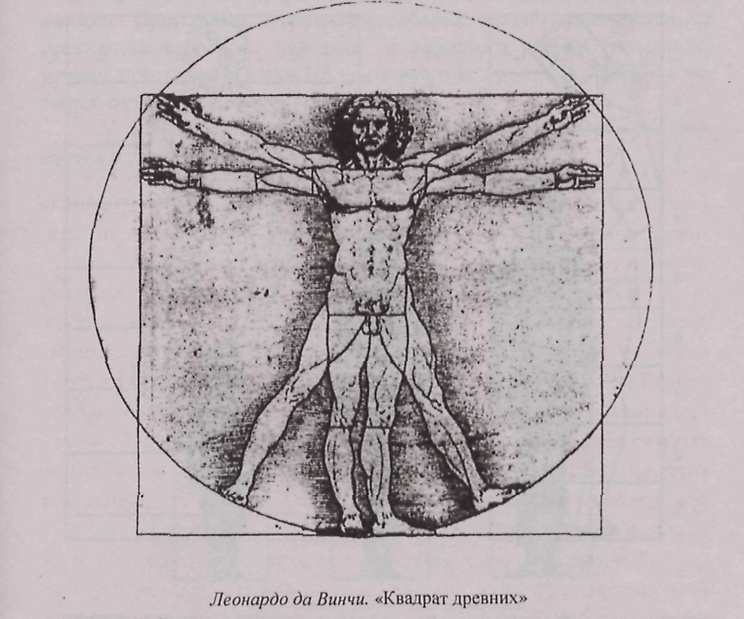 Пропорции “золотого сечения” создают впечатление гармонии красоты, поэтому скульпторы использовали их в своих произведениях. Скульпторы утверждают, что талия делит совершенное человеческое тело в отношении “золотого сечения”. Так, например, знаменитая статуя Аполлона Бельведерского состоит из частей, делящихся по золотым отношениям. Великий древнегреческий скульптор Фидий часто использовал “золотое сечение” в своих произведениях. Самыми знаменитыми из них были статуя Зевса Олимпийского (которая считалась одним из чудес света) и Афины Парфенос.

Золотое сечение в архитектуре

В книгах о “золотом сечении” можно найти замечание о том, что в архитектуре, как и в живописи, все зависит от положения наблюдателя, и что, если некоторые пропорции в здании с одной стороны кажутся образующими “золотое сечение”, то с других точек зрения они будут выглядеть иначе. “Золотое сечение” дает наиболее спокойное соотношение размеров тех или иных длин. Одним из красивейших произведений древнегреческой архитектуры является Парфенон (V в. до н. э.).

Парфенон имеет 8 колонн по коротким сторонам и 17 по длинным, выступы сделаны целиком из квадратов пентилейского мрамора. Благородство материала, из которого построен храм, позволило ограничить применение обычной в греческой архитектуре раскраски, она только подчеркивает детали и образует цветной фон (синий и красный) для скульптуры. Отношение высоты здания к его длине равно 0,618. Если произвести деление Парфенона по “золотому сечению”, то получим те или иные выступы фасада. Другим примером из архитектуры древности является Пантеон.

13.

Заключение

Рациональные и иррациональные числа являются своеобразными противоположностями. Но природа едина, и ее противоположности не только находятся в противодействии, борьбе, но и в единстве. И не удивительно, что многие иррациональные числа выражаются через совокупность целых чисел. Все три числа:p, e и Ф – связаны между собой простыми отношениями и могут быть выражены в виде пределов бесконечных дробей. Кроме того, на примере золотой пропорции показано, что целые числа натурального ряда : 1, 2, 3, … могут быть выражены через иррациональное число Ф. Кроме того, число Ф с любой степенью точности может быть выражено через отношение целых чисел. Разве эти примеры не свидетельствуют о единстве рационального и иррационального в природе?!

Мы так часто говорим о единстве и борьбе противоположностей, что это понятие стало тривиальным, само собой разумеющимся и не требующим исследования. Может быть, поэтому этот фундаментальный закон природы так мало исследован и углублен и, что характерно, почти совершенно не математизирован. А между тем он достоин самого пристального изучения и развития – ведь это один из основных, наиболее общих законов мироздания.

14.

Источники информации

1. Ковалев Ф.В. Золотое сечение в живописи.

К.: Вища школа, 1989.

2. Кеплер И. О шестиугольных снежинках. – М., 1982.

3. Дюрер А. Дневники, письма, трактаты – Л., М., 1957.

4. Цеков-Карандаш Ц. О втором золотом сечении. – София, 1983.

5. Стахов А. Коды золотой пропорции.

6. А.В. Волошинов Пифагор.- М: Просвещение, 1993 г.

7. Г.И. Глейзер История математики в школе VII-VIII кл. Пособие для

учителей.- М: Просвещение, 1982 г.

8. Энциклопедия для детей. Т.11. Математика /Глав. ред. М.Д. Аксенова.

М.: Аванта +, 1999. – 688 с.

9. Леонардо да Винчи: жизнь, творчество, произведения. ИДДК, DISC-0521,

ООО “Бизнессофт”, Россия, 2004.

10.

15.

С давних пор ученые занимались поисками гармонии и совершенства. Одним из таких вопросов был деление отрезка таким образом, чтобы отношение частей было совершенным. Задолго до нашей эры, в различных точках мира, разные ученые, независимо друг от друга, находили это отношение, и у всех это отношение было одним и тем же. И сейчас мы с вами найдем такое деление отрезка, таким способом, каким его нашел знаменитый ученый Пифагор.

I. Построим пятиугольник.

И с помощью пятиугольника мы найдем это совершенное отношение.

Построим две диагонали пятиугольника, как показано на экране

И расставим буквы, как показано на экране. Измерим отрезки АС и ВС и найдем отношение этих отрезков – меньшего к большему. Чему равно это отношение?

— Приближенно 0,6.

А теперь, найдем отношение длин отрезков ВС и АВ. Чему равно это отношение?

— Приближенно 0,6.

Что же получается? Отношение АС к ВС и отношение ВС к АВ приближенно равны 0,6!

— АС:ВС = ВС:АВ=0,6

Такую пропорцию, где меньшее так относится к большему, как большее к целому, назвали золотой пропорцией. А деление отрезка в таком отношении – золотым сечением

Что означает слово сечение?

— Отсечь, рассечь, разделить.

Деление – сечение. А почему его назвали золотым, мы с вами выясним позже.

Проведем остальные диагонали пятиугольника. Какую фигуру мы получили?

— Звезду.

Какая фигура расположена внутри звезды?

— Пятиугольник.

И в этом пятиугольнике можно провести диагонали и получить звезду, и продолжать процесс можно бесконечно!

Этот пятиугольник называется пентаграммой, знак школы Пифагора. Во времена Пифагора он считался магическим. Отношение частей его диагоналей, названное золотым сечением, и приближенно равное 0,6, а более точно 0,618, считалось идеальным.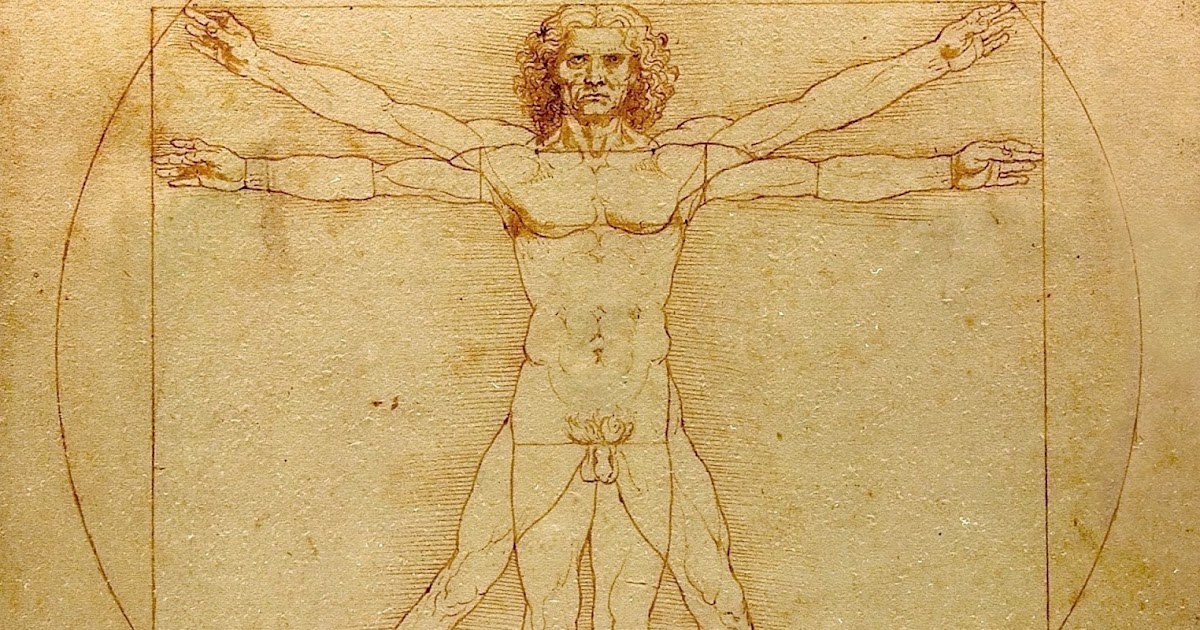 Недаром пятиконечная звезда всегда привлекала человека своей формой.

Вы часто рисовали эту звезду, не задумываясь о ее совершенной форме. А мы с вами обосновали красоту этой фигуры с помощью математики!

II. Существует такое понятие — золотой прямоугольник.

— Отношение ширины прямоугольника к его длине приближенно равно 0,6.

Золотой прямоугольник обладает замечательным свойством: если от золотого прямоугольника отрезать квадрат со стороной равной ширине, то оставшийся прямоугольник также будет золотым.

Психологи утверждают, что человек, живущий в комнате, имеющей форму золотого прямоугольника, более спокойный, уравновешенный.

Итак, мы с вами добрались до первой станции – Живописная.

Перед вами репродукция картины Ивана Шишкина “Корабельная роща”

Назовите самую яркую деталь на этой картине.

— Освещенная солнцем сосна.

Что вы можете сказать о месте расположения этой сосны?

— Она делит картину в отношении золотого сечения.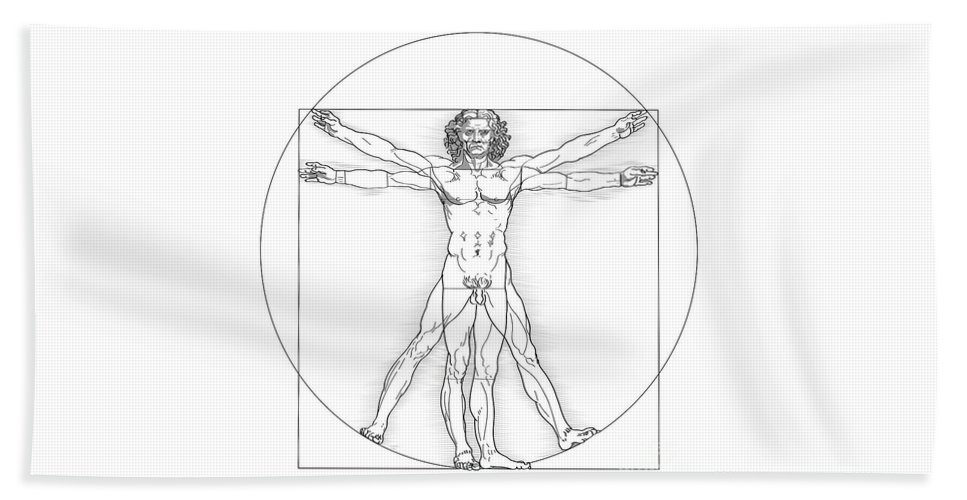

Проверим это!

Ярко освещенная солнцем сосна, стоящая на переднем плане, делит длину картины по горизонтали в золотом отношении.

Справа от сосны, освещенный солнцем пригорок. Он делит по золотому сечению правую часть картины по вертикали. Так же можно найти мотивы золотого сечения и в других частях картины.

Наличие в картине ярких деталей, делящих ее по золотому сечению, придает картине уравновешенность, чувство спокойствия и гармонии.

Картины великих художников, вызывающие непонятную, притягательную силу, запоминающиеся, написаны с применением золотого сечения. Чтобы создать шедевр, даже в искусстве необходима математика!

Следующая станция – Архитектурная

— Перед Вами здание — Парфенон, находится в Греции.

Это здание построено в 5 веке до н.э. зодчим Иктином, в честь богини Афины. Это здание – символ Греции, тоже построено по принципу золотого сечения. Оно считается совершеннейшим из архитектурных сооружений. Отношений высоты здания к его длине равно приближенно 0, 618. По вертикали здание также делится по золотому сечению с точностью до тысячных!!!

Золотое сечение очень часто используется в строительстве, пример тому Дом Пашкова, считавшийся одним из самых красивых зданий в Москве в 19 веке (с него началось развитие библиотеки им. Ленина), Храм Василия Блаженного (Покровский собор) на Красной площади.

Беседуя об архитектуре, мы с вами незаметно добрались до станции – Растительная.

На этой станции мы с вами узнаем о том, что и в природе золотое сечение не редкость. Обратите внимание на цветок.

Кто-нибудь прослеживает мотивы золотого сечения? Листья располагаются на стебле таким образом, что между двумя парами листьев третья расположена в месте золотого сечения. Измерив расстояние от нижнего листа до среднего, затем от среднего до верхнего, найдем отношение этих длин. — Приближенное значение равно 0,6

При таком расположении листьев, как утверждают биологи, достигается максимальное восприятие солнечных лучей.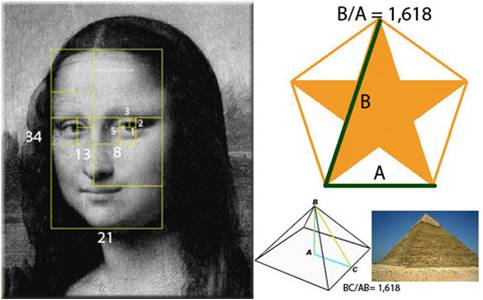 Сама природа определила отношение золотого сечения – человек это заметил и использовал это знание!

Мы добрались до последней станции – Анатомической.

На этой станции мы выясним, почему такое отношение назвали золотым. Перед вами изображение человеческого тела. Что можно сказать о нем?

— Линия пояса делит тело человека в золотом отношении.

А какие части человеческого тела также построены по принципу золотого сечения?

— Лицо, рука, кисть

Золотое сечение повсеместно присутствует в теле человека. И изначально золотое сечение, золотую пропорцию называли божественной пропорцией. Как вы думаете, почему?

— В Библии сказано, что Бог создал человека по образу и подобию своему.

И, когда человек узнал, что его тело делится в таком отношении, он назвал это отношение “божественным”, а Леонардо да Винчи назвал его золотым, в смысле “идеальным”. Золотое сечение дано человеку самой природой в пропорциях своего тела, поэтому золотое сечение стало для человека эталоном красоты.

Когда вы слушаете собеседника, куда вы смотрите?

— В глаза.

А почему не на рот? Как вы думаете?

— Линия глаз делит лицо человека в золотом сечении.

Линия пояса делит тело человека по золотому сечению. Но пропорции тел мужчины и женщины отличаются друг от друга. У одних отношение верхней части тела к нижней более приближенно к значению золотого сечения, как вы думаете, чьи пропорции идеальней – мужчины или женщины? Чье тело более совершенно?

— Женщины

Неправильно! Мужчины. У женщины ноги по отношению к телу короче, чем у мужчины. Но женщины исправили этот несправедливость. Как вы думаете как?

— Каблуки.

Правильно! Женщины носят туфли на каблуках не для того, чтобы увеличить свой рост, а для того, чтобы увеличить, пусть зрительно, длину ног.

А с золотым прямоугольником мы с вами встречаемся в жизни очень часто! Возьмите в руки ваш билет – шоколадку и выясните, является ли она золотым прямоугольником!

— Отношение ширины к длине приближенно равно 0,6.

И лист бумаги, и почтовая открытка, и карманный календарь, и проездной билет, и, как вы убедились, даже шоколадка, являются золотым прямоугольником.

Как вы думаете, почему эти знакомые и привычные для нас вещи выполнены в форме золотого прямоугольника?

— Потому что это приятная для человеческого глаза форма!

А золотое сечение встречается в жизни в самых неожиданных местах. Это и окрас шкуры некоторых животных, и размер ящерицы, и даже куриное яйцо. В старших классах мы узнаем, что золотое сечение присутствует в паутине, в раковине улитке, в расположении семян подсолнуха, и даже в нашей галактике!

Математика вокруг нас. Ее законам подчинена и природа, и деятельность человека, и строение самого человека подчиняется математическим законам.

Секрет Золотого сечения

На протяжении многих веков, для построения гармоничных композиций художники пользуются понятием «Золотого сечения».

«Золотое сечение» — деление отрезка АС на две части таким образом, что большая его часть АВ относится к меньшей ВС так, как весь отрезок АС относится к АВ (т.е. АВ/АС=АС/АВ). Это отношение равно примерно 5:8. «Золотое сечение» — способ pазделить отpезок AB на две неpавные части точкой X так, чтобы выполнялось yсловие AX/XB = XB/AB.На основе данного правила существуют различные способы построения гармоничных композиций.

ЗОЛОТОЕ СЕЧЕНИЕ — пропорция, которой древние маги приписывали особые свойства. Если произвести деление объекта на две неравные части так, что меньшая будет относиться к большей, как большая ко всему объекту, возникнет так называемое золотое сечение. Упрощенно такое соотношение можно представить как 2/3 или 3/5. Замечено, что объекты, содержащие в себе «золотое сечение», воспринимаются людьми как наиболее гармоничные. «Золотое сечение» обнаружено в египетских пирамидах, многих произведениях искусства — скульптурах, картинах, и даже кинофильмах.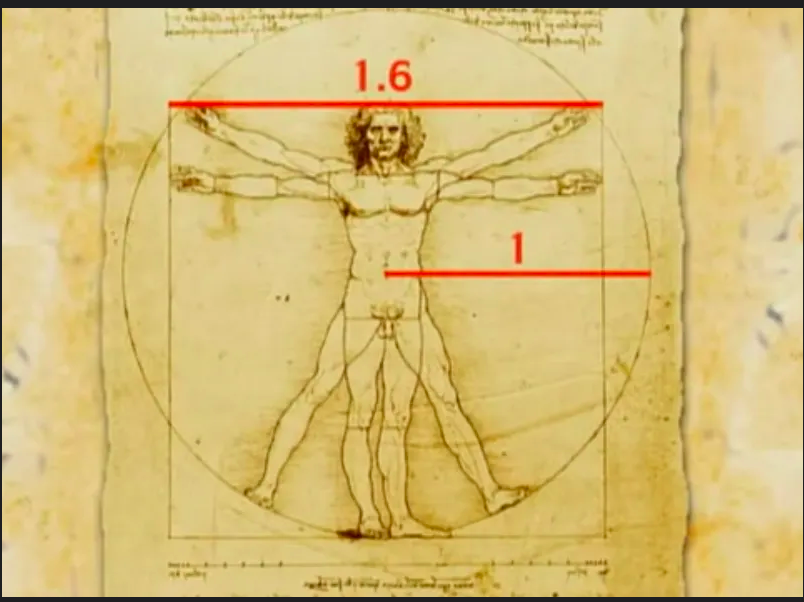 Большинство художников использовали пропорции «золотого сечения» интуитивно. Но некоторые делали это сознательно.

Золотое сечение и гармония

Принято считать, что объекты, содержащие в себе «золотое сечение», воспринимаются людьми как наиболее гармоничные, пропорции пирамиды Хеопса, храмов, барельефов, предметов быта и украшений из гробницы Тутанхамона якобы свидетельствуют, что египетские мастера пользовались соотношениями золотого деления при их создании. Швейцарский архитектор Ле Корбюзье «нашёл», что в рельефе из храма фараона Сети I в Абидосе и в рельефе, изображающем фараона Рамзеса, пропорции фигур соответствуют величинам золотого деления. Зодчий Хесира, изображённый на рельефе деревянной доски из гробницы его имени, держит в руках измерительные инструменты, в которых зафиксированы пропорции золотого деления. В фасаде древнегреческого храма Парфенона присутствуют золотые пропорции. При его раскопках обнаружены циркули, которыми пользовались архитекторы и скульпторы античного мира. В Помпейском циркуле (музей в Неаполе) также заложены пропорции золотого деления, и т. д. и т. п.Ко всем этим утверждениям следует относиться с осторожностью, поскольку во многих случаях это может оказаться результатом подгонки или совпадения.

Золотое сечение и симметрия

Золотое сечение нельзя рассматривать само по себе, отдельно, без связи с симметрией. Великий русский кристаллограф Г.В. Вульф (1863…1925) считал золотое сечение одним из проявлений симметрии. Золотое деление не есть проявление асимметрии, чего-то противоположного симметрии Согласно современным представлениям золотое деление – это асимметричная симметрия. В науку о симметрии вошли такие понятия, как статическая и динамическая симметрия. Статическая симметрия характеризует покой, равновесие, а динамическая – движение, рост. Так, в природе статическая симметрия представлена строением кристаллов, а в искусстве характеризует покой, равновесие и неподвижность. Динамическая симметрия выражает активность, характеризует движение, развитие, ритм, она – свидетельство жизни. Статической симметрии свойственны равные отрезки, равные величины. Динамической симметрии свойственно увеличение отрезков или их уменьшение, и оно выражается в величинах золотого сечения возрастающего или убывающего ряда.

Античный циркуль золотого сечения

В дошедшей до нас античной литературе золотое деление впервые упоминается в «Началах» Евклида. Во 2-й книге «Начал» дается геометрическое построение золотого деления После Евклида исследованием золотого деления занимались Гипсикл (II в. до н.э.), Папп (III в. н.э.) и др. В средневековой Европе с золотым делением познакомились по арабским переводам «Начал» Евклида. Переводчик Дж. Кампано из Наварры (III в.) сделал к переводу комментарии. Секреты золотого деления ревностно оберегались, хранились в строгой тайне. Они были известны только посвященным.

В эпоху Возрождения усиливается интерес к золотому делению среди ученых и художников в связи с его применением как в геометрии, так и в искусстве, особенно в архитектуре Леонардо да Винчи, художник и ученый, видел, что у итальянских художников эмпирический опыт большой, а знаний мало. Он задумал и начал писать книгу по геометрии, но в это время появилась книга монаха Луки Пачоли, и Леонардо оставил свою затею.

Леонардо да Винчи также много внимания уделял изучению золотого деления. Он производил сечения стереометрического тела, образованного правильными пятиугольниками, и каждый раз получал прямоугольники с отношениями сторон в золотом делении. Поэтому он дал этому делению название золотое сечение. Так оно и держится до сих пор как самое популярное.

Великий астроном XVI в. Иоган Кеплер назвал золотое сечение одним из сокровищ геометрии. Он первый обращает внимание на значение золотой пропорции для ботаники (рост растений и их строение).Кеплер называл золотую пропорцию продолжающей саму себя «Устроена она так, – писал он, – что два младших члена этой нескончаемой пропорции в сумме дают третий член, а любые два последних члена, если их сложить, дают следующий член, причем та же пропорция сохраняется до бесконечности».

Построение ряда отрезков золотой пропорции можно производить как в сторону увеличения (возрастающий ряд), так и в сторону уменьшения (нисходящий ряд).

Золотое сечение в греческом искусстве

Идея гармонии, основанной на золотом сечении, не могла не коснуться греческого искусства. Природа, взятая в широком смысле, включала в себя и творческий мир человека, искусство, музыку, где действуют те же законы ритма и гармонии. Предоставим слово Аристотелю: «Природа стремится к противоположностям и из них, а не из подобных вещей, образует созвучие…Она сочетала мужской пол с женским. А не каждый из них с однородным, и таким образом первую общественную связь она образовала через соединение противоположностей, а не посредством подобного. Также и искусство, по-видимому, подражая природе, поступает таким же образом. А именно живопись делает изображения, соответствующие оригиналам, смешивая белые, черные, желтые и красные краски. Музыка создает единую гармонию, смешав в совместном пении различных голосов звуки высокие и низкие, протяжные и короткие. Грамматика из смеси гласных и согласных . .. создала целое искусство».

Взять материал и исключить все лишнее — таков афористически запечатленный план ваятеля, вобравшего в себя всю серьезность философской мудрости античного мыслителя. И это — главная идея греческого искусства, для которого «золотое сечение» впервые стало некоторым эстетическим каноном.

Основу искусства составляет теория пропорций. И, конечно же, вопросы пропорциональности не могли пройти мимо Пифагора. Из философов Греции Пифагор, может быть впервые, старается математически разобрать существо гармонических пропорций. Пифагор знал, что интервалы октавы могут быть выражены числами, которые отвечают соответствующим колебаниям струны, и эти числовые отношения были положены Пифагором в основу их музыкальной гармонии. Пифагору приписывают знание арифметической, геометрической и гармонической пропорций, а также закона золотого сечения. Последнему Пифагор придавал особое, выдающееся значение, сделав пентаграмму или звездчатый пятиугольник отличительным знаком своего «союза».

Платон, заимствуя пифагорейское учение о гармонии, использует пять правильных многогранников («платоновых тел») и подчеркивает их «идеальную» красоту. Значение пропорций Платон подчеркивает в следующем высказывании: «Две части или величины не могут быть удовлетворительно связаны между собой без посредства третьей; наиболее красивым связующим звеном является то, которое совместно с двумя первоначальными величинами дает наиболее совершенное единое целое. Достигается это наилучшим образом пропорцией (аналогией), в которой из трех чисел, плоскостей или тел, среднее так относится ко второму, как первое к среднему, а также второе к среднему как среднее к первому. Из этого следует, что среднее может заменить первое и второе, первое же и второе — среднее и все вместе, таким образом, составляет неразрывное единое целое».

Аристотель основными требованиями красоты выдвигает порядок, пропорциональность и ограниченность в размерах. Порядок возникает тогда, когда между частями целого возникают определенные соотношения, пропорции.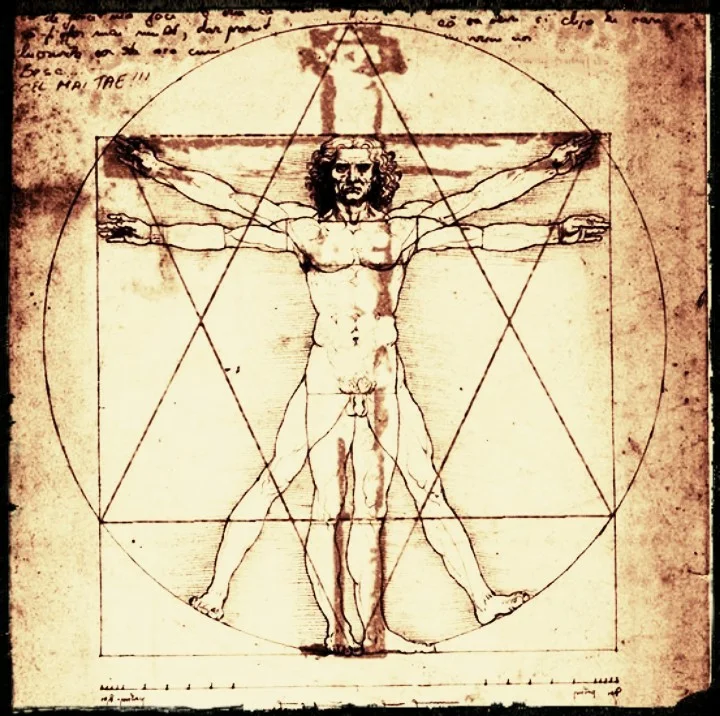 В музыке Аристотель признает октаву наиболее красивым консонансом в виду того, что число колебаний между основным тоном и октавой выражается первыми числами натурального ряда: 1:2. В поэзии, по его мнению, ритмические отношения стиха основаны на малых численных соотношениях, этим самым достигается красивое впечатление. Кроме простоты, основанной на соизмеримости отдельных частей и целого, Аристотель, как и Платон, признает высшую красоту правильных фигур и пропорции, основанной на золотом сечении.

Не только философы Древней Греции, но и многие греческие художники и архитекторы уделяли значительное внимание достижению пропорциональности. И это подтверждается анализом архитектурных сооружений греческих зодчих. Фригийские гробницы и античный Парфенон, «Канон» Поликлета и Афродита Книдская Праксителя, наиболее совершенный греческий театр в Эпидавре и древнейший из дошедших до нас театр Диониса в Афинах — все это яркие образцы ваяния и творчества, исполненные глубокой гармонии на основе золотого сечения.

Театр в Эпидавре построен Поликлетом Младшим в 40-ю Олимпиаду. Рассчитан на 15 тысяч человек. Театрон (место для зрителей) делится на два яруса: первый имеет 34 ряда мест, второй — 21 (числа Фибоначчи!). Раствор угла, объемлющего пространство между театроном и скеной (пристройка для переодевания актеров и хранения реквизита), делит окружность основания амфитеатра в отношении 137,5:222,5 = 0.618 (золотая пропорция). Это соотношение реализовано практически во всех античных театрах. Данная пропорция у Витрувия в его схематических изображениях такого рода построек, составляет 5:8, то есть рассматривается как отношение чисел Фибоначчи.

Театр Диониса в Афинах трехъярусный. Первый ярус имеет 13 секторов, второй -21 (числа Фибоначчи!). Отношение растворов углов, делящих окружность основания на две части — то же самое, то есть золотая пропорция.

Три смежных числа из начального фрагмента ряда Фибоначчи 5, 8, 13 есть величины разностей между радиусами окружностей, лежащих в основании плана построения большинства театров. Ряд Фибоначчи служил как бы масштабной шкалой, где каждое число соответствует целым единицам аттического фута, но в то же время эти величины связаны между собой единой математической закономерностью.

При построении храмов за основу брался человек как «мера всех вещей»: в храм он должен входить «с гордо поднятой головой». Его рост делился на 6 единиц (греческих футов), которые откладывались на линейке, а на нее наносилась шкала, жестко связанная с последовательностью шести членов ряда Фибоначчи: 1, 2, 3, 5, 8, 13 (их сумма равна 32 = 25). Прибавлением или вычитанием этих эталонных отрезков достигались необходимые пропорции сооружения. Шестикратное увеличение всех отложенных на линейке размеров сохраняло гармоническую пропорцию. В соответствии с этой шкалой и строили храмы, театры или стадионы.

Что касается греческой скульптуры, то и здесь искания пропорциональности человеческого тела — несомненны. Еще Диодор упоминает о двух скульпторах с острова Самос — о Телекле и Теодоре, которые якобы впервые перенесли выработанные в Египте нормы человеческого тела в греческую скульптуру.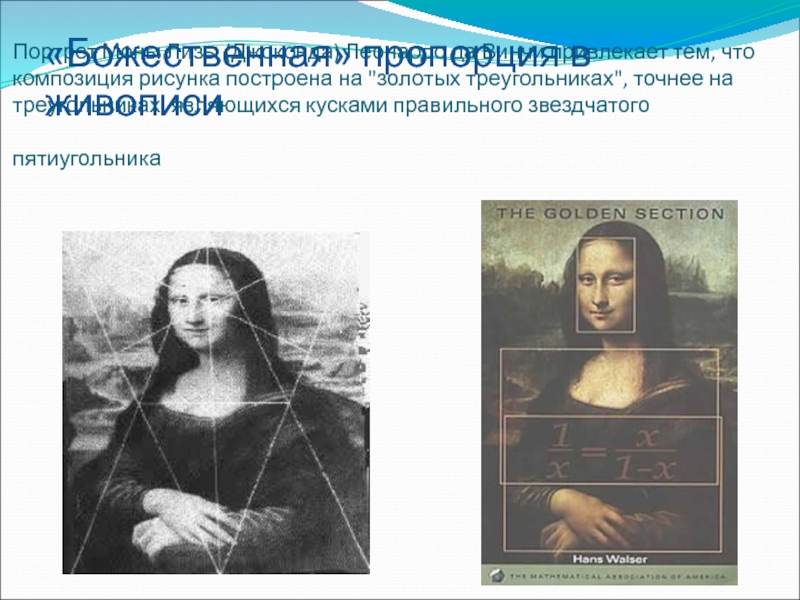 Плиний свидетельствует, что скульптор Поликлет написал статью о правильных пропорциях человеческого тела и вылепил знаменитую статую Дорифора (Рис. 1), которая долгое время служила каноном.

Рис. 1

Гармонический анализ статуи Дорифора, изложенный в книге русского Проф. Г.Д. Гримма «Пропорциональность в архитектуре» (1933), указывает на следующую связь знаменитой статуи с золотым сечением M = t:

первый раздел фигуры Дорифора или ее полной высоты M0 = 1 в пропорции золотого сечения M1 = t -1 и M2 = t -2 проходит через пупок;

второй раздел нижней части туловища M1 = t -1 и M2 = t -2 проходит M2 = t -2 и M3 = t -3 проходит через линию колена;

третий раздел M3 = t -3 и M4 = t -4 проходит через линию шеи.

Теория измерения гармонии по принципу деления целого в среднем и крайнем отношении («золотое сечение»), разработанная античными математиками, и стала тем фундаментом, той стартовой площадкой, на которой впоследствии были воздвигнуты концепции гармонии в науке и искусстве новоевропейской науки.

Золотое сечение в живописи

Переходя к примерам “золотого сечения” в живописи, нельзя не остановить своего внимания на творчестве Леонардо да Винчи. Его личность – одна из загадок истории. Сам Леонардо да Винчи говорил: “Пусть никто, не будучи математиком, не дерзнет читать мои труды”. Он снискал славу непревзойденного художника, великого ученого, гения, предвосхитившего многие изобретения, которые не были осуществлены вплоть до XX в.

Нет сомнений, что Леонардо да Винчи был великим художником, это признавали уже его современники, но его личность и деятельность останутся покрытыми тайной, так как он оставил потомкам не связное изложение своих идей, а лишь многочисленные рукописные наброски, заметки, в которых говорится “обо всем на свете”.

Портрет Монны Лизы (Джоконды) долгие годы привлекает внимание исследователей, которые обнаружили, что композиция рисунка основана на золотых треугольниках, являющихся частями правильного звездчатого пятиугольника. Существует очень много версий об истории этого портрета. Вот одна из них:

Однажды Леонардо да Винчи получил заказ от банкира Франческо де ле Джокондо написать портрет молодой женщины, жены банкира, Монны Лизы. Женщина не была красива, но в ней привлекала простота и естественность облика. Леонардо согласился писать портрет. Его модель была печальной и грустной, но Леонардо рассказал ей сказку, услышав которую, она стала живой и интересной.

Сказка:

Жил-был один бедный человек, было у него четыре сына: три умных, а один из них и так, и сяк. И вот пришла за отцом смерть. Перед тем, как расстаться с жизнью, он позвал к себе детей и сказал: “Сыны мои, скоро я умру. Как только вы схороните меня, заприте хижину и идите на край света добывать себе счастья. Пусть каждый из вас чему-нибудь научится, чтобы мог кормить сам себя”. Отец умер, а сыновья разошлись по свету, договорившись спустя три года вернуться на поляну родной рощи. Пришел первый брат, который научился плотничать, срубил дерево и обтесал его, сделал из него женщину, отошел немного и ждет. Вернулся второй брат, увидел деревянную женщину и, так как он был портной, в одну минуту одел ее: как искусный мастер он сшил для нее красивую шелковую одежду. Третий сын украсил женщину золотом и драгоценными камнями – ведь он был ювелир. Наконец, пришел четвертый брат. Он не умел плотничать и шить, он умел только слушать, что говорит земля, деревья, травы, звери и птицы, знал ход небесных тел и еще умел петь чудесные песни. Он запел песню, от которой заплакали притаившиеся за кустами братья. Песней этой он оживил женщину, она улыбнулась и вздохнула. Братья бросились к ней и каждый кричал одно и то же: “Ты должна быть моей женой”. Но женщина ответила: “Ты меня создал – будь мне отцом. Ты меня одел, а ты украсил – будьте мне братьями.

А ты, что вдохнул в меня душу и научил радоваться жизни, ты один мне нужен на всю жизнь”.

Кончив сказку, Леонардо взглянул на Монну Лизу, ее лицо озарилось светом, глаза сияли. Потом, точно пробудившись от сна, она вздохнула, провела по лицу рукой и без слов пошла на свое место, сложила руки и приняла обычную позу. Но дело было сделано – художник пробудил равнодушную статую; улыбка блаженства, медленно исчезая с ее лица, осталась в уголках рта и трепетала, придавая лицу изумительное, загадочное и чуть лукавое выражение, как у человека, который узнал тайну и, бережно ее храня, не может сдержать торжество. Леонардо молча работал, боясь упустить этот момент, этот луч солнца, осветивший его скучную модель…

Золотое сечение в скульптуре

Скульптурные сооружения, памятники воздвигаются, чтобы увековечить знаменательные события, сохранить в памяти потомков имена прославленных людей, их подвиги и деяния. Известно, что еще в древности основу скульптуры составляла теория пропорций. Отношения частей человеческого тела связывались с формулой золотого сечения. Пропорции “золотого сечения” создают впечатление гармонии красоты, поэтому скульпторы использовали их в своих произведениях. Скульпторы утверждают, что талия делит совершенное человеческое тело в отношении “золотого сечения”. Так, например, знаменитая статуя Аполлона Бельведерского состоит из частей, делящихся по золотым отношениям. Великий древнегреческий скульптор Фидий часто использовал “золотое сечение” в своих произведениях. Самыми знаменитыми из них были статуя Зевса Олимпийского (которая считалась одним из чудес света) и Афины Парфенос.

Золотое сечение в архитектуре

В книгах о “золотом сечении” можно найти замечание о том, что в архитектуре, как и в живописи, все зависит от положения наблюдателя, и что, если некоторые пропорции в здании с одной стороны кажутся образующими “золотое сечение”, то с других точек зрения они будут выглядеть иначе. “Золотое сечение” дает наиболее спокойное соотношение размеров тех или иных длин. Одним из красивейших произведений древнегреческой архитектуры является Парфенон (V в. до н. э.).

Парфенон имеет 8 колонн по коротким сторонам и 17 по длинным, выступы сделаны целиком из квадратов пентилейского мрамора. Благородство материала, из которого построен храм, позволило ограничить применение обычной в греческой архитектуре раскраски, она только подчеркивает детали и образует цветной фон (синий и красный) для скульптуры. Отношение высоты здания к его длине равно 0,618. Если произвести деление Парфенона по “золотому сечению”, то получим те или иные выступы фасада. Другим примером из архитектуры древности является Пантеон.

Заключение

Рациональные и иррациональные числа являются своеобразными противоположностями. Но природа едина, и ее противоположности не только находятся в противодействии, борьбе, но и в единстве. И не удивительно, что многие иррациональные числа выражаются через совокупность целых чисел. Все три числа:p, e и Ф – связаны между собой простыми отношениями и могут быть выражены в виде пределов бесконечных дробей. Кроме того, на примере золотой пропорции показано, что целые числа натурального ряда : 1, 2, 3, … могут быть выражены через иррациональное число Ф. Кроме того, число Ф с любой степенью точности может быть выражено через отношение целых чисел. Разве эти примеры не свидетельствуют о единстве рационального и иррационального в природе?!

Мы так часто говорим о единстве и борьбе противоположностей, что это понятие стало тривиальным, само собой разумеющимся и не требующим исследования. Может быть, поэтому этот фундаментальный закон природы так мало исследован и углублен и, что характерно, почти совершенно не математизирован. А между тем он достоин самого пристального изучения и развития – ведь это один из основных, наиболее общих законов мироздания.

Источники информации

10. А.В. Волошинов Пифагор.- М: Просвещение, 1993 г.

11. Г.И. Глейзер История математики в школе VII-VIII кл. Пособие для учителей.- М: Просвещение, 1982 г.

12. Энциклопедия для детей. Т.11. Математика /Глав. ред. М.Д. Аксенова. – М.: Аванта +, 1999. – 688 с.

13. Леонардо да Винчи: жизнь, творчество, произведения. ИДДК, DISC-0521, ООО “Бизнессофт”, Россия, 2004.

15. Ковалев Ф.В. Золотое сечение в живописи. К.: Вища школа, 1989.

16. Кеплер И. О шестиугольных снежинках. – М., 1982.

17. Дюрер А. Дневники, письма, трактаты – Л., М., 1957.

18. Цеков-Карандаш Ц. О втором золотом сечении. – София, 1983.

19. Стахов А. Коды золотой пропорции.

Веб-дизайн как у Да Винчи. Оформляем сайт с помощью золотого сечения

21 мая 2021 г.

Время чтения: 4 минуты

У больших компаний есть свой секрет создания идеального логотипа и красивого дизайна сайта. Некоторые знакомые нам страницы и логотипы известных брендов выверены с помощью правила золотого сечения. Эта сугубо математическое явление помогает вычислить гармоничные размеры любого объекта и сделать его приятным глазу.

Золотое сечение — это фиксированная пропорция. Чтобы её получить, нужно разделить прямой отрезок произвольной длины с учётом следующего условия: длинная часть отрезка относится к короткой так же, как весь отрезок относится к длинной части. Эта пропорция всегда равна 1,618 и у этого числа есть собственное название, «фи».

Это значение было известно ещё в Древнем Египте и существует теория, что его использовали при сооружении пирамид. А наиболее широкую популярность метод золотого сечения приобрёл в Средние века. По мнению исследователей, композиция величайшего шедевра живописи «Мона Лиза» авторства Леонардо да Винчи была построена именно с использованием числа «фи».

Рассмотрим, каким образом золотое сечение применяется в дизайне. На основе отрезка, разделённого на две части в пропорции 1 к 1,618, построим квадрат и прямоугольник.

В результате мы получим прямоугольник с золотым сечением, который также называют золотым. Правая его часть тоже представляет собой золотой прямоугольник. Если выделить в нём квадрат, то оставшаяся часть снова окажется прямоугольником с золотым сечением — и так до бесконечности.

Если плавной линией соединить по два противоположных угла каждого из квадратов, то мы получим идеальную спираль, созданную по правилу золотого сечения.

Чтобы получить несколько кругов, которые относятся друг к другу в соотношении 1 к 1,1618, тоже воспользуемся квадратами.

Полученные элементы можно применять в проектировании макетов страниц и логотипов.

Разделение макета на зоны

Чтобы провести границы между блоками на будущей веб-странице, используйте число «фи». Самое простое решение — разделить область страницы на две части по вертикали так, чтобы значения ширины получившихся прямоугольников имели то самое соотношение 1 к 1,618.

Например, если нам необходимо разделить область шириной 1080 пикселей, то делим 1080 на число «фи» и получаем 668 пикселей — ширину большего прямоугольника. Осталось вычесть это значение из общей ширины и получить ширину меньшего прямоугольника. Теперь можно приступать к наполнению макета.

Известный пример использования золотого сечения в веб-дизайне — сайт журнала National Geographic.

Регулирование «воздуха»

Профессиональные дизайнеры знают, что правильно расставить акценты в изображении помогает свободное пространство вокруг его элементов. Чтобы понять, сколько «воздуха» необходимо рядом с каждым из элементов, наложите на макет один или несколько золотых прямоугольников. Для этого можно использовать такой шаблон.

К слову, готовые шаблоны с прямоугольниками, кругами и спиралью можно скачать, например, здесь или здесь.

Если вы расположите элементы по углам и краям квадратов, то свободного пространства между ними будет именно столько, сколько необходимо. Афиша фестиваля Bregenzer Festspiele была оформлена именно по этому принципу.

Направление взгляда пользователя

Чтобы расположить элементы в нужном порядке, необязательно размещать их строго сверху вниз или справа налево. Золотая спираль, построенная по углам квадратов золотого прямоугольника, поможет выстроить нестандартную траекторию движения глаз пользователей по странице.

Привяжите элементы к разным участкам спирали: начните повествование в её самой длинной части, а завершите рассказ в её центре. Дизайнер Тим Роузиль при оформлении своего персонального сайта поступил именно так.

Создание логотипов

Здесь мы вспомним об окружностях, вписанных в квадраты золотого прямоугольника. Их можно использовать в разработке аккуратных логотипов. Располагайте произвольным образом внутри большого круга круги поменьше и формируйте ту фигуру, которая вам необходима. Логотип Pepsi — один из ярких примеров использования кругов с золотым сечением.

Выбор размера текста

И ещё один полезный совет по использованию золотого сечения. На страницах мы используем фрагменты текста с разным кеглем. Чтобы подобрать оптимальные размеры шрифта для заголовков, подзаголовков и основного текста, также потребуется число «фи». К примеру, разделите выбранный вами размер заголовка на 1,618 и вы получите подходящий размер для подзаголовков.

Кстати, для вычисления «золотых» величин можно воспользоваться онлайн-калькуляторами Phiculator и Golden Ratio Calculator.

Подведём итоги и кратко опишем полезные свойства золотого сечения в веб-дизайне. Оно позволяет:

• структурировать контент на странице,
• сбалансированно располагать элементы,
• облегчать восприятие информации и взаимодействие со страницей,
• создавать гармоничные логотипы,
• вызывать позитивные эмоции у пользователей.

Код да Винчи и ряды Фибоначчи

Введение

Глава 1

Золотое сечение, или Код да Винчи

1.1. Что такое код да Винчи?

1.2. Геометрическое определение Золотого сечения

1.3. Алгебраические свойства золотой пропорции

1.4. Уравнение золотой пропорции

1.5. Золотой прямоугольник

1.6. Декагон: связь Золотого сечения с числом p

1.7. Золотой прямоугольный треугольник и золотой эллипс

1.8. Пентагон и золотой равнобедренный треугольник

1.9. Золотое сечение и тайны египетской культуры

1.10. Золотое сечение в греческой культуре

1.11. Золотое сечение в искусстве Возрождения. “Мона Лиза” Леонардо да Винчи

1.12. “Божественная пропорция” Луки Пачоли

1.13. “Пропорциональность в архитектуре” Г. Д. Гримма

1.14. Золотое сечение в искусстве XIX и XX веков

1.15. Формула красоты

1.16. Золотое сечение в музыке

1.17. Обобщенные золотые пропорции

1.18. Обобщенный принцип Золотого сечения и закон структурной гармонии систем

Глава 2

Ряды Фибоначчи

2.1. Кто такой Фибоначчи?

2.2. Числа Фибоначчи

2.3. Вариации на тему Фибоначчи

2.4. Числа Люка

2.5. Формула Кассини

2.6. Теорема Пифагора и числа Фибоначчи

2.7. Формулы Бине

2.8. Гиперболические функции Фибоначчи и Люка

2.9. Золотой шофар и геометрия Вселенной

2.10. Прямоугольник Фибоначчи и спираль Фибоначчи

2.11. Химия по Фибоначчи

2.12. Симметрия природы и природа симметрии

2.13. Вездесущий филлотаксис

2.14. “Фибоначчиевы” резонансы генетического кода

2.15. Музыка стихов

2.16. Проблема выбора, или Умрет ли буриданов осел?

2.17. Волны Эллиотта

2.18. Обобщенные числа Фибоначчи и математика гармонии

Глава 3

Правильные многогранники

3.1. Код да Винчи в платоновых телах

3.2. Архимедовы тела

3.3. Тайна египетского календаря

3.4. Додекаэдро-икосаэдрическая доктрина

3.5. Иоганн Кеплер: от “Мистерии” до “Гармонии”

3.6. Резонансная теория Солнечной системы

3.7. Икосаэдр как главный геометрический объект математики

3.8. Правильные многогранники в природе и современной науке

3.9. Использование правильных многогранников в искусстве

3.10. Нужно ли вводить Золотое сечение в школьное образование?

Леонардо и математика — Фонд Моны Лизы

Важное отношение математики к искусству невозможно недооценить, обсуждая более поздние работы Леонардо, и в многочисленных документах, письмах и заметках важность этого хорошо задокументирована. Иногда кажется, что он одержим этими проблемами: например, во время работы над «Моной Лизой» Фра да Новеллара сообщает, что Леонардо сильно сосредоточился на геометрии.

“

Non mi legga chi non e matematico. ”

«

Пусть меня никто не читает, если я не математик. ”

Леонардо да Винчи

Конечно, наставление Луки Пачоли в Милане было откровением для Леонардо, и это особенно проявилось в « Тайной вечере ». В математике существует уникальное число 0,618, которое является единственным, когда деление на единицу (1,0) дает обратную величину — 1,618. Это называется «золотым сечением»: также известно как «золотое правило», «золотая огранка», «золотое число», «золотая пропорция», «золотое сечение».Формула была впервые записана Евклидом, ок. 300 г. до н. Э. В пятом атрибуте Бога, функциональном сравнении, Пачоли устанавливает «Божественную пропорцию» по отношению к квинтэссенции Платона.

«Портрет фра Луки Бартоломео де Пачоли» , Якопо де Барбари, около 1495 г. (атрибуция не подтверждена). Стол заполнен геометрическими инструментами: грифелем, мелом, циркулем, моделью додекаэдра. К потолку подвешен ромбокубооктаэдр, наполовину заполненный водой. Пачоли демонстрирует теорему Евклида.

Буква «A», иллюстрация и дизайн, для модели De Divina Proportione Луки Пачоли.

« Как Бог наделяет бытие небесной добродетелью, называемой другим именем« пятая сущность », а через это одно — четырем другим простым телам, то есть четырем земным элементам… и через них всем остальным. в природе.Таким образом, эта наша пропорция является формальным существом (согласно Тимею) неба, приписывая ему фигуру твердого тела, называемого Додекаэдром, также известного как твердое тело из двенадцати пятиугольников. ”Лука Пачоли, De Divina Proportione

Почему это важно? Для Леонардо и других мастеров эпохи Возрождения «золотое сечение» стало важным инструментом в вопросе точной пропорциональности. Фра Лука излагает теорию в 1498 году, преподавая в Милане, а позже, в 1509 году, он и Леонардо вместе опубликовали De Divina Proportione , на котором изображен один из самых известных рисунков, связанных с Леонардо: «Человек пропорции ». », также известный как« Витрувианский человек », который стал одним из самых знаковых изображений в мире.Тем временем, когда французы, наконец, снова оккупируют Милан в 1500 году, они берут из круга Леонардо феррарского архитектора Джакомо Андреа, который интерпретировал и перевел некоторые работы Витрувия для Леонардо, а затем публично обезглавил и расквартировал его в мае. 12, заставляя замолчать жизненно важный голос науки и независимую мысль. Это послание не потеряно для Леонардо, который не теряет времени на то, чтобы изменить свою лояльность французам. В то же время можно почувствовать, как Леонардо маскирует свои собственные новые знания в технике живописи, которые проявляются в его более поздних работах.

Когда фра Пьетро да Новеллара и другие пишут Изабелле д’Эсте в первые годы XVI века, есть важные упоминания о том, что Леонардо не имеет терпения рисовать из-за его постоянных занятий геометрией. Когда Леонардо вернулся во Флоренцию в 1500 году, он сделал это в компании своего учителя математики фра Луки Пачоли, и с образовательной точки зрения эту связь нельзя недооценивать. Хотя сам Леонардо в общих чертах пишет о важности математики, маловероятно, что это относится к дисциплинам алгебры, тригонометрии и исчисления, которые распространены в современных классах.Скорее, его больше всего интересует геометрия, которая имеет самое непосредственное отношение к его искусству. Леонардо видит в геометрии точность, с помощью которой он может создавать уникальные композиции в идеальной гармонии в ее окружении. Две версии Моны Лизы пронизаны математическим сходством, а также божественной пропорцией.

Сразу после публикации De Divina Proportione Рафаэль написал в Ватикане свою массивную и необычную фреску « Афинская школа ». Это включает в себя многие математические теории Луки и Леонардо; Кроме того, представлено большинство исторически известных персонажей Древней Греции.Это также дань уважения мастеру. Сам Рафаэль — это Апеллес, великий художник; Браманте, архитектор базилики Святого Петра, — это Евклид; и идеально сосредоточен в работе Платона в представлении Леонардо.

Кеннет Кларк пишет: « Если бы человек был мерой всех вещей, физически совершенный человек, несомненно, был бы мерой всей красоты, и его пропорция должна быть каким-то образом сведена к математическим терминам и соответствовать этим абстрактным совершенствам, квадрату, круг, и золотое сечение .Кларк продолжает напоминать нам, что « Этот союз искусства и математики далек от нашего собственного мышления, но он был фундаментальным для Возрождения. Это было основой перспективы », т.е.« научного представления удаляющихся фигур в пространстве … »

Леонардо никогда не уставал от тесной взаимосвязи между искусством и визуальной математикой. Его увлечение чувством бесконечности, как показано в его узлах, было, возможно, также невольным предшественником теорий фрактальной геометрии и их взаимосвязи, в свою очередь, с природой.Хотя эти математические теории были уточнены только в 1980-х годах, Леонардо работал над их практическим применением 500 лет назад.

Прекрасный пример — замысловатый и тонкий узор на блузке Моны Лизы. Дизайн может поначалу показаться безобидным, но мозг, который его задумал, и гений, создавший его, были посвящены вере в то, что глубокое понимание математики было основополагающим для создания великого искусства. Одна из вещей, которая делает «Мона Лизу ранее » такой выдающейся работой, заключается в том, что она не только отображает полный спектр знаний о геометрии, часто используемых Леонардо, но и то, что эти новаторские элементы можно увидеть на всей картине.

«

ЗОЛОТОЕ СООТНОШЕНИЕ » В ИСКУССТВЕ

Истинная золотая спираль: длина стороны большего квадрата до следующего меньшего квадрата находится в «золотом сечении».

Во многих книгах утверждается, что если вокруг Лувра нарисовать прямоугольник « Мона Лиза », отношение высоты к ширине этого прямоугольника равно «золотому сечению». Не существует документации, указывающей на то, что Леонардо сознательно использовал «золотое сечение» в композиции Лувра « Мона Лиза », а также на то, где именно должен быть нарисован прямоугольник.Тем не менее, необходимо признать тот факт, что Леонардо был близким другом Луки Пачоли, опубликовавшего в 1509 году трехтомный трактат о «золотом сечении» под названием De Divina Proportione ( On Divine Proportione ). Иллюстрации многогранников Леонардо для этой публикации и его взгляды на то, что некоторые пропорции тела демонстрируют «золотое сечение», привели некоторых ученых к предположению, что он включил «золотое сечение» в (некоторые) свои картины.

Ученые много писали о мнении, что Леонардо строил свои портреты на основе треугольной конструкции, следовательно, подразумевая, что эта идея была нововведением Леонардо; то, что делало его работы уникальными.На самом деле человеческое тело, позирующее портрету, естественно принимает треугольную форму. Кроме того, количество градусов в критическом угле любого треугольника также может быть произвольным. Нет жесткого правила.

В случае « Early Mona Lisa », ноги (синего) треугольника показаны правильно размещенными в нижних углах, а вершина делит ширину картины пополам вверху. Теперь применяется диаграмма «золотого сечения».Он прижимается к краю левой колонны и, проходя через макушку ее головы, точно встречается с ножкой треугольника. В то же время спираль красиво обрамляет ее лицо, при этом закругленная сторона справа, а вертикальная — слева. Кроме того, спираль извивается от кончика ее носа, касаясь нижней части ее подбородка, и полностью направляется к ее правой руке, от локтя до большого пальца.

Тот же набор диаграмм был нанесен на Лувр « Мона Лиза ». Теоретически, если Леонардо нарисовал или спроектировал обе картины, то применение диаграмм должно одинаково хорошо работать на обеих.Как известно, деревянная панель Лувра « Мона Лиза » несколько меньше холста на более ранней картине, и, что усложняет ситуацию, фигура Лувра « Мона Лиза » немного больше, чем на картине. «, ранее Мона Лиза ». Теории как треугольной конструкции, так и «золотого сечения», изображенного на диаграмме, работают одинаково хорошо.

Однако из-за размера этого изображения некоторые края и начальные точки диаграммы находятся за пределами плоскости панели.Это не является проблемой. При масштабировании чертежей не все уравнения должны быть на одной странице. Часто точки схода и линии горизонта не видны зрителю на картине; но это не значит, что их там нет. Конструкция сооружения должна соответствовать ограничениям, налагаемым размером и формой опоры. Сначала это может показаться ограничительным; но квалифицированный чертежник сможет применить важную информацию, более или менее так, как показано здесь.

Вертикальная красная пунктирная линия — произвольное добавление.В случае обоих портретов он продолжает вертикальную линию, начинающуюся от нижней точки подбородка, и идеально разделяет лицо пополам до линии пробора.

Геометрия красоты в картинах Леонардо да Винчи

Альфонсо Рубино

Работы Леонардо соединены между собой невидимой геометрически-гармоничной тканью. Открытие было сделано путем изучения рисунка « Витрувианский человек ». Леонардо придает первостепенное значение внешним размерам картин, предлагая нам рассмотреть не только содержание, но и поддержку его работ.Под опорой я подразумеваю внешние размеры работы. В случае с Витрувианским человеком простыня, согласно моей гипотезе, изначально имела высоту 34,52 см и ширину 24,66 см.

Историки искусства, следуя традиции Витрувия, определяют возможное присутствие геометрической ткани на основе произведения искусства: иконограммы.

В работах Леонардо инконограммы связаны друг с другом как типологически, так и размерно. Геологическое семя, которое их производит, — это геометрическая модель, обнаруженная у Витрувианского человека.

Это гармоничный универсальный код, основанный на квадратуре Архимеда 22/7.

Витрувианский человек

Гармонический код Витрувианского Человека, несомненно, можно найти и в других его важных работах:

« Благовещение », « Дева в скалах » в Лувре, « Крещение Христа » и « Тайная вечеря ».

А в работе Леонардо можно восстановить последовательность иконограмм в зависимости от уровня сложности.

1. Благовещение — уровень 1
2. Крещение Христа — уровень 2
3. Мадонна в скалах, Лувр — уровень 3
4. Витрувианский лист — Уровень 1
5. Витрувианский человек — уровень 3
6. Более ранняя Мона Лиза — уровень 2
7. Лувр Мона Лиза — уровень 3b

Анализ « Крещения Христа » Верроккьо (нарисованного с помощью Леонардо) позволяет понять, что код был передан Леонардо Его Учителями.Он был не единственным художником, который использовал его в то время. Например, код можно найти « Spring » Боттичелли.

В этом документе вы найдете геометрическую последовательность между « Витрувианский человек », Лувром и более ранней Мона Лизой. Он логический и дедуктивный порядок.

Ткань с геометрической гармонией предполагает, что автор « Early Mona Lisa » совпадает с автором версии Лувра. Учитывая представленные геометрические данные, казалось бы невозможным, чтобы более ранняя версия могла быть выполнена любым художником, кроме Леонардо.

Геометрическая конструкция для создания круга / квадрата человеческой фигуры.

По ссылке ниже вы найдете сравнительную таблицу с различными иконографическими моделями Леонардо
http://alfonsorubino.altervista.org/

В таблице ниже вы найдете как теоретические, так и эффективные размеры работ Леонардо. (Теоретические размеры опоры « Витрувианский человек » зафиксированы заранее).

	Фактический			Теоретическая
Благовещение	98	217		97,81	216,47
Крещение Христа	151	177		152,04	177,37
‘ Дева в скалах ‘	122	199		122,26	199,13
Витрувианский человек	34,4	24,5		34,52	24,66
Лувр Мона Лиза	53	76,8		53,14	76,77
Ранее Мона Лиза	64	86		64,11	85,51

По приведенной ниже ссылке вы найдете сравнительную таблицу между Лувром « Мона Лиза » и « Раннее Мона Лиза »
http: // alfonsorubino.altervista.org/
Библиография по теме автора:
a- La Triplice Cinta –Roberto Mosca & Alfonso Rubino
La geometria della bellezza nelle opere dei maestri di ogni tempo-Terra Nuova Edizioni — Firenze
b- ‘Uomo Vitruviano di Leonardo –libro elettronico
Casa Editrice — Liberfaber — Principato di Monaco
http://www.liberfaber.com/

Слайд-шоу основных элементов доступно здесь:
http: // www.slideshare.net/alfonsorubino/dall-uomo-vitruviano-alle-donne-vitruviane-di-leonardo2

Леонардо да Винчи Математика

Это тот, для кого математика очень важна в его работах. К ним относятся такие произведения, как «Тайная вечеря», «Витрувианский человек» и «Поклонение волхвов» и многие другие.

Однако именно в книге Дэна Брауна «Код да Винчи» многие сталкивались с идеями да Винчи о математике и искусстве.

Математика и искусство

Когда дело доходит до математики, она имеет давнюю связь с искусством. Считается, что математические идеи, такие как линейная перспектива, симметрия, золотое сечение и геометрические формы, имеют прямое влияние на искусство. Такие идеи могут формировать наш взгляд на вещи, поскольку они улучшали работу. Именно в период Возрождения и таких художников, как Леонардо да Винчи, идеи о математике в искусстве привлекли внимание.

Знания Леонардо да Винчи в математике начали развиваться только после того, как ему исполнилось сорок. Большая часть его образования была получена благодаря получению знаний в ходе постоянной программы самообучения. Когда ему было за сорок, он изучал математику у францисканского монаха по имени Лукка Пачоли. После этого да Винчи использовал то, что он узнал, изучая инженерию и анатомию.

Золотое сечение / Божественная пропорция

В искусстве золотое сечение — широко известное понятие в математике.Это особое число, которое существует со времен египтян и греков. Это особенное число, потому что это иррациональное число. Золотой паек, известный как фи, имеет ценность около 1,618. На протяжении многих лет золотое сечение было известно под многими именами — Золотая середина, Золотое сечение и божественная пропорция среди многих других. Золотая пайка проявляется не только в природе и науке, но и в искусстве. Его связь с искусством возникла в конце 1400-х годов от Леонардо да Винчи и францисканского монаха по имени Лукка Пачоли.

Пачоли был математиком, написавшим книгу «De divina пропорционально» (Божественная пропорция). В тексте обсуждается идея перспективы, а также использование математики архитектурой. Также обсуждается то, что древние греки считали пятью совершенными телами. Монах был другом многих художников того времени. Одним из них был Леонардо да Винчи. Получив образование художника, да Винчи работал с Пачоли над иллюстрацией книги.Леонардо да Винчи предоставил для книги около шестидесяти рисунков. Некоторые из них включали геометрические фигуры для иллюстрации математических концепций.

Обучаясь у Пачоли, да Винчи использовал идею золотого сечения в некоторых своих картинах и рисунках. Его использование появляется в таких произведениях, как Тайная вечеря и Мона Лиза.

Перспектива

Когда дело доходит до математики и искусства, да Винчи использовал в своих работах математические принципы линейной перспективы.Три элемента, необходимые для линейной перспективы, — это параллельные линии, линия горизонта и точка схода. Он мог создать впечатление, будто объекты находятся дальше от зрителя. Да Винчи умел создавать иллюзию глубины на плоской поверхности, такой как картина или рисунок.

Изучив принципы линейной перспективы, да Винчи нашел хорошее применение в некоторых из своих ранних работ. В своей картине «Благовещение» он использует перспективу, чтобы выделить различные элементы, улучшающие произведения.Используя линейную перспективу, он включает такие элементы, как угол здания, огороженный сад и дорожку. В совокупности такие черты контрастируют замкнутостью и открытостью.

Из других его работ незаконченная «Поклонение волхвов» должна была показать степень познания Да Винчи в рисовании фигур и перспективе. В своей работе над картиной он произвел ряд этюдов. Это включало в себя глубокое изучение перспективы.Один из них фигурировал в левой части картины, где он планировал проиллюстрировать ее сложным фоном разрушенных классических зданий. Для этого он тщательно изучил перспективу.

Леонардо да Винчи в использовании перспективы признан первым, кто применил анаморфоз. Это метод, при котором изображение можно увидеть только с помощью изогнутого зеркала или из определенного положения.

Математика и работы да Винчи

Две из самых известных работ Леонардо да Винчи, в которых используется математика, — это Тайная вечеря и Мона Лиза.Каждый применяет математические принципы перспективы, золотого сечения и пропорций в своей композиции. В своей картине «Тайная вечеря» он использует золотое сечение, чтобы расположить различные элементы картины. Он использует соотношение для размещения людей в столе с пропорциями стен и окон на заднем плане. Используя математические принципы, да Винчи помогает объединить различные элементы картины.

Картина Да Винчи «Мона Лиза» использует в своей структуре золотое сечение.Некоторые видят красоту изображения в использовании золотого сечения. Центральные элементы композиции используют золотой прямоугольник по всей картине. Золотой прямоугольник — это прямоугольник, но разница заключается в размерах фигур. Размеры отражают золотое сечение. Золотое сечение видно на лице Моны Лизы. Если прямоугольник ограничивает лицо, и этот прямоугольник разделен линией, проходящей через ее глаза, образуется еще один золотой прямоугольник. В результате отношение длины головы Моны Лизы к ее глазам также соответствует золотому сечению.На остальной части тела можно нарисовать другие золотые прямоугольники.

Идеальные пропорции человека

Было поверье, что человек был совершенным творением, которое может описать математический закон. Было твердое убеждение, что математические принципы лежат в основе всех форм и подчиняются божественной пропорции. Многие считали человека самым совершенным творением Бога.Многие считали, что использование пропорций формирует человеческий облик.

Леонардо да Винчи использовал свои математические знания для создания ряда рисунков, показывающих то, что считалось идеальными человеческими пропорциями. Одной из самых известных его работ о человеческих пропорциях был «Витрувианский человек». Это визуальное изображение совершенной человеческой формы, созданное с помощью математики. Для таких людей, как да Винчи, математика была универсальной константой, позволяющей видеть пропорции повсюду.

«Витрувианский человек» да Винчи — это рисунок пером и тушью на бумаге, на котором изображен человек с вытянутыми руками и ногами. Мужчина появляется в наложенных друг на друга позициях, вписывающихся в круг и квадрат. Да Винчи использует картинку, чтобы показать нам значение различных пропорций человеческого тела. Поступая таким образом, он использует математику, чтобы описать идеальные физические характеристики человека. Для иллюстрации идеальных пропорций человеческого тела текст, который появляется вокруг рисунка, не менее важен.В тексте подробно описаны различные пропорции человеческого тела, описанные римлянином, известным как Витрувий, на которых да Винчи основывает свой рисунок.

Помимо Витрувианского человека, Леонардо да Винчи также создал ряд рисунков, на которых показаны пропорции головы человека. Стремясь продвигать свое искусство и улучшать свои знания, да Винчи создал ряд иллюстраций людей и их пропорций.

Геометрические фигуры

Именно благодаря сотрудничеству с Лукой Пачоли над его рукописью «De divina пропорционально» он заинтересовался геометрией.Он видел, что он уделял этой теме много времени. Интерес да Винчи к геометрическим фигурам, таким как многогранники, виден во многих набросках, разбросанных по его рисункам.

Для книги «De divina пропорционально» да Винчи создал шестьдесят иллюстраций геометрических форм на основе произведений и моделей Пачоли. Некоторые из иллюстраций были первыми многогранниками, на которых были видны твердые ребра. Рисуя формы таким образом, можно было видеть эти края спереди от тех, которые были сзади.Это устранило любую очевидную путаницу, которая могла возникнуть при простом рисовании линий. Наличие полых граней на форме означало, что можно было видеть сквозь структуру спереди и сзади. Геометрическая иллюстрация предоставила много полезной геометрической информации. Помимо многогранников, да Винчи создавал аналогичные рисунки для других геометрических фигур. Иллюстрации в основном создавались парами. Один показал модель с твердыми гранями, а другой использовал свою технику твердой кромки.

человеческих черепов по золотому сечению да Винчи

Золотое сечение, описанное Леонардо да Винчи и Лукой Пачоли как Божественная пропорция, представляет собой бесконечное число, которое часто встречается в природе, искусстве и математике. Это узор в сосновых шишках, ракушках, галактиках и ураганах.

В новом исследовании выясняется, соответствует ли форма черепа золотому сечению (1.618…), исследователи Джона Хопкинса сравнили 100 человеческих черепов с 70 черепами шести других животных и обнаружили, что размеры человеческого черепа соответствуют золотому сечению. Однако черепа менее родственных видов, таких как собаки, два вида обезьян, кролики, львы и тигры, расходились с этим соотношением.

«У других исследованных нами млекопитающих действительно уникальные соотношения, приближающиеся к золотому сечению с увеличением видовой сложности», — говорит Рафаэль Тамарго, доктор медицины, профессор нейрохирургии Медицинской школы Университета Джонса Хопкинса.«Мы считаем, что это открытие может иметь важные антропологические и эволюционные последствия».

Исследователи опубликовали свои выводы в сентябрьском номере журнала Craniofacial Surgery.

Золотое сечение можно рассчитать, разделив линию на две неравные части, причем длина более длинной части, разделенная на более короткую, будет равна всей длине, разделенной на более длинную часть. Интерес Тамарго к истории и анатомии побудил его в 2010 году опубликовать статью об обнаружении человеческого мозга и спинного мозга в изображении Бога на картине Микеланджело Сикстинской капеллы.

Джонатан Пиндрик, ныне детский нейрохирург в Национальной детской больнице в Огайо, также внес свой вклад в исследование.

Ссылка : Тамарго, Р. Дж., И Пиндрик, Дж. А. (2019). Размеры черепа млекопитающих и золотое сечение (Φ). Journal of Craniofacial Surgery, 30 (6), 1750. https://doi.org/10.1097/SCS.0000000000005610

Эта статья была переиздана на основании следующих материалов. Примечание: материал мог быть отредактирован по объему и содержанию. Для получения дополнительной информации, пожалуйста, свяжитесь с цитируемым источником.

Что такое золотое сечение и как его использовать в дизайне

Визуальный баланс и последовательность — ключ к хорошему дизайну. Если вы не дизайнер, то поначалу это может быть сложно. Но именно поэтому у дизайнеров есть визуальные инструменты для тренировки глаз и способностей. Золотое сечение — один из таких инструментов. Но что такое , золотое сечение ?

В этой статье мы поговорим о золотом сечении и о том, как использовать его в дизайне. Мы немного углубимся в математику, историю и немножко разоблачим мифы.Вы закончите этот пост, зная, почему так важно золотое сечение и как оно может помочь вам создавать визуально приятные визуальные эффекты с помощью Visme.

Все дело в восприятии. А теперь приступим!

Что такое золотое сечение?

Золотое сечение, также называемое золотым сечением или божественной пропорцией, — это термин, который часто упоминается в блогах о дизайне, книгах по искусству, исторических журналах, шоу о загадках вселенной и видеороликах о магии математики в природе.

Со временем золотое сечение приобрело своего рода известность и известность, которая одновременно вдохновляет и сбивает с толку людей. Золотое сечение — это математическое чудо и спорный миф о дизайне, объединенные в одну иррациональную концепцию.

Прежде чем пристрелить меня, позвольте мне объяснить. Золотое сечение — определенно вещь. Красиво несовершенная математическая вещь, которая может помочь дизайнерам создавать визуально сбалансированные проекты. Но это не надежное решение для создания красивых, идеально эстетичных дизайнов.

Золотое сечение и его геометрическая магия — это инструмент, как и любой другой, который может помочь дизайнерам улучшить свое визуальное сообщение. То же самое относится к использованию сеток документа, правила третей и сетки из 8 пунктов.

Вы здесь, потому что любите формы и геометрию? Тогда вам понравится это видео Visme об использовании фигур в дизайне!

Загадка золотого сечения

Если вы поищете в Интернете золотое сечение, вы увидите изображения Парфенона и Моны Лизы с золотой спиралью или золотым прямоугольником наверху.

Вы увидите фотографии ракушек, штормов и семян подсолнечника. И наряду с ними вы увидите Ветрувианского человека Леонардо да Винчи, Тайную вечерю Сальвадора Дали и, возможно, просто чертежи зданий Ле Корбюзье.

Как не дизайнер, и даже как дизайнер, в ваших интересах относиться ко всему, что, по вашему мнению, вы знаете о золотом соотношении, с недоверием.

Например, мы знаем, что значение золотого сечения обозначается греческой буквой фи.Но это не означает, что греки сделали это различие. Фактически только в 1900-х годах буква Фи была удостоена должности хранителя золотого сечения.

Термин «золотое сечение» был введен математиком Мартином Омом в 1800-х годах, а до этого его называли «Божественная пропорция» Лука Пачоли и Леонардо да Винчи.

Первое упоминание об этом числе в истории Греции находится в книге Евклида Александрийского, где он упомянул «крайнее и среднее соотношение.”

Это правда, что греки очень интересовались математикой и геометрией и использовали математические вычисления в своем искусстве и архитектуре. Но идея о том, что они построили все по золотому сечению, особенно Парфенон, весьма вероятно, всего лишь миф.

Все дело в восприятии красоты

Важность золотого сечения и его актуальность в искусстве, архитектуре и дизайне связана с восприятием красоты и эстетики.

Психологически человеческий мозг воспринимает изображения с золотыми пропорциями как более приятные визуально, чем изображения без них.

Это теория, которую нельзя полностью доказать, но она много изучалась, чтобы выяснить, почему наш мозг сообщает нам, что одни вещи приятны, а другие — нет.

Считается, что золотое сечение обладает магической способностью придавать вещам присущую им красоту, так что наш мозг воспринимает их как прекрасные. Что не доказано, так это то, что мы научились думать так или это научно верно.

Тем не менее, золотое сечение стало таким же известным, как и стоящие за ним противоречивые убеждения.

Основная популярность золотого сечения началась в эпоху Возрождения, когда Лука Пачоли написал свою книгу De Divina Proportione . В этой книге он объяснил «божественную пропорцию» и то, как она была высшим выражением красоты в природе и человеческой форме.

Леонардо да Винчи проиллюстрировал концепцию Витрувианского человека.

Источник изображения

Давайте на минутку распакуем.Термин «божественное» — это слово для чего-то святого, происходящего с небес. Это прилагательное с благочестивой природой. Божественная пропорция — это мера, цель которой объяснить «совершенство».

Идеальные тела, идеальные лица, идеальные здания, идеальные растения. Если логично следовать этому ходу мыслей, тогда идеально = красиво.

Обладая повышенным магическим качеством, присваиваемым золотому сечению со временем, он стал без вопросов символом красоты и эстетики.

Но спросите себя: как можно использовать геометрический инструмент, который якобы объясняет идеальные пропорции формы, объекта или дизайна, чтобы превратить что-либо в красивую вещь?

Как создатели контента и люди, важно помнить, что красота относительна. Идеальное не значит красивое, как бы общество ни пыталось его проглотить.

Да, в вещах есть определенное качество, благодаря которому дизайн выглядит эстетично и приятно для глаз.Это называется балансом. А баланс довольно часто бывает «несовершенным».

Золотое сечение — выдающийся пример магии математики. Вот почему это важно. Не для того, чтобы делать вещи красивыми, а для того, чтобы помочь найти баланс в повседневных вещах.

Пока вы используете золотое сечение и его геометрические инструменты в этом отношении, ваши рисунки будут более эстетичными, приятными для глаз, хорошо сбалансированными и, следовательно, лучше воспринятыми вашими зрителями.

Но, пожалуйста, не поддавайтесь заблуждению, что наложение золотой спирали на любую композицию и корректировка ее по размеру сразу же сделает ее красивой.

Магическая математика

Математически золотое сечение — это иррациональное число, полученное в результате вычислений для описания хорошо сбалансированной пропорции.

Числовое значение золотого сечения «Фи» широко известно как 1,618 …

Вы можете увидеть математическую формулу ниже вместе с полезной визуализацией.

Самый длинный раздел, разделенный на самый короткий, равен сумме обоих, разделенных на самый длинный. Они, в свою очередь, равны 1.618 …

Самый простой способ визуализировать, как работает соотношение, — это золотой прямоугольник и золотая спираль внутри него. Золотой прямоугольник разделен на две части в соответствии с золотым сечением.

Спираль создается, поскольку прямоугольник непрерывно разделяется на более мелкие части с использованием того же соотношения.

Последовательность Фибоначчи и ее связь с золотым сечением

В 1200 году нашей эры математик Леонардо Ди Пиза расшифровал соотношение наоборот.Из своих вычислений он получил строку чисел, которая теперь называется последовательностью Фибоначчи.

Последовательность выглядит так:

1,1,2,3,5,8,13,21…

Чтобы вычислить следующее число, вы должны сложить два последних числа и затем повторить то же уравнение. Это может продолжаться вечно.

Числа в последовательности Фибоначчи не соответствуют золотому сечению, но очень близки. На самом деле настолько близки, что их часто связывают вместе.

Золотое сечение использует разделение для визуализации своей цели, в то время как последовательность Фибоначчи начинается с малого и растет оттуда.Кроме того, поскольку золотое сечение иррационально, невозможно определить его точное число.

Вот почему эта визуализация золотого прямоугольника, разделенного на квадраты, содержит числа Фибоначчи внутри каждого квадрата.

В выступлении на TED ниже Артур Бенджамин объясняет, как работают числа Фибоначчи и как они связаны с золотым сечением. Это всего лишь краткий обзор того, как работает эта последовательность, но отличное место для начала.

Это поможет вам понять, почему последовательность Фибоначчи и золотое сечение так часто связаны вместе.

Совершенная иррациональность золотого сечения

Математически золотое сечение — иррациональное десятичное число. Интересно то, что когда он раздроблен внутри себя, он на самом деле довольно совершенен.

Этот секрет золотого сечения — это то, что предлагает беспрецедентную художественную лицензию при его использовании в визуальных проектах. Мы объясним, как это происходит, в разделе о том, как золотое сечение присутствует в природе.

Если вы хотите узнать больше о том, почему золотое сечение является совершенно иррациональным числом и почему это важно, посмотрите это видео.

Ведущий использует семена подсолнечника, чтобы визуализировать, как природа использует золотое сечение и последовательность Фибоначчи как совершенно иррациональный способ быть практичным при выращивании семян.

Как золотое сечение присутствует в природе? Разрушение мифов о золотой спирали

Золотое сечение или божественная пропорция, по-видимому, присутствует в природе разными способами.От того, как лист папоротника раскрывается по спирали, до формы урагана, видимого со спутника.

Самая распространенная естественная визуализация, которую вы увидите в сотнях опубликованных статей о золотом сечении в природе, — это спираль. Обычно это ракушки наутилуса, ураганы и папоротники.

Когда вы видите в природе что-то похожее на золотую спираль, чаще всего это не так в математическом смысле.

Большинство спиралей, используемых в природе в качестве примеров золотой спирали, являются логарифмическими спиралями.Их коэффициент вращения составляет от 1 до 2, но не совсем 1,618…

.

Эти логарифмические спирали очень напоминают золотую спираль в той точке, где ваш глаз воспринимает их как таковые. Вот почему они используются в качестве примеров в бесчисленных опубликованных статьях о золотом сечении.

Это возвращает нас к тому, насколько влияние золотого сечения считается математиками мифом.

Когда дело доходит до того, как использовать золотое сечение в дизайне, этот миф на самом деле полезен.Почему? Потому что это означает, что вам не нужно точно соблюдать пропорции, чтобы ваш дизайн был визуально приятным. Просто нужно быть предельно близко к этому!

Ниже вы увидите изображения элементов в природе и космосе, которые, казалось бы, настолько точно следуют золотому сечению, что естественным образом создают визуально сбалансированную и привлекательную спираль.

Как последовательность Фибоначчи присутствует в природе?

Теперь, когда мы взглянули на то, как золотая спираль присутствует в природе, давайте посмотрим, как последовательность Фибоначчи применима к загадке.Как мы уже говорили выше, эта последовательность чисел очень напоминает золотое сечение.

Последовательность Фибоначчи очень часто присутствует в том, как семена подсолнечника выходят из центра цветка по спирали. Но не только это. Последовательность может предсказывать такие природные явления, как размножение кроликов, ветвление дерева и количество лепестков на цветке.

Все естественные спирали, указанные выше, можно измерить с помощью последовательности Фибоначчи в логарифмической спирали, но в приведенных ниже примерах последовательность присутствует больше.

Как использовать золотое сечение в дизайне

Наконец-то мы подошли к лучшему!

Давайте посмотрим, как использовать золотое сечение в дизайне.

Для не дизайнера понять, когда слайды презентации, инфографика или графика в социальных сетях визуально сбалансированы, непросто. К счастью, есть инструменты, которые упростят вам задачу. Золотое сечение — одно из них.

Если вы читали разделы выше о головоломках золотого сечения и восприятии красоты, вы уже знаете, что использование золотого сечения не означает, что ваш дизайн автоматически будет красивым по своей сути.

Уловка использования золотого сечения состоит в том, чтобы найти баланс. Всегда дело в балансе.

Несмотря на то, что многое из того, что считается золотым сечением, не обязательно может быть правдой, это не значит, что вы не можете проектировать с его помощью!

Давайте рассмотрим, как можно использовать золотое сечение в своих проектах.

Визуальная геометрия золотого сечения

Золотое сечение имеет несколько различных форм, чтобы помочь вам достичь баланса в ваших проектах Visme.

Это:

• золотой прямоугольник
• золотая спираль
• золотой треугольник
• сетка фи

Кроме того, вы также можете иметь составные круги, спирали и треугольники, которые образованы комбинацией любого из вышеперечисленных.

Существует большое пересечение между искусством и геометрией, называемое «сакральной геометрией», которая использует принципы золотого сечения и последовательности Фибоначчи в качестве основы форм. Это может не помочь в дизайне, но определенно вдохновит на творчество!

Золотой прямоугольник

Первая и самая простая из золотых геометрических фигур — золотой прямоугольник.На рисунке ниже изображен идеальный золотой прямоугольник, который вы можете использовать для наложения на свой дизайн и соответствующей настройки элементов.

Используйте некоторые области, чтобы создать белое пространство. Затем используйте линии и пересечения для создания точек фокусировки.

Скачать здесь

Золотая спираль

Золотая спираль и золотой прямоугольник похожи в том, как вы можете использовать их в своих проектах. Спираль добавляет новый набор пересекающихся изогнутых линий, которые могут помочь создать новые области фокусировки и интересные формы и цвета.

Золотые треугольники

Пропорция золотых треугольников немного сложнее. Но он определенно может помочь с дизайнами, в которых используются диагональные формы и визуальные пространства.

Фи Сетка

Еще один инструмент золотого сечения, который поможет вам создавать дизайнерские композиции, — это сетка Фи. Это очень похоже на правило третей, поэтому, если вы уже использовали эту сетку, освоить ее будет несложно.

Составные геометрические композиции

Наконец, это геометрические композиции с использованием золотого сечения.Это могут быть как две золотые спирали вместе, так и сочетание форм в золотых пропорциях. Например, если вы поместите две золотые спирали лицом друг к другу, из них получится сердце.

Золотые пропорции без золотых фигур

Есть еще один способ включить золотое сечение в свои проекты, не прибегая к золотым формам. Вам просто нужно использовать золотую пропорцию 1,618.

Например, это набор квадратов с двумя секциями в золотых пропорциях.Длина одной из сторон делится на 1,68, и меньшая часть имеет решение в виде высоты. 1000 / 1,618 = 618.

Ниже представлена ​​та же система, примененная к графическому изображению в размере обложки Facebook.

А вот и он в стандартном размере слайда презентации.

Золотое сечение в искусстве и архитектуре

Леонардо да Винчи был первым проверенным художником, который использовал золотое сечение в своем изображении ветрувианского человека. Если он действительно использовал это соотношение для Моны Лизы, вероятно, это останется загадкой на все остальное время.

Нам даже не поехать на Парфенон в Афинах, Греция. Интернет скажет вам, что он был создан с использованием золотого сечения, но математика скажет вам обратное.

Чтобы понять, как на самом деле используется золотое сечение в дизайне, мы должны взглянуть на работы Сальвадора Дали и Ле Корбюзье. Это два творца, которые сознательно и систематически использовали золотое сечение для создания своего искусства.

Самым известным изображением золотого сечения Сальвадора Дали является его картина 1950-х годов под названием Таинство Тайной вечери .

Он использовал сетку phi для установки элементов на холсте. Дали также включил додекаэдр над таблицей. В форме додекаэдра геометрически укоренилось золотое сечение.

Источник изображения

Ле Корбюзье — швейцарский французский архитектор, который использовал золотое сечение для создания системы дизайна под названием Modulor , основанной на вымышленном человеческом теле, разделенном на божественные пропорции.

Его идея Modulor заключалась в создании системы, позволяющей дизайнерам и архитекторам проектировать функциональные жилые помещения в гармоничных пропорциях.

Источник изображения

Золотое сечение в фотографии

Использование золотого сечения в качестве инструмента композиции довольно распространено в фотографии. Фотографы используют правило третей, а другие используют золотое сечение либо в прямоугольнике, либо в спирали, либо в сетке фи.

Настройка композиции фотографии для соответствия золотому сечению выполняется частично во время съемки фотографии и до некоторого уровня на этапе редактирования. Наложив на фотографию золотой прямоугольник, спираль или сетку, фотограф может увеличить кадрирование или настроить фотографию в соответствии с ней.

Вот несколько примеров того, как золотое сечение используется в фотографии для создания композиции.

Когда дело доходит до использования фотографии и золотой сетки в дизайне, вы можете использовать золотое сечение для соответствующей настройки фонового изображения, а затем содержимого наверху.

Золотое сечение в дизайне логотипов

Был ли Apple действительно разработан с использованием золотого сечения? Если вы выполните поиск в Google дизайна логотипа с золотым сечением, одним из первых результатов будет эта графика, утверждающая, что логотип Apple был разработан с использованием этого отношения.

Несмотря на то, что этот миф был развенчан, он все еще фигурирует во многих статьях о золотом сечении, используемом в дизайне.

В разоблачении автор объясняет, почему изгибы и формы логотипа яблока не точно соответствуют золотому сечению. Создателю рисунка ниже пришлось манипулировать кругами и самим логотипом, чтобы кривые точно соответствовали кривым круга.

Кроме того, круги вообще не соответствуют золотому сечению. Это только выглядит так, потому что им манипулировали.

Тот факт, что логотип Apple на самом деле не был разработан с использованием золотого сечения, но в любом случае выглядит хорошо, является доказательством того, что даже если ваш дизайн «близок» к золотому сечению, он все равно может выглядеть сбалансированным и визуально привлекательным.

Нет необходимости точно соблюдать золотое сечение. Помните, что десятичная цифра золотого сечения иррациональна и не имеет конца.

Источник изображения

Несмотря на то, что логотип Apple был разоблачен как разработанный с использованием золотого сечения, есть пара суперславных логотипов, которые действительно были такими.

Журнал National Geographic представляет собой буквально золотой прямоугольник, и Pepsi также включает золотое сечение в свой фирменный логотип.

Источник изображения

Ниже представлен логотип, созданный с использованием золотого сечения. Наш дизайнер использовал золотой прямоугольник, спираль и составные круги, чтобы выбрать формы в пропорциях золотого сечения. Затем она собрала их вместе, используя золотое сечение в качестве макета.

Вы можете создать логотип с помощью Visme, используя золотое сечение, так же, как это сделал этот дизайнер.Посетите создателя логотипов Visme, чтобы получить множество идей.

Золотое сечение в слайдах презентации

Можете ли вы использовать золотое сечение для создания слайдов презентации? Конечно, почему бы и нет! Вы можете наложить любую из геометрических фигур золотого сечения, чтобы разложить композицию слайдов.

Не используйте одно и то же решение стиля на каждом слайде, так как это может сделать его повторяющимся. Баланс также складывается из разнообразия.

Найдите идеальный шаблон для своей следующей презентации! Просмотрите сейчас

Золотое сечение — только одно в большом наборе инструментов дизайна

На этом сегодня все, что касается золотого сечения и того, как его использовать в дизайне.Давайте посмотрим, что мы узнали:

• Золотое сечение — это математическое уравнение, которое визуализирует пропорцию между двумя частями золотой формы.
• Последовательность Фибоначчи тесно связана с золотым сечением и присутствует в натуральных логарифмических спиралях.
• Многое из того, что Интернет говорит о золотом сечении в древнем искусстве и архитектуре, вероятно, является мифом.
• Золотое сечение — это физическое приближение к пропорциям, которые наш мозг воспринимает как прекрасное.
• Вы можете использовать золотое сечение для создания хорошо сбалансированных дизайнов на Visme с помощью ряда техник.

Самое важное, что нужно помнить о золотом сечении, — это то, что это лишь один из многих инструментов, имеющихся в вашем распоряжении при создании визуальных ресурсов для вашего бизнеса.

Не полагайтесь исключительно на золотое сечение и даже не используйте его, если не хотите! Думайте об этом как о свободной визуальной сетке, которая поможет вам создавать сбалансированные композиции.

Каково же тогда золотое соотношение? Это лишь один из обширного набора инструментов дизайна, который поможет вам создать визуально привлекательную графику для вашего блога, бизнеса или профилей в социальных сетях.Зарегистрируйте учетную запись Visme и начните создавать все эти активы уже сегодня!

Золотое сечение несколько запятнано

Авторы: Буркард Польстер и Марти Росс

The Age, 18 мая 2009 г.

Мы только что написали о прекрасных узорах в «Ангелах и демонах», поэтому сейчас самое время обсудить гораздо менее впечатляющую математику в более известном романе Дэна Брауна «Код да Винчи». Хотя, честно говоря, не во всем виноват Дэн.

Золотое сечение, Золотое сечение, Божественная пропорция … Такие великие титулы должны указывать на поистине чудесную концепцию, да? Ну и да, и нет.

Золотое сечение — это, пожалуй, величайшая математическая причуда всех времен. В «Коде да Винчи» искусствовед, герой Роберт Лэнгдон, читает расширенную лекцию о числе 1.618, которое он представляет как φ, греческую букву «фи». Это число предположительно является золотым сечением.

Лэнгдон приводит впечатляющий список случаев появления φ в искусстве и природе, включая греческий Парфенон и Витрувианский человек да Винчи: оба они очень хорошо знакомы φ-фаддистам.Но, за немногими исключениями, эти предполагаемые случаи в лучшем случае сомнительны, а в худшем — просто глупы. Мы не можем здесь описать всю эту глупость (спросите нас как-нибудь о раковинах наутилуса), но мы приступим.

Идея золотого сечения восходит к Евклиду более 2000 лет назад. Однако грандиозные имена и причуда начались в 1500-х годах с итальянца Луки Пачоли.

Излишне говорить, что Евклид и Пачоли не просто решили, что 1,618 — отличная идея для ряда.Фактически, φ = 1,618… (точки важны, потому что они показывают, что φ — иррациональное число) естественно возникает как решение геометрических задач.

Проще говоря, мы можем рассмотреть идею золотого прямоугольника. Это прямоугольник с правильными пропорциями, так что если мы удалим квадрат, то останется повернутый прямоугольник с такими же пропорциями. Записывая L и W для длины и ширины прямоугольника, мы устанавливаем φ = L / W как отношение этих сторон. Приложив немного усилий, мы можем получить уравнение для φ, и положительное решение этого уравнения равно 1.618…

Математика φ поистине прекрасна. Например, мы можем продолжать удалять квадраты, создавая нисходящее гнездо квадратов и золотых прямоугольников; это бесконечное гнездо имеет алгебраический аналог — красивую цепную дробь

Золотое сечение также тесно связано со знаменитыми числами Фибоначчи — история для другого дня.

Но что эта математическая красота означает для появления φ в искусстве? Очень мало. Изображения золотых прямоугольников, вписывающихся в Парфенон, явно надуманы.И нет никаких свидетельств того, что Фидий, архитектор Парфенона, знал о концепции золотого прямоугольника.

Предполагаемое появление φ у Витрувианского человека вдвойне неверно. Предполагается, что для человека с хорошими пропорциями общий рост, деленный на рост до пупка, должен равняться φ. Просто нет свидетельств того, что человеческое тело каким-либо образом содержит φ. И исторически Витрувианский Человек даже не смоделирован на основе какой-либо теории, включающей ф.

И так продолжается и продолжается. Стремление одобрить искусство и художников золотым сечением привело к необычным возням с числами и историей. Роза под любым другим названием может быть столь же сладкой, но мы задаемся вопросом, насколько популярным был бы φ, если бы он был просто известен как «фракция Евклида».

Copyright 2004-∞ Все права защищены.

Как мы раскрыли тайну кода Да Винчи о происхождении жизни | Дэвид Самптер

Книга Дэна Брауна «Код да Винчи» захватила мое воображение с первой страницы.Обстановка в мире искусства и на академических факультетах, расследование убийства и теория заговора — вот все, чем не является моя университетская жизнь, но могло бы быть, если бы я закрыл глаза и немного пофантазировал. Он показал, как мы, академики, видим себя в поисках истины в последней инстанции. И, что действительно меня поразило, это его объединяющая тема золотого сечения, фи = 1,618…, божественная пропорция, которая, по словам героя книги профессора Лэнгдона, лежит в основе всего, от искусства до биологии и религии.

«Никто лучше Да Винчи не понимал божественную структуру человеческого тела». — утверждает профессор Лэнгдон. Эти типы наложений золотого прямоугольника, у которых длина сторон имеет отношение phi = 1,618…, предназначены для того, чтобы показать, что рисунок Виртрувианского человека, сделанный Да Винчи, следует божественной пропорции.

Хотя я был вдохновлен, я никогда не был полностью убежден вымышленным описанием Фи Брауном. Математика, которую я использую профессионально, очень отличается от богоподобной симметрии, описываемой как Код.Конечно, в математике есть несколько замечательно полезных универсальных констант, включая фи, пи (3,14…), константу Эйлера (0,577…), натуральное число e (2,71…) и многие другие. Но у каждого из них есть свои ограничения и они возникают из вполне конкретных областей математического исследования (фи из решения последовательности Фибоначчи, пи из кругов, константа Эйлера из логарифмического роста, e из экспоненциального роста и т. Д.).

После публикации книги Брауна математики отметили, что многие утверждения профессора Лэнгдона о фи не выдерживают научной проверки.Рисунок выше, на котором золотые прямоугольники наложены на рисунок да Винчи, произвольный, как и те, которые часто изображают Парфенон в Греции. Есть много разных точек и линий на человеке или здании, которые мы можем измерить, и некоторые из них по совпадению будут близки к фи. За исключением случаев появления чисел Фибоначчи в подсолнухах, никакой конкретной роли фи в природе не установлено.

Интернет, конечно же, продолжает зацикливаться на цифрах. Они верят, как драматично провозгласил в своей книге профессор Лэнгдон, что « древние считали, что число PHI, должно быть, было предопределено Создателем вселенной…»

Делали ли греки и люди, жившие в эпоху Возрождения, такое предположение? спорно, но сегодня легко найти блоги и веб-страницы, делающие подобные заявления.На протяжении всей истории некоторые из нас пытались найти предопределенный порядок в числах. Исследования показывают, что обычно мы ошибаемся.

Но могли ли современные математики недооценить силу фи?

Я не особо задумывался о коде да Винчи до тех пор, пока в прошлом году мой аспирант Юй Эрнест Лю зашел в мой офис, чтобы обсудить результаты своего последнего компьютерного моделирования. Эрнест показал мне распечатки графиков результатов своего моделирования, на которых он нацарапал десятичные дроби 1.618 ручкой поверх некоторых графиков.

«Это число продолжает расти, — сказал мне Эрнест, — как соотношение между темпами роста химических веществ. Я посмотрел на него, и это называется Золотое сечение. Я не уверен, почему он находится здесь… »

Эрнест уже осознал возможное значение этого открытия. Его докторский проект немного отличался от большинства других: он использует математику для исследования происхождения жизни. Последние три года он работал над созданием химической модели, объясняющей, как возникает самовоспроизведение.Его вопрос заключается в том, как Вселенная превратилась из супа химических реакций, чтобы включить богатое разнообразие биологического воспроизводства, которое мы называем жизнью. Было интересно найти фи в контексте этого вопроса.

Может быть, скептики ошибались и фи могла быть предопределенным результатом моделирования воспроизводства? Может ли золотое сечение дать код Да Винчи самой жизни?

Эрнест и я начали с чтения научной литературы, и оказалось, что некоторые биологи-математики уже увидели потенциальную роль фи в самовоспроизводстве.Исследователи из Бразилии показали, что частоты человеческих нуклеотидов аденина и цитозина соответствуют золотому сечению, а один независимый исследователь из Франции заявил, что геном человека «точно настроен» на фи. Ученые все еще верили в то, что фи является универсальным свойством биологии.

Тон этих статей был интригующим. Нам нужно было точно исследовать, как наши новые результаты вписываются в эту работу.

Эрнест обнаружил, что самовоспроизведение было общим свойством многих химических вселенных, которые он моделировал, и именно в рамках некоторых из этих моделей могло появиться соотношение фи.Но были и другие модели, дающие другие соотношения. Иногда он обнаруживал, что важным соотношением было 1,324… (число, известное как пластическое число), в других случаях оно составляло 1,220… (третье нижнее золотое сечение) или 1,259… (третий корень из 2), а в некоторых симуляторах он вообще не мог найти никакого соотношения. Важно отметить, что фи больше не было самым распространенным соотношением, это было одним из многих интересных чисел, которые появлялись повсюду.

Коэффициенты, использованные при моделировании Эрнеста. Фи (1.618 ..) не было получено даже самого общего соотношения.

Чтобы разгадать эту загадку, Эрнест начал записывать уравнения, описывающие каждое из различных самовоспроизводящихся имитаций, которые он запускал. Затем, решая их по мере того, как время стремится к бесконечности, Эрнест обнаружил, так называемое, характеристическое полиномиальное уравнение для каждого случая. Один из примеров этого уравнения показан ниже

, и решением этого уравнения является не что иное, как лямбда = (1 + sqrt (5)) / 2 = phi.

Теперь мы увидели, что в фи нет ничего особенного.Каждый характеристический многочлен имеет свое собственное решение, и теперь Эрнест мог определить, почему каждое из чисел лежит в основе каждого из его симуляций химической жизни.

И их не было ни одного, ни даже двух. На самом деле их было много, бесконечно много. Фи и все другие числа, найденные Эрнестом, были алгебраическими числами, которые показаны на графике ниже.

Алгебраические числа на комплексной плоскости. Создано Дэвидом Муром. Подробнее об этом читайте здесь.

Это изображение, возможно, даже более потрясающее, чем наложение золотых прямоугольников друг на друга на рисунке Да Винчи.И было бы заманчиво, демонстрируя эту картину, вернуться к образным философским размышлениям вымышленного профессора Лэнгдона. Может быть, такая фигура хранит секреты жизни? Каждое решение для самовоспроизведения запечатлено в ярком и бесконечном сиянии?

Это просто не так. Настоящая наука и математика так не работают, даже если нам иногда это нравится. Математика излучает много красоты, но эта красота — лишь малая часть истины. Мы с Эрнестом обнаружили и опубликовали в нашей научной статье, что алгебраические числа не являются ключом к самовоспроизведению.В нашем исследовании важно показать, что множество различных химических вселенных могут производить самовоспроизведение и жизнь (я скоро напишу об этих открытиях!).

Когда я был моложе, я мечтал о чем-то вроде кода да Винчи, объединяющем уравнении жизни. Вот почему книга захватила мое воображение. Некоторые теоретики, Макс Тегнмарк и Стивен Вольфрам, являющиеся двумя наиболее яркими примерами, по-прежнему полагают, что во Вселенной может быть скрытый код. Я крайне сомневаюсь.Мы видим проблески симметричной красоты в математике. Но настоящая красота в том, что для реальности не существует единого числа или уравнения. Мир, в котором мы живем, сложен, красив, запутан и порой невозможно понять. Никогда не будет единого уравнения, объясняющего почему.

Новый код да Винчи? Божественная пропорция, найденная в человеческих черепах

Витрувианский человек Леонардо с золотыми пропорциями выделен.

Источник: Источник: Изменено Рафаэлем Тамарго

Более 500 лет назад Леонардо да Винчи создал иллюстрации к книге О божественной пропорции (De Divina Proportione), , которая была написана в 1498 году и впервые опубликована в 1509 году.В этой оригинальной рукописи исследуются, казалось бы, «мистические» математические пропорции, которые в наше время обычно называют «золотым сечением».

Золотое сечение (Phi, или Φ ≈ 1,618) повсеместно присутствует в природе и часто применяется в изобразительном искусстве и скульптуре, а также в архитектуре; Золотое сечение создает структурно надежные и эстетически привлекательные здания.

Ранее на этой неделе два нейрохирурга из Медицинской школы Университета Джона Хопкинса сообщили (Tamargo & Pindrik, 2019), что золотое сечение (Φ) наблюдается в архитектуре человеческих черепов, но (что удивительно) не присутствует в пропорциях черепа. другие млекопитающие.Эти данные были опубликованы в сентябрьском выпуске журнала Journal of Craniofacial Surgery .

Золотое сечение характеризует уникальные отношения в изучении целых чисел, раздел математики, называемый теорией чисел. Численно Φ можно рассчитать как отношение в пределах ряда Фибоначчи, когда ряд приближается к бесконечности.

Источник: Рафаэль Тамарго и Джонатан Пиндрик / Журнал черепно-лицевой хирургии. (Открытый доступ)

Для этого исследования Рафаэль Тамарго и Джонатан Пиндрик тщательно измерили пропорции 100 человеческих черепов и 70 черепов шести других видов млекопитающих.Затем они вычислили пропорцию и соотношение между отдельными регионами.

Примечательно, что авторы обнаружили, что у людей два важных отношения приблизительно соответствуют золотому сечению. Однако у шести других видов млекопитающих оба этих соотношения не отражают так называемые «божественные пропорции» или Φ.

Источник: Pixabay

Согласно Тамарго и Пиндрику, «разница между соотношениями показала тенденцию к конвергенции по Ф, коррелирующей со сложностью видов». Черепа таких видов, как собаки, два вида обезьян, кролики, а также львы и тигры, расходились по золотому сечению.

«У других исследованных нами млекопитающих действительно уникальные соотношения, приближающиеся к золотому сечению с увеличением видовой сложности», — сказал Рафаэль Тамарго, профессор нейрохирургии в JHUSM, в пресс-релизе Johns Hopkins. «Мы считаем, что это открытие может иметь важные антропологические и эволюционные последствия».

Как пишут Тамарго и Пиндрик в заключении статьи: «Мы предполагаем, что принцип золотого сечения, который был задокументирован в других биологических и природных системах, может также присутствовать в архитектуре и эволюции человеческого черепа.«

Рафаэль Тамарго всю жизнь страстно увлекался изучением пересечения искусства и нейроанатомии. В 2010 году он опубликовал статью «Скрытая нейроанатомия в книге Микеланджело « Отделение света от тьмы в Сикстинской капелле »» в журнале Neurosurgery .

Для этого исследования Тамарго и Ян Сук, медицинский иллюстратор, определили анатомически правильные изображения спинного мозга и ствола мозга человека на картине Сотворение Адама на центральной панели потолка Сикстинской капеллы. Scientific American опубликовал увлекательную статью (с большим количеством фотографий) Р. Дугласа Филдса об этом открытии.

Источник: Viking / Public Domain

Золотое сечение, божественные пропорции и ткань разума

Мой отец, Ричард Бергланд (1932–2007), был нейрохирургом конца 20 века, которого обучал Бронсон Рэй, протеже Харви Кушинга (1869–1939). Кушинг был одним из первых нейрохирургов начала 20-го века в больнице Джона Хопкинса, которого многие считают «отцом» современной нейрохирургии.

Как вы можете видеть на этом суперобложке, мой отец написал The Fabric of Mind . Мне нравится композиция на обложке этой книги. Тем не менее, еще в 1980-х годах ему пришлось изо всех сил убедить своего издателя поместить это графическое изображение мозга на обложку книги, предназначенную для широкого круга читателей.

Когда разрабатывался макет обложки папиной книги, люди из отдела маркетинга выразили обеспокоенность тем, что этот сагиттальный срез человеческого мозга был слишком «посмертным» и не понравится массовой аудитории.Может, они были правы; книга не была бестселлером. Тем не менее, мой отец считал, что это красивое изображение, точно отображающее изысканные пропорции и архитектуру мозга Homo sapiens .

Сегодня утром, читая длинное новое исследование Рафаэля Тамарго, я с ностальгией вспомнил подробные разговоры о неврологии, которые у меня с отцом были. Я бы хотел, чтобы папа был здесь, чтобы объяснить историческое значение этого недавнего открытия Φ за чашкой кофе, используя термины непрофессионала.

По совпадению, как и Рафаэль Тамарго, мой отец был очарован пересечением искусства и нейроанатомии. В качестве хобби папа делал скульптуры мозга из глины. Будучи скульптором-любителем и исследователем мозга, мой отец боготворил Микеланго и Леонардо да Винчи.

По причинам, которые я никогда полностью не понимал, мой отец был фанатично одержим набросками Леонардо из Divina Proportione . Степень его интриги с золотым сечением всегда казалась мне чем-то «незаметным».Папа зашел так далеко, что напечатал иллюстрации да Винчи божественной пропорции на огромных плакатах и ​​повесил их в своем офисе.

Когда мой отец хотел воплотить в жизнь нейробиологию или романтизировать историю науки о мозге, он рассказывал истории о том, как Леонардо да Винчи был пионером нейроанатомии эпохи Возрождения, опередившим свое время.

Как ни странно, папа говорил что-то вроде: «В 1504 году Леонардо да Винчи сделал восковую слепку человеческого мозга и ввел термин мозжечок (лат.« Маленький мозг ») после того, как заметил два маленьких полушария в форме кумквата, аккуратно спрятанных под ним. гораздо большие полушария головного мозга.«

К сожалению, мне очень мало удалось подтвердить анекдотические истории моего отца о Леонардо да Винчи с помощью Google Scholar, что разочаровывает. Поэтому с тех пор, как в 2007 году умер мой отец, я искал любую научную литературу по нейробиологии, в которой упоминается Леонардо да Винчи.

Вчера днем, когда мой телефон зазвонил с предупреждением Google об этом новом исследовании, я чуть не упал со стула.