Как найти центр в окружности – Как определить центр окружности 🚩 как найти центр круга 🚩 Математика

Как определить центр круглой детали. Как найти центр круга. Круг и окружность. Как найти центр

Нередко домашнему мастеру надо найти центр окружности или круглой детали. Я уже писал об одном из способов решения этой задачи в статье «как найти центр круга». Но у него есть один существенный недостаток — необходимо точно найти середину хорды и точно построить перпендикуляр из него.

К счастью, существует и другой метод точного нахождения центра круга не требующий никаких точных измерений. Он основан на том простом принципе, что если в окружность вписать прямоугольный треугольник, то его гипотенуза (самая длинная сторона) — будет диаметром этого круга или окружности.

Это подтверждается тем, что сумма углов треугольника равна 180 градусам. А весь круг — это 360 градусов. И любой прямоугольник, чья гипотенуза равна диаметру круга – будет прямоугольным. И наоборот — любой прямоугольный треугольник своей гипотенузой представляет диаметр круга.

А что нам даст центр круга точнее, как не пересечение двух диаметров круга?

В качестве «источника» прямого угла проще всего взять лист писчей бумаги. На комбинатах по производству бумаги их рубят с очень высокой точностью. Можно воспользоваться страницей какого либо журнала и т.п.

На круглую деталь накладываем лист бумаги так, что бы один его угол находился на окружности или крае круга. И отмечаем точки, где лист соприкасается другими краями с кругом. Отмечаем эти точки.

Проводим прямую линию между отмеченными точками. Расстояние между ними является диаметром этого круга. Обрезаем лишнюю бумагу и проводим на детали прямую линию — диаметр.

Достаточно переместить наш треугольник в другое положение и нарисовать еще один диаметр круга, как тут же в точке пересечения диаметров мы и получим искомый центр окружности…

Таким образом, не проводя абсолютно никаких измерений, мы можем найти центр любой окружности.

Константин Тимошенко (с) 01.04.2009

www.delaysam.ru

Как найти центр окружности : Ответ к задаче-головоломке |

 Ответ к задаче-головоломке №3: “Как найти центр окружности”

В статье “Задача-головоломка №3: “Как найти центр окружности”

было предложено найти центр окружности без использования специальных чертежных инструментов.

Сейчас можно ознакомиться с решением.

Шаг 1.  Возьмите картонный квадрат и положите кончик одного угла на любую точку окружности. Теперь в точках А и В, где стороны квадрата пересекают окружность, сделайте две отметки: (рис.1)

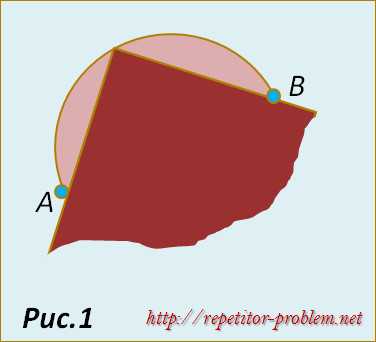
Шаг 2. Используя картонку как линейку, соедините прямой линией точки А и В. Теперь, поместив угол картона в   другой точке окружности, повторите действия первого этапа, отметив точки C  и D (Рис.2)

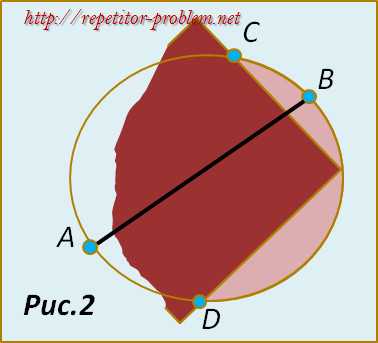
Шаг 3.  Проведите прямую линию из C и D.

Получили центр окружности . Он будет находится в точке пересечения линий АВ и CD (рис.3)

 

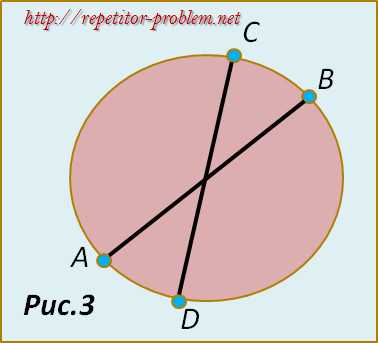
Обосновать это решение можно, опираясь на известный геометрический факт , который изучают в курсе геометрии 8 класса в теме “Вписанные углы”: 

 

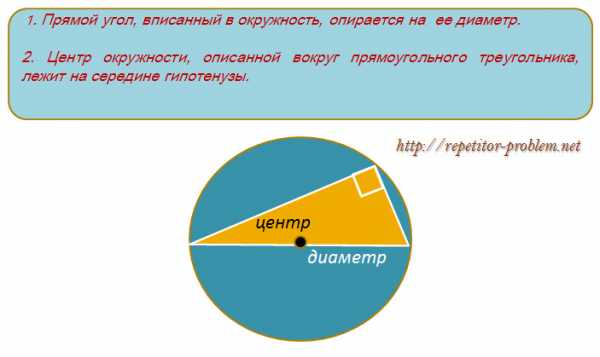
В этом видео демонстрация описанного выше способа.

На самом деле способов, как найти центр окружности существует несколько. Вот как, например, предлагают решить данную задачу авторы сайта “Как Просто!” :

1. Самый простой способ нахождения центра окружности — согнуть лист бумаги, на котором она начерчена, следя на просвет, чтобы окружность оказалась сложена точно пополам. Полученная линия сгиба будет одним из диаметров заданной окружности. Затем лист можно согнуть в другом направлении, получив тем самым второй диаметр. Точка их пересечения и будет центром окружности.

Этот способ, конечно же, годится только для случаев, когда окружность изображена на листе бумаги, бумагу можно сгибать, и есть возможность следить за точностью сгиба на просвет.

2. Предположим, что заданная окружность начерчена на твердом материале, или же это круглая деталь, которую нет возможности согнуть. В этом случае для нахождения ее центра вам понадобится линейка.

Диаметр, по определению этого слова — самый длинный из всех отрезков, которые можно провести между двумя точками одной окружности. Середина любого диаметра окружности совпадает с ее центром.

Наложив линейку на заданную окружность, зафиксируйте нулевую отметку в любой точке окружности. Таким образом вы измерите некоторую секущую, то есть отрезок, соединяющий две точки этой окружности. Затем медленно поворачивайте линейку, следя за изменением ширины отрезка. Она будет возрастать, пока секущая не превратится в диаметр, после чего снова начнет уменьшаться. Отметив момент максимума, вы найдете диаметр, а значит, и центр.

 

Как правило, задачи на окружность не ограничиваются тем, что отвечают на вопрос : “Как найти центр окружности“. Чаще бывает, что нужно найти длину окружности или площадь круга.  

Какие использовать для этого формулы и как их запомнить,  смотрите здесь.

Успехов в учебе!

Татьяна Бурмистренко, автор сайта http://repetitor-problem.net

repetitor-problem.net

Как найти центр круга » VripMaster

Найдя центр круга или окружности, вы сможете решать различные геометрические задачи, например, на вычисление длины окружности или площади круга. Найти центр круга можно разными способами. Вы можете провести пересекающиеся отрезки; вы можете начертить пересекающиеся окружности; вы можете воспользоваться линейками.

Метод 1 из 3: Пересекающиеся отрезки

1. Начертите окружность. Сделайте это при помощи циркуля. Радиус (диаметр) круга может быть любым. Если окружность вам дана, новую окружность чертить не нужно.
   • Циркуль – это инструмент, предназначенный для черчения окружностей и их измерения. Циркуль можно купить в канцелярском магазине или в магазине для школьников.
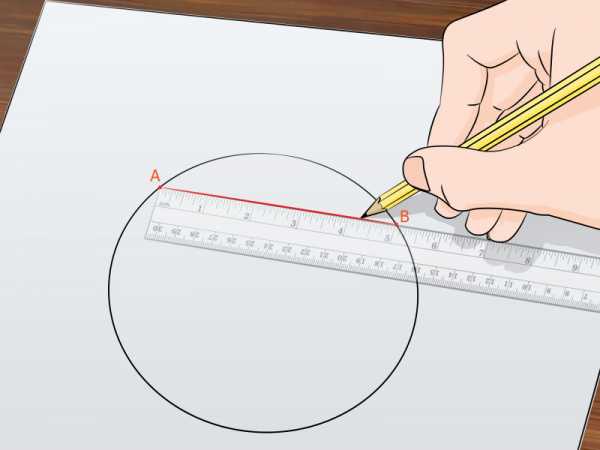2. Проведите хорду. Хорда – это отрезок, соединяющий любые две точки, лежащие на окружности, и не проходящий через центр окружности. Обозначьте эту хорду как АВ.
   • Проводите прямые и отрезки при помощи карандаша, чтобы иметь возможность стереть их после нахождения центра окружности. Не давите на карандаш, чтобы вам было легче стереть нарисованные линии.
3. 

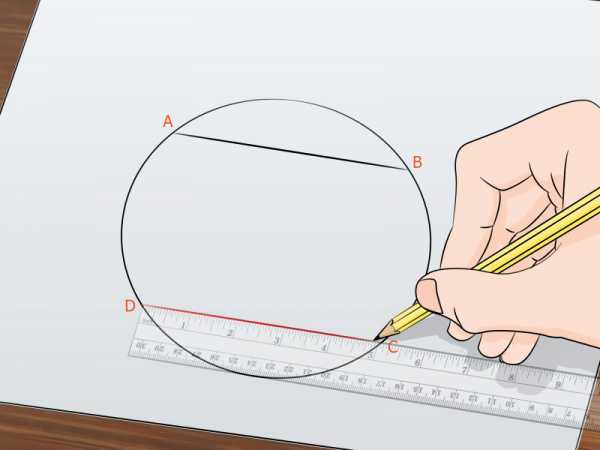
   Проведите вторую хорду. Она должна быть параллельна и равна первой хорде АВ. Обозначьте эту хорду как CD.

4. 

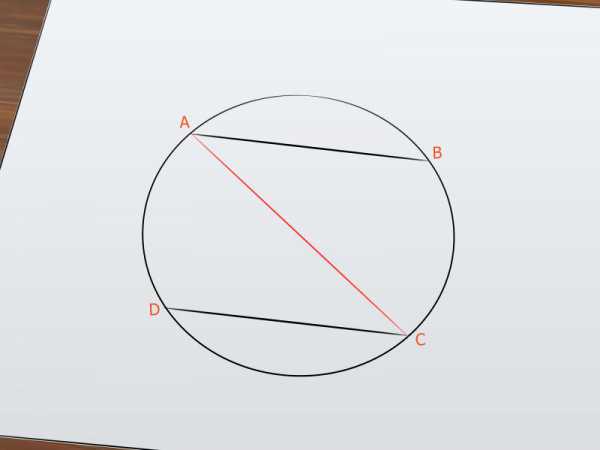
   Соедините точки А и С. Эта третья хорда АС должна проходить через центр окружности, но для его нахождения вам понадобится провести четвертую хорду.

5. 

   Соедините точки B и D. Это четвертая хорда BD, которая должна пересекаться с третьей хордой AC.

6. 

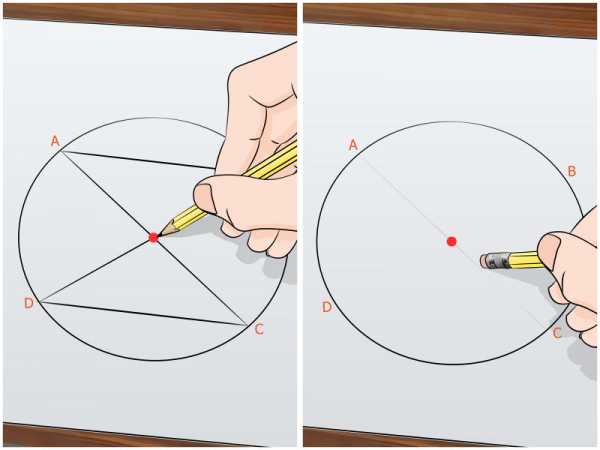
   Найдите центр окружности. Если вы правильно провели все отрезки (хорды), то центр окружности – это точка пересечения хорд AC и BD. Отметьте центр окружности ручкой или карандашом. Если вам нужно отметить только центр окружности, сотрите четыре хорды, которые вы провели ранее.

Метод 2 из 3: Пересекающиеся окружности

1. 

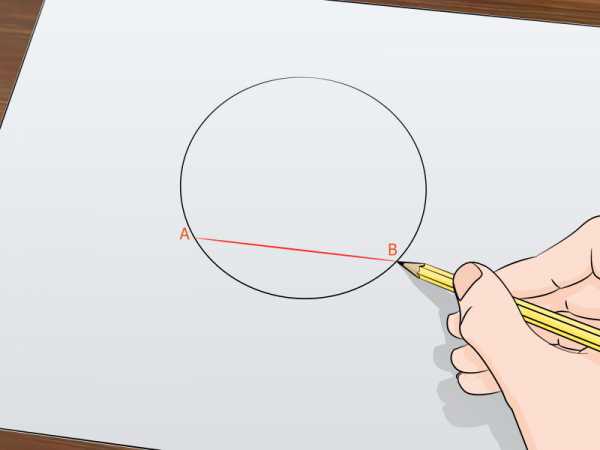
   Между двумя точками окружности проведите хорду. Воспользуйтесь линейкой, чтобы соединить две точки на окружности. Точки можно выбрать произвольно. Обозначьте точки как А и В.

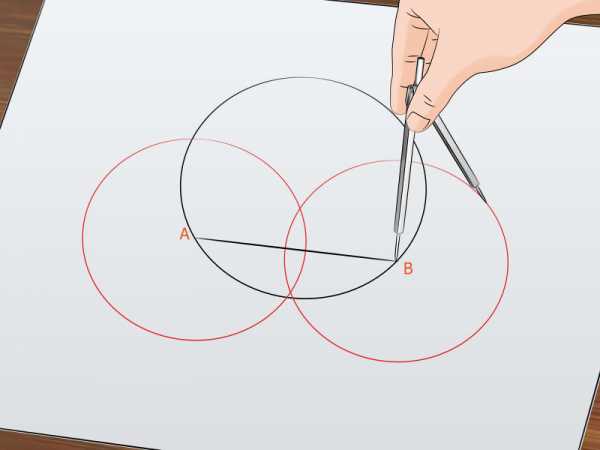2. При помощи циркуля начертите две пересекающиеся окружности. Окружности должны быть одного радиуса. Центром первой окружности сделайте точку А, а второй окружности – точку В. Чертите окружности так, чтобы они пересекались наподобие диаграммы Венна.
   • Чертите окружности карандашом, а не ручкой, чтобы иметь возможность стереть их.
3. 

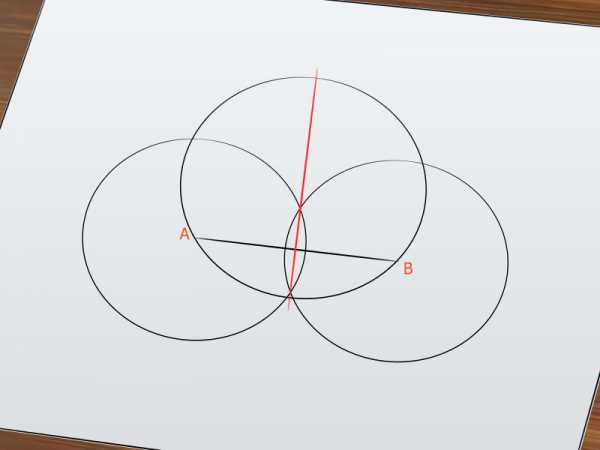
   Проведите вертикальную прямую через точки пересечения начерченных окружностей. Окружности будут пересекаться в двух точках, которые расположены одна над другой. Проведите прямую при помощи линейки; убедитесь, что обе точки лежат на этой прямой. Точки, в которых эта прямая пересекает исходную окружность, обозначьте как С и D. Отрезок СD является диаметром исходной окружности.

4. 

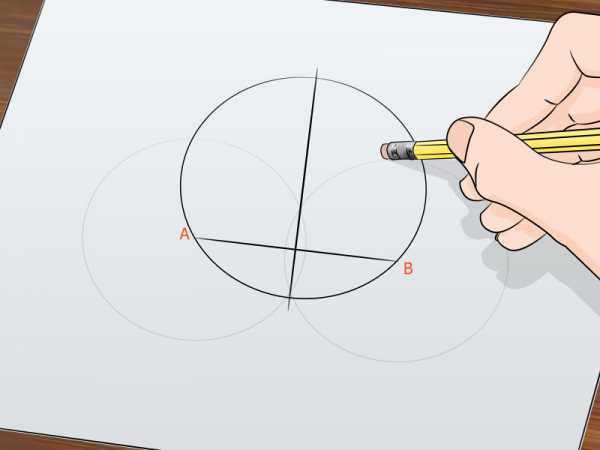
   Сотрите две начерченные вами окружности.

   Это необходимо для того, чтобы очистить пространство для последующих действий. Теперь на вашем листе останется исходная окружность и два перпендикулярных друг другу отрезка. Не стирайте центры стертых окружностей (эти центры расположены в точках А и В). Далее вы начертите две новые окружности.

5. 

   Начертите две новые окружности. Для этого воспользуйтесь циркулем. Центром первой окружности будет точка С, а второй окружности – точка D. Эти окружности также должны пересекаться наподобие диаграммы Венна. Помните, что точки С и D – это точки пересечения вертикальной прямой с исходной окружностью.

6. 

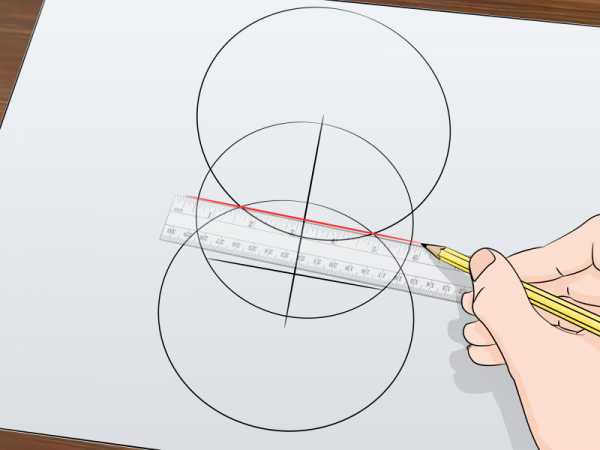
   Проведите прямую через две точки, в которых пересекаются начерченные вами окружности. Эта прямая будет расположена горизонтально. Полученный отрезок представляет собой второй диаметр исходной окружности и должен быть перпендикулярен первому диаметру.

7. 

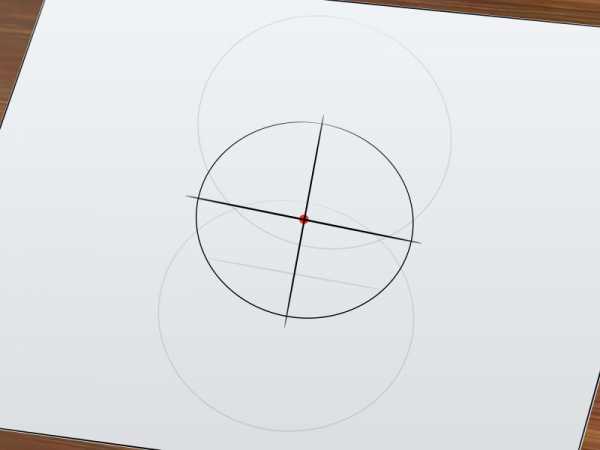
   Найдите центр окружности. Точка пересечения двух диаметров является центром исходной окружности. Отметьте эту точку. Если нужно, сотрите начерченные вами окружности и диаметры.

Метод 3 из 3: Поверочная и треугольная линейки

1. 

   К данной окружности проведите две касательные. Касательные можно провести к двум произвольным точкам окружности. Но вы облегчите себе работу, если проведете касательные под прямым или острым углом друг к другу.

2. 

   Теперь проведите еще две касательные, которые будут параллельны касательным, которые вы провели в предыдущем шаге. Таким образом, проведенные четыре касательные образуют подобие параллелограмма или прямоугольника.

3. 

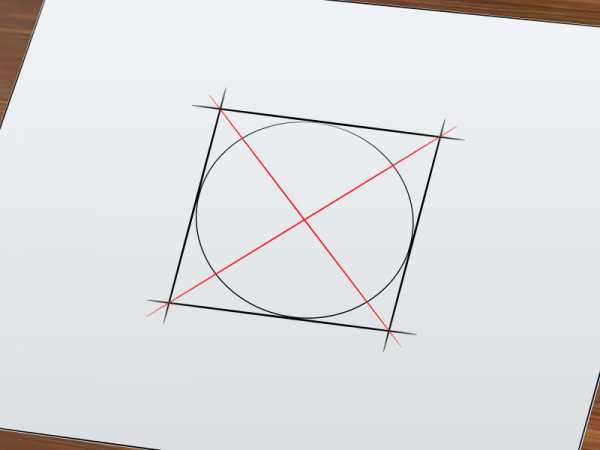
   Проведите диагонали параллелограмма. Точка пересечения этих диагоналей является центром окружности.

4. 

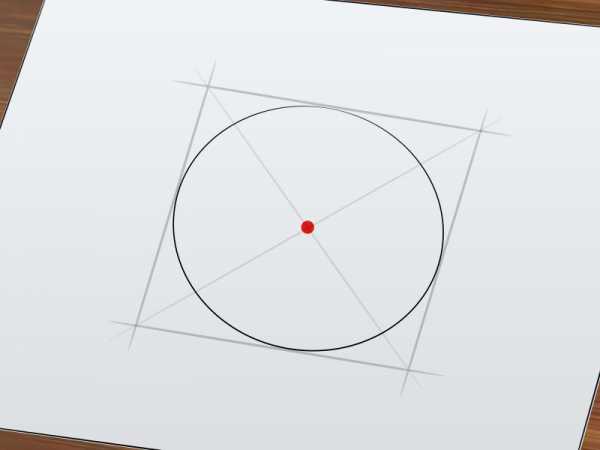
   Проверьте правильность нахождения центра окружности при помощи циркуля. Центр окружности расположен строго в точке пересечения диагоналей, только если вы не допустили ошибку при проведени

vripmaster.com

Как найти центр круга без разметочных инструментов?

  Как найти центр круга без каких либо инструментов?
Легко! Потребуется только карандаш, ножницы и лист бумаги. Не нужна даже линейка!
 Если круг уже готов, а лист бумаги имеет ровные края, то можно обойтись и без ножниц, одним карандашом, но для наглядности будем вырезать и круг, и бумага у нас будет с неровным краем, поэтому воспользуемся ножницами.
    Итак, дано: круг, который нарисовали не по циркулю (там-то сразу центр отмечен иголкой), а путем обведения карандашом какого-то круглого предмета, например, тарелки, блюдца, чашки или какой-то крышки от посуды, упаковки и т.п.

       Возьмем первое, что попалось под руку —  подставку от цветочного горшка, стоящего рядом с компьютером. Там есть, правда, отверстие в центре и можно сразу, взяв иглу или гвоздик, отметить центр. Но мы не будем искать лёгких путей и проигнорируем такую возможность.
     Рисуем на зеленом листе бумаги (взял специально для контраста обложку от тетради) окружность, обведя карандашом нашу подставку.    Вырезаем круг по нарисованной линии. Именно на нём нужно найти центр.
Берем лист бумаги, (подойдет любой, главное, чтобы был подходящим по размеру). В данном случае вполне достаточно тетрадного листочка.  Если круг большой, то можно взять, например, газету большого формата. Принцип всё равно один и тот же: нам будет нужен квадратный лист бумаги, т.е., стороны его должны быть все равны между собой.
  Лист из тетради, как и стандартный лист  писчей бумаги, имеют прямоугольную форму, а не квадратную (газетный лист — аналогично).

 Как сделать его квадратным? — Согнуть с угла на угол так, как показано на фото.
Тот, кто хоть раз в жизни делал бумажный самолетик или какую-то другую игрушку из бумаги, хорошо представляет, как это делается.
    На фото видно, что лист из тетради был вырван неаккуратно, поэтому сгибаем так, чтобы рваные края не задействовать и  после сгибания листа обрезаем их ножницами.  Излишек «прямоугольника» загибаем на противоположную сторону листа и места сгибов хорошенько разглаживаем, чтобы они были хорошо заметны, когда лис снова будет расправлен. Эта линия сгиба и укажет нам диаметр круга, когда мы приложим его так, чтобы края касались двух сторон квадрата. На краях круга делаем отметки карандашом.
Используя подогнутую сторону листа, как линейку (мы договаривались в самом начале, что обходимся без неё)  проводим линию, соединяющую эти метки.
Поворачиваем круг и аналогичным способом намечаем точки для проведения  ещё одного диаметра.
Место пересечения этих линий и будет центром окружности. Для того, чтобы в этом убедиться, мы можем ещё несколько раз повернуть наш круг, каждый раз прикладывая его край к сторонам квадрата и проводя линии через метки сделанные напротив линии сгиба квадрата.
Все они пересекутся в центре окружности, если выполнять работу не спеша и аккуратно.
 Этот принцип можно использовать  в домашней мастерской, когда требуется определить центр какой-либо деревянной заготовки. И для этого легко сделать простейшее самодельное приспособление, которое намного облегчит разметку.

  Есть и совсем простой способ нахождения центра плоской заготовки круглой формы.

Всего-то нужно обвести её по периметру, положив на лист бумаги, затем вырезать по начерченной линии круг, согнуть его вчетверо и центр будет найден. Он находится точно на линии пересечения сгибов.
Остается развернуть листочек, наложить его на заготовку так, чтобы края совпадали в ентре сделать пометку острым предметом, например, шилом.
  

www.instrument-mastera.ru

КАК НАЙТИ В КРУГЕ ЦЕНТР

КАК НАЙТИ В КРУГЕ ЦЕНТР

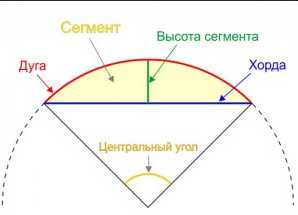
Надо провести хорду, разделить ее пополам и восстановить к ней перпендикуляр, который продолжить до окружности. Эта линия будет диаметр; середина его означит центр. Или взять две хорды, разделить каждую пополам и поставить перпендикуляры: точка их пересечения будет центр крута.

Равные круги имеют равные радиусы, следовательно, и равные диаметры.

КОНЦЕНТРИЧЕСКИЕ КРУГИ

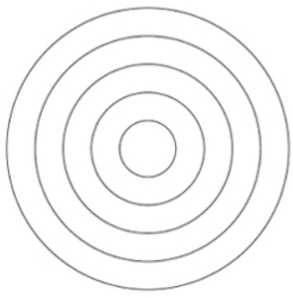
Концентрические круги описываются из одного центра разными радиусами.

ДЕЛЕНИЕ КРУГА ПОПОЛАМ

Круг делится пополам диаметром.

ДЕЛЕНИЕ КРУГА НА ЧЕТЫРЕ РАВНЫЕ ЧАСТИ

Деление круга на четыре равные масти производится проведением двух диаметров под прямыми углами.

ДЕЛЕНИЕ ОКРУЖНОСТИ НА ЗАДАННОЕ ЧИСЛО РАВНЫХ ЧАСТЕЙ

Деление окружности на заданное число равных частей производится делением круга пополам, или на четные части, а потом уже размещать по окружности прочие точки деления, проводя от них для проверки радиусы, которые около центра должны составлять столько же равных углов, насколько делится окружность.

Примечание. Для объяснения — деления круга на части употребляются равные секторы картонного кружка, складываемые вместе. Обучающий дает ученикам заметить, что когда равны дуги, то и углы около центра также раины между собой, и что при уменьшении дуги уменьшается и угол.

Предыдущее правило служит способом для разделения угла на равные части. Из вершины угла, принятой за центр, описывается дуга и разделяется на заданное число частей; потом каждая точка деления соединяется с вершиной угла.

makereality.ru

Как найти середину круга? — Полезная информация для всех

Всех делов тут — вспомнить школьную геометрию. Два радиуса и хорда дают равнобедренный треугольник, в котором высота, опущенная на основание, делит его пополам.

Поэтому на окружности надо отметить три произвольные точки, и одну из них соединить с двумя другими. Это даст две хорды. Теперь делим эти хорды пополам и к каждой проводим перпендикуляр к середине — это стандартная школьная задачка на построение циркулем и линейкой. Точка пересечения перпендикуляров и будет центром круга.

Чтобы найти центр круга, можно отметить 2 любые точки на окружности и провести отрезок.

Затем нужно провести ещ один отрезок, имеющий такую же длину и параллельный первому отрезку.

---

Соединяем противоположные концы отрезков линиями, которые будут параллельными друг другу.

Таким образом, получится прямоугольник, который будет вписан в круг.

Центр пересечения его диагоналей и будет центром нашего круга.

Когда говорят о нахождении центра круга или окружности, то многие считают, что это просто, мол, проведи два диаметра.и вс.А как провести диаметр, если центра не видно.Но с помощью циркуля и простой линейки это сделать возможно.

Отмечаем на окружности(обрамляющей круг) четыре произвольных точки A,B,C,D,примерно располагающих на одном расстоянии друг от друга(это даже не важно).Из точек А и В произвольным радиусом провести засечки циркулем. Две точки А1 и В1-точки пересечения засечек, соединяем, и она точно лежит на диаметре круга.

Аналогично для точек С и Д получим точки С1 и Д1, соединяем их, и прямая С1Д1 тоже лежит на другом диаметре круга.Пересечение любых двух диаметров окружности дат е центр, точку О.

И это один из верных способов построения центра круга и окружности.

Найти середину круга очень просто. Надо нарисовать круг и провести диаметр слева направо и сверху вниз, точка соединения линий и будет середина круга. Если круг уже вырезан, сложить его пополам и еще раз пополам, в точке соединений сгибов и будет середина круга.

Чтобы найти центр круга, достаточно провести диаметр и построить к нему перпендикуляр с помощью циркуля и линейки.

сначала проводим через круг линию (можно произвольно, но лично я для удобства провожу горизонтальную) и с помощью циркуля и линейки проводим перпендикулярную линию, которая делит нашу хорду и весь круг ровно пополам. Аналогично проводим перпендикуляр к уже полученному диаметру и находим центр круга. Ко всему прочему — мы еще разделили окружность на четыре ровные части.

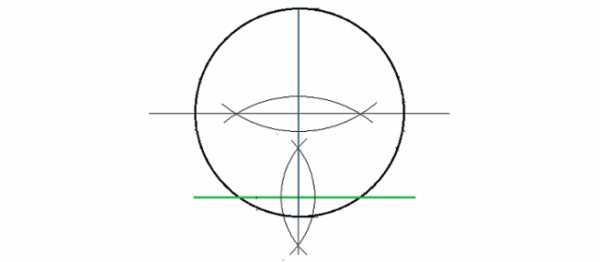
Но бывает, что диаметр провести нельзя, так как есть только часть круга, тогда можно применить способ. который подходит практически везде:

в произвольном месте провести две хорды и через их центры провести перпендикуляры — в точке пересечения и будет центр

Для этого берем треугольник (линейку) и проводим диаметр круга. Далее можно с помощью угольника провести такой же диаметр, перпендикулярный первой линии. Пересечение двух этих линий и будет центром (серединой) круга.

Мне представляется достаточно простой способ нахождения центра окружности путем вписывания в нее прямоугольника. То есть проводим произвольную хорду и принимаем этот отрезок за одну сторону прямоугольника. Достраиваем сперва перпендикулярные стороны из точек пересечения хорды с окружностью, потом достраиваем противоположную параллельную сторону. Вся проблема — в проведении перпендикуляров, но и во всех остальных методах применяется тот же принцип построения. После получения такого прямоугольника проводим в нем диагонали и вуаля, точка их пересечения и будет центром окружности, ну а сами диагонали окажутся диаметрами.

Очень просто — измеряем диаметр круга, строим вокруг нашей окружности равносторонний квадрат, со сторонами равными диаметру круга. Стороны квадрата пройдут по касательной к окружности. Далее делим этот квадрат по диагонали на четыре треугольника. В точке пересечения линий будет цент круга.

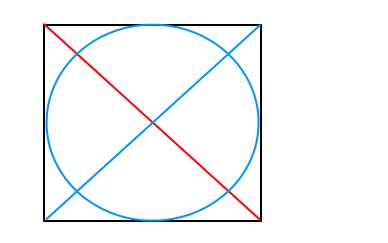
Чтобы найти середину круга нужно провести две хорды. У каждой из них найти середины и провести к ним перпендикулярные лучи. Точка пересечения этих лучей и будет центром круга.

Также центр круга можно найти при помощи циркуля. Для этого нужно провести горизонтальную линию от одной точки окружности до другой (отмечаем точки А и В):

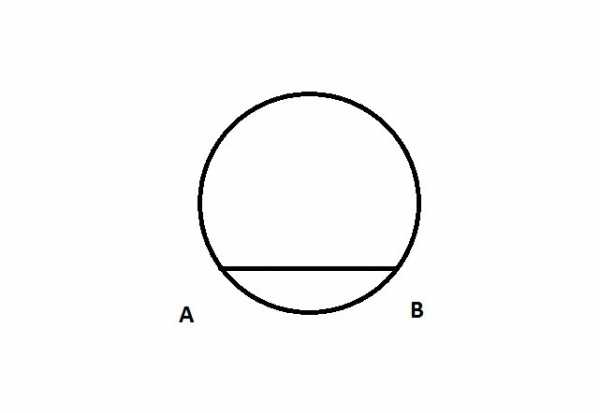
При помощи циркуля начертить два одинаковых перекрывающихся круга с центрами в точках А и В.

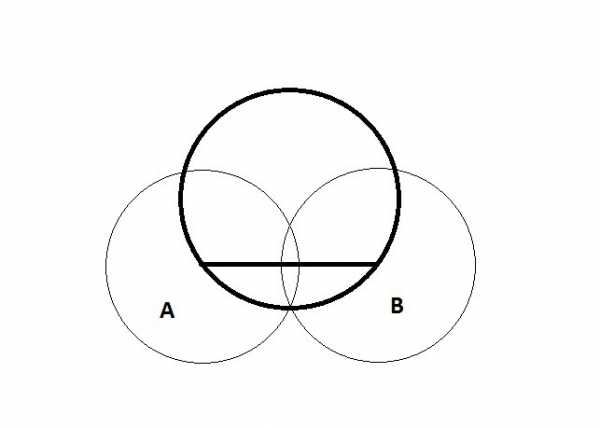
Далее проводим вертикальную линию через точку, в которой круги пересекаются. Отмечаем на окружности точки C и D:

Для удобства стираем два вспомогательных круга и получаем такой рисунок:

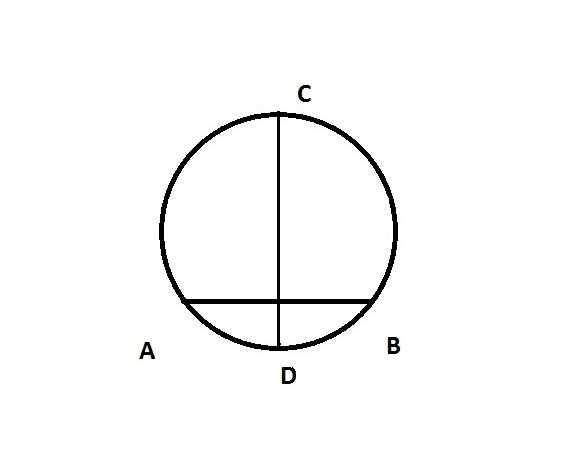
Чертим ещ два одинаковых перекрывающихся круга с центрами в точках С и D:

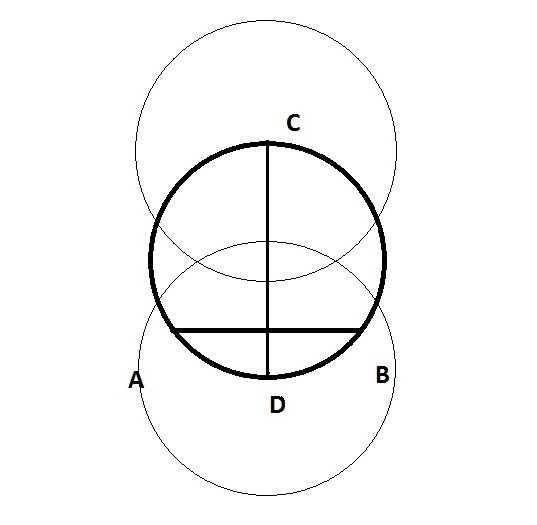
Проводим горизонтальную линию через точки пересечения этих двух кругов. Отмечаем на окружности точки Е и F:

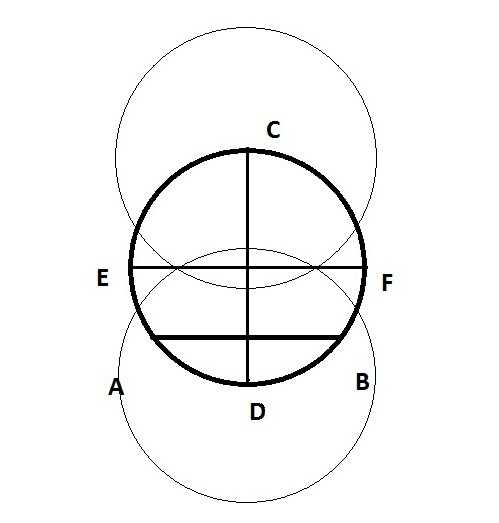
Стираем вспомогательные круги. Точка пересечения прямых СD и EF (назовм е точкой О) и будет искомой серединой круга.

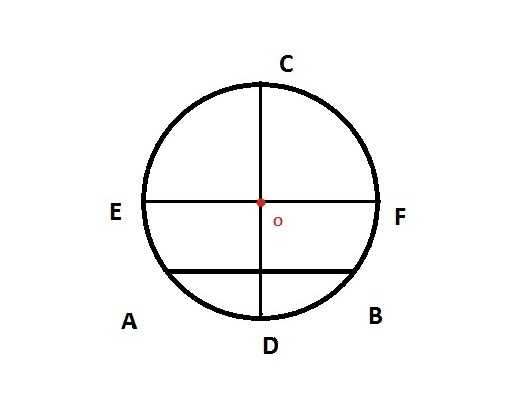
info-4all.ru

Как найти центр окружности | Сделай все сам

Часто столярам и плотникам в работе требуется геометрия. Один из самых блестящих примеров — построение верной окружности. Еще одна задача, с которой в данном случае дозволено столкнуться — это определение центра круга, не прибегая к особым инструментам и трудным вычислениям.

Вам понадобится

• Линейка и карандаш

Инструкция

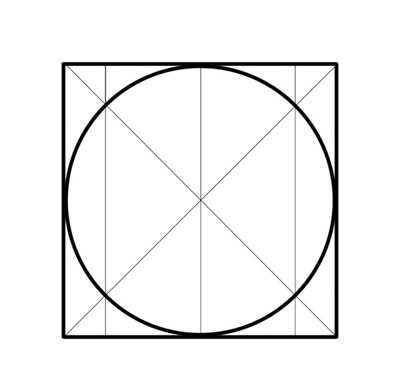
1. Для того дабы обнаружить центр окружности, нужно вначале вписать ее в квадрат. То есть все стороны четырехугольника обязаны касаться круга. Для этого проведите с подмогой линейки четыре ровные линии.

2. Сейчас объедините по диагонали два противоположных угла. Следите за тем, дабы линия разбивала угол квадрата на две равные части. Объедините прямыми все 4 угла квадрата.

3. Точка пересечения данных прямых и будет центром окружности.

4. Еще одной фигурой, которая может подмогнуть определить центр круга, является прямоугольный треугольник. Его также надобно вписать в окружность. А после этого поделить противоположную прямому углу сторону напополам. Середина гипотенузы и будет центром окружности.

В силу определенных причин изредка надобно поделить круг на равные части, но не неизменно имеются нужные навыки и знания, дабы это осуществить. А чай сделать это дозволено различными методами, всякий из которых по-своему практичен и комфортен.

Вам понадобится

• Бумага, линейка, транспортир, карандаш, ножницы.

Инструкция

1. Дозволено пойти особенно простым путем, то есть сделать копию надобной фигуры, вырезать ее и после этого путем сгибания поделить на нужное число секций. Впрочем тут необходимо рассматривать, что таким образом, складывая круг напополам, дозволено его поделить на 2 части. Сложив фигуру еще раз, получим 4 части. Продолжая складывать круг , в итоге будет 8, а после этого 16 частей. После этого дозволено приложить вырезанный круг к основному и подметить в местах заломов секции на стержневой требуемой фигуре.

2. Впрочем при делении круг а таким методом не получается 3, 5, 7, 9 либо 11 частей. В этих случаях придется воспользоваться транспортиром. Если нет вероятности определить середину круг а, то вновь вначале надобно обвести фигуру, вырезать ее и сложить в два, а после этого в четыре раза. Перпендикулярные линии на пересечении дадут точку, которая показывает середину. От нее нужно проводить все отметки.

3. Каждый круг составляет 360°, следственно, дозволено посчитать градусы всякого числа частей. Скажем, надобно сделать 5 секций. Для этого 360° поделите на 5 частей — получается 72°. То есть, всякий секция будет составлять 72°. Поставьте транспортир, тот, что охватывает 180° на середину и отмерьте 72°. Проведите линию от центральной серединной точки до отмеренного градуса, после этого исполните то же самое еще 3 раза. В результате получится 5 равных частей круг а.

4. Если нужно поделить круг , скажем, на 12 частей, то для этого путем складывания рабочего круг а, поделите его на 4 части. На центральную точку положите транспортир. Если 360° поделить на 12, получится 30°. То есть каждого будет 12 частей по 30°. Таким образом, вследствие транспортиру дозволено поделить круг дословно на всякое число равных частей.

Центр фигуры дозволено обнаружить несколькими методами, смотря какие данные о ней теснее вестимы. Стоит разобрать нахождение центра окружности, которая является общностью точек, располагающихся на равном расстоянии от центра, потому что эта фигура — одна из особенно распространенных.

Вам понадобится

• — угольник;
• — линейка.

Инструкция

1. Примитивный метод обнаружить центр окружности – согнуть лист бумаги, на котором она начерчена, удостоверясь, глядя на просвет, что она сложилась верно напополам. После этого согните лист перпендикулярно первому сгибу. Так вы получите диаметры, точка пересечения которых и есть центр фигуры.

2. Финально, данный метод совершенен, только если окружность начерчена на бумаге, довольно тонкой, дабы дозволено было посмотреть на просвет, верно ли труден лист.

3. Возможен, рассматриваемую фигуру начертили на твердой, несгибаемой поверхности либо это отдельная деталь, которая также не поддается сгибу. Дабы обнаружить центр окружности в этом случае, вам надобна линейка.

4. Диаметр является самым длинным отрезком, соединяющим 2 точки окружности. Как вестимо, проходит он через центр, следственно задача нахождения центра окружности сводится к нахождению диаметра и его середины.

5. Наложите линейку на окружность, позже чего зафиксируйте в всякий точке фигуры нулевую отметку. Приложите линейку к окружности, получив секущую, а после этого двигайте по направлению к центру фигуры. Длина секущей будет вырастать, пока не дойдет до пиковой точки. Вы получите диаметр, а обнаружив его середину, обнаружите и центр окружности.

6. Центр описанной окружности для всякого треугольника располагается на пересечении срединных перпендикуляров. В случае, если треугольник прямоугольный, ее центр неизменно будет совпадать с серединой гипотенузы. То есть решение кроется в построении внутри окружности прямоугольного треугольника с вершинами, лежащими на окружности.

7. Трафаретом для прямого угла могут послужить школьный либо строительный угольник, линейка либо даже лист бумаги/картона. Разместите в всякую точку окружности вершину прямого угла, сделайте отметки в тех местах, где стороны угла пересекают рубеж окружности, объедините их. У вас получился диаметр – гипотенуза.

8. Таким же методом обнаружьте еще один диаметр, место пересечения 2-х таких отрезков и будет центром окружности.

Видео по теме

Обратите внимание!
Квадрат, вблизи которого описана окружность, должен быть построен по правилам. Нужно, дабы все стороны четырехугольника были равны, а радиус углов составлял 90 градусов.

jprosto.ru