Параллелограмм. Свойства и признаки параллелограмма
Определение параллелограмма
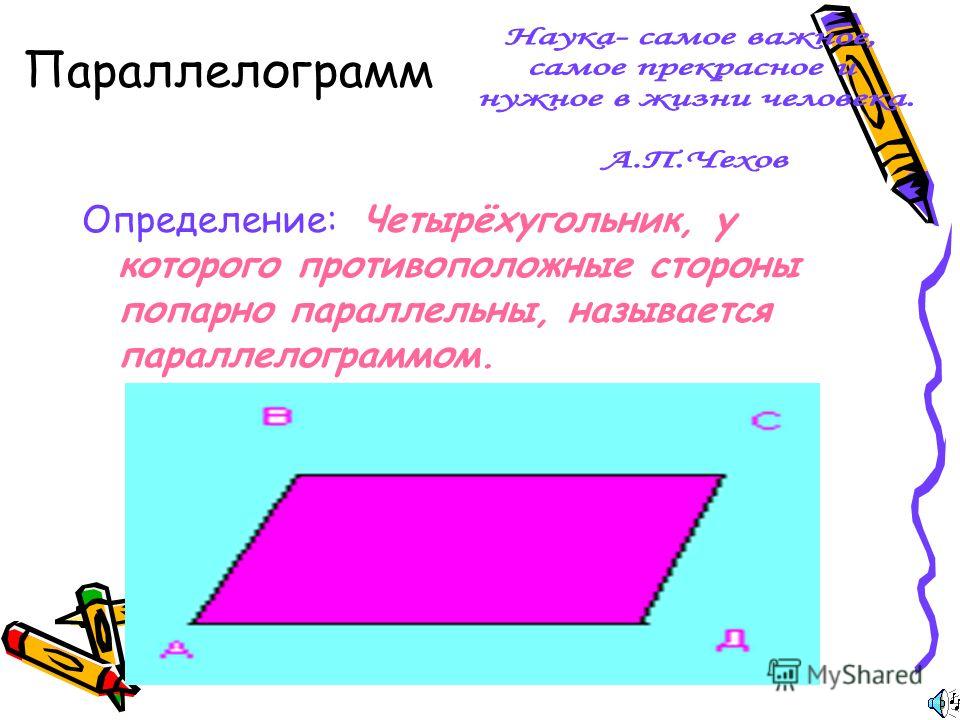
Параллелограмм – четырехугольник, у которого противоположные стороны попарно параллельны.
Частные случаи параллелограмма: ромб, прямоугольник, квадрат.
Свойства параллелограмма
1. Противоположные стороны параллелограмма попарно равны
2. Противоположные углы параллелограмма попарно равны
3. Сумма смежных (соседних) углов параллелограмма равна 180 градусов
4. Сумма всех углов равна 360°
5. Диагонали параллелограмма пересекаются и точкой пересечения делятся пополам
6. Точка пересечения диагоналей является центром симметрии параллелограмма
7.
связаны следующим соотношением:
8. Биссектриса отсекает от параллелограмма равнобедренный треугольник
Признаки параллелограмма
Четырехугольник является параллелограммом, если выполняется хотя бы одно из следующих условий:
1. Противоположные стороны попарно равны:
2. Противоположные углы попарно равны:
3. Диагонали пересекаются и в точке пересечения делятся пополам
4. Противоположные стороны равны и параллельны:
5.
Небольшой видеоролик о свойствах параллелограмма (в том числе ромба, прямоугольника, квадрата) и о том, как эти свойства применяются в задачах:
Формулы площади параллелограмма смотрите здесь.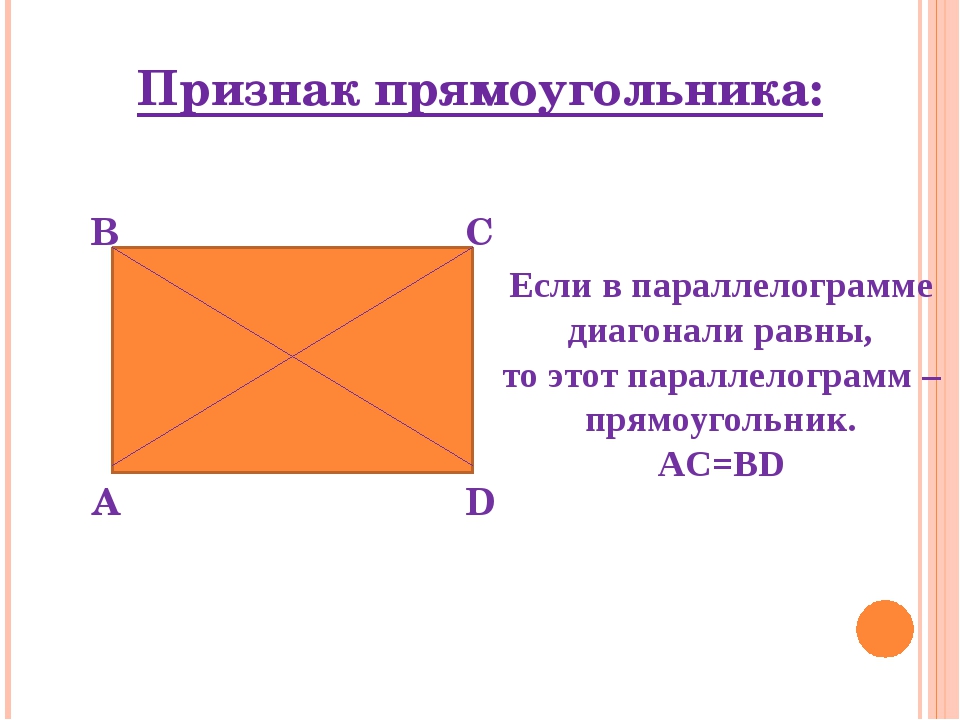
Хорошую подборку задач на нахождение углов и длин в параллелограмме смотрите здесь.
Развертка Прямоугольного Параллелепипеда. Определение, пример.
Определение параллелепипеда
Параллелепипед — это многогранник, у которого шесть граней.
У параллелепипеда каждая грань представляют собой параллелограмм, противоположные грани которого равны.
Прямоугольный параллелепипед — это многогранник с шестью гранями, каждая из которых является прямоугольником.
Свойства прямоугольного параллелепипеда
|
Диагональ прямоугольного параллелепипеда — это отрезок, который соединяет две противоположные вершины. Все диагонали равны, пересекаются в одной точке и делятся ею пополам.
Схема создания прямоугольного параллелепипеда
Для сборки параллелепипеда нужно распечатать развертку на обычном листе формата А4. Для печати можно использовать белую или цветную бумагу.
Как сделать развертку прямоугольного параллелепипеда:
- Согнуть по обозначенным линиям вырезанную развертку параллелепипеда:
- Обратить внимание на последовательность склеивания на лепестках.
Приклеить центральный лепесток. Вот, что должно получиться: - Приклеить детали в месте склеивания №2 и №3. Вот так:
- Получилась готовая модель прямоугольного параллелепипеда.
Развертка прямоугольного параллелепипеда с размерами
Геометрические размеры параллелепипеда №1:
- Длина = 120 мм
- Ширина = 90 мм
- Высота = 40 мм
Прямоугольный параллелепипед с такими размерами выглядит так:
Геометрические размеры параллелепипеда №2:
- Длина = 90 мм
- Ширина = 65 мм
- Высота = 50 мм
Прямоугольный параллелепипед с такими размерами выглядит так:
Геометрические размеры параллелепипеда №3:
- Длина = 60 мм
- Ширина = 40 мм
- Высота = 65 мм
Прямоугольный параллелепипед с такими размерами выглядит так:
Так выглядит соотношение размеров параллелепипедов для представленных разверток:
Развертка может пригодиться, если нужно сделать прямоугольный параллелепипед из бумаги или картона на уроке математики в 5 классе.
Также развертка помогает решать некоторые задачи. Например, находить кратчайшее расстояние между точками на поверхности геометрического тела.
Планиметрия (Геометрия на плоскости) — Математика — Теория, тесты, формулы и задачи
Оглавление:
Основные теоретические сведения
Треугольник
К оглавлению…
При решении задач по геометрии помимо всех геометрических формул и свойств, которые будут приведены ниже, нужно очень хорошо помнить основные формулы по тригонометрии. Укажем для начала несколько основных свойств различных типов углов:
- Смежные углы в сумме равны 180 градусов.
- Вертикальные углы равны между собой.
Теперь перейдем к свойствам треугольника. Пусть имеется произвольный треугольник:
Тогда, сумма углов треугольника:
Запомните также, что сумма любых двух сторон треугольника всегда больше третьей стороны. Площадь треугольника через две стороны и угол между ними:
Площадь треугольника через две стороны и угол между ними:
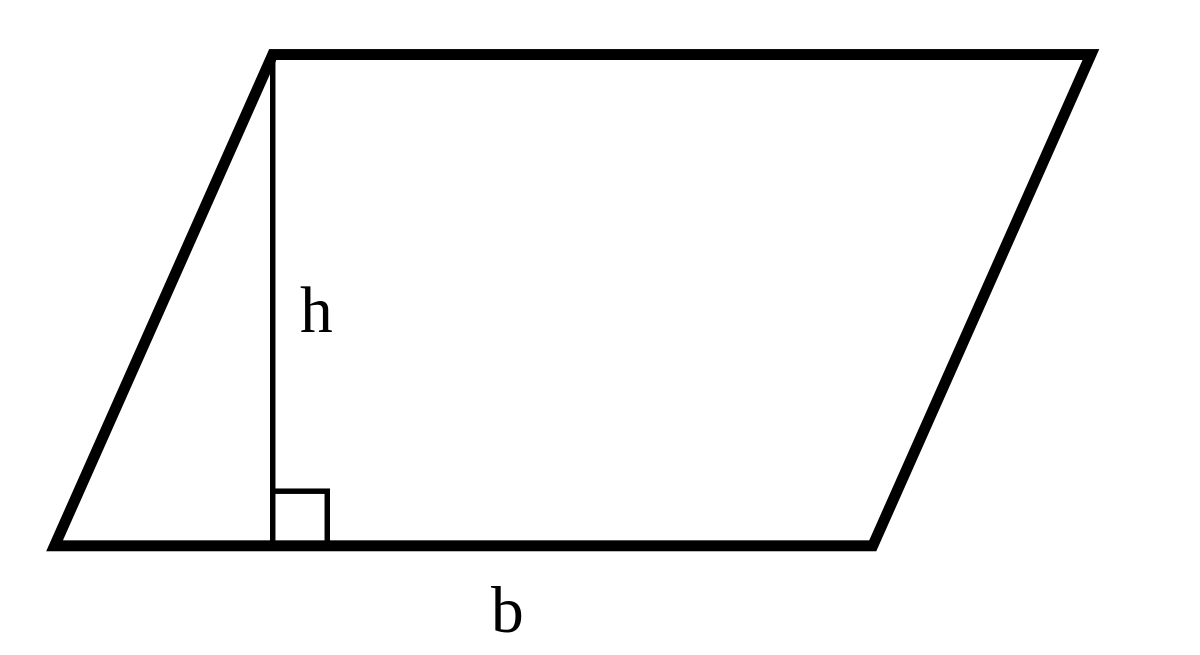
Площадь треугольника через сторону и высоту опущенную на неё:
Полупериметр треугольника находится по следующей формуле:
Формула Герона для площади треугольника:
Площадь треугольника через радиус описанной окружности:
Формула медианы (медиана — линия проведенная через некоторую вершину и середину противоположной стороны в треугольнике):
Свойства медиан:
- Все три медианы пересекаются в одной точке.
- Медианы делят треугольник на шесть треугольников одинаковой площади.
- В точке пересечения медианы делятся в отношении 2:1, считая от вершин.
Свойство биссектрисы (биссектриса — линия, которая делит некоторый угол на два равных угла, т.е. пополам):
Важно знать: Центр вписанной в треугольник окружности лежит на пересечении биссектрис (все три биссектрисы пересекаются в этой одной точке). Формулы биссектрисы:
Формулы биссектрисы:
Основное свойство высот треугольника (высота в треугольнике — линия проходящая через некоторую вершину треугольника перпендикулярно противоположной стороне):
Все три высоты в треугольнике пересекаются в одной точке. Положение точки пересечения определяется типом треугольника:
- Если треугольник остроугольный, то точка пересечения высот находится внутри треугольника.
- В прямоугольном треугольнике высоты пересекаются в вершине прямого угла.
- Если треугольник тупоугольный, то точка пересечения высот находится за пределами треугольника.
Формула высоты:
Еще одно полезное свойство высот треугольника:
Теорема косинусов:
Теорема синусов:
Центр окружности описанной около треугольника лежит на пересечении посерединных перпендикуляров. Все три посерединных перпендикуляра пересекаются в одной этой точке.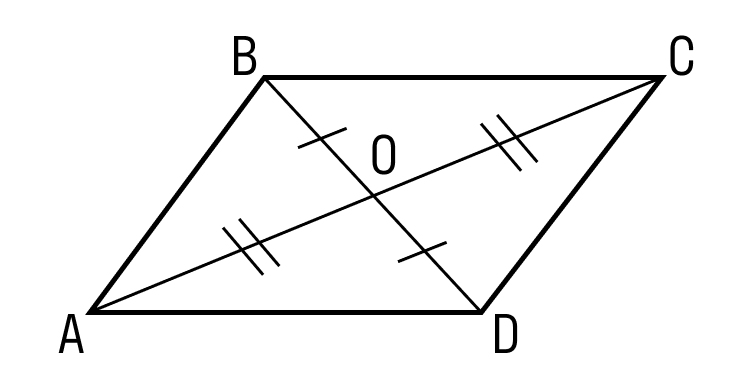 Посерединный перпендикуляр — линия проведенная через середину стороны треугольника перпендикулярно ей.
Посерединный перпендикуляр — линия проведенная через середину стороны треугольника перпендикулярно ей.
Радиус окружности, вписанной в правильный треугольник:
Радиус окружности, описанной около правильного треугольника:
Площадь правильного треугольника:
Теорема Пифагора для прямоугольного треугольника (c — гипотенуза, a и b — катеты):
Радиус окружности, вписанной в прямоугольный треугольник:
Радиус окружности, описанной вокруг прямоугольного треугольника:
Площадь прямоугольного треугольника (h — высота опущенная на гипотенузу):
Свойства высоты, опущенной на гипотенузу прямоугольного треугольника:
Подобные треугольники — треугольники, у которых углы соответственно равны, а стороны одного пропорциональны сходственным сторонам другого. В подобных треугольниках соответствующие линии (высоты, медианы, биссектрисы и т. п.) пропорциональны. Сходственные стороны подобных треугольников — стороны, лежащие напротив равных углов. Коэффициент подобия — число k, равное отношению сходственных сторон подобных треугольников. Отношение периметров подобных треугольников равно коэффициенту подобия. Отношение длин биссектрис, медиан, высот и серединных перпендикуляров равно коэффициенту подобия. Отношение площадей подобных треугольников равно квадрату коэффициента подобия.
п.) пропорциональны. Сходственные стороны подобных треугольников — стороны, лежащие напротив равных углов. Коэффициент подобия — число k, равное отношению сходственных сторон подобных треугольников. Отношение периметров подобных треугольников равно коэффициенту подобия. Отношение длин биссектрис, медиан, высот и серединных перпендикуляров равно коэффициенту подобия. Отношение площадей подобных треугольников равно квадрату коэффициента подобия.
- По двум углам. Если два угла одного треугольника соответственно равны двум углам другого, то треугольники подобны.
- По двум сторонам и углу между ними. Если две стороны одного треугольника пропорциональны двум сторонам другого и углы между этими сторонами равны, то треугольники подобны.
- По трём сторонам. Если три стороны одного треугольника пропорциональны трем сходственным сторонам другого, то треугольники подобны.
Трапеция
К оглавлению. ..
..
Трапеция — четырёхугольник, у которого ровно одна пара противолежащих сторон параллельна. Длина средней линии трапеции:
Площадь трапеции:
Некоторые свойства трапеций:
- Средняя линия трапеции параллельна основаниям.
- Отрезок, соединяющий середины диагоналей трапеции, равен полуразности оснований.
- В трапеции середины оснований, точка пересечения диагоналей и точка пересечения продолжений боковых сторон находятся на одной прямой.
- Диагонали трапеции разбивают её на четыре треугольника. Треугольники, сторонами которых являются основания — подобны, а треугольники, сторонами которых являются боковые стороны — равновелики.
- Если сумма углов при любом основании трапеции равна 90 градусов, то отрезок соединяющий середины оснований равен полуразности оснований.
- У равнобедренной трапеции углы при любом основании равны.
- У равнобедренной трапеции диагонали равны.

- В равнобедренной трапеции высота, опущенная из вершины на большее основание, делит его на два отрезка, один из которых равен полусумме оснований, другой — полуразности оснований.
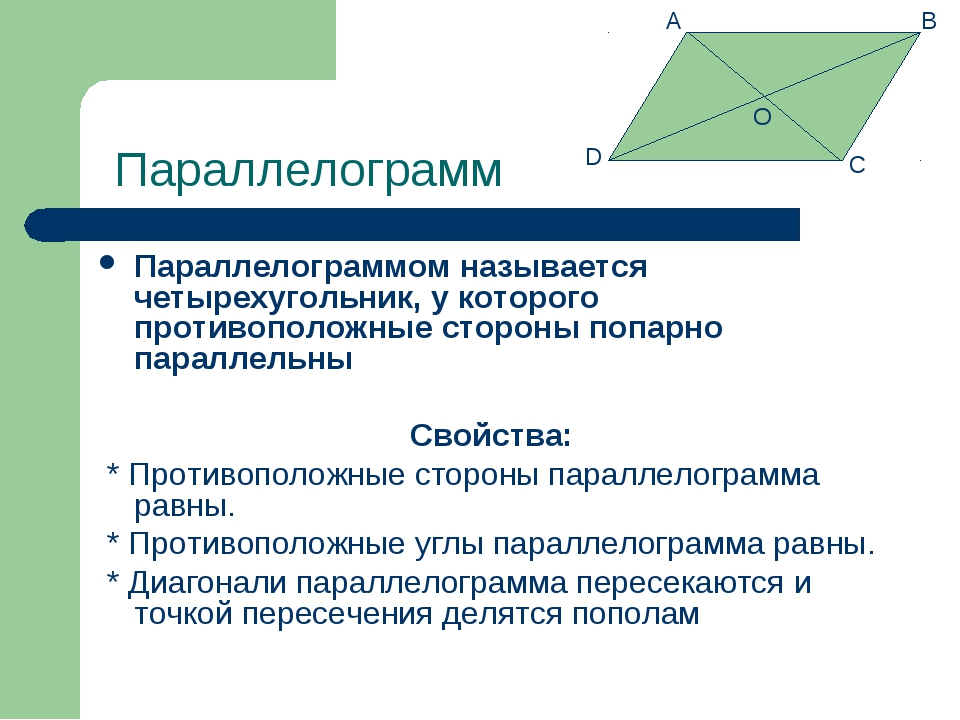
Параллелограмм
К оглавлению…
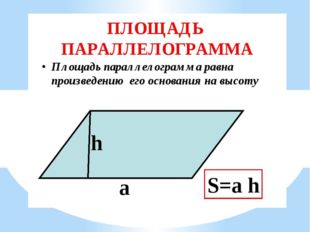
Параллелограмм — это четырёхугольник, у которого противолежащие стороны попарно параллельны, то есть лежат на параллельных прямых. Площадь параллелограмма через сторону и высоту опущенную на неё:
Площадь параллелограмма через две стороны и угол между ними:
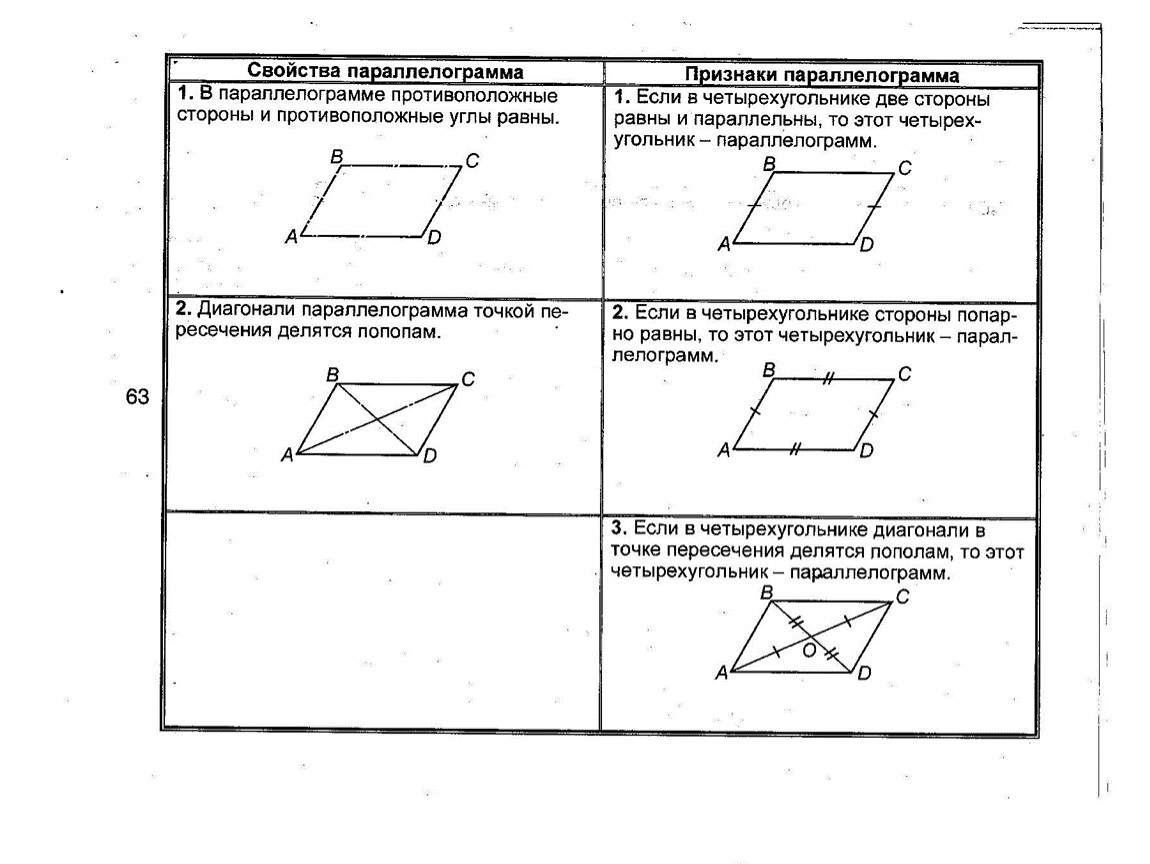
Некоторые свойства параллелограмма:
- Противоположные стороны параллелограмма равны.
- Противоположные углы параллелограмма равны.
- Диагонали параллелограмма пересекаются и точкой пересечения делятся пополам.
- Сумма углов, прилежащих к одной стороне, равна 180 градусов.
- Сумма всех углов параллелограмма равна 360 градусов.
- Сумма квадратов диагоналей параллелограмма равна удвоенной сумме квадратов его сторон.
Квадрат
К оглавлению…
Квадрат — четырёхугольник, у которого все стороны равны, а все углы равны по 90 градусов. Площадь квадрата через длину его стороны:
Площадь квадрата через длину его диагонали:
Свойства квадрата – это все свойства параллелограмма, ромба и прямоугольника одновременно.
Ромб и прямоугольник
К оглавлению…
Ромб — это параллелограмм, у которого все стороны равны. Площадь ромба (первая формула — через две диагонали, вторая — через длину стороны и угол между сторонами):
Свойства ромба:
- Ромб является параллелограммом. Его противолежащие стороны попарно параллельны.
- Диагонали ромба пересекаются под прямым углом и в точке пересечения делятся пополам.
- Диагонали ромба являются биссектрисами его углов.
Прямоугольник — это параллелограмм, у которого все углы прямые (равны 90 градусам). Площадь прямоугольника через две смежные стороны:
Площадь прямоугольника через две смежные стороны:
Свойства прямоугольника:
- Диагонали прямоугольника равны.
- Прямоугольник является параллелограммом — его противоположные стороны параллельны.
- Стороны прямоугольника являются одновременно его высотами.
- Квадрат диагонали прямоугольника равен сумме квадратов двух его не противоположных сторон (по теореме Пифагора).
- Около любого прямоугольника можно описать окружность, причем диагональ прямоугольника равна диаметру описанной окружности.
Произвольные фигуры
К оглавлению…
Площадь произвольного выпуклого четырёхугольника через две диагонали и угол между ними:
Связь площади произвольной фигуры, её полупериметра и радиуса вписанной окружности (очевидно, что формула выполняется только для фигур в которые можно вписать окружность, т.е. в том числе для любых треугольников):
Обобщённая теорема Фалеса: Параллельные прямые отсекают на секущих пропорциональные отрезки.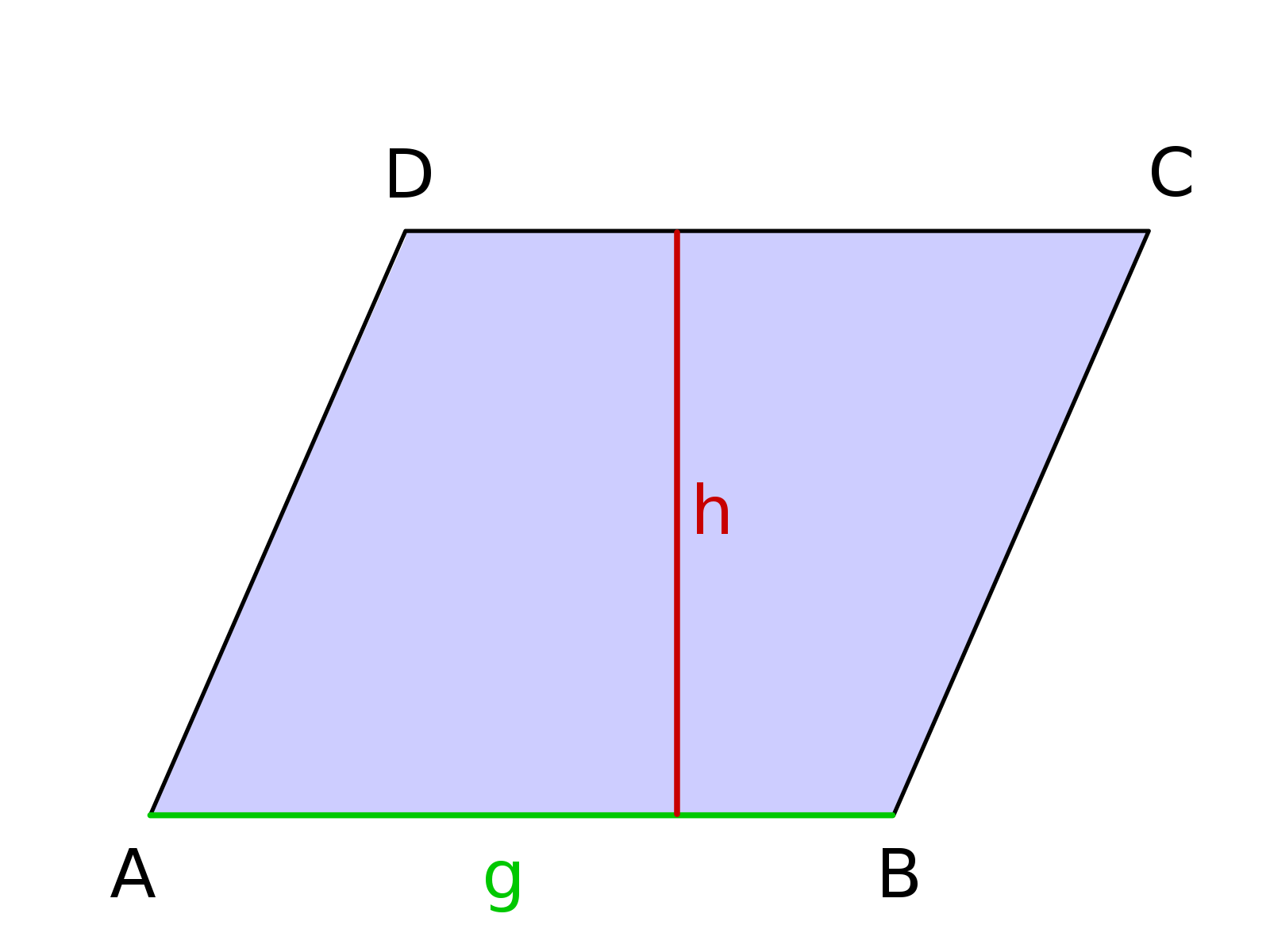
Условие, при выполнении которого возможно вписать окружность в четырёхугольник:
Условие, при выполнении которого возможно описать окружность вокруг четырёхугольника:
Многоугольники
К оглавлению…
Выпуклым многоугольником называется многоугольник, обладающий тем свойством, что все его точки лежат по одну сторону от любой прямой, проходящей через две его соседние вершины. Сумма внутренних углов плоского выпуклого n-угольника равна:
Число диагоналей всякого многоугольника равно (где: n – число сторон):
Правильный многоугольник – это выпуклый многоугольник, у которого все стороны между собой равны и все углы между собой равны. Внутренний угол правильного многоугольника равен:
Центральный угол правильного n-угольника равен:
Площадь правильного многоугольника с числом сторон n, длиной стороны a, радиусом описанной окружности R, полупериметром p и радиусом вписанной окружности r, может быть рассчитана по следующим формулам:
Окружность
К оглавлению. ..
..
Свойство касательных:
Свойство хорды:
Теорема о пропорциональных отрезках хорд:
Теорема о касательной и секущей:
Теорема о двух секущих:
Теорема о центральном и вписанном углах (величина центрального угла в два раза больше величины вписанного угла, если они опираются на общую дугу):
Свойство вписанных углов (все вписанные углы опирающиеся на общую дугу равны между собой):
Свойство центральных углов и хорд:
Свойство центральных углов и секущих:
Длина окружности:
Длина дуги окружности:
Площадь круга:
Площадь сектора:
Площадь кольца:
Площадь кругового сегмента:
Танграм своими руками (схемы игры, фигуры)
Танграм — старинная восточная головоломка из фигур, получившихся при разрезании квадрата на 7 частей особым образом: 2 больших треугольника, один средний, 2 маленьких треугольника, квадрат и параллелограмм.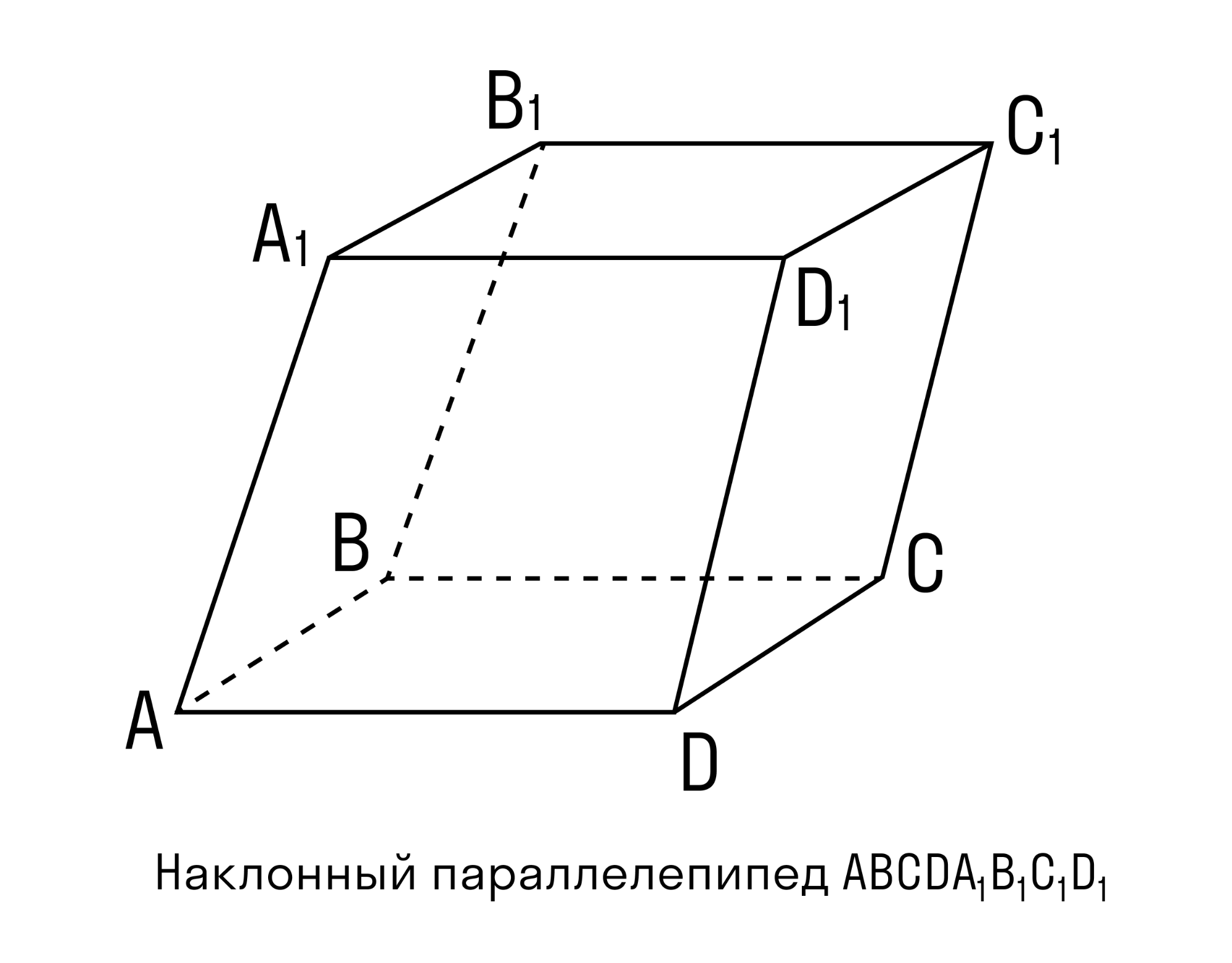 В результате складывания этих частей друг с другом получаются плоские фигуры, контуры которых напоминают всевозможные предметы, начиная от человека, животных и заканчивая орудиями труда и предметами обихода. Такого рода головоломки часто называют «геометрическими конструкторами», «головоломками из картона» или «разрезными головоломками».
В результате складывания этих частей друг с другом получаются плоские фигуры, контуры которых напоминают всевозможные предметы, начиная от человека, животных и заканчивая орудиями труда и предметами обихода. Такого рода головоломки часто называют «геометрическими конструкторами», «головоломками из картона» или «разрезными головоломками».
С танграмом ребенок научится анализировать изображения, выделять в них геометрические фигуры, научится визуально разбивать целый объект на части, и наоборот — составлять из элементов заданную модель, а самое главное — логически мыслить.
Как сделать танграм
Танграм можно сделать из картона или бумаги, распечатав шаблон и разрезав по линиям. Вы можете скачать и распечатать схему квадрата танграма, кликнув по картинке и выбрав «печать» или «сохранить картинку как…».
Можно и без шаблона. В квадрате чертим диагональ — получается 2 треугольника. Один из них разрезаем пополам на 2 небольших треугольника. Отмечаем на каждой стороне второго большого треугольника середину. Отсекаем по этим отметкам средний треугольник и остальные фигуры. Есть и другие варианты, как расчертить танграм, но когда вы его разрежете на части, они будут абсолютно те же самые.
Отсекаем по этим отметкам средний треугольник и остальные фигуры. Есть и другие варианты, как расчертить танграм, но когда вы его разрежете на части, они будут абсолютно те же самые.
Более практичный и долговечный танграм можно вырезать из жесткой офисной папки или пластиковой коробки из под DVD. Можно немного усложнить себе задачу, вырезав танграм из кусочков разного фетра, обметав их по краям, или вовсе из фанеры или дерева.
Как играть в танграм
Каждая фигура игры должна складываться из семи частей танграма, и при этом они не должны перекрываться.
Самый легкий вариант для детей дошкольников 4-5 лет — собирать фигуры по расчерченным на элементы схемам (ответам), как мозаику. Немного практики, и ребенок научится составлять фигуры по образцу-контуру и даже придумывать свои фигуры по такому же принципу.
Уровень первый — скачать и распечатать цветной танграм, так легче будет ориентироваться в схеме.
Схемы и фигуры игры танграм
В последнее время танграм частенько используют дизайнеры. Самое удачное применение танграма, пожалуй, в качестве мебели. Есть и столы-танграмы, и трансформируемая мягкая мебель, и корпусная мебель. Вся мебель, построенная по принципу танграма, довольно удобна и функциональна. Она может видоизменятся в зависимости от настроения и желания хозяина. Сколько всевозможных вариантов и комбинаций можно составить из треугольных, квадратных и четырехугольных полок. При покупке такой мебели вместе с инструкцией покупателю выдаются несколько листов с картинками на разные темы, которые можно сложить из этих полок. В гостиной можно повесить полки в виде людей, в детской из этих же полок можно сложить котов, зайцев и птиц, а в столовой или библиотеке — рисунок может быть на строительную тему — дома, замки, храмы.
Самое удачное применение танграма, пожалуй, в качестве мебели. Есть и столы-танграмы, и трансформируемая мягкая мебель, и корпусная мебель. Вся мебель, построенная по принципу танграма, довольно удобна и функциональна. Она может видоизменятся в зависимости от настроения и желания хозяина. Сколько всевозможных вариантов и комбинаций можно составить из треугольных, квадратных и четырехугольных полок. При покупке такой мебели вместе с инструкцией покупателю выдаются несколько листов с картинками на разные темы, которые можно сложить из этих полок. В гостиной можно повесить полки в виде людей, в детской из этих же полок можно сложить котов, зайцев и птиц, а в столовой или библиотеке — рисунок может быть на строительную тему — дома, замки, храмы.
Вот такой многофункциональный танграм.
1.Оргмомент
| Начнем урок словами французского писателя А.Франса: “Учиться можно весело… Чтобы переварить знания, надо поглощать их с аппетитом”. Последуем этому совету, постараемся быть внимательными, будем поглощать знания с большим желанием, т.к. они пригодятся нам в дальнейшем. | Рапорт дежурного | 2. Словарная работа Проверка домашнего задания | Запишем тему урока: «Классификация параллелограммов. Прямоугольник, ромб, квадрат». Обратите внимание на то, как пишется слово параллелограмм. | Ответы: Проверка домашнего задания. Работа в парах (взаимоконтроль). | 3.Объяснение нового материала | Сегодня на уроке мы будем изучать частные виды параллелограмма. Это – прямоугольник, ромб, квадрат. Перед вами первый вид параллелограмма – прямоугольник. Давайте дадим ему определение. Закончите предложение: прямоугольник – параллелограмм, у которого… А как еще можно определить прямоугольник? Сколько достаточно иметь прямых углов параллелограмму, чтобы он стал прямоугольником? А можно ли дать определение прямоугольника через четырехугольник? Если да, то продолжите предложение: прямоугольник – четырехугольник, у которого… Итак, прямоугольник – это параллелограмм, значит какими уже известными вам свойствами, он обладает? А что вы можете сказать о диагоналях прямоугольника? Ребята, а теперь подумайте и ответьте на вопрос. Устно доказывается признак прямоугольника. Учащиеся делают чертеж и необходимые краткие записи определения, свойства и признака прямоугольника в тетрадях. Индивидуальная работа с обучающимися по сниженной программе. Перед вами второй вид параллелограмма – ромб. Давайте дадим ему определение. Закончите предложение: ромб – параллелограмм, у которого… А как еще можно определить ромб? Равенство каких сторон параллелограмма достаточно, чтобы он стал ромбом? А можно ли дать определение ромба через четырехугольник? Если да, то продолжите предложение: ромб – четырехугольник, у которого… А теперь давайте сформулируем свойства ромба, кроме тех, которые он уже имеет, являясь параллелограммом. Новые свойства касаются диагоналей ромба. Что вы скажите про треугольник АВD? Чем является в этом треугольнике отрезок АО? Каковы же свойства диагоналей ромба? Ребята, а как вы считаете, доказанные выше свойства могут быть и признаками ромба? Закончите предложение: параллелограмм – ромб, если… Устно доказываются признаки ромба. Учащиеся делают чертеж и необходимые краткие записи определения, свойств и признаков ромба в тетрадях. Индивидуальная работа с Индивидуальная работа с обучающимися по сниженной программе. (Оценить ответы) | Ответы учащихся все углы прямые. один прямой угол. все углы прямые. Ответ: 1) противоположные стороны равны; 2) противоположные углы равны; 3) диагонали точкой пересечения делятся пополам. диагонали у прямоугольника равны. диагонали равны. На карточке самостоятельно начертить прямоугольник все стороны равны. равенство смежных сторон. все стороны равны. Ответы учащихся диагонали ромба перпендикулярны На карточке самостоятельно начертить квадрат | И наконец, самым идеальным видом параллелограмма является квадрат. Ребята, а как вы думаете, почему я назвала квадрат идеальным видом параллелограмма? (Оценить ответ) Самостоятельно в тетрадь обучающимися по сниженной программе Начертить произвольный четырехугольник. | Самоконтроль Ответы: 1) все углы прямые; 2) все стороны равны. квадрат обладает свойствами и параллелограмма, и ромба и прямоугольника. | 4.Закрепление новых знаний | Итак, давайте еще раз повторим все, что мы знаем о квадрате. Ребята, для того, чтобы привести в систему все ваши знания о параллелограммах и их свойствах, посмотрите внимательно на следующую схему. Давайте повторим определения параллелограмма и его видов. (Вести соответствующее комментирование появляющейся на экране первой части схемы, привлекая к этому и самих учащихся). (Оценить ответ) Перед вами все свойства параллелограммов 1–6. Давайте вспомним, какие свойства (они объединены по группам) к какой фигуре относятся. (Вести соответствующее комментирование появляющейся на экране второй части схемы, привлекая к этому и самих учащихся). Задание 2. (работа в парах) Опираясь на схему, рассказать друг другу свойства параллелограмма и его видов. Задание 3. (Распечатать слайд 11 и раздать лист со схемой каждому ученику) Заполнить в данной схеме пропуски, вместо которых записать, используя математические обозначения, определения или свойства параллелограммов. Задание 4. Решить задачи по готовым чертежам Если класс хорошо усвоил материал, то задачи можно решить устно. Задание 5. Проверочная работа. Индивидуальная работа с обучающимися по сниженной программе (Оценить ответы) | (работа в парах) Опираясь на схему, рассказать друг другу определения параллелограмма и его видов. Ученики проверяют правильность заполнения пропусков в схеме на раздаточном листе и оставляют этот лист у себя, чтобы пользоваться этой схемой на уроках. |
Глава V. Об определении – Учебник логики, Г. Челпанов
Цель определения. Когда мы произносим какое-либо слово, соответствующее известному понятию, и хотим сделать его понятным для всех, то мы должны раскрыть содержание понятия, соответствующего указанному слову, а так как содержанием понятия называется совокупность его признаков, то раскрытие содержания понятия можно обозначить как перечисление признаков, присущих данному понятию. Какое-либо понятие A содержит признаки a, b, c, d; если мы перечислим эти признаки, то тем самым точно обозначим, раскроем содержание понятия A; это значит, другими словами, что мы определим его.
Следует заметить, что не все понятия могут быть определены. Понятия по своему содержанию бывают весьма различны: содержание одних понятий больше, других – меньше.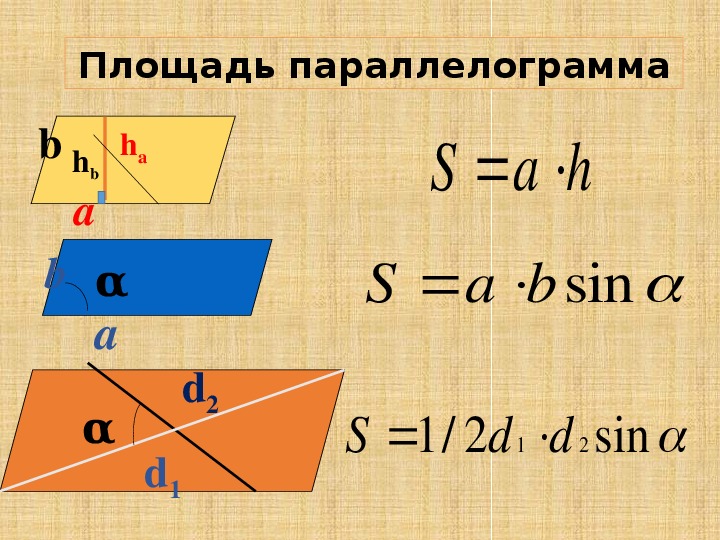 Такие понятия, которые имеют сложное содержание, т.е. такие, которые имеют много признаков, могут быть определены. Но есть понятия, которые имеют настолько простое содержание, что не могут быть определены, потому что, как было сказано, для определения необходимо раскрытие содержания понятия; если же содержание понятия не может быть раскрыто, то оно не может быть и определено. Такие понятия называются простыми. Например, понятие «пунцовый цвет» не подлежит определению: цвет этот нужно видеть, чтобы знать, что он такое. Всё же определения, которые мы попытались бы дать в данном случае, были бы ложными в логическом отношении. Точно так же определять, что такое тон известной высоты, бесполезно; это усваивается, понимается непосредственным восприятием этого тона. Сюда же относятся такие понятия, как, например, понятия «равенство», «тождество», «тяжесть», «протяжение», «сознание» и т.п. Точно так же не могут быть определяемы индивидуальные понятия, потому что при определении их пришлось бы перечислить бесконечное множество признаков.
Такие понятия, которые имеют сложное содержание, т.е. такие, которые имеют много признаков, могут быть определены. Но есть понятия, которые имеют настолько простое содержание, что не могут быть определены, потому что, как было сказано, для определения необходимо раскрытие содержания понятия; если же содержание понятия не может быть раскрыто, то оно не может быть и определено. Такие понятия называются простыми. Например, понятие «пунцовый цвет» не подлежит определению: цвет этот нужно видеть, чтобы знать, что он такое. Всё же определения, которые мы попытались бы дать в данном случае, были бы ложными в логическом отношении. Точно так же определять, что такое тон известной высоты, бесполезно; это усваивается, понимается непосредственным восприятием этого тона. Сюда же относятся такие понятия, как, например, понятия «равенство», «тождество», «тяжесть», «протяжение», «сознание» и т.п. Точно так же не могут быть определяемы индивидуальные понятия, потому что при определении их пришлось бы перечислить бесконечное множество признаков. Например: «этот бриллиант».
Итак, определить то или иное понятие значит перечислить его признаки. Но это представляется иногда задачей трудной, потому что количество признаков того или другого понятия может быть очень велико; поэтому перечислить даже большинство этих признаков не окажется возможным. Если бы, например, определяя понятие «прямоугольник», мы сказали, что прямоугольник есть геометрическая фигура, плоская, ограниченная прямыми линиями, четырёхугольная, с прямыми углами и т.д., то это определение было бы правильно, но практически оно неудобно, потому что перечисляется целый ряд признаков. Вследствие этого принят другой способ определения понятий, который имеет целью избежать полного перечисления признаков. Он заключается в следующем.
Дадим определение прямоугольника. Для этой цели мы воспользуемся понятием «параллелограмм». Когда мы употребляем термин «параллелограмм», то под ним мы понимаем или прямоугольник, или ромб, или квадрат. Зная это, мы не будем говорить «прямоугольник есть геометрическая фигура, плоская, ограниченная прямыми линиями, четырёхугольная» и т.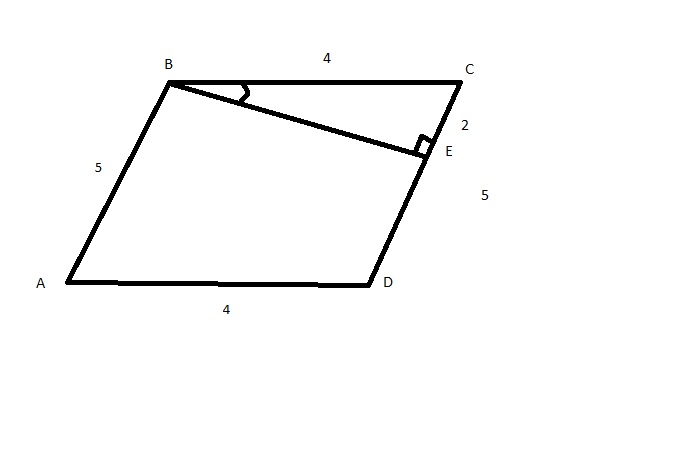 д., а просто скажем, что это есть «параллелограмм, в котором все углы прямые», ибо всякий под словом «параллелограмм» разумеет геометрическую фигуру, ограниченную четырьмя прямыми, попарно параллельными линиями; прибавляя, что все углы фигуры прямые, мы окончательно завершаем определение её именно тем, что мы отличаем прямоугольник от ромба и от квадрата, которые тоже суть параллелограммы. Таким образом, определяя понятие «прямоугольник», мы указали род данного понятия (параллелограмм) и присоединили к нему видовое различие его (четыре прямых угла), отличающее его от других видов, входящих в тот же род, т.е. от ромба и квадрата. Руководствуясь тем же правилом, мы скажем, что «ромб есть параллелограмм, в котором все стороны равны», а «квадрат есть параллелограмм, в котором стороны и углы равны».
д., а просто скажем, что это есть «параллелограмм, в котором все углы прямые», ибо всякий под словом «параллелограмм» разумеет геометрическую фигуру, ограниченную четырьмя прямыми, попарно параллельными линиями; прибавляя, что все углы фигуры прямые, мы окончательно завершаем определение её именно тем, что мы отличаем прямоугольник от ромба и от квадрата, которые тоже суть параллелограммы. Таким образом, определяя понятие «прямоугольник», мы указали род данного понятия (параллелограмм) и присоединили к нему видовое различие его (четыре прямых угла), отличающее его от других видов, входящих в тот же род, т.е. от ромба и квадрата. Руководствуясь тем же правилом, мы скажем, что «ромб есть параллелограмм, в котором все стороны равны», а «квадрат есть параллелограмм, в котором стороны и углы равны».
Итак, определение заключается в указании рода данного понятия с присоединением видового различия его. Это в логике принято обозначать при помощи формулы: «Definitio fit per genus et differentiam specificam», т.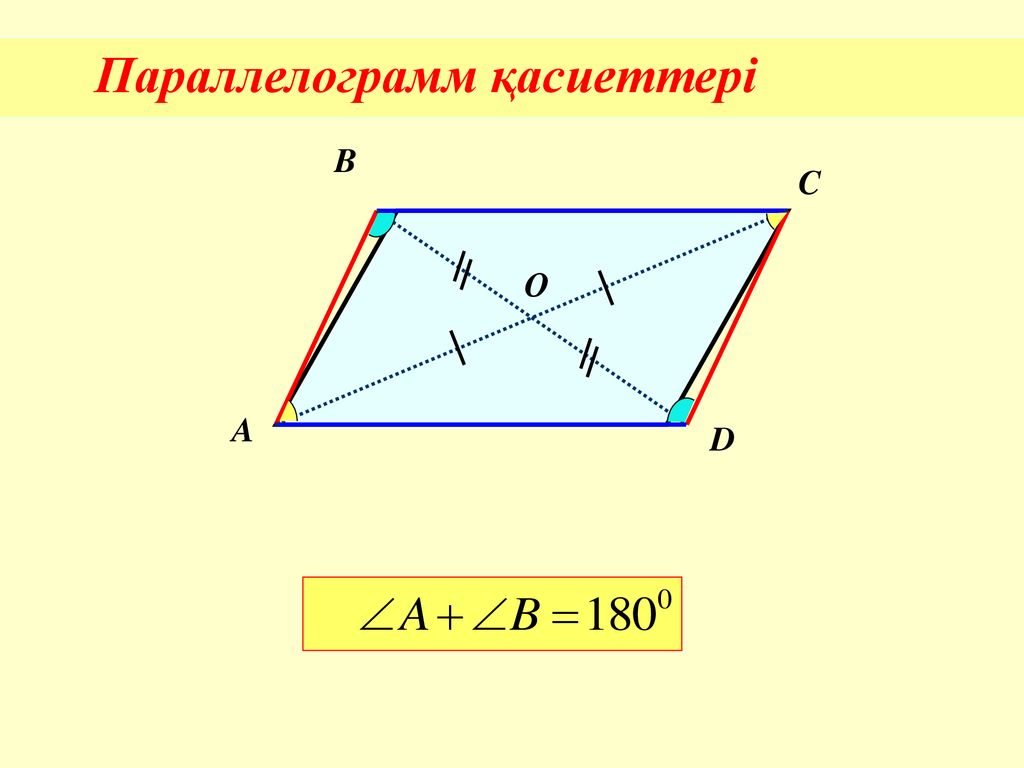 е. определение совершается при помощи рода и видового различия.
е. определение совершается при помощи рода и видового различия.
Если нам нужно определить какое-либо понятие, то мы выражаем наше определение при помощи суждения, содержащего подлежащее и сказуемое. Подлежащее этого суждения называется определяемым (definiendum), сказуемое называется определяющим (definiens). Эти термины важны потому, что благодаря им мы можем указать те правила, при соблюдении которых получается правильное определение. Таких правил четыре.
Другие в этой формуле прибавляют к genus термин proximum: «definitro fit per genus proximum et differentiam specificam» («определение совершается при помощи ближайшего рода и видового различия»), желая этим указать на то, что следует пользоваться ближайшим родовым понятием.
1. Определение должно быть соразмерным, т.е. таким, в котором объёмы определяемого и определяющего тождественны, т.е. одинаково велики. Если правило это нарушено, то определение неадекватно, или несоразмерно. В таком случае определение делается или слишком широким или слишком узким, именно, если объём определяющего становится слишком широким или слишком узким в сравнении с объёмом определяемого. Возьмём в пример определение лошади. Если сказать, что «лошадь есть домашнее животное», то это определение будет слишком широким; в нём объём определяющего будет более широким, чем объём определяемого понятия (в объём домашнего животного, кроме лошади, входят ещё коровы, собаки и т.п.). Относительно такого определения можно также сказать, что в него не входит указание существенного признака данного понятия. Если в определении опущены существенные признаки понятия, тогда оно окажется слишком широким, как в только что приведённом примере.
Возьмём в пример определение лошади. Если сказать, что «лошадь есть домашнее животное», то это определение будет слишком широким; в нём объём определяющего будет более широким, чем объём определяемого понятия (в объём домашнего животного, кроме лошади, входят ещё коровы, собаки и т.п.). Относительно такого определения можно также сказать, что в него не входит указание существенного признака данного понятия. Если в определении опущены существенные признаки понятия, тогда оно окажется слишком широким, как в только что приведённом примере.
Возьмём определение, которое погрешает в противоположном направлении. Если бы мы сказали, что «треугольник есть плоская прямолинейная фигура, имеющая три равные стороны», то это определение было бы слишком узким. В нём объём определяющего понятия меньше объёма определяемого понятия. Именно: в объём определяющего понятия входят только равносторонние треугольники, а в объём определяемого понятия входят как равносторонние, так и неравносторонние треугольники.
2. Определение не должно делать круга. Это правило требует, чтобы определяемое понятие не определялось посредством понятия, которое само делается понятным только посредством определяемого. Возьмём, например, определение «вращение есть движение вокруг оси». Это определение понятия «вращение» посредством понятия «ось» делает круг, ибо само понятие «ось» определяется только через понятие «вращение» (как известно, ось – это прямая, вокруг которой происходит вращение). Таким образом, ясно, что в нашем определении получается круг: понятие «вращение» определяется посредством понятия «ось», а понятие «ось» – посредством понятия «вращение».
В определении определяющее и определяемое должны быть двумя различны ми и притом самостоятельными понятиями. Если это не соблюдается, то получается ошибка, которая называется idem per idem, или тавтологией, именно: в определении получается только повторение того же слова, т.е. употребляются слова, имеющие то же самое значение. Например: «свет есть то, чему присущ свет»; «величина есть то, что способно уменьшаться и увеличиваться».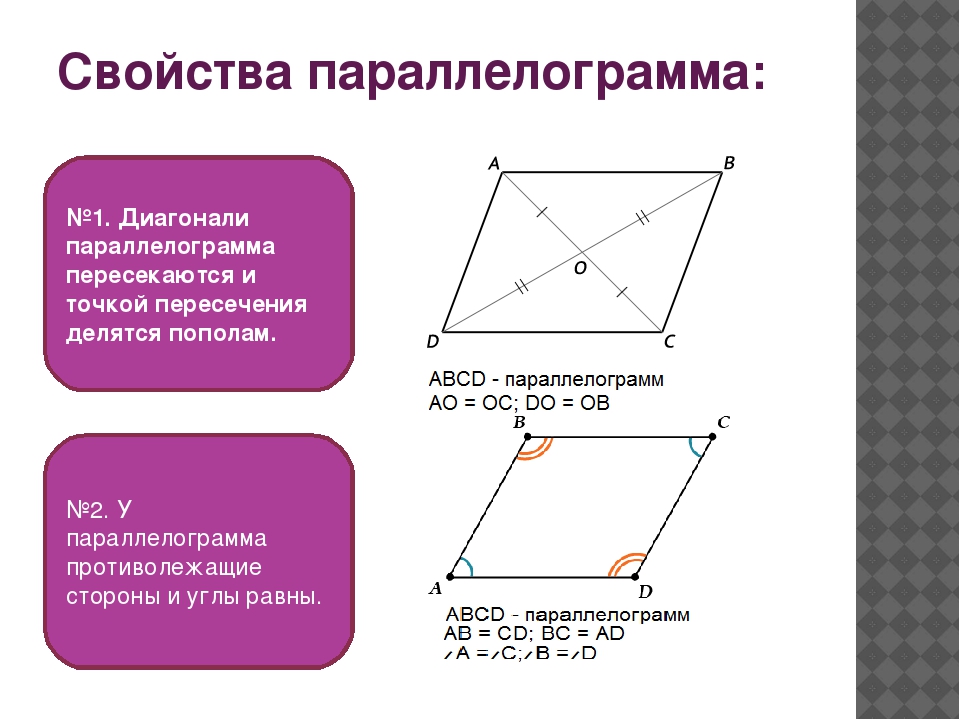 Последнее определение представляет собой тавтологию, потому что уменьшение есть убавление величины, увеличение же есть прибавление величины, а потому, если мы определяем величину посредством того, что способно увеличиваться или уменьшаться, то очевидно, что в определяющем понятии содержится определяемое понятие.
Последнее определение представляет собой тавтологию, потому что уменьшение есть убавление величины, увеличение же есть прибавление величины, а потому, если мы определяем величину посредством того, что способно увеличиваться или уменьшаться, то очевидно, что в определяющем понятии содержится определяемое понятие.
3. Определение не должно быть отрицательным, оно должно указывать признаки, присущие данному понятию, а не чуждые ему, ибо эти последние для нас неважны и, кроме того, их можно указать очень много. Например, возьмём определение «театр есть здание, не служащее для жилья». Если A будет здание, служащее для жилья, то не-A, или зданий, не служащих для жилья, будет бесчисленное множество. Таким образом, это определение делается для нас непригодным. К числу определений, которые вследствие своего отрицательного характера непригодны, нужно отнести следующие: «жидкость есть то, что не твёрдо и не газообразно», «точка есть то, что не имеет частей и не имеет никакой величины». Отрицательные определения не раскрывают содержания понятия, они оставляют содержание понятия неопределённым. Поэтому отрицательные определения не отвечают главной цели определения – раскрыть содержание определяемого понятия, сделать содержание понятия определённым.
Отрицательные определения не раскрывают содержания понятия, они оставляют содержание понятия неопределённым. Поэтому отрицательные определения не отвечают главной цели определения – раскрыть содержание определяемого понятия, сделать содержание понятия определённым.
Отрицательные определения могут быть употребляемы только тогда, когда определяемое понятие имеет отрицательный характер. Например, «чужестранец» – это человек, не принадлежащий к данной стране, и т. д.
4. Определение должно быть ясным, т.е. в определении нельзя пользоваться выражениями двусмысленными, метафорическими и вообще мало понятными. Нарушение этого правила приводит к попытке сделать понятным неизвестное через посредство ещё менее известного (ignotum per ignotius). Например, выражения «архитектура есть застывшая музыка» и «нужда есть мать изобретения» – это есть образные выражения, которые не объясняют значения термина. Если же сказать, что «эксцентричность есть своеобразная идиосинкразия», то мы непонятное пытаемся объяснить посредством непонятного же.
Приёмы, заменяющие определения. Итак, чтобы наши определения были точны, они должны удовлетворять указанным четырём сословиям. Но не следует думать, что все наши понятия могут быть всегда определяемы указанным способом. Есть случаи, когда нам приходится знакомиться с содержанием понятия не посредством определения, а иными способами. Можно указать следующие способы, заменяющие определение.
1. Указание. Если, например, мы кого-нибудь желаем познакомить с тем, что такое тот или другой цвет, звук и т.п., то это мы будем в состоянии сделать только в том случае, если приведём его в соприкосновение с данным цветом, звуком и т.п., т.е. вставим его воспринимать то, с чем мы желаем его ознакомить. Такой способ ознакомления с известным понятием называется указанием. Указание употребляется во всех случаях, когда нам приходится знакомить кого-нибудь с предметами непосредственного восприятия:
2. Описание употребляется при ознакомлении с индивидуальными предметами или при ознакомлении со свойствами, принадлежащими какой-либо вещи. В таком случае приводятся возможно точно и полно признаки этой вещи, например описание Днепра у Гоголя, Рейнского водопада у Карамзина и т.п. В ботанике описывается строение того или иного цветка, процесс опыления и т.п., в химии описывается та или иная реакция.
В таком случае приводятся возможно точно и полно признаки этой вещи, например описание Днепра у Гоголя, Рейнского водопада у Карамзина и т.п. В ботанике описывается строение того или иного цветка, процесс опыления и т.п., в химии описывается та или иная реакция.
3. Характеристика приводит выдающиеся признаки какого-либо предмета или явления. Если нам нужно познакомить кого-нибудь с тем, что такое «воображение построительное» и «воображение воспроизводящее», то мы вместо определения можем указать на какую-нибудь существенную черту, присущую тому или другому виду воображения, например, говорим, что для построительного воображения существенным является новизна сочетания, а для воспроизводящего – точность. Какое-нибудь свойство является характерным для того или другого лица: для воина – мужество, для врача – гуманность и т.п. Характерной особенностью семейства крестоцветных растений являются цветы с четырьмя листочками чашечки и четырьмя лепестками венчика, расположенными крест-накрест, с двумя короткими и четырьмя длинными тычинками.
4. Сравнение употребляется в том случае, когда мы знакомимся с тем или иным понятием при помощи сравнения его с другими понятиями, похожими на него. Мы можем дать понятие о теплопроводности какого-либо тела при помощи сравнения её со светопрозрачностью, например, если скажем, что теплопроводность по отношению к тепловым лучам есть то же самое, что прозрачность по отношению к световым лучам. Сравнение употребляется главным образом тогда, когда одно понятие уясняется при помощи другого понятия, более ясного, например, когда какое-либо абстрактное понятие уясняется при помощи какого-либо конкретного. Например, «жизнь есть школа опыта», «право есть воплощение, нравственной идеи», «совесть есть внутренний суд».
5. Различение употребляется в том случае, когда мы знакомим кого-нибудь с содержанием какого-либо понятия, указывая на то различие, которое существует между данным понятием и другими, например, если мы говорим, что «энтузиазм» отличается от «фанатизма» тем, что он вызывается чем-либо благородным и не переходит за пределы умеренности.
Вопросы для повторения
Что такое содержание понятия? Что такое сложные и простые понятия? Какие понятия не могут быть определены? Что такое определение? Перечислите условия правильности определения. Какие определения будут слишком узкие и какие слишком широкие? Когда определение делает круг? Почему признаки, входящие в определение, не должны иметь отрицательного характера? Назовите приёмы, заменяющие определение, и укажите особенности каждого приёма.
Вариативные тестовые вопросы по геометрии (Варианты 1-4 по 12 вопросов с отметками правильных ответов)
Тест 5. Тема: Параллелограмм, прямоугольник, ромб, квадрат
Цель данного теста — проверить, умеет ли учащийся:
¾ при анализе геометрических конфигураций пользоваться определением и свойствами параллелограмма, ромба, прямоугольника, квадрата для нахождения их элементов.
Вариант 1
Записывая ответы
на задания теста, обведите буквы, отвечающие утверждениям,
которые вы считаете правильными, и зачеркните буквы, отвечающие утверждениям,
которые вы считаете неправильными. Например, если вы считаете правильными утверждения А и В, а неправильными — утверждения
Б и Г, запишите . Если хотя бы одна буква из 4-х будет не отмечена, задание считается невыполненным.
Например, если вы считаете правильными утверждения А и В, а неправильными — утверждения
Б и Г, запишите . Если хотя бы одна буква из 4-х будет не отмечена, задание считается невыполненным.
|
1. Дан параллелограмм ABCD, в котором AB = 5 см, AD = 7 см, A = 30°. Выберите правильное утверждение. –А. DC = 7 см. +Б. BC = 7 см. –В. ÐC = 150°. –Г. D > B. |
|
2. Дан прямоугольник ABCD, у которого диагональ АС = 10 см, точка O — точка пересечения диагоналей. Выберите правильное утверждение. –А. OB = 6 см. –Б. AO
> BO. –В. BAD > ABC. +Г. BD = 10 см. |
|
3. Дан ромб ABCD, у которого АВ = 7 см. Выберите правильное утверждение. –А. Треугольник ABC неравнобедренный. +Б. Периметр ромба равняется 28 см. –В. AD может равняться 6 см. –Г. ВС > CD. |
|
4. Дан параллелограмм ABCD, у которого a = 35°, g = 45° (см. рисунок). Отметьте, какие из следующих четырех утверждений правильные, а какие — неправильные. –А. ÐB > ÐD. –Б. AB
+ BC > AD + DC. +В. d = . +Г. ÐBAD = 80°. |
|
5. Диагонали прямоугольника ABCD пересекаются в точке О. Известно, что AD = 9 м, AO = 6 м. Отметьте, какие из следующих четырех утверждений правильные, а какие — неправильные. +А. AC = 2AO. –Б. BD < 11 м. –В. BC = 6 м. +Г. Периметр треугольника BOC больше 18 м. |
|
6. Четырехугольник ABCD — ромб, в
котором O — точка пересечения диагоналей, OD = 6 м,
OC =
= 8 м. Отметьте, какие из следующих четырех
утверждений правильные, а какие — неправильные. –А. AC < 15 м. +Б. ÐBAC = ÐCAD. –В. BC + AD может быть больше AB + CD. +Г. АО — высота треугольника ABD. |
7. Дан параллелограмм ABCD. На сторонах ВС и AD взяты соответственно точки Е и F так, что BE = DF, О — точка пересечения BD и EF. Отметьте, какие из следующих четырех утверждений правильные, а какие — неправильные.
–А. BEFА — параллелограмм.
–Б. BO > OD.
+В. Прямая AC проходит через точку О.
–Г. BE + AF < AD.
8. Дан прямоугольный треугольник АВС.
Через точку М, принадлежащую гипотенузе, проведены прямые, параллельные
катетам и пересекающие катет AC в точке K и катет ВС в
точке L. Отметьте, какие из следующих четырех утверждений правильные, а
какие — неправильные.
Отметьте, какие из следующих четырех утверждений правильные, а
какие — неправильные.
+А. CKML —прямоугольник.
–Б. KL > MC.
+В. Если KM = ML, то отрезок KL перпендикулярен MC.
–Г. KM + LB < CB.
9. Дан квадрат ABCD. На диагонали AC взяты точки М и N так, что AM = CN, причем AM < 0,5 AC. Отметьте, какие из следующих четырех утверждений правильные, а какие — неправильные.
–А. Треугольники АМВ и CND могут быть не равными.
–Б. Четырехугольник BMDN — обязательно является квадратом.
–В. ÐBNC < ÐDNC.
–Г. ÐDBN + ÐBDM = 90°.
10. На сторонах параллелограмма ABCD
взяты точки K, L, M, N так, что AK : KB = CL : LB = CM : MD = AN : ND,
О — точка пересечения AC и KM. Отметьте, какие
из следующих четырех утверждений правильные, а какие — неправильные.
Отметьте, какие
из следующих четырех утверждений правильные, а какие — неправильные.
+А. Середины отрезков LN и KM обязательно совпадают.
+Б. Прямые KM, LN и BD обязательно пересекаются в точке O.
–В. KO обязательно равно LO.
+Г. Если KМ — биссектриса угла LKN, то LN — биссектриса угла KLM.
11. Дан прямоугольник ABCD, не являющийся квадратом. Биссектриса угла А пересекает биссектрисы углов B и D соответственно в точках K и L, биссектриса угла С пересекает биссектрисы углов B и D соответственно в точках N и M. Отметьте, какие из следующих четырех утверждений правильные, а какие — неправильные.
–А. Угол между биссектрисами углов А и В может быть острым.
+Б. KLMN — прямоугольник.
+В. Отрезок
KM обязательно перпендикулярен LN.
+Г. KМ обязательно равно LN.
12. Дан параллелограмм ABCD, у которого угол A острый. Из вершины угла B на стороны AD и CD опущены перпендикуляры, основаниями которых являются соответственно точки K и L. Отметьте, какие из следующих четырех утверждений правильные, а какие — неправильные.
+А. BK может равняться BL.
+Б. Если треугольники BKA и BLC равны, то ABCD — ромб.
–В. ÐKBL = 2A.
–Г. ÐBKL всегда равно .
Вариант 2
Записывая ответы
на задания теста, обведите буквы, отвечающие утверждениям,
которые вы считаете правильными, и зачеркните буквы, отвечающие утверждениям,
которые вы считаете неправильными.
Например, если вы считаете правильными утверждения А и В, а неправильными — утверждения
Б и Г, запишите . Если хотя бы одна буква из 4-х будет не отмечена, задание считается невыполненным.
|
1. Дан параллелограмм ABCD, в котором О — точка пересечения диагоналей, АО = 6 мм. Выберите правильное утверждение. –А. BО > OD. –Б. BO < OD. –В. АВ ¹ DC. +Г. AC = 12 мм. |
|
2. Дан прямоугольник ABCD, в котором О — точка пересечения диагоналей, a = 25°. Выберите правильное утверждение. –А. AC ¹ BD. +Б. b = 65°. –В. a + g = 60°. –Г. OB < OA. |
|
3. +А. b = 35°. –Б. KN¹ NM. –В. KL < NM. –Г. ¹ . |
|
4. Сумма длин всех сторон параллелограмма ABCD равна 24 м, а сумма длин |
Распечатать форму параллелограмма — Распечатать бесплатную форму параллелограмма
Перейти к основному содержанию- ФОРМЫ
- ЛАБИРИНТЫ
- НОМЕР ОБРАБОТКИ ЛИСТОВ
- ЛИСТЫ ОТСЛЕЖИВАНИЯ БУКВ
- ДОМ
- СКРАМБЛЫ СЛОВАМИ
- ПИСЬМА
- НОМЕРА
- ЖИВОТНЫЕ
- ЗАГАДКИ ПОИСКА СЛОВ
| Просмотреть все формы |
Версия для печати
`
Пропустить боковые навигационные ссылки
Печатные формы
- Дом
- Печатные схватки со словами
- Печатные буквы
- Числа для печати
- Животные для печати
- Пазлы для поиска слов
- Печатные этикетки для консервных банок
- Формы для печати
- Лабиринты для печати
- Раскраски с буквами для печати
- Листы для отслеживания номеров для печати
- Печатаемые листы для отслеживания писем
- Печатные таблицы преобразований
- Распечатанная таблица целей экономии денег
- Игра в крестики-нолики для печати
- Игра в точки для печати
- Игра для печати в палача
- Рождественские раскраски для печати
- Рождественский список желаний для печати
- Рождественские силуэты для печати
- Часы для печати
- Глазная диаграмма для печати
- Карты состояний для печати
- Карты континентов для печати
- Периодическая таблица для печати
- Знаки зодиака для печати
- Буквы для печати на классной доске
- Силуэтные буквы для печати
- Трафареты для печати букв
- Буквы для печати курсивом
- Цифры для печати на классной доске
- Для печати силуэтных чисел
- Трафареты для печатных номеров
- Печатный счетчик по числовым диаграммам
- Печатная таблица умножения
- Дни недели для печати
- Месяцы года для печати
- Список мировых континентов для печати
- Вывеска для печати 1-го дня детского сада
© PrintableParadise.
 ком
комPython Math: вычислить площадь параллелограмма
Python Math: Упражнение 4 с решением
Напишите программу на Python для вычисления площади параллелограмма.
Примечание: Параллелограмм — это четырехугольник, противоположные стороны которого параллельны (и, следовательно, противоположные углы равны). Четырехугольник с равными сторонами называется ромбом, а параллелограмм, все углы которого равны прямым, называется прямоугольником.
Пример раствора : —
Код Python:
base = float (input ('Длина основания:'))
height = float (input ('Измерение высоты:'))
площадь = основание * высота
print ("Площадь:", площадь)
Пример вывода:
Длина основания: 5 Измерение роста: 6 Площадь: 30.0
Изображение:
Схема:
Визуализировать выполнение кода Python:
Следующий инструмент визуализирует, что делает компьютер, шаг за шагом, когда он выполняет указанную программу:
Редактор кода Python:
Есть другой способ решить эту проблему? Разместите свой код (и комментарии) через Disqus.
Предыдущая: Напишите программу на Python для вычисления площади трапеции.
Далее: Напишите программу на Python для вычисления объема поверхности и площади цилиндра.
Python: советы дня
Упростите способ сворачивания вложенных списков:
х = [
[1, 2, 3],
[4, 5, 6],
[7, 8, 9]
]
Икс
Выход:
[[1, 2, 3], [4, 5, 6], [7, 8, 9]]
результат = []
для подсписка в x:
для элемента в подсписке:
result.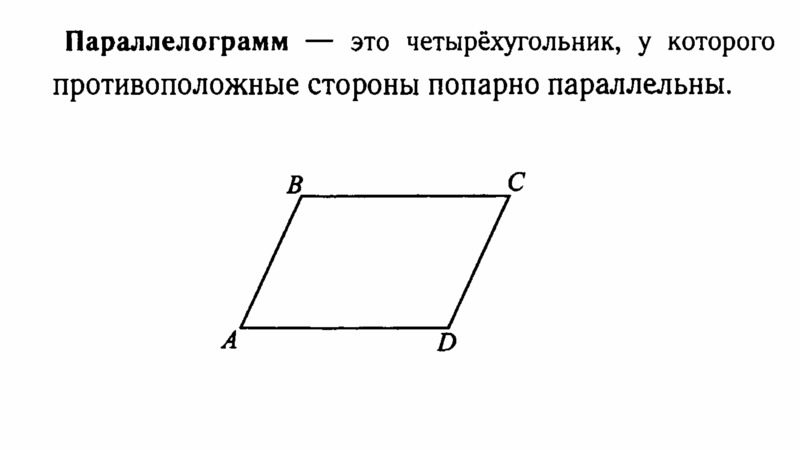 append (элемент)
результат
append (элемент)
результат
Выход:
[1, 2, 3, 4, 5, 6, 7, 8, 9]
[элемент для подсписка в x для элемента в подсписке]
Выход:
[1, 2, 3, 4, 5, 6, 7, 8, 9]
импорт itertools itertools.цепь (* x)
Выход:
список (itertools.chain (* x))
Выход:
[1, 2, 3, 4, 5, 6, 7, 8, 9]
параллелограммов 101 и Дженни, блок № 45 в жене фермера 1930-е гг., Прошитые по
Параллелограмм: любая 4-сторонняя форма с 2 парами противоположных параллельных сторон равной длины. Противоположные углы также совпадают.Параллелограмм — это не квадрат, а квадрат — это параллелограмм.Кроме того, ромбы представляют собой параллелограммы с 4 равными сторонами.
Прямо здесь, вы можете бормотать, что, если бы вы знали, что собираетесь делать лоскутное одеяло, вы бы обратили внимание на уроке геометрии! Я хотел бы помочь вам освоиться с параллелограммами и другими элементами геометрии квилта.
Один часто используемый параллелограмм квилтера создается путем соединения двух прямоугольных треугольников под 45 градусов, или того, что квилтеры обычно называют полуквадратными треугольниками (HST). В зависимости от конструкции блока они могут соединяться прямым волокном на ножках или гипотенузе.
Дженни нужна прямая линия гипотенузы. Следуя диаграмме преобразования, чтобы создать блок Дженни, вы научитесь вырезать параллелограмм с помощью шаблона треугольника и устранить шов. Вы можете спросить: «Если вы можете просто сшить два треугольника вместе, чтобы получился параллелограмм, зачем вам нужно вырезать цельный параллелограмм?»
Потому что вы хотите…
- устранить лишние швы, что уменьшает объем и объем работы.
- защищает целостность тканевых конструкций.Никто не хочет шов посередине полосы или другого направленного принта, самых крупных принтов или суетливых рисунков.
- улучшите свои навыки лоскутного шитья!
 Однако, прежде чем вы закончите это квилт, вы будете хорошо знакомы с параллелограммами! Параллелограммы направленные. Интересно, что в этом блоке все они указывают в одну сторону, в верхний правый угол. Если вы не работаете с батиком, твердыми телами или красками для рук, после того, как вы вырежете параллелограмм, его нельзя повернуть в другую сторону, поэтому все параллелограммы Дженни вырезаются тканью лицевой стороной вверх.
Однако, прежде чем вы закончите это квилт, вы будете хорошо знакомы с параллелограммами! Параллелограммы направленные. Интересно, что в этом блоке все они указывают в одну сторону, в верхний правый угол. Если вы не работаете с батиком, твердыми телами или красками для рук, после того, как вы вырежете параллелограмм, его нельзя повернуть в другую сторону, поэтому все параллелограммы Дженни вырезаются тканью лицевой стороной вверх.Что, если?
Что делать, если вы забыли разрезать ткань лицевой стороной вверх?- Если обе полоски лежат правой стороной вниз, рисунок просто будет вращаться в другом направлении. Хорошо!
- Если полосы были соединены правильной или неправильной стороной, вы получите зеркальное отображение параллелограммов, и вам нужно будет разрезать снова. В блоках квилта довольно часто пары параллелограммов являются блоками зеркального отображения, но в этом блоке это не так. Однако когда мы приступим к созданию блоков с зеркальными параллелограммами, вы уже будете знать, как это делать! 🙂
Представляем трюк с обрезкой наполовину / наполовину
В нашей таблице преобразования Дженни показано размещение шаблона наполовину на конце полосы, наполовину от края полосы, чтобы начать резку первого параллелограмма для правосторонней резки. Если вы левша, начните с правого конца полосы и расположите треугольный шаблон таким же образом, наполовину вкл., Наполовину выкл. Такой путь эффективен; значит вырезать каждый треугольник из полосы будет легко и удобно.
Если вы левша, начните с правого конца полосы и расположите треугольный шаблон таким же образом, наполовину вкл., Наполовину выкл. Такой путь эффективен; значит вырезать каждый треугольник из полосы будет легко и удобно. Наши методы резки нацелены на то, чтобы ваша режущая рука и роторный резак были правильно расположены по отношению к акриловым инструментам. То есть, как правило, вы будете резать более точно, если ваша рука и дисковый резак находятся справа от акрилового инструмента, если вы правша, и слева от акрилового инструмента, если вы левша.
От Marti Michell шаблоны могут выполнять множество трюков с вырезанием, в том числе вырезать форму, для которой нет шаблона, например параллелограмм, и обрезать ее до нужного вам размера. Некоторые из наших методов поначалу могут показаться неудобными, потому что вы к ним не привыкли, но по мере того, как мы будем шить, я думаю, вы поймете преимущества вырезания определенных форм с помощью трюка с вырезанием.

Знакомьтесь, Дженни!
Спереди и сзади. Нажмите на фото, чтобы увидеть увеличенное изображение.Щелкните ссылку, чтобы загрузить диаграмму преобразования шаблона для этого блока:
для блока № 45, Дженни
В дополнение к нашей загрузке PDF-файла для преобразования шаблонов, вы захотите прочитать руководства Gnome Angel для этих блоков.
В Образец лоскутного одеяла 1930-х годов жены фермера: вдохновляющие письма фермерских женщин Великая депрессия и 99 блоков лоскутного одеяла в их честь Лори Аарон Хирд для Fons & Porter / F + W.
трехлепестковых записей: TLR 109-113: параллелограмм
TLR 109-113: параллелограмм Сборник из 5 пластинок + скачать
выпущен * в конце * декабря 2015 г.примерно 950 сборники (5 пластинок) доступны из трех пластинчатых записей на 140 г черном виниловые и помещенные в спичечные коробки с высокой печатью. из печати.
доступно для заказа как прямая цифровая загрузка с bandcamp по этим ссылкам: TLR-109 (шипит золотой вестник / майкл чепмен), TLR-110 (шесть органов допуска / уильям тайлер), TLR-111 (Курт Вайл / Стив Ганн), TLR-112 (Терстон Мур и Джон Молони: записано на пленку / епископ — orcutt — Корсано) и TLR-113 (пруд бардо / йо ла тенго)
есть особая магия
это происходит от нахождения правильного музыкального сочетания.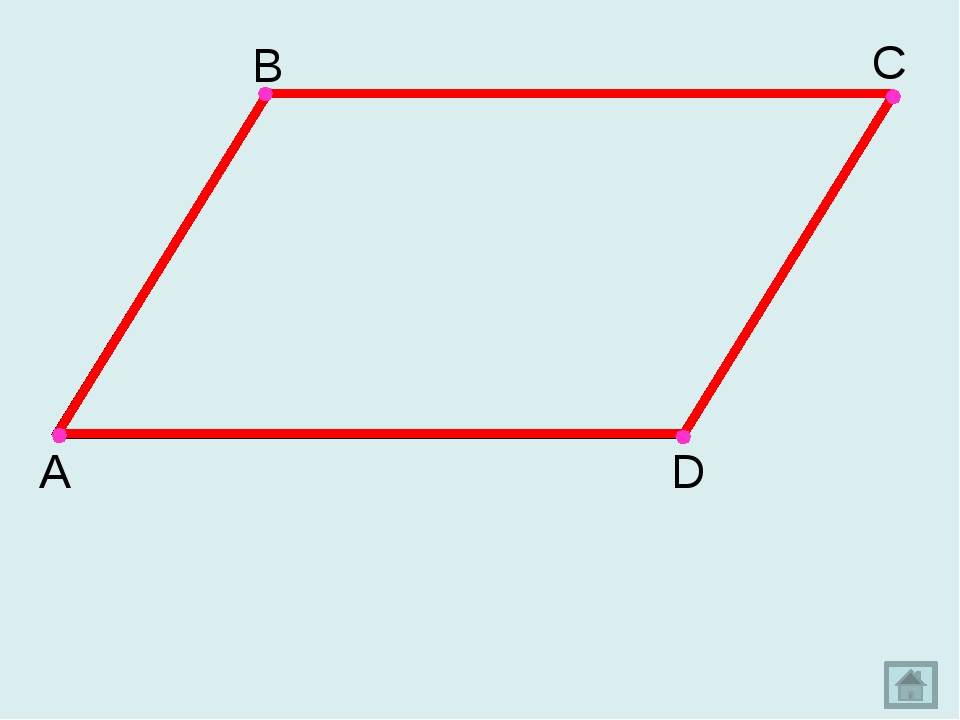 мы все
испытали идеальную песню в идеальное время и знают, как
электрифицировать это может быть. набор и настройка, которые объединяются, чтобы сделать те
выбор музыкального автомата, микс-кассеты или плейлисты действительно работают может быть так сложно определить, но легко идентифицировать, когда они там
в дикой природе. часть веселья за шторами в трехлопастном
записи всегда пытались угадать алхимию пар
которые работают до наших ушей. эти усилия снова и снова принимали форму
коллекций и коллабораций, как в виде многотомных выпусков
(от тройки многодисковых компакт-дисков до не
пробелы вы знаете, но между ними бокс-сет) и отдельные альбомы (например, совместные альбомы из
золотой ганн или группа хагерти-тот
к восьмерке тропы, одна тропа сборник).Имея это в виду, Three lobed с гордостью представляет параллелограмм ,
сборник из пяти тщательно составленных сплит-альбомов, посвященных
дополнительные музыкальные пары.
мы все
испытали идеальную песню в идеальное время и знают, как
электрифицировать это может быть. набор и настройка, которые объединяются, чтобы сделать те
выбор музыкального автомата, микс-кассеты или плейлисты действительно работают может быть так сложно определить, но легко идентифицировать, когда они там
в дикой природе. часть веселья за шторами в трехлопастном
записи всегда пытались угадать алхимию пар
которые работают до наших ушей. эти усилия снова и снова принимали форму
коллекций и коллабораций, как в виде многотомных выпусков
(от тройки многодисковых компакт-дисков до не
пробелы вы знаете, но между ними бокс-сет) и отдельные альбомы (например, совместные альбомы из
золотой ганн или группа хагерти-тот
к восьмерке тропы, одна тропа сборник).Имея это в виду, Three lobed с гордостью представляет параллелограмм ,
сборник из пяти тщательно составленных сплит-альбомов, посвященных
дополнительные музыкальные пары.
пары, содержащиеся в параллелограмм коллекции принимают несколько различных форм. родственные ли артисты духи, бывшие партнеры по гастролям и / или люди, которые взаимно вдохновляли друг друга, материал на каждой стороне каждого из записи естественным образом перекачиваются в другие. в целом художники собрали как параллелограмм служат своего рода отражением жанров и стилей, встречающихся в полнота трехлопастного каталога.
параллелограмм Коллекция состоит из следующих пяти альбомов:
шипение золотой посланник / Майкл Чепмен (TLR-109)
шесть органов приема / Уильям Тайлер (TLR-110)
курт вайл / стив ганн (TLR-111)
Терстон Мур и Джон Молони: записано на пленку / [алан] епископ — оркатт — Корсано трио (TLR-112)
пруд бардо / йо ла тенго (TLR-113)
каждый альбом состоит из никогда ранее выпущенный материал составлен специально с этим сборником в разум.каждый LP будет помещен в отдельную букву, нажатую «Спичечный коробок» (по своей природе похожий на те, что используются на восемь троп, одна тропа сборник гитары [TLR-091]) с новым оригинальным оформлением Кейси ожоги и напечатаны ловкостью пресса. каждая пластинка нажата на 140 г черного винил, отпечатанный на звукозаписывающей индустрии в Нидерландах, и включает в себя скачать купон. все 5 пластинок мастерил Патрик Клем. все 5 пластинок отправим одновременно в одной упаковке.
пару лет в создание, эта коллекция представляет собой празднование этого невероятное пятнадцатилетие лейбла.показалось уместно собрать столь же невероятный проект, чтобы отпраздновать веха. нам не терпится поделиться этой коллекцией со всеми вами.
всего примерно 950 пять LP коллекции доступны с трехлопастными. параллелограмм коллекцию можно купить только с трехлопастной, так как установлена пятикратная и не по меню. у всех участвующих художников будет отдельные копии соответствующих альбомов для продажи позже по их собственным каналам.
(обновлено 7 февраля 2016 г.).
iä! шуб-ниггурат!
ПАРАЛЛЕЛОГРАММА, дерево, художественный принт
Принимаются все основные кредитные карты и подарочные карты Etsy.
Товары будут отправлены в течение 1-3 рабочих дней, если иное не указано в описании (т. Е. Сделано на заказ или с задержкой заказа). Товары будут отправлены почтой первого класса USPS, если они не будут повышены до уровня Priority во время оформления заказа. Когда он будет к вам, вам будет отправлен номер для отслеживания! Свяжитесь с нами для срочной доставки.
Не несет ответственности за утерянную или украденную почту. Убедитесь, что вы правильно ввели адрес. Мы не будем покрывать расходы на товары, которые возвращаются нам для повторной отправки. Ответственность за повторную отправку товара несет покупатель.
Обмен и возврат
Я с радостью принимаю возврат, обмен и отмену
Просто свяжитесь со мной в течение: 3 дней с момента доставки
Отправьте мне товары в течение: 7 дней с момента доставки
Запросить отмену в течение: 1 часа с момента покупки
Но, пожалуйста, свяжитесь со мной, если у вас возникнут проблемы с вашим заказом.
Следующие предметы не подлежат возврату или обмену
Из-за характера этих предметов, если они не будут доставлены поврежденными или дефектными, я не могу принять возврат за:
- Индивидуальный или индивидуальный заказ
- Товаров в продаже
Есть вопросы по вашему заказу?
Свяжитесь со мной, если у Вас возникнут проблемы с заказом.
Реквизиты для возврата и обмена
В том маловероятном случае, если вы получите товар с проблемой, пожалуйста, свяжитесь с нами в течение трех дней с момента получения доставки, мы поможем вам решить эту проблему!
Мы принимаем возврат неоткрытых предметов.Предметы должны быть неиспользованными и в отличном состоянии. Ответственность за обратную доставку несет покупатель. Стоимость доставки не возвращается. Если ваш заказ был отправлен с БЕСПЛАТНОЙ ДОСТАВКОЙ, расходы, понесенные нами за эту доставку, не будут возвращены. В среднем это стоит от 5 до 10 долларов США. Не стесняйтесь спрашивать, рассматриваете ли вы стоимость возврата. Я буду рад найти для вас квитанцию об отгрузочной этикетке.
В случае, если ваша посылка будет повреждена, необходимо своевременно подать заявку на страхование.Пожалуйста, свяжитесь с нами как можно скорее. Обязательно храните товар (-ы) в коробке в том виде, в котором он был получен, с видимыми повреждениями. Грузоотправителю потребуется документация. Спасибо!
Скачать бесплатно файл STL Площадь параллелограмма • Объект для 3D-печати ・ Культы
?Творческое качество: 0,0 / 5 (0 голосов)
Оценка участников по пригодности для печати, полезности, уровню детализации и т. Д.
Ваш рейтинг: 0/5 Удалить
Ваш рейтинг: 0/5
- 👁 1,3 км Просмотры
- 2 нравится
- 21 год загрузки
Описание 3D модели
Докажите себе, что площадь параллелограмма равна основанию, умноженному на высоту.
Вот обзорное видео:
Предоставляются три набора пазлов. Каждый набор может быть скомпонован так, чтобы образовать один и тот же прямоугольник, и перегруппирован, чтобы образовать разные параллелограммы с одинаковой площадью.
Учителя: Предложите учащимся следовать Руководству по исследованию (файл в формате pdf). Он задает несколько хороших вопросов, чтобы заставить их думать математически.
Вот стандарты Common Core, связанные с этой манипуляцией: 3.MD.5, 3MD.8 и 4.MD.3
Я включил исходные файлы (SketchUp) в zip-архив.
Настройки 3D-печати
Распечатайте базовый контейнер и три набора головоломок и следуйте руководству по исследованию.
Вот цвета, которые я использовал в видео:
ЧЕРНЫЙ: базовый контейнер (с белым текстом, см. Ниже)
ОРАНЖЕВЫЙ: набор пазлов A
ЖЕЛТЫЙ: набор пазлов B
ЗЕЛЕНЫЙ: набор пазлов C
У меня нет двойной экструзии на моем принтере, поэтому, чтобы получить белое на черном для контейнера, я начал с черного, затем приостановил печать на 4 мм и переключился на белую нить.С нетерпением жду возможности скоро научиться делать файлы двойной экструзии.
Примечание: Если набор головоломок C не подходит, попробуйте альтернативную версию.
Информация о файле 3D-принтера
- Формат 3D-дизайна : STL и ZIP
Детали папки
Закрывать
- Base_Container.stl
- PuzzleSet_A.stl
- PuzzleSet_B.stl
- PuzzleSet_C.stl
- PuzzleSet_C_Alternate.stl
- SourceFile.zip
Подробнее о форматах
- Дата публикации : 2018.11.29 в 15:26
Лицензия
CCBYSA
Теги
Создатель
Бестселлеры категории Разное
Хотели бы вы поддержать культы?
Вы любите Культы и хотите помочь нам продолжить приключение самостоятельно ? Обратите внимание, что мы небольшая команда из 3 человек , поэтому очень просто поддержать нас поддерживать активность и создавать будущие разработки .Вот 4 решения, доступные всем:
РЕКЛАМА: Отключите блокировщик баннеров AdBlock и нажимайте на наши рекламные баннеры.
ПРИСОЕДИНЕНИЕ: Делайте покупки в Интернете, нажимая на наши партнерские ссылки здесь Amazon или Aliexpress.
ПОЖЕРТВОВАТЬ: Если хотите, вы можете сделать пожертвование через PayPal здесь.
СЛОВО РТА: Пригласите своих друзей прийти, откройте для себя платформу и великолепные 3D-файлы, которыми поделились сообщество!

 А каков признак прямоугольника? Закончите предложение: параллелограмм – прямоугольник, если…
А каков признак прямоугольника? Закончите предложение: параллелограмм – прямоугольник, если…
 Посмотрите внимательно на квадрат и давайте дадим ему определение. Закончите предложения: 1) квадрат – ромб, у которого…; 2)квадрат – прямоугольник, у которого …
Посмотрите внимательно на квадрат и давайте дадим ему определение. Закончите предложения: 1) квадрат – ромб, у которого…; 2)квадрат – прямоугольник, у которого …
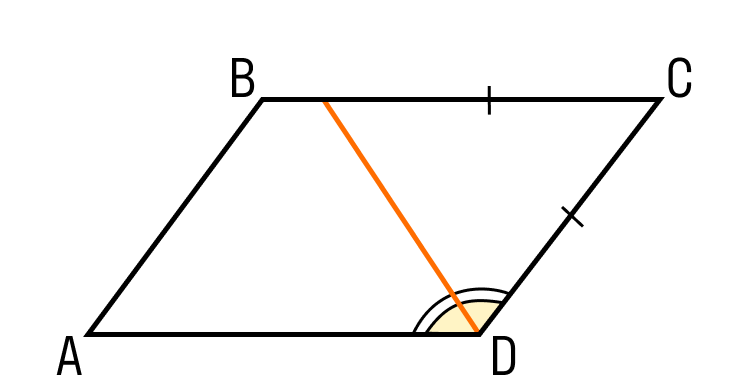

 Дан
ромб KLMN, в котором a = 35°.
Выберите правильное утверждение.
Дан
ромб KLMN, в котором a = 35°.
Выберите правильное утверждение.