Отличие диаграммы от графика: Графики против диаграмм | Лучшие 6 отличий для изучения (с инфографикой)

Содержание

Графики против диаграмм | Лучшие 6 отличий для изучения (с инфографикой)

Разница между графиками и графиками
Графики и диаграммы являются почти схожей терминологией и широко используются корпорациями или в любых других деловых предложениях, презентациях для различных целей и т. Д. Для представления чисел, отчетов или результатов и т. Д. График — это тип диаграммы и математическая функция, которая также можно использовать диаграмму данных, которая является статистической. Диаграмма, показывающая соотношение между переменными величинами, обычно 2 переменными, и где каждая из них будет измеряться вдоль 1 пары осей под прямым углом. С другой стороны, диаграмма — это форма графического представления данных, где линейная диаграмма является одним из видов формы. Диаграмма действительно представляет числовые данные в виде таблицы, а также может представлять функции или некоторый тип качественной структуры и может предоставлять различную информацию.
Сравнение лицом к лицу между графиками и диаграммами (инфографика)
Ниже представлено 6 лучших отличий между графиками и графиками.
Ключевые отличия графиков от диаграмм
Оба графика против диаграмм являются популярным выбором на рынке; давайте обсудим некоторые основные различия между графиками и диаграммами
Основное ключевое различие между графиками и диаграммами заключается в том, что граф представляет собой тип диаграммы, которая будет представлять систему взаимосвязей или связей между двумя или более чем двумя вещами несколькими отличительными линиями, точками, столбцами и т. Д., А диаграмма как Ранее указывалось, что это тип графического представления информации или данных, в которых «данные, которые представлены символами, такими как линии на линейной диаграмме, столбцы на гистограмме или срезы на круговой диаграмме».
Графики — это подмножество диаграмм, так как диаграммы — их большая версия.
Графики представляют математические связи или взаимосвязи между различным набором данных, тогда как диаграммы представляют диаграммы, где можно найти изображенную информацию или данные.
Как упоминалось ранее, все типы графиков являются диаграммами, но, с другой стороны, не все диаграммы являются графиками.
Диаграммы — это большая группа методов для изображения или представления данных или информации, в то время как графики предоставляют один из тех методов (которые диаграммы используют для представления информации), представляя данные в визуальном формате.
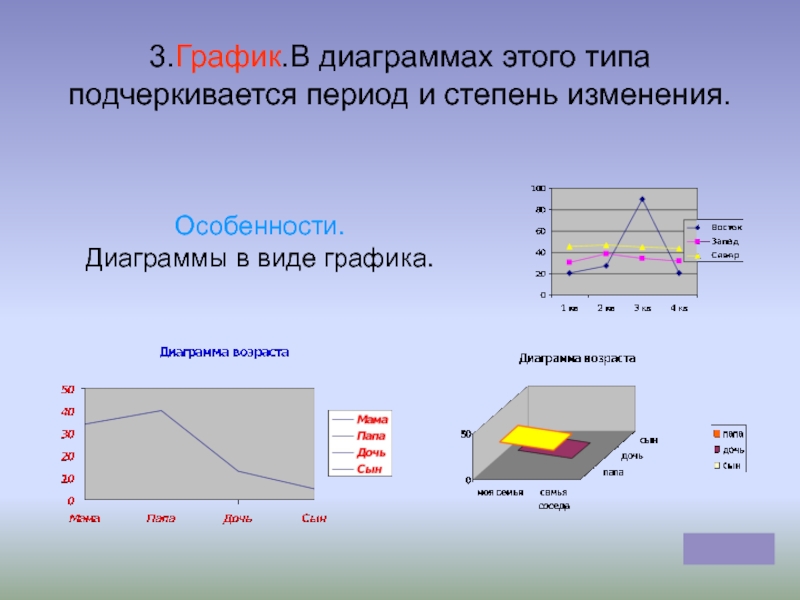
Диаграмма будет иллюстрировать информацию или данные с использованием только одной количественной координаты, тогда как с другой стороны график представляет собой тип метода привязки одной качественной переменной к другой количественной переменной и, как правило, ее времени.
Сравнительная таблица графиков и графиков
Ниже приведено 6 лучших сравнений графиков и графиков.

Основа сравнения графиков с графиками
диаграммы
Графики
Основное определение График представляет собой вид диаграммы, которая представляет собой систему взаимосвязей или связей между двумя или более вещами несколькими отличительными линиями, точками, полосами и т.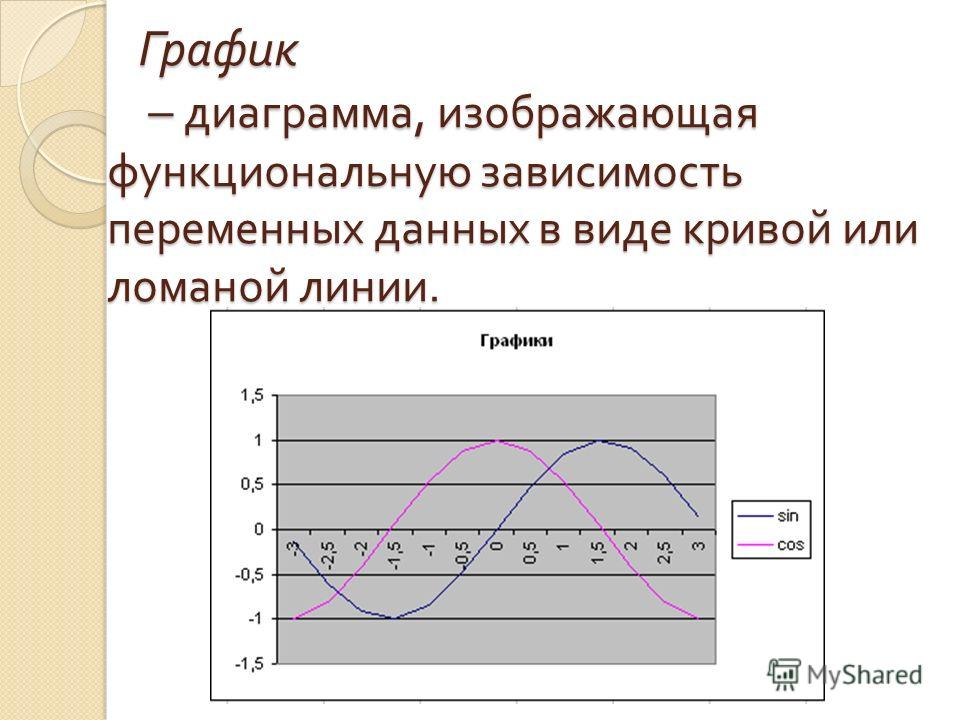 Д. Диаграмма — это вид графического представления данных, в котором «данные, которые представлены символами, такими как линии на линейной диаграмме, столбцы на гистограмме или срезы на круговой диаграмме».
Представление Графики покажут математические связи или взаимосвязь между наборами данных. Графики будут представлять информацию или данные в виде диаграмм, графиков или таблиц.
Они такие же? Все виды графиков являются диаграммами; следовательно, графики являются одним из видов диаграмм. Все виды графиков не являются графиками.
Сфера Графики также предоставляют визуальную форму, используя один из этих методов (то есть большую группу диаграмм), представляя данные в визуализированном формате. Диаграммы — это большая группа методов, которые используются для представления данных или информации.
Что они делают? Графики сделают фотографии из числовых данных или числовой информации.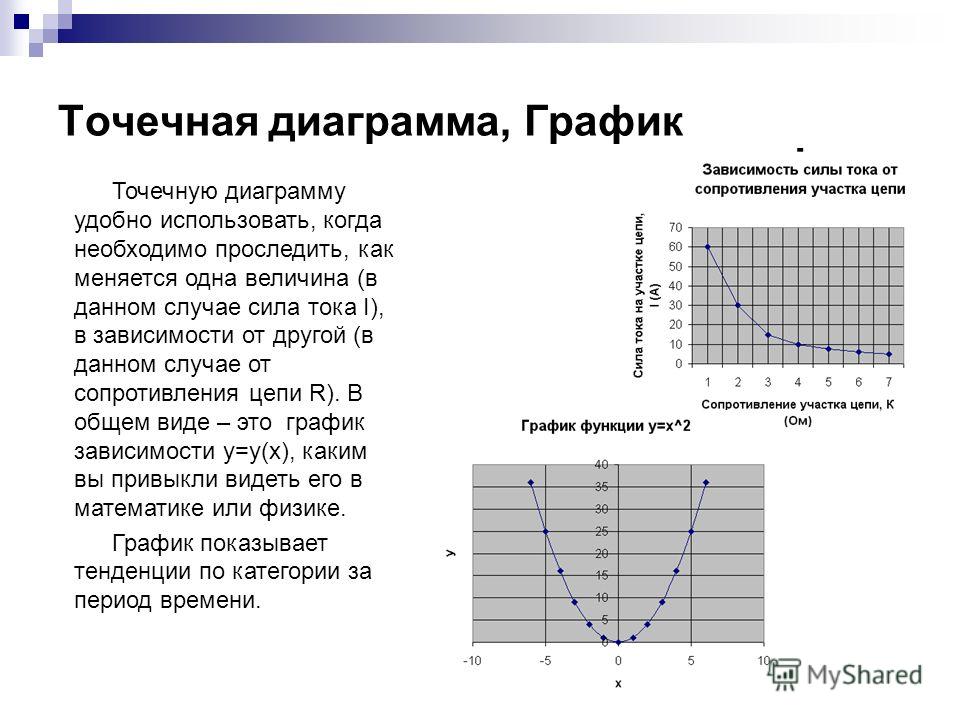 Диаграммы, которые используются в диаграммах, могут показать последовательные события, такие как история рекомендаций правительства США по питанию или цикл горных пород.
Их типы Круговые диаграммы, гистограммы, линейные графики и т. Д. Являются типами графиков и используются для различных целей. Как указывалось ранее, графики являются подмножеством диаграмм, и, следовательно, диаграммы не имеют своего собственного типа, но, тем не менее, существуют примеры диаграмм, например, использование карт для включения статистики вождения в нетрезвом виде или местоположений вулканов и землетрясений.
Вывод — графики против диаграмм
Графики являются одними из наиболее подходящих для количественного сравнения групп данных или отдельных категорий. Самые популярные диаграммы — это столбцы, столбцы, линии и круговые диаграммы. Гистограмма будет особенно полезна для отображения информации или данных о поле, профессии, этнической принадлежности, типах выписок и категориях лечения.
Гистограммы полезны или подходят для отображения категориальной информации или категориальных данных. Гистограммы будут сравнивать группы или категории, используя некоторые количественные измерения.
Графики, с другой стороны, могут быть простыми, или они могут оказаться довольно сложными, но они должны всегда выбираться так, чтобы представлять свою информацию или данные как можно более четко. Иногда 2 графика могут быть лучше, чем один график, если каждый из графиков показывает различные аспекты одного и того же набора информации или набора данных. Однако не все графики, которые созданы равными. Тип графика, который будет использоваться, будет зависеть от типа набора данных.

Большинство общих графиков, которые используются: это гистограммы и частотные полигоны. Количественные непрерывные данные могут быть отображены в виде графика.
Графики предназначены для случаев, когда есть одна качественная переменная (например, тип, пол или предпочтение) и 1 количественная переменная (например, возраст, время или количество).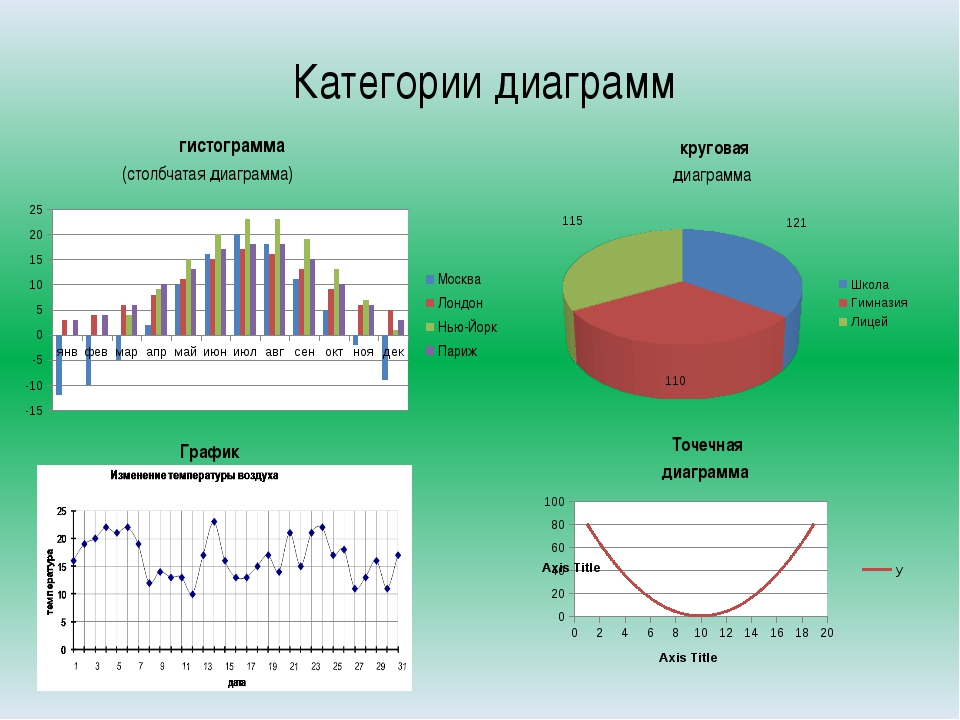
Они должны включать гистограммы и круговые диаграммы. Принимая во внимание, что графики для, когда есть 2 количественных переменных.
Можно не найти графики в следующих видах диаграмм.
График тестирования глаз
Диаграмма поиска
Круговая диаграмма
Рекомендуемые статьи
Это было руководство к разнице между графиками и диаграммами. Здесь мы также обсудим ключевые отличия графиков от диаграмм с помощью инфографики и сравнительной таблицы. Вы также можете взглянуть на следующие статьи, чтобы узнать больше
Разница между начислением и обеспечением
Запас против инвентаря — какой лучше
Цена предложения против цены предложения
Как сравнить День против Свинг-трейдинга?
Представление данных в виде точечной диаграммы или графика
Основное различие между точечная и графиками заключается в способе их отстройки на горизонтальной оси. Например, если использовать следующие данные листа для построения точечной диаграммы и графика, они будут представлены по-разному:

На точечной диаграмме значения суточного количества осадков из столбца A отображаются в виде значений X на горизонтальной оси (X), а показатели содержания твердых частиц из столбца B — в виде значений на вертикальной оси (Y). На точечной диаграмме категории никогда не отображаются на горизонтальной оси.

На точечной диаграмме всегда есть две оси значений, то есть один набор числовых данных представлен вдоль горизонтальной оси, а другой — вдоль вертикальной. На пересечении координат X и Y отображается точка данных, объединяющая эти два числовых значения. Такие точки данных могут быть распределены по горизонтальной оси равномерно или неравномерно, в зависимости от конкретных данных.

Первая точка данных на точечной диаграмме представляет значение Y (содержание частиц), равное 137, и значение X (суточная норма осадков), равное 1,9. Эти числа представляют значения в ячейках A9 и B9 на листе.
На графике те же значения суточного количества осадков и содержания частиц будут показаны как две разные точки данных, которые равномерно распределяются вдоль горизонтальной оси. Дело в том, что на графике есть только одна ось значений (вертикальная ось).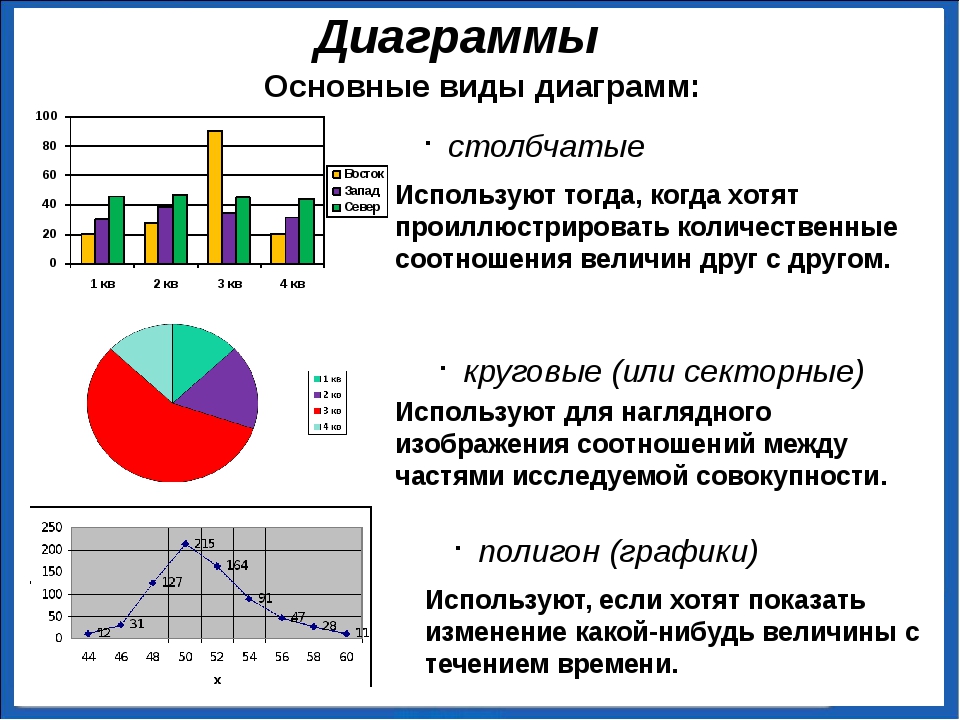 Горизонтальная ось графика предназначена для отображения группировок (категорий) данных с равномерными интервалами. Так как категории не были заданы, они генерируются автоматически, например 1, 2, 3 и т. д.

Это наглядный пример ситуации, когда график использовать не следует.

На графиках данные категории равномерно распределяются вдоль горизонтальной оси (оси категорий), а все числовые значения откладываются по вертикальной оси (оси значений).
Значение Y (содержание частиц), равное 137 (ячейка B9), и значение X (суточное количество осадков), равное 1,9 (ячейка A9), показаны на графике двумя разными точками данных. Ни одна из этих точек данных не является первой точкой данных, отображаемой на диаграмме. Вместо этого первая точка данных для каждого значения ряд данных ссылается на значения в первой строке данных на этом сайте (ячейки A2 и B2).

Различия между типами и шкалами осей
Так как горизонтальная ось точечной диаграммы всегда является осью значений, на ней можно показывать числа и даты (в том числе дни и часы), представляемые в виде числовых значений. Чтобы отображать числовые значения вдоль горизонтальной оси с большей гибкостью, можно изменить параметры ее шкалы аналогично тому, как изменяется настройка шкалы вертикальной оси.

Поскольку горизонтальная ось графика — это ось категорий, она может быть только осью текста или осью дат. На оси текста отображается только текст (нечисловые данные или числовые категории, не являющиеся значениями) с равномерными интервалами. На оси дат отображаются даты в хронологическом порядке через заданные интервалы (базовые единицы измерения), такие как число дней, месяцев или лет, даже если даты на листе расположены в ином порядке или выражены в других единицах.
Набор параметров шкалы оси категорий ограничен по сравнению с параметрами шкалы оси значений. Доступные параметры шкалы также зависят от типа используемой оси.

Графические методы анализа данных

Графические методы анализа данных
Графические методы анализа данных

Краткий обзор типов графиков

Типичные методы визуализации

Категоризованные графики

Одним из наиболее мощных аналитических методов исследования является разделение («разбиение») данных на группы для сравнения структуры получившихся подмножеств.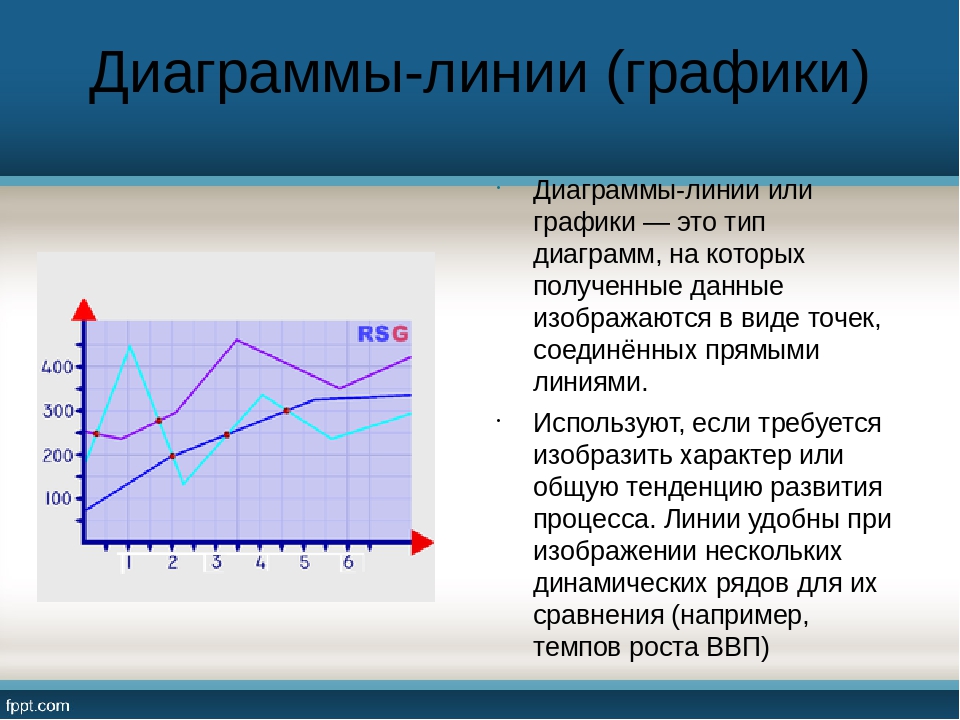 Эти методы широко применяются как в разведочном анализе данных, так и при проверке гипотез и известны под разными названиями (

классификация, группировка, категоризация, разбиение, расслоение и пр.). Например, взаимосвязь между возрастом и риском инфаркта может отличаться для мужчин и женщин (для мужчин эта зависимость сильнее). Или например, зависимость между приемом лекарств и снижением уровня холестерина может наблюдаться только для женщин с пониженным давлением и в возрасте 30-40 лет. Производительность или гистограммы мощности могут различаться для временных промежутков, когда управление осуществляется разными операторами. Разным экспериментальным группам также могут соответствовать разные наклоны линий регрессии.

Для количественного описания различий между группами наблюдений разработаны многочисленные вычислительные методы, основанные на группировке данных (например, дисперсионный анализ). Однако графические средства (такие как рассматриваемые в этом разделе категоризованные графики) дают особые преимущества и позволяют выявить закономерности, которые трудно поддаются количественному описанию и которые весьма сложно обнаружить с помощью вычислительных процедур (например, сложные взаимосвязи, исключения или аномалии). В этих случаях графические методы предоставляют уникальные возможности многомерного аналитического исследования или «добычи» данных.

Что такое категоризованные графики

Термин «категоризованные графики» впервые был использован в программе STATISTICA компании StatSoft в 1990 году (кроме того, Becker, Cleveland и Clark из Bell Labs называют их графиками на решетке). Эти графики представляют собой наборы двумерных, трехмерных, тернарных или n-мерных графиков (таких как гистограммы, диаграммы рассеяния, линейные графики, поверхности, тернарные диаграммы рассеяния и пр.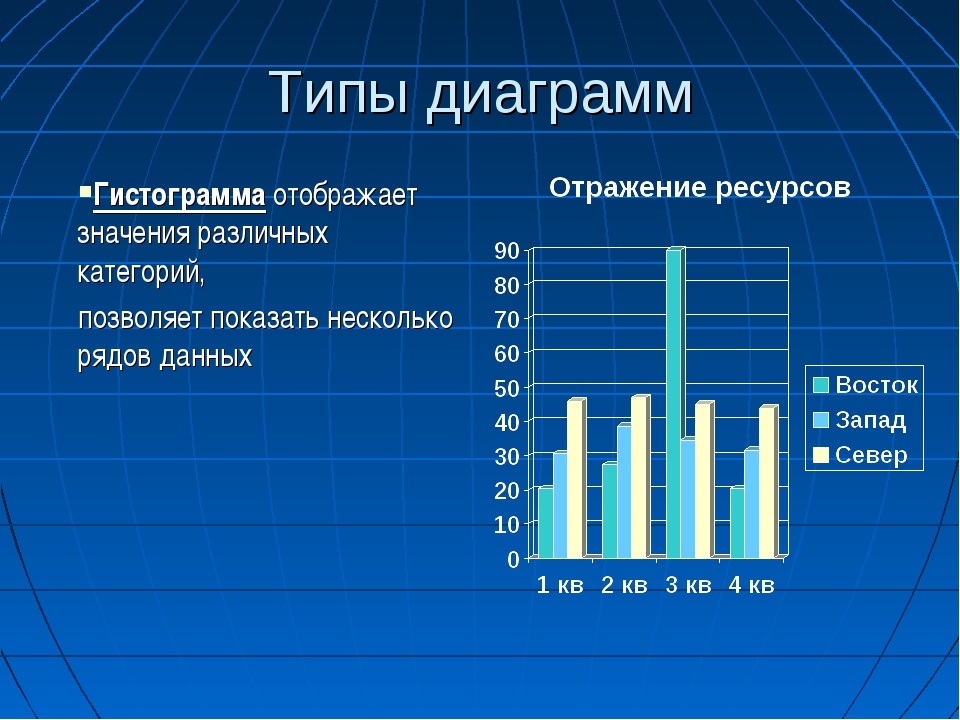 ), по одному графику для каждой выбранной категории (подмножества) наблюдений, например, опрашиваемых из Нью-Йорка, Чикаго или Далласа. Эти «входящие» графики располагаются последовательно в одном графическом окне, позволяя сравнивать структуру данных для каждой из указанных подгрупп (например, городов).

Для выбора подгрупп можно использовать множество методов, самый простой из них — это введение категориальной переменной (например, переменной City с значениями New York, Chicago и Dallas). На следующем графике показаны гистограммы переменной, представляющей данные о самооценке стресса жителями каждого из трех городов.

На основе этих данных можно сделать вывод о том, что жители Далласа не очень подвержены стрессам, в то время как распределения уровня стресса в Нью-Йорке и Чикаго довольно похожи.

Некоторые программы (например, система STATISTICA) поддерживают двухвходовую или многомерную категоризацию, где для задания подгрупп используется не один (например, City), а два или более критериев (например, City и Time ).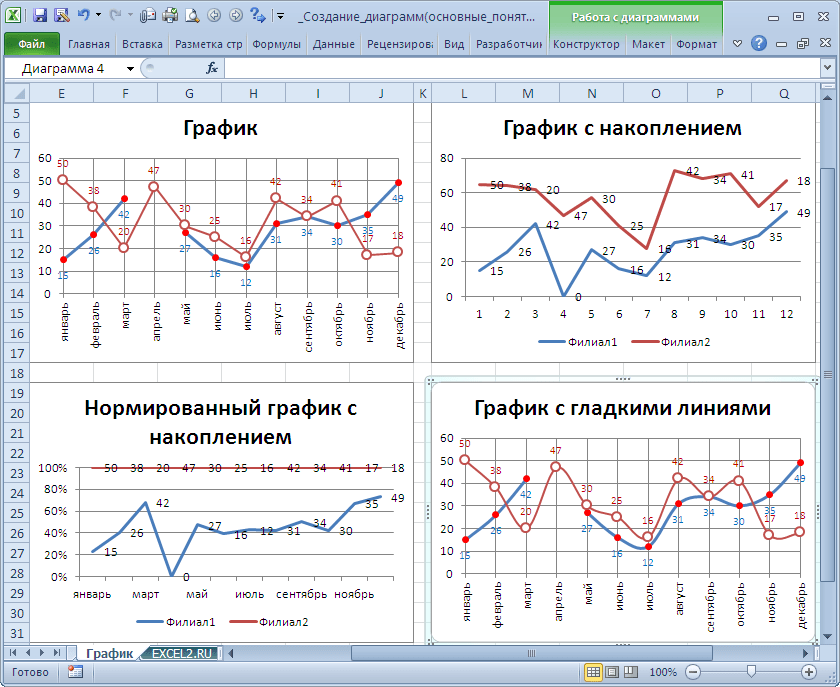 Двухвходовые категоризованные графики можно рассматривать как «таблицы графиков», где каждый входящий график находится на «пересечении» определенных значений первой (например, City) и второй (например, Time) группирующих переменных.

Добавление второго фактора показывает, что картины стрессовых нагрузок в Нью-Йорке и Чикаго в действительности сильно различаются, если учитывается время опроса, в то время как фактор времени практически ничего не меняет в Далласе.

Категоризованные и матричные графики. Матричные графики также состоят из нескольких графиков; однако здесь каждый из них основывается (или может основываться) на одном и том же множестве наблюдений, и графики строятся для всех комбинаций переменных из одного или двух списков. Для категоризованных графиков требуется такой же выбор переменных, как и для некатегоризованных графиков соответствующего типа (например, две переменных для диаграммы рассеяния). В то же время для категоризованных графиков необходимо указать по крайней мере одну группирующую переменную (или способ разбиения наблюдений на категории), где содержалась бы информация о принадлежности каждого наблюдения к определенной подгруппе (например, Chicago, Dallas). Группирующая переменная не будет непосредственно изображена на графике (т.е. не будет построена), однако она будет служить критерием для разделения всех анализируемых наблюдений на отдельные подгруппы. Как показано выше, для каждой группы (категории), определяемой группирующей переменной, будет построен один график.

Общие и независимые шкалы. Каждый элементарный график, входящий в состав категоризованного графика, может быть масштабирован в соответствии со своим собственным диапазоном значений (независимые шкалы).

Или все графики могут иметь общую шкалу, достаточно широкую, чтобы охватить весь диапазон значений.

Общий масштаб позволяет сравнивать диапазоны и распределения значений разных категорий. Однако, если эти диапазоны сильно различаются (что приводит к очень большой общей шкале), то исследование некоторых графиков может быть затруднено. Использование независимого масштаба может упростить выявление трендов и определенных закономерностей внутри категорий, но в то же время затруднить сравнение диапазонов значений разных подгрупп.

Методы категоризации

Существует пять основных методов категоризации значений, которые будут кратко описаны в этом разделе: целые числа, категории, границы, коды и сложные подгруппы. Обратите внимание, что одни и те же методы категоризации можно использовать как для разбиения наблюдений по входящим графикам, так и для категоризации наблюдений внутри входящих графиков ( например, на гистограммах или диаграммах размаха).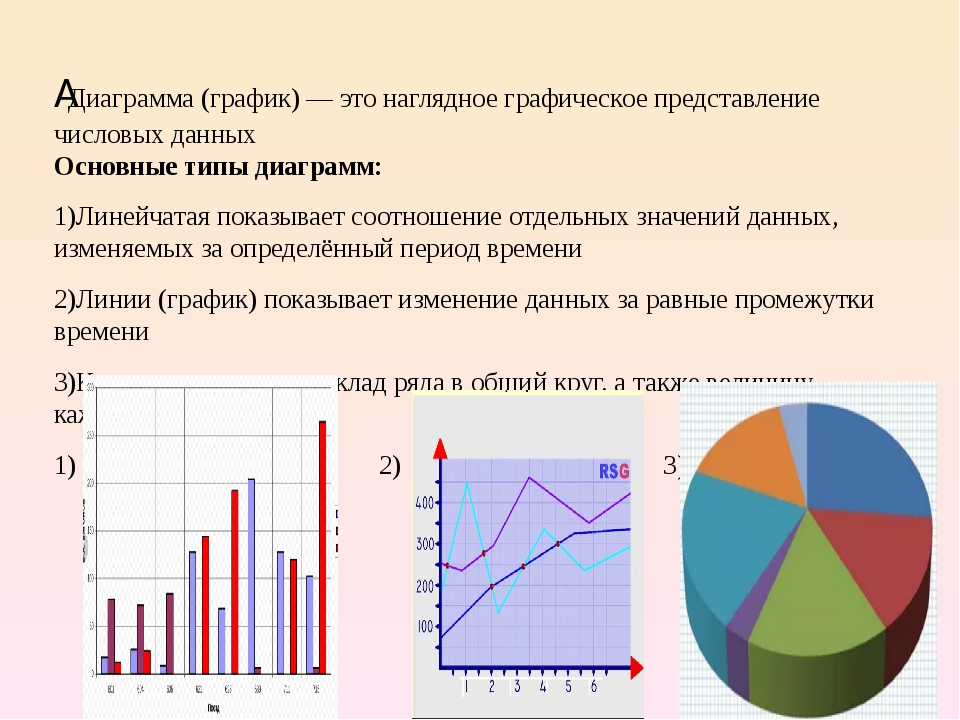

Целые числа. При использовании этого режима для определения категорий будут использованы целые значения выбранной группирующей переменной, и для всех наблюдений, принадлежащих каждой категории (заданной этими целыми числами), будет построено по одному графику. Если выбранная группирующая переменная содержит не целочисленные значения, то программа автоматически округлит каждое значение выделенной переменной до целого числа.

Категории. В этом режиме категоризации нужно указать желаемое число категорий. Программа разделит весь диапазон значений выбранной группирующей переменной (от минимального до максимального) на указанное число интервалов равной длины.

Границы. Метод границ также представляет собой интервальную категоризацию, однако в этом случае интервалы могут иметь произвольную (например, различную) длину, определяемую пользователем (например, «меньше -10», «больше или равно -10, но меньше 0», «больше или равно 0, но меньше 10» и «больше или равно 10»).

Коды. Этот метод следует использовать в том случае, если выбранная группирующая переменная содержит «коды » (т.е. особые смысловые значения, такие как Male, Female), по которым можно разбить данные на категории.

Сложные подгруппы. Этот метод дает возможность пользователю использовать для выделения подгрупп более одной переменной. Другими словами, категоризация, основанная на выделении сложных подгрупп, может представлять не распределения конкретных переменных, а распределения частот определенных «событий» при заданной комбинации значений любого числа переменных текущего набора данных. Например, можно указать шесть категорий, задаваемых комбинациями значений трех переменных Gender, Age и Employment.

Гистограммы

Гистограммы используются для изучения распределений частот значений переменных. Такое частотное распределение показывает, какие именно конкретные значения или диапазоны значений исследуемой переменной встречаются наиболее часто, насколько различаются эти значения, расположено ли большинство наблюдений около среднего значения, является распределение симметричным или асимметричным, многомодальным (т.е. имеет две или более вершины) или одномодальным и т.д. Гистограммы также используются для сравнения наблюдаемых и теоретических или ожидаемых распределений.

Категоризованные гистограммы представляют собой наборы гистограмм, соответствующих различным значениям одной или нескольких категоризующих переменных или наборам логических условий категоризации (см. Методы категоризации).

Частотные распределения могут представлять интерес по двум основным причинам.
По форме распределения можно судить о природе исследуемой переменной (например, бимодальное распределение позволяет предположить, что выборка не является однородной и содержит наблюдения, принадлежащие двум различным множествам, которые в свою очередь нормально распределены).

Многие статистики основываются на определенных предположениях о распределениях анализируемых переменных; гистограммы позволяют проверить, выполняются ли эти предположения.

Как правило, работа с новым набором данных начинается с построения гистограмм всех переменных.

Гистограммы и группировка. Категоризованные гистограммы предоставляют такую же информацию о данных, как и группировка (например, среднее, медиану, минимум, максимум, разброс и т.п.; см. главу Основные статистики и таблицы). Хотя конкретные (числовые) значения описательных статистик легко увидеть в таблице, в то же время общую структуру и глобальные характеристики распределения проще изучать на графике. Более того, график дает качественную информацию о распределении, которую невозможно отразить с помощью какого-либо одного параметра. Например, по асимметрии распределения значений дохода можно сделать вывод о том, что большинство населения имеет низкий, а не высокий уровень доходов. Если помимо этого провести группировку данных по этническому и половому признакам, то можно обнаружить, что в некоторых подгруппах эта структура распределения станет еще более ярко выраженной. Хотя эта информация содержится в значении коэффициента асимметрии (для каждой подгруппы), но она легче воспринимается и запоминается, будучи графически представленной на гистограмме. Кроме того, на гистограмме можно наблюдать некоторые «впадины и выпуклости», которые могут свидетельствовать о социальном расслоении в исследуемой группе населения или об аномалиях в распределении дохода отдельных подгрупп, связанных с недавней налоговой реформой.

Категоризованные гистограммы и диаграммы рассеяния. Полезное применение категоризации для непрерывных переменных — это представление взаимосвязи трех переменных одновременно. Ниже показана диаграмма рассеяния для двух переменных Load 1 и Load 2.

Предположим, к ним нужно добавить третью переменную (Output) и исследовать ее распределение при различных значения совместного распределения переменных Load 1 и Load 2. Для этого можно построить следующий график:

На этом графике обе переменные Load 1 и Load 2 сгруппированы в 5 интервалов, и для каждой комбинации этих интервалов вычислено распределение переменной Output. Обратите внимание, что внутри «прямоугольника» (параллелограмма) находятся наблюдения, одинаковые для обоих показанных выше графиков.

Диаграммы рассеяния

Двумерные диаграммы рассеяния используются для визуализации взаимосвязей между двумя переменными X и Y (например, весом и ростом). На этих диаграммах отдельные точки данных представлены маркерами на плоскости, где оси соответствуют переменным. Две координаты (X и Y), определяющие положение точки, соответствуют значениям переменных. Если между переменными существует сильная взаимосвязь, то точки на графике образуют упорядоченную структуру (например, прямую линию или характерную кривую). Если переменные не взаимосвязаны, то точки образуют «облако».

Можно построить также категоризованные диаграммы рассеяния, сгруппированные по значениям одной или нескольких переменных, а с помощью метода сложных подгрупп (см. Методы категоризации) — диаграммы рассеяния, категоризованные по заданным логическим условиям выбора подгрупп наблюдений.

Категоризованные диаграммы рассеянияпредставляют собой мощный исследовательский и аналитический метод для изучения взаимосвязей между двумя и более переменными среди различных подгрупп.

Однородность двумерных распределений (форма взаимосвязей).Диаграммы рассеяния обычно используются для выявления природы взаимосвязи двух переменных (например, кровяного давления и уровня холестерина), поскольку они предоставляют гораздо больше информации, чем коэффициент корреляции.

Например, неоднородность выборки, по которой рассчитываются корреляции, может привести к искажению значений коэффициента корреляции. Предположим, коэффициент корреляции рассчитывается по данным, полученным в двух экспериментальных группах, но этот факт при вычислениях игнорируется. Пусть эксперимент в одной из подгрупп привел к увеличению значений обеих переменных, и на диаграмме рассеяния данные из каждой группы образуют отдельные «облака» (как показано на картинке).

В этом примере большое значение коэффициента корреляции целиком обусловлено распределением по группам и не отражает «истинную» взаимосвязь между двумя переменными, которая практически близка к 0 (это хорошо видно, если рассматривать каждую группу отдельно).

Если вы предполагаете, что подобная структура присутствует и в ваших данных, и знаете, каким образом выделить «подгруппы» наблюдений, то имеет смысл построить категоризованную диаграмму рассеяния.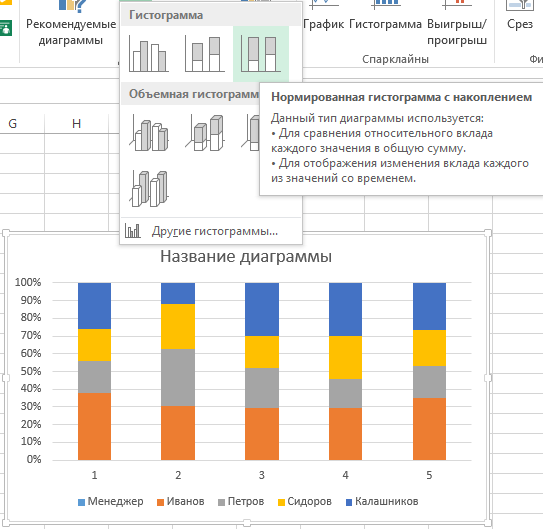

Такой график поможет вам прояснить структуру взаимосвязей между переменными X и Y внутри каждой подгруппы (после соответствующего разбиения наблюдений).

Нелинейные зависимости. С помощью диаграмм рассеяния можно исследовать и нелинейные взаимосвязи между переменными. При этом не существует каких-либо «автоматических» или простых способов оценки нелинейности. Стандартный коэффициент корреляции Пирсона r позволяет оценить только линейность связи, а некоторые непараметрические корреляции, например, Спирмена R, дают возможность оценить нелинейность, но только для монотонных зависимостей. На диаграммах рассеяния можно изучить структуру взаимосвязей, чтобы затем с помощью преобразования привести данные к линейному виду или выбрать подходящую нелинейную подгонку.

Дополнительную информацию можно найти в разделах Основные статистики, Непараметрическая статистика и распределения, Множественная регрессия и Нелинейное оценивание.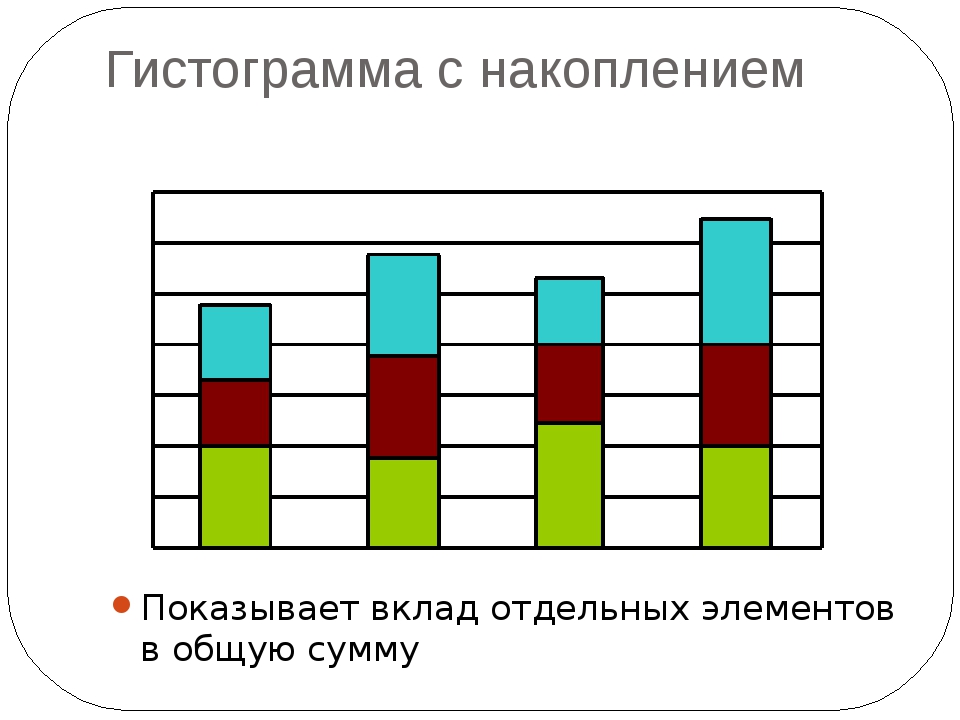

Вероятностные графики

Существует три типа категоризованных вероятностных графиков: нормальные, полунормальные и с исключенным трендом. Нормальные вероятностные графики — это быстрый способ визуальной проверки степени соответствия данных нормальному распределению.

В свою очередь категоризованные вероятностные графики дают возможность исследовать близость к нормальному распределению различных подгрупп данных .

Категоризованные нормальные вероятностные графики представляют собой эффективный инструмент для исследования однородности группы наблюдений с точки зрения соответствия нормальному распределению.

Графики квантиль-квантиль

Категоризованные графики квантиль-квантиль (или К-К) используются для поиска в определенном семействе распределений того распределения, которое наилучшим образом описывает имеющиеся данные.

В случае категоризованных графиков К-К строится набор графиков квантиль-квантиль, по одному для каждого значения категориальных переменных (X или X и Y) или для заданных условий выбора сложных подгрупп (см. Методы категоризации). Для графиков К-К используются следующие семейства распределений: экспоненциальное, экстремальное, нормальное, Релея, бета-, гамма-, логнормальное и Вейбулла.

Графики вероятность-вероятность

Категоризованные графики вероятность-вероятность (или В-В) используются для проверки соответствия конкретного теоретического распределения имеющимся исходным данным. На этих графиках для каждого значения категориальных переменных (X или X и Y) или для заданных условий выбора сложных подгрупп (см. Методы категоризации) создается по одному графику вероятность-вероятность.

На графиках В-В строится наблюдаемая функция распределения (доля непропущенных значений x) в зависимости от теоретической функции распределения, чтобы оценить соответствие этой теоретической функции наблюдаемым данным. Если все точки этого графика располагаются на диагонали (содержащей точку 0 и имеющей наклон 1), то можно заключить, что наблюдаемое распределение хорошо аппроксимируется данной теоретической функцией.

Если не все точки данных располагаются на диагональной линии, то на таком графике можно визуально выделить группы наблюдений, соответствующие и не соответствующие искомому распределению (если, к примеру, точки образуют кривую S-образной формы вокруг диагональной линии, то к ним можно применить определенное преобразование для приведения к нужной форме распределения).

Линейные графики

На линейных графиках отдельные точки данных соединяются линиями. Это простой способ визуального представления последовательности значений (например, цены на фондовом рынке за несколько дней торгов). Категоризованные линейные графики строятся в том случае, если необходимо разбить данные на несколько групп (категоризовать) с помощью группирующей переменной (например, цены при закрытии рынка по понедельникам, вторникам и т.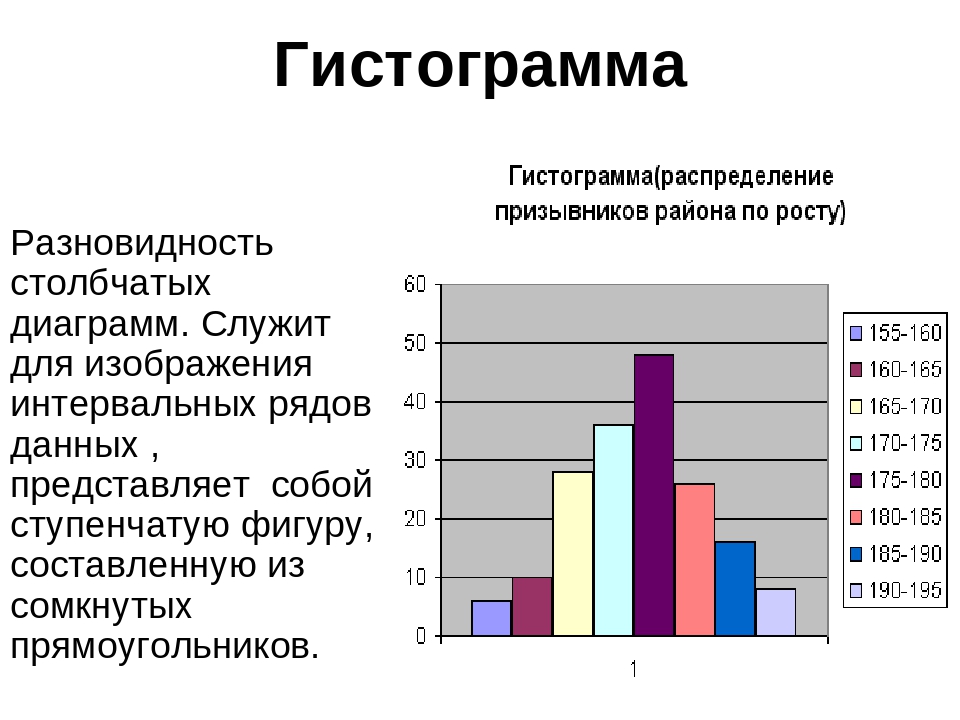 д.) или с помощью логических условий, составленных по нескольким переменным (например, цены при закрытии рынка в те дни, когда две другие акции и индекс Доу Джонса выросли по сравнению с другими ценами закрытия; см. Методы категоризации).

Диаграммы размаха

На диаграммах размаха (этот термин был впервые использован Тьюки в 1970 году) представлены диапазоны значений выбранной переменной (или переменных) для отдельных групп наблюдений. Для выделения этих групп используются от одной до трех категориальных (группирующих) переменных или набор логических условий выбора подгрупп.

Для каждой группы наблюдений вычисляется центральная тенденция (медиана или среднее), а также размах или изменчивость (квартили, стандартные ошибки или стандартные отклонения). Выбранные параметры отображаются на графике одним из пяти способов (Прямоугольники-Отрезки, Отрезки, Прямоугольники, Столбцы или Верхние-нижние засечки).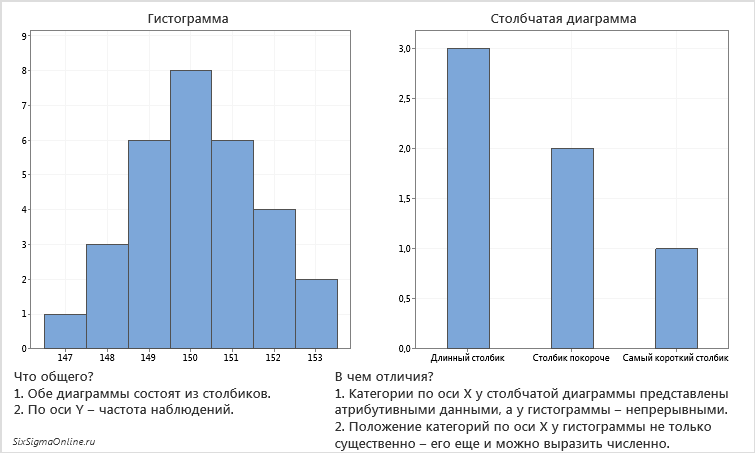 На этом графике можно показать и выбросы (см. разделы о выбросах и крайних точках).

На следующем графике, например, выбор факторов можно было бы считать вполне удачным, если бы не «досадное» несоответствие, на которое указывают выделенные на рисунке выбросы (в данном случае это значения, попадающие за пределы 1,5 квартильных размахов):

А на следующем рисунке не показаны ни выбросы, ни крайние точки.

Можно выделить два основных направления использования диаграмм размаха: (a) отображение диапазонов значений отдельных элементов, наблюдений или выборок (например, типичные минимаксные графики цен на акции или товары или графики агрегированных данных с диапазонами), (б) отображение изменения значений в отдельных группах или выборках (например, когда точкой внутри прямоугольника представлено среднее значение для каждой выборки, сам прямоугольник соответствует значениям стандартной ошибки, а меньший прямоугольник или пара «отрезков» обозначает стандартное отклонение от среднего).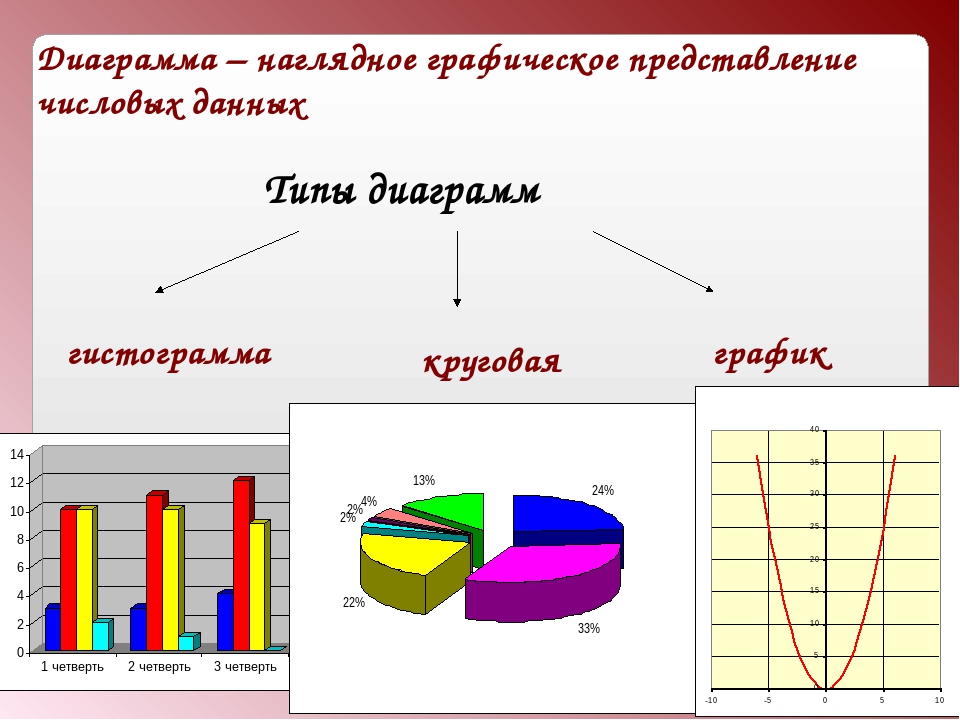

С помощью диаграмм размаха, на которых представлены характеристики изменчивости, можно быстро оценить и «интуитивно представить» силу связи между группирующей и зависимой переменной. Предположив, что зависимая переменная нормально распределена, и зная долю наблюдений, попадающих, к примеру, в интервал ±1 или ±2 стандартных отклонения от среднего (см. Элементарные понятия статистики), можно сделать, например, вывод о том, что 95% наблюдений из экспериментальной группы 1 попадают в другой диапазон значений, нежели 95% наблюдений из группы 2.

На этих графиках можно изобразить и так называемые усеченные средние (этот термин был впервые использован Тьюки в 1962 году), которые вычисляются после исключения заданного пользователем процента наблюдений с концов (хвостов) распределения.

Круговые диаграммы

Одним из наиболее широко используемых типов графического представления данных являются круговые диаграммы, на которых показаны пропорции или сами значения переменных. Категоризованные графики этого типа состоят из нескольких круговых диаграмм, где данные разделены по группам с помощью одной или нескольких группирующих переменных (например, gender) или категоризованы согласно логическим условиям выбора подгрупп (см. Методы категоризации).

В дальнейшем, говоря о категоризации этих графиков, мы будем иметь ввиду круговые диаграммы частот (в противоположность круговым диаграммам значений). Эти типы графиков, называемые также частотными круговыми диаграммами, представляют данные аналогично гистограммам. Все значения выбранной переменной категоризуются с помощью заданного метода категоризации, а затем относительные значения частот отображаются в виде сегментов круговой диаграммы пропорционального размера. Таким образом, эти графики являются альтернативным представлением гистограммы частот (см. раздел о категоризованных гистограммах).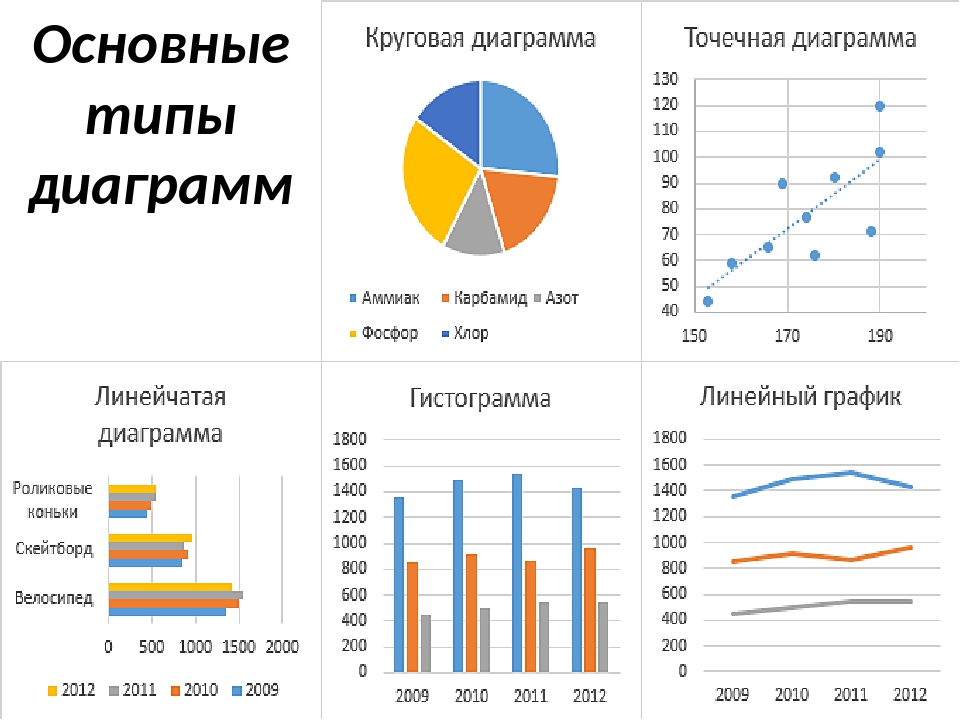

Диаграммы рассеяния круговых диаграмм. Еще одно очень полезное применение категоризованных круговых диаграмм — это представление относительных частот значений какой-либо переменной в различных «местах» совместного распределения двух других переменных. Например:

Обратите внимание, что круговые диаграммы изображены только в тех «местах», где имеются данные. Показанный выше график напоминает диаграмму рассеяния (переменных L1 и L2), где маркерами точек являются круговые диаграммы. Однако помимо обычной информации, содержащейся в диаграмме рассеяния, здесь в каждой точке дополнительно показано относительное распределение третьей переменной (а именно, доля значений Low, Medium и High Quality).

Графики пропущенных значений и данных вне диапазона

На этих графиках можно наглядно представить структуру распределения точек данных, содержащих пропущенные значения или находящихся «вне диапазонов», заданных пользователем. При этом строится по одной двумерной диаграмме для каждой группы наблюдений, выделенной с помощью группирующих переменных или с помощью условий выбора сложных подгрупп (см. Методы категоризации).

Эти типы графиков используются в разведочном анализе данных, чтобы определить, является ли случайным распределение точек с пропущенными значениями, а также для оценки их диапазона.

Трехмерные (3М) графики

Трехмерные диаграммы рассеяния (пространственные, спектральные, трассировочные и диаграммы отклонений), карты линий уровня и поверхности также можно построить для подгрупп наблюдений, заданных с помощью выбранной категориальной переменной или логических условий выбора (см. Методы категоризации). Основная задача этих графиков - упростить сравнение взаимосвязей между тремя и более переменными для различных групп или категорий наблюдений.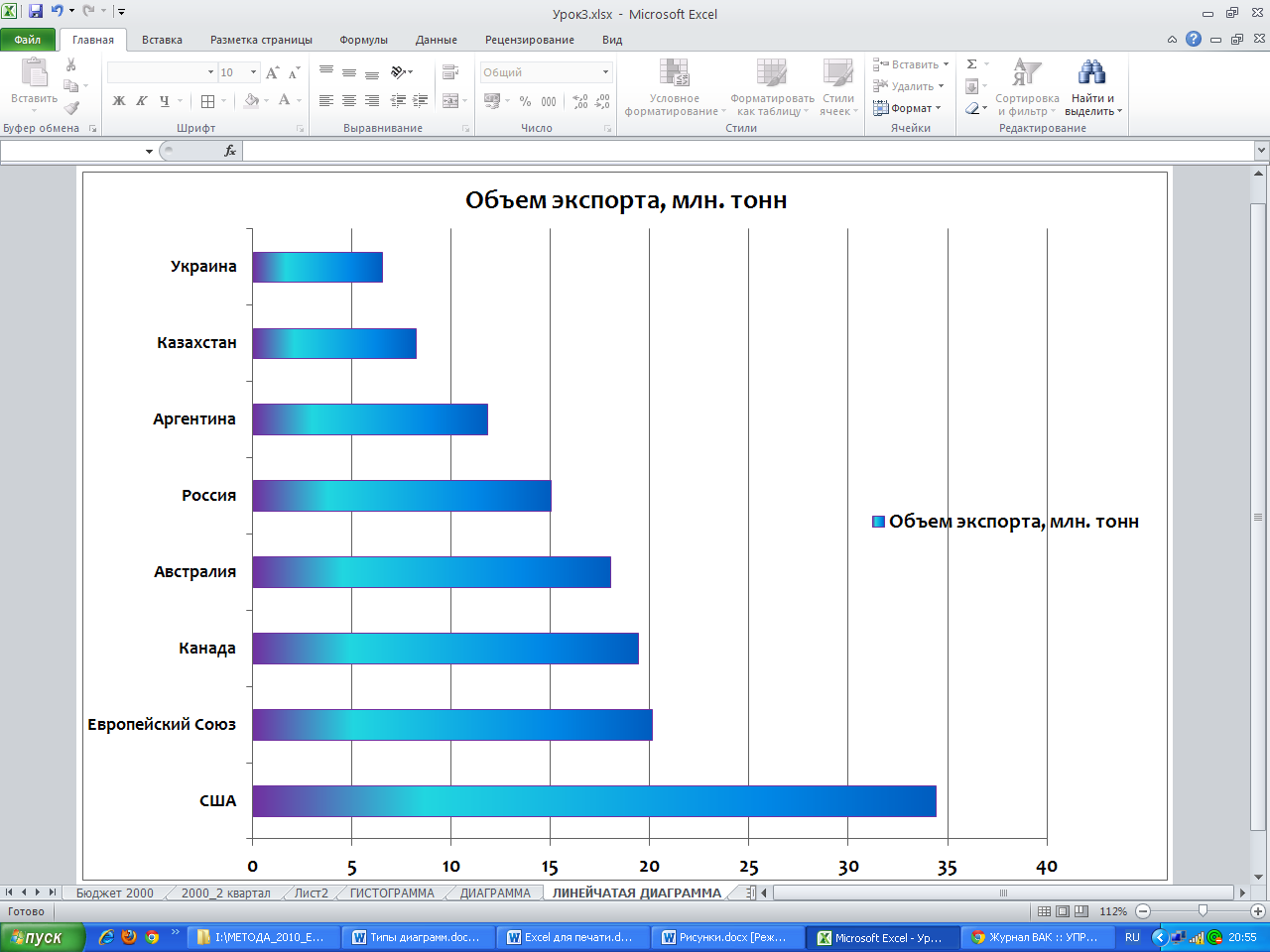

Применения. Трехмерные графики в координатах XYZ отображают взаимосвязи между тремя переменными. С помощью различных способов категоризации можно исследовать эти зависимости при различных условиях (т.е. в разных группах).

Изучая, например, показанный ниже категоризованный график поверхности, можно сделать вывод о том, что величина допуска прибора не влияет на измерения (переменные Depend1, Depend2 и Height), кроме случая, когда она 3.

Этот вывод становится еще более очевидным, если использовать вместо поверхности карту линий уровня.

Тернарные графики

Категоризованные тернарные графики используются для исследования взаимосвязей между тремя и более переменными, три из которых представляют собой компоненты смеси (т.е. для каждого наблюдения значения их суммы являются постоянной величиной), при этом отдельный график строится для каждого уровня группирующей переменной.

Для построения тернарных графиков используется треугольная система координат на плоскости или в пространстве и строится зависимость между четырьмя (или более) переменными (компонентами X, Y и Z и откликами V1, V2 и т.д.). При этом накладываются ограничения на относительные значения каждой из компонент, чтобы они в сумме давали одинаковую величину для каждого наблюдения (например, 1).

На категоризованных тернарных графиках строится по одному графику для каждого значения группирующей переменной (или заданного пользователем подмножества данных), и все они отображаются в одном графическом окне, чтобы можно было сравнивать различные подгруппы наблюдений.

Применения. Эти графики применяются для анализа результатов эксперимента, в котором измеряемый отклик зависит от относительного соотношения трех компонент (например, трех химических веществ при составлении смесей), которое варьируется с целью определения его оптимального значения.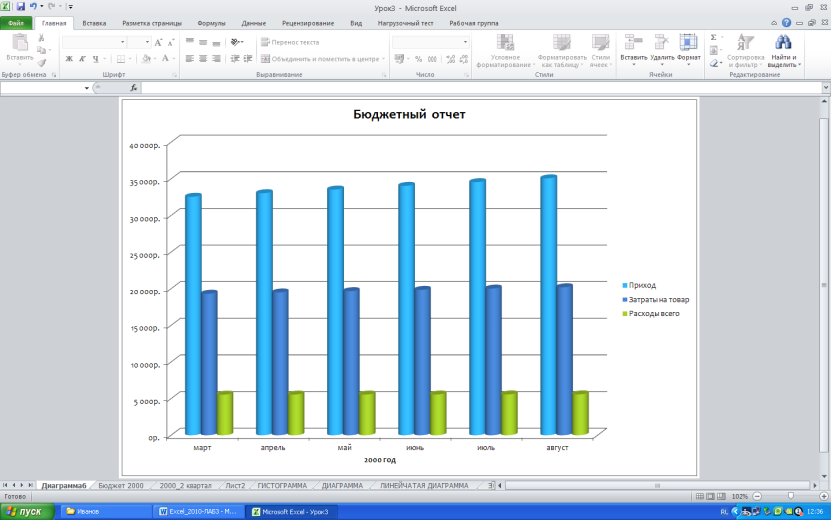 Эти типы графического представления можно использовать и в других случаях, когда взаимосвязь между переменными, на которые наложены определенные ограничения, необходимо исследовать для различных групп или категорий наблюдений.

Закрашивание

Закрашивание является одним из первых и, по-видимому, наиболее широко распространенных методов, известных как графический разведочный анализ данных. Этот метод позволяет интерактивно выделять на экране отдельные точки или подмножества данных и задавать их характеристики, или исследовать их влияние на взаимосвязи между переменными (например, на матрицах диаграмм рассеяния) и идентифицировать выбросы(например, с помощью меток).

Связи между переменными можно наглядно представить с помощью аппроксимирующих функций (например, двумерных кривых или трехмерных поверхностей) и доверительных интервалов.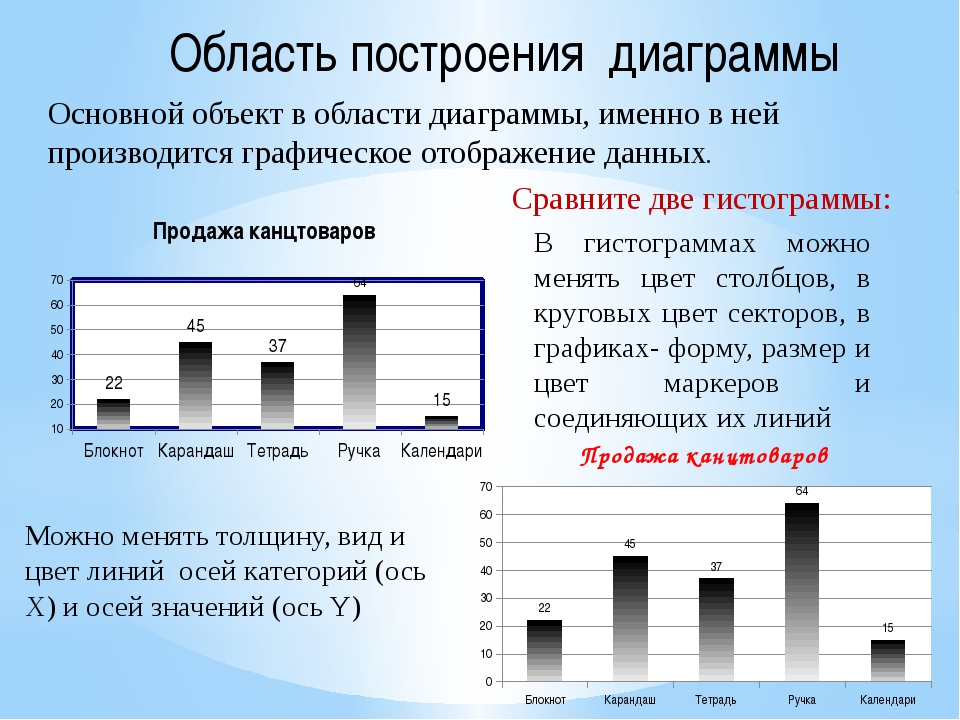 Интерактивно удаляя или добавляя определенные подгруппы наблюдений, можно наблюдать за изменениями этих функций и их параметров. Одно из применений метода закрашивания — это, например, выделение на матричной диаграмме рассеяния всех точек данных, принадлежащих определенной категории (например, на показанном ниже рисунке на правом верхнем графике выделена группа наблюдений, соответствующих значению «среднего» уровня дохода).

Такое исследование помогает определить, как эти конкретные наблюдения влияют на связи между другими переменными того же набора данных (например, на корреляцию между «расходами» и «активами»).

В режиме «динамического закрашивания» (см. следующий пример) или «автоматического обновления функции подгонки» можно задать движение кисти по определенным последовательным диапазонам выбранной переменной (например, непрерывной, а не дискретной, как на показанном ранее примере) и исследовать динамику вклада этой переменной в связи между другими переменными этого набора данных.

Сглаживание двумерных распределений

Для наглядного представления таблицы значений двух переменных используются трехмерные гистограммы. Их можно рассматривать как объединение двух простых гистограмм для совместного анализа частот значений двух переменных. Чаще всего на этом графике для каждой «ячейки» таблицы нарисован один трехмерный столбец, а его высота соответствует частоте значений в этой ячейке. При построении трехмерной гистограммы для каждой из двух переменных можно использовать свой метод категоризации (см. ниже).

Когда предусмотрены процедуры сглаживания данных, то трехмерное представление частот значений можно аппроксимировать поверхностью. Такое сглаживание можно осуществить для любой трехмерной гистограммы. Для достаточно простой структуры данных (как на предыдущем рисунке) такое сглаживание не имеет особого смысла.

Однако, в случае более сложной картины распределения частот эта процедура может оказаться эффективным инструментом разведочного анализа данных

и позволит выявить особенности, которые трудно обнаружить на обычной трехмерной гистограмме (например, показанную выше «волновую структуру» поверхности).

Послойное сжатие

На графиках этого типа за счет сокращения области основного графика освобождается место для графиков на полях, которые располагаются в правой и верхней части графического окна (включая маленький угловой график). Эти графики на полях представляют собой соответственно вертикально и горизонтально сжатые изображения основного графика.

Послойное сжатие двумерных графиков является методом разведочного анализа данных, который дает возможность скрытые тренды и структуры двумерных наборов данных. Рассмотрим следующий рисунок.

Здесь на примере, приведенном Кливландом (Cleveland, 1993), можно убедиться, что в каждом цикле солнечной активности число пятен уменьшается гораздо медленнее, чем нарастает в начале цикла. Такое поведение совершенно не очевидно при исследовании обычного линейного графика, в то время как сжатый график позволяет обнаружить эту скрытую картину.

Проекции трехмерных наборов данных

Полезным методом изучения и аналитического исследования структуры поверхности (созданной, как правило, по трехмерным наборам данных) является построение ее проекции на плоскость в виде карты линий уровня.

Эти графики менее эффективны для быстрого визуального анализа формы трехмерных структур по сравнению с графиками поверхности,

однако их преимущество заключается в возможности точного исследования формы поверхности —

на картах линий уровня отображается ряд не искаженных горизонтальных «сечений».

Пиктографики

На пиктографиках каждое наблюдение представлено в виде многомерного символа, что позволяет использовать эти типы графического представления данных в качестве не очень простого, но мощного исследовательского инструмента. Главная идея такого метода анализа основана на человеческой способности «автоматически» фиксировать сложные связи между многими переменными, если они проявляются в последовательности элементов (в данном случае «пиктограмм»). Иногда понимание (или «чувство») того, что некоторые элементы «чем-то похожи» друг на друга, приходит раньше, чем наблюдатель (аналитик) может объяснить, какие именно переменные обусловливают это сходство (Lewicki, Hill, & Czyzewska, 1992). Конкретную природу проявившихся взаимосвязей между переменными позволяет выявить уже последующий анализ данных, основанный на изучении этого интуитивно обнаруженного сходства.

Основная идея пиктографиков заключается в представлении элементарных наблюдений как отдельных графических объектов, где значения переменных соответствуют определенным чертам или размерам объекта (обычно одно наблюдение = одному объекту). Это соответствие устанавливается таким образом, чтобы общий вид объекта менялся в зависимости от конфигурации значений.

Таким образом, объекты имеют определенный «внешний вид», который уникален для каждой конфигурации значений и может быть идентифицирован наблюдателем. Изучение таких пиктограмм помогает выявить как простые связи, так и сложные взаимодействия между переменными.

Анализ пиктографиков

Целесообразно проводить анализ пиктографиков в пять этапов.
Сначала выберите порядок анализируемых переменных. В большинстве случаев наилучшим вариантом оказывается случайная последовательность. Кроме того, можно попробовать расположить их в порядке, соответствующем полученному уравнению множественной регрессии, факторным нагрузкам или объясняемым факторам (см. главу Факторный анализ). Таким образом можно упростить и сделать более «однородным» общий вид пиктограмм, чтобы легче идентифицировать слабо выраженные различия. В то же время такой подход может затруднить идентификацию некоторых структур. На этом этапе можно дать только один универсальный совет: прежде чем использовать какие-либо сложные методы, попробуйте наиболее простой и быстрый вариант, а именно, случайную последовательность переменных.

Попробуйте обнаружить какие-либо закономерности, например, сходства между группами пиктограмм, выбросы или определенные связи между элементами (например, » если первые два луча звезды длинные, то как правило, с другой стороны есть один или два коротких луча»). На этом этапе лучше использовать пиктографики кругового типа.

При обнаружении закономерностей постарайтесь сформулировать их в терминах конкретных переменных.

Измените соответствие переменных и элементов пиктограмм (или переключитесь на один из последовательных пиктографиков), чтобы проверить обнаруженную структуру взаимосвязей (например, попробуйте переместить ближе друг к другу элементы, между которыми обнаружена связь). В некоторых случаях в конце этого этапа целесообразно исключить из рассмотрения те переменные, которые не вносят явного вклада в обнаруженную структуру.

И наконец, используйте один из численных методов (таких как регрессионный анализ, нелинейное оценивание, дискриминантный или кластерный анализ), чтобы проверить и попытаться количественно оценить обнаруженные закономерности или хотя бы их часть.

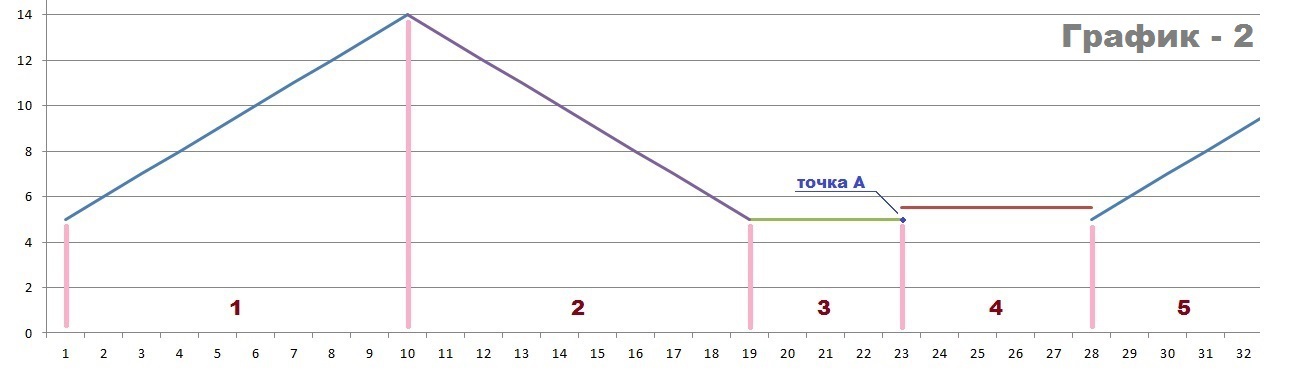
Систематизация пиктографиков

Большинство пиктографиков можно отнести к одной из двух групп: круговые и последовательные.

Круговые пиктографики. Круговые пиктографики (звезды, лучи, многоугольники) имеют вид «велосипедного колеса», на них значения переменных представлены расстояниями между центром пиктограммы («втулкой») и их концами.

Такие графики могут помочь в обнаружении связей между переменными, которые проявляются в общей структуре пиктограмм и зависят от конфигурации значений самих переменных.

Чтобы описать такую » общую картину» в терминах конкретных моделей или проверить имеющиеся предположения, имеет смысл использовать последовательные пиктографики, которые могут оказаться более эффективными, если уже известно, что именно требуется обнаружить.

Последовательные пиктографики. Последовательные пиктографики (столбцы, профили, линии) представляют собой набор картинок с маленькими последовательными графиками (различных типов).

Значения переменных представлены здесь расстояниями между основанием пиктограммы и последовательными точками (например, высотами показанных выше столбцов). Эти графики менее эффективны на начальной стадии разведочного анализа, поскольку пиктограммы очень похожи между собой. Однако, как уже упоминалось ранее, такое представление может быть весьма полезным для проверки уже сформулированной гипотезы.

Пиктограммы круговых диаграмм. Эти пиктографики нельзя однозначно отнести к одной из двух групп. Все они имеют круговую форму, но в то же время последовательно разделены в соответствии с значениями переменных.

Их можно отнести скорее к последовательным, чем к круговым пиктографикам, но можно использовать и в том, и в другом случае.

«Лица Чернова». Этот тип пиктографиков составляет отдельную группу. Здесь каждое наблюдение представляет собой схематичное изображение лица, определенным чертам которого соответствуют относительные значения выбранных переменных.

Некоторые исследователи рассматривают этот способ графического представления данных как уникальный многомерный метод разведочного анализа, позволяющий выявить такие скрытые картины взаимосвязей между переменными, которые не могут быть обнаружены другими методами. Вероятно, такое заявление можно считать преувеличением. Кроме того, следует заметить, что этот способ исследования весьма непрост в применении и требует большого опыта в том, что касается сопоставления переменных чертам лица. См. также раздел Методы «добычи данных» .

Стандартизация значений

Как правило, при построении пиктографиков значения переменных должны быть стандартизованы, чтобы их можно было сравнивать в пределах одной пиктограммы. Исключения составляют те случаи, когда на пиктограммах необходимо отобразить глобальные различия диапазонов выбранных переменных. Поскольку масштаб пиктограммы определяется наибольшим значением, то на пиктограмме могут отсутствовать те переменные, которые имеют значения другого порядка малости, например, на пиктограмме звезды некоторые лучи могут оказаться настолько короткими, что совсем не будут видны..

Применения

Пиктографики обычно используются: (1) для обнаружения структур или кластеров наблюдений и (2) для исследования сложных взаимосвязей между несколькими переменными. Первый вариант соответствует кластерному анализу; т.е. процедуре классификации наблюдений.

Предположим, вы изучали характеры актеров и записали их ответы на вопросы анкеты. С помощью пиктографика можно определить, существуют ли группы артистов, которые отличаются по их ответам на заданные вопросы (можно, к примеру, обнаружить, что некоторые артисты являются творческими, недисциплинированными и независимыми личностями, в то время как другая группа состоит из умных, дисциплинированных людей, которые ценят свою популярность).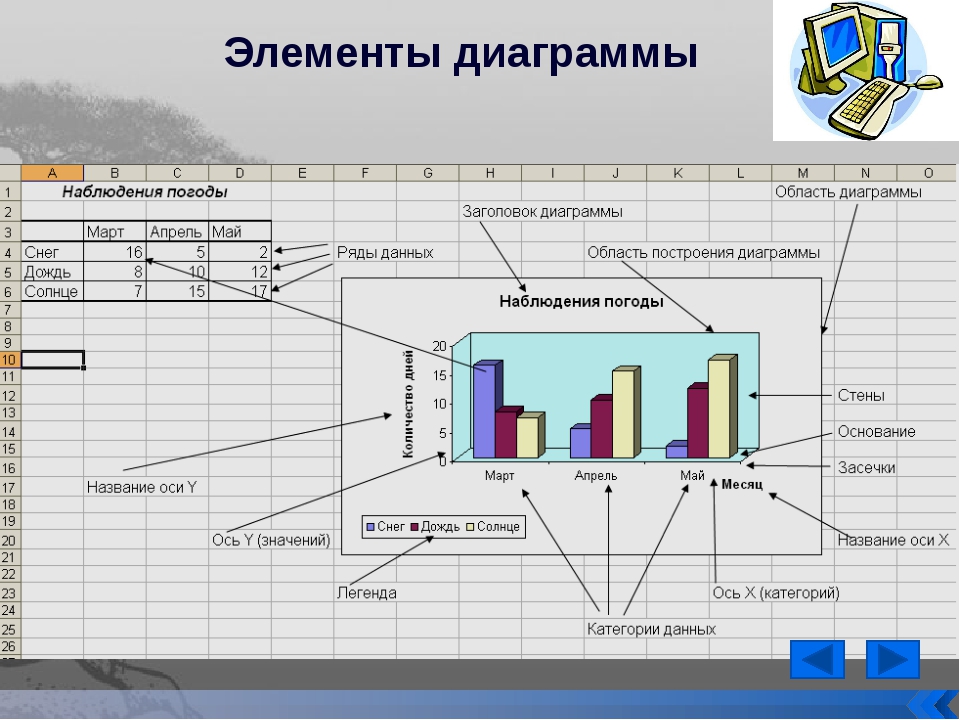

Другая область применений — изучение взаимосвязей между переменными — напоминает факторный анализ, который используется для исследования вопроса о зависимости переменных. Предположим, изучалось мнение группы людей о различных марках автомобилей. В файле данных записаны средние оценки по каждому из свойств (рассматриваемых как переменные) для каждого из автомобилей (рассматриваемых как наблюдения).

При изучении «лиц Чернова» (где каждое лицо представляет мнение об одном из автомобилей) может оказаться, что улыбающиеся лица обычно имеют большие уши; при этом, если цене соответствует «ширина» улыбки, а динамическим качествам — размер ушей, то это «открытие» означает, что быстрые машины являются более дорогими. Разумеется, это очень простой пример; однако при реальном анализе данных применение этого метода может сделать более очевидными сложные взаимосвязи между многими переменными.

Близкие способы графического представления

Связи между переменными из одного или двух списков могут быть представлены на матричных графиках. Использование матричных графиков одновременно с выделением подгрупп позволяет получить информацию, подобную той, которая отображается на пиктографиках.

Если использовать методы выделения подгрупп на диаграммах рассеяния, то для исследования взаимосвязей между двумя переменными можно использовать обычные 2М диаграммы рассеяния; а в случае трех переменных — 3Мдиаграммы рассеяния.

Типы графиков

Существуют различные типы пиктографиков.

«Лица Чернова». Для каждого наблюдения рисуется отдельное «лицо»; при этом относительные значения выбранных переменных соответствуют форме и размерам определенных его черт (например, длине носа, изгибу бровей, ширине лица).

Дополнительно см. абзац «Лица Чернова» в разделе Систематизация пиктографиков.

Звезды. Это пиктографики кругового типа. Для каждого наблюдения рисуется пиктограмма в виде звезды; относительные значения выбранных переменных соответствуют относительным длинам лучей каждой звезды (по часовой стрелке, начиная с 12:00). Концы лучей соединены линиями.

Лучи. Эти пиктографики также относятся к круговому типу. Для каждого наблюдения строится одна пиктограмма. Каждый луч соответствует одной из выбранных переменных (по часовой стрелке, начиная с 12:00), и на нем отложено значение соответствующей переменной. Эти значения соединены линиями.

Многоугольники. Это пиктографикикругового типа. Для каждого наблюдения рисуется отдельный многоугольник; относительные значения выбранных переменных соответствуют расстояниям вершин от центра многоугольника (по часовой стрелке, начиная с 12:00).

Круговые диаграммы. Это пиктографики кругового типа. Для каждого наблюдения рисуется круговая диаграмма; относительные значения выбранных переменных соответствуют размерам сегментов диаграммы (по часовой стрелке, начиная с 12:00).

Столбцы. Это пиктографики последовательного типа. Для каждого наблюдения строится столбчатая диаграмма; относительные значения выбранных переменных соответствуют высотам последовательных столбцов.

Линии. Это пиктографики последовательного типа.

Для каждого наблюдения строится линейный график; относительные значения выбранных переменных соответствуют расстояниям точек излома линии от основания графика.

Профили. Это пиктографики последовательного типа. Для каждого наблюдения строится зонный график; относительные значения выбранных переменных соответствуют расстояниям последовательных пиков сечения над линией основания.

Маркировка пиктограмм

Если программа позволяет вам выделять подгруппы наблюдений, то это свойство можно использовать и для маркировки соответствующих пиктограмм. При этом вокруг выделенных пиктограмм будут нарисованы рамки.

Шаблоны рамок, идентифицирующих заданные подгруппы, будут показаны в условных обозначениях рядом с текстом соответствующих условий выбора наблюдений. На следующем графике показан пример маркированных подгрупп.

Все наблюдения, удовлетворяющие условию для подгруппы 1 (значение переменной Iristype равно значению переменной Setosa и номер наблюдения меньше 100), обозначены специальной рамкой вокруг пиктограммы.

А все наблюдения, которые удовлетворяют условию для подгруппы 2 (значение переменной Iristype равно значению переменной Virginic и номер наблюдения меньше 100), обозначены на графике рамкой другого цвета.

Выборка данных

Иногда отображение на графике слишком большого числа точек данных затрудняет изучение их структуры (см. следующий рисунок). Если файл данных слишком большой, то имеет смысл показать на графике лишь подмножество наблюдений, чтобы общая картина не была скрыта маркерами точек.

Некоторые программы предлагают методы выборки (или оптимизации) данных, которые в ряде случаев могут оказаться весьма полезны. При этом пользователь может задать целое число n, меньшее числа наблюдений в файле данных, а программа случайным образом выберет из этого файла приблизительно n допустимых наблюдений и именно их построит на графике.

Заметим, что такие методы сокращения набора данных (или размера выборки) эффективно отображают случайную структуру этих данных. Очевидно, эти методы принципиально отличаются от методов выделения конкретного подмножества или подгруппы наблюдений с помощью определенных критериев (например, по полу, области или уровню холестерина). Последние можно применять интерактивно (например, в режиме динамического закрашивания) или каким-либо другим способом (например, на категоризованных графиках или с помощью условий выбора наблюдений). Все эти методы в равной мере могут помочь в идентификации сложной структуры большого набора данных.

Вращение (в трехмерном пространстве)

Изменение угла зрения при отображении трехмерной диаграммы рассеяния (простой, спектральной или пространственной) может оказаться эффективным средством для выявления некоторой структуры, которая видна только при определенном повороте «облака» точек (см. следующий рисунок).

Некоторые программы предоставляют полезный инструмент для интерактивного изменения перспективы и вращения изображения. Эти средства контроля изображения позволяют подобрать подходящий угол зрения и перспективу, чтобы найти наиболее удачное расположение «точки зрения» на график, а также дают возможность управлять его вращением в горизонтальной и вертикальной плоскости.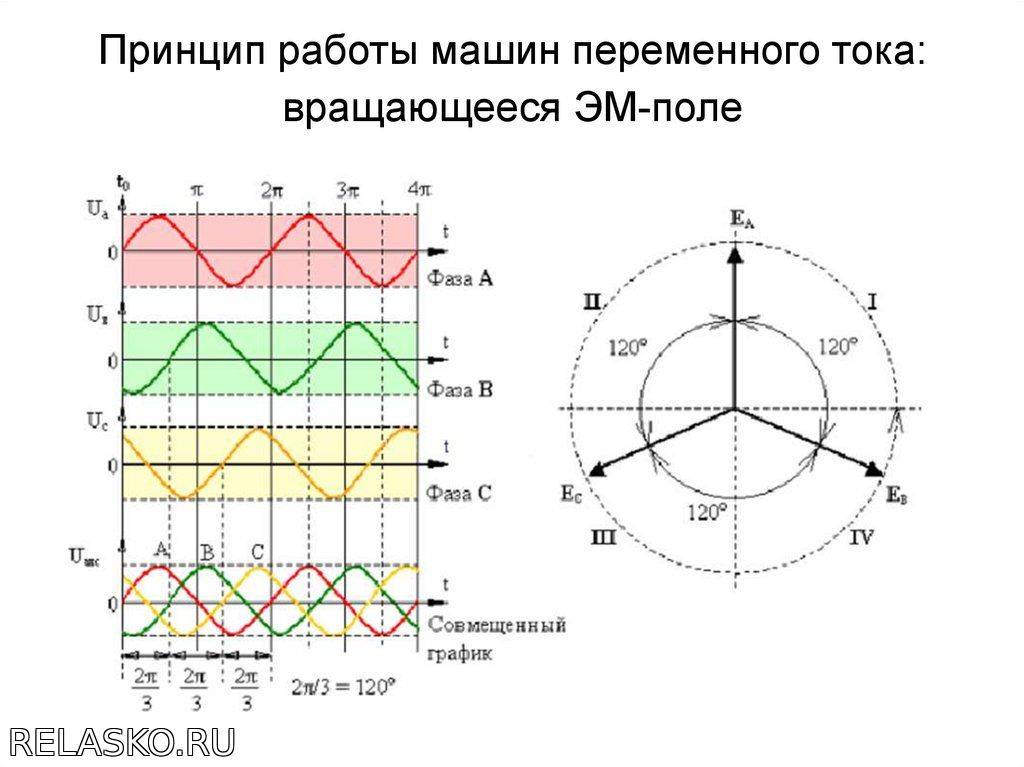

Эти инструменты могут оказаться весьма полезными не только при начальном разведочном анализе данных, но и при исследовании факторного пространства (см.Факторный анализ) или пространства размерностей (см. Многомерное шкалирование).

Все права на материалы электронного учебника принадлежат компании StatSoft

Разница между таблицей и графиком
Основное различие: таблицы представляют факты и цифры в виде строк и столбцов. Диаграммы представляют данные в более графической форме, которая может включать в себя линии, столбцы и круги.
Таблицы и диаграммы используются для представления данных. Однако манера и обстоятельства, в которых каждый из них используется, отличает их друг от друга. Таблицы представляют факты и цифры в формате строк и столбцов, что облегчает и ускоряет чтение и сравнение данных. С другой стороны, диаграммы представляют данные в более графической форме, которая может включать в себя линии, столбцы и круги. Таблицы довольно просты в использовании, в некоторых случаях они состоят только из нескольких столбцов и строк или упорядоченных иерархий, например, в таблице умножения. Это облегчает нам понимание, а не читает данные в длинных предложениях. Преимущество таблиц в том, что они взаимодействуют с нашей вербальной системой, что позволяет нам последовательно обрабатывать информацию. Мы читаем данные вниз по столбцам или по рядам чисел. Это облегчает сравнение данных рядом. Следовательно, нам будет легче понять и сделать выводы. Диаграммы, с другой стороны, используются для определения взаимосвязи между большим количеством данных и их частями. Они взаимодействуют с наша визуальная система и облегчить нам чтение и понимание данных. Они дают форму и форму данным. Затем наша визуальная система воспринимает формы и формы и расшифровывает их для извлечения шаблонов и связей между данными. Считается, что одна диаграмма может передавать важные характеристики данных более наглядно и запоминающе, чем столбцы данных. Графики обычно не содержат длинных текстов. В то же время над диаграммой появляется только текст, описывающий данные, на которые ссылаются в диаграмме. Данные на графическом графике обычно отображаются в виде сетки, состоящей из горизонтальной оси X или вертикальной оси Y. Если данные имеют несколько переменных, на диаграмме может быть легенда, в которой перечислены переменные на диаграмме для удобства идентификации. Таблица сравнения таблиц и диаграмм:
Таблица Диаграмма
Представление данных Числа и текст в строках и столбцах Графическое представление, включая линии, полосы и круги.
Характеристики Текст, цифры, легче сравнивать данные, представляет периодическую и изменчивую информацию, простую для понимания большое разнообразие, графика, мало текста, картинки, легче для понимания, визуальный характер
Когда использовать Чтобы найти или сравнить отдельные значения, чтобы показать точные значения, когда задействованы несколько единиц измерения. Чтобы передать сообщение, которое содержится в форме данных, выявить взаимосвязь между многими значениями.
Типы Простой стол, многомерный стол, широкие и узкие столы Гистограмма, линейчатая диаграмма, линейная диаграмма, круговая диаграмма, временная диаграмма, организационная диаграмма, древовидная диаграмма, блок-схема, картограмма (карта), родословная диаграмма (семейное древо), пузырьковая диаграмма, потоковая диаграмма, диаграмма каги, диаграмма рассеяния и т. Д.
Используется в Издательство, Математика, Естественные науки, Информационные технологии — разработка приложений и программного обеспечения. Математика, Естественные науки, Информационные технологии
Глава 6 Продвинутая графика | Визуализация и анализ географических данных на языке R
Предварительные требования
Для работы по теме текущей лекции вам понадобятся пакеты ggplot2, dplyr и tidyr из tidyverse. Помимо этого, мы будем работать напрямую с данными Евростата, NASA POWER и USDA NRCS Soil Data Access к которым можно обращаться напрямую с использованием пакетов eurostat, nasapower и soildb:
Пакет soilDB лучше устанавливать из консоли командой install.packages('soilDB', dependencies = TRUE). Указание параметра dependencies = TRUE обеспечит установку других пакетов, от которых он зависит.
В настоящей главе мы кратко познакомимся с системой ggplot2. gg расшифровывается как grammar of graphics. Под этим понимается определенная (какая — мы узнаем далее) система правил, позволяющих описывать и строить графики. ggplot довольно сильно отличается от стандартной графической подсистемы R. Прежде всего — модульным подходом к построению изображений. В ggplot вы собираете графики «по кирпичикам», отдельно определяя источник данных, способы изображения, параметры системы координат и т. д. – путем вызова и сложения результатов соответствующих функций.
При построении элементарных графиков ggplot может показаться (и по факту так и есть) сложнее, чем стандартная графическая подсистема. Однако при усложнении требований к внешнему виду и информационному насыщению графика сложность ggplot оказывается преимуществом, и с ее помощью относительно просто можно получать элегантные и информативные визуализации, на создание которых с помощью стандартной подсистемы пришлось бы затратить невероятные усилия! В этой главе мы кратко познакомимся с ggplot, а далее на протяжении курса будем регулярно ее использовать, осваивая новые возможности.
Загрузка данных Евростата
Таблицы данных Евростата имеют уникальные коды, по которым их можно загружать, используя API (Application programming interface). В этой лекции мы будем работать с данными о крупнейших международных партнерах Евросоюза по импорту и экспорту основных видов товаров. Например, таблица данных по продуктам питания, напиткам и табаку имеет код tet00034:
Для чтения таблиц по кодам в пакете eurostat имеется функция get_eurostat(). Чтобы год измерения получить в виде числа, а не объекта типа Date, используем второй параметр time_format = num. Для перехода от кодов продукции и стран к их полным наименованиям, дополнительно вызовем функцию label_eurostat() из того же пакета:
tables = c('tet00034', 'tet00033', 'tet00032', 'tet00031','tet00030', 'tet00029') trades = lapply(tables, function(X) { # прочтем несколько таблиц в список get_eurostat(X) |> label_eurostat() }) |> bind_rows() |> # объединим прочитанные таблицы в одну select(-geo) |> # убираем столбец с территорией торговли, т.к. там только Евросоюз dplyr::filter(stringr::str_detect(indic_et, 'Exports in|Imports in')) |> # оставим только экспорт и импорт pivot_wider(names_from = indic_et, values_from = values) |> # вынесем данные по экспорту и импорту в отдельные переменные rename(export = `Exports in million of ECU/EURO`, # дадим им краткие названия import = `Imports in million of ECU/EURO`) |> mutate(partner = as. factor(partner)) trades # посмотрим, что получилось ## # A tibble: 720 × 5 ## sitc06 partner time export import ## <chr> <fct> <date> <dbl> <dbl> ## 1 Food, drinks and tobacco Argentina 2008-01-01 81.3 7334 ## 2 Food, drinks and tobacco Brazil 2008-01-01 600. 9639. ## 3 Food, drinks and tobacco Canada 2008-01-01 1950. 1458. ## 4 Food, drinks and tobacco Switzerland 2008-01-01 5000. 2727. ## 5 Food, drinks and tobacco China except Hong Kong 2008-01-01 1322. 3567. ## 6 Food, drinks and tobacco Japan 2008-01-01 3964. 119. ## 7 Food, drinks and tobacco Norway 2008-01-01 2416. 3012. ## 8 Food, drinks and tobacco Russia 2008-01-01 7567. 855. ## 9 Food, drinks and tobacco Turkey 2008-01-01 1175 3160. ## 10 Food, drinks and tobacco United States 2008-01-01 10021.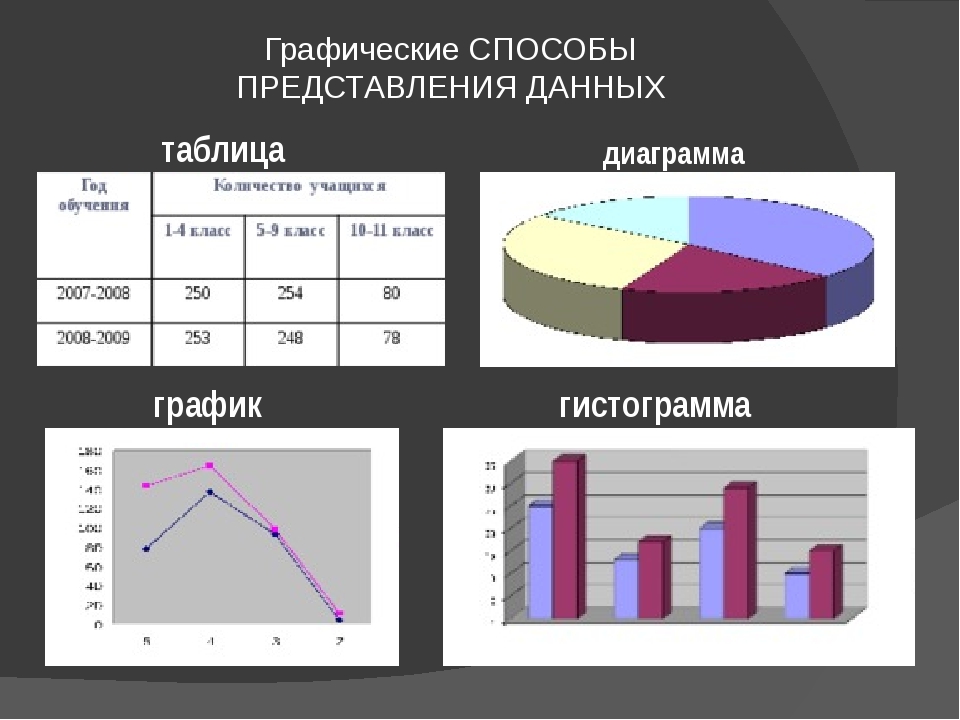 2/день\)) для той же точки с 1995 по 2015 год: interannual_sse <- get_power( community = "sse", lonlat = c(60.59, 56.84), dates = 1995:2015, temporal_api = "interannual", pars = c("CLRSKY_SFC_SW_DWN", "ALLSKY_SFC_SW_DWN") ) interannual_sse # посмотрим, что получилось Загрузка данных Soil Data Access Soil Data Access — это онлайн-сервис департамента сельского хозяйства США, который позволяет получать подробные данные о почвенных ресурсах этой страны. Наиболее часто запрашиваются данные по так называемым почвенным сериям — группам почвенных профилей, обладающих схожими характеристиками и, таким образом, идентичными с точки зрения сельскохозяйственного использования. Как правило, серии именуются по названию населенного пункта, рядом с которым впервые были найдены подобные почвы. Например, серия Cecil имеет следующее покрытие и обеспеченность разрезами в базе данных SDA при запросе на сайте Series Extent Explorer: Для запросов данных по почвенным сериям достаточно вызвать функцию fetchOSD и передать ей имя одной или более серий: soils = c('wilkes', 'chewacla', 'congaree') series = fetchOSD(soils, extended = TRUE) Результирющий объект представляет собой список со множеством таблиц, которые характеризуют как почвенную серию в целом, так и отдельные ее разрезы: str(series) ## List of 14 ## $ SPC :Formal class 'SoilProfileCollection' [package "aqp"] with 9 slots ## . . ..@ idcol : chr "id" ## .. ..@ hzidcol : chr "hzID" ## .. ..@ depthcols : chr [1:2] "top" "bottom" ## .. ..@ metadata :List of 8 ## .. .. ..$ aqp_df_class : chr "data.frame" ## .. .. ..$ aqp_group_by : chr "" ## .. .. ..$ aqp_hzdesgn : chr "hzname" ## .. .. ..$ aqp_hztexcl : chr "texture_class" ## .. .. ..$ depth_units : chr "cm" ## .. .. ..$ stringsAsFactors: logi FALSE ## .. .. ..$ original.order : int [1:22] 1 2 3 4 5 6 7 8 9 10 ... ## .. .. ..$ origin : chr "OSD via Soilweb / fetchOSD" ## .. ..@ horizons :'data.frame': 22 obs. of 21 variables: ## .. .. ..$ id : chr [1:22] "CHEWACLA" "CHEWACLA" "CHEWACLA" "CHEWACLA" ... ## .. .. ..$ top : int [1:22] 0 10 36 66 97 119 152 0 20 46 ... ## .. .. ..$ bottom : int [1:22] 10 36 66 97 119 152 203 20 46 56 ... ## .. .. ..$ hzname : chr [1:22] "Ap" "Bw1" "Bw2" "Bw3" ... ## .. .. ..$ soil_color : chr [1:22] "#7E5A3BFF" "#7A5C37FF" "#7A5C37FF" "#7E5A3BFF" . .. ## .. .. ..$ hue : chr [1:22] "7.5YR" "10YR" "10YR" "7.5YR" ... ## .. .. ..$ value : int [1:22] 4 4 4 4 5 5 4 4 4 3 ... ## .. .. ..$ chroma : int [1:22] 4 4 4 4 8 1 4 4 3 3 ... ## .. .. ..$ dry_hue : chr [1:22] "7.5YR" "10YR" "10YR" "7.5YR" ... ## .. .. ..$ dry_value : int [1:22] 6 6 6 6 6 6 6 6 6 5 ... ## .. .. ..$ dry_chroma : int [1:22] 4 4 4 4 7 1 4 4 3 3 ... ## .. .. ..$ texture_class : Ord.factor w/ 21 levels "coarse sand"<..: 13 18 17 13 17 17 13 13 13 NA ... ## .. .. ..$ cf_class : logi [1:22] NA NA NA NA NA NA ... ## .. .. ..$ pH : logi [1:22] NA NA NA NA NA NA ... ## .. .. ..$ pH_class : Ord.factor w/ 12 levels "ultra acid"<"extremely acid"<..: 3 3 3 3 3 3 3 4 NA NA ... ## .. .. ..$ distinctness : chr [1:22] "clear" "gradual" "gradual" "gradual" ... ## .. .. ..$ topography : chr [1:22] "smooth" "wavy" "wavy" "wavy" .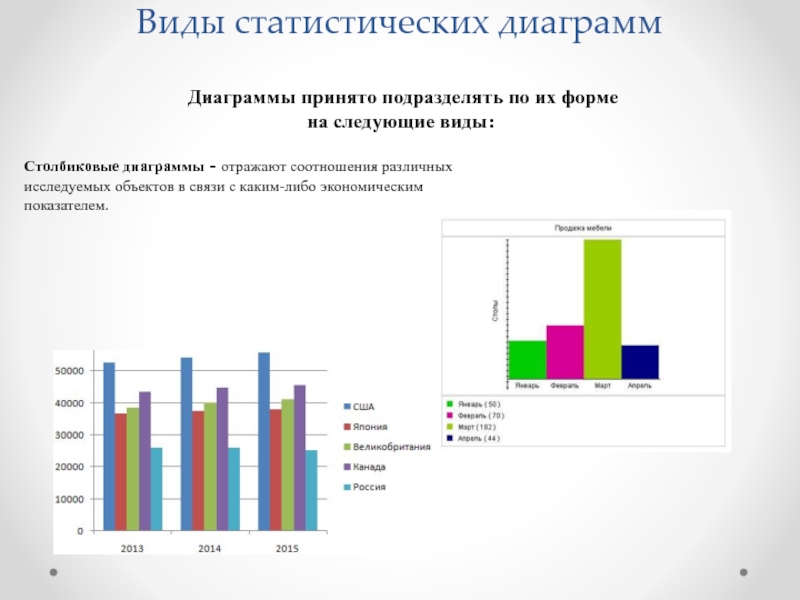 .. ## .. .. ..$ dry_color_estimated : logi [1:22] TRUE TRUE TRUE TRUE TRUE TRUE ... ## .. .. ..$ moist_color_estimated: logi [1:22] FALSE FALSE FALSE FALSE FALSE FALSE ... ## .. .. ..$ narrative : chr [1:22] "Ap--0 to 4 inches; brown (7.5YR 4/4) loam; weak medium granular structure; friable; common very fine, fine, and"| __truncated__ "Bw1--4 to 14 inches; dark yellowish brown (10YR 4/4) silty clay loam; weak medium subangular blocky structure; "| __truncated__ "Bw2--14 to 26 inches; dark yellowish brown (10YR 4/4) clay loam; weak medium subangular blocky structure; friab"| __truncated__ "Bw3--26 to 38 inches; brown (7.5YR 4/4) loam; weak medium subangular blocky structure; friable; common fine roo"| __truncated__ ... ## .. .. ..$ hzID : chr [1:22] "1" "2" "3" "4" ... ## .. ..@ site :'data.frame': 3 obs. of 33 variables: ## .. .. ..$ id : chr [1:3] "CHEWACLA" "CONGAREE" "WILKES" ## .. .. ..$ soiltaxclasslastupdated: chr [1:3] "2010-02-11 00:00:00+00" "2002-07-18 00:00:00+00" "1997-06-06 00:00:00+00" ## . . .. ..$ mlraoffice : chr [1:3] "raleigh, nc" "raleigh, nc" "raleigh, nc" ## .. .. ..$ series_status : chr [1:3] "established" "established" "established" ## .. .. ..$ family : chr [1:3] "fine-loamy, mixed, active, thermic fluvaquentic dystrudepts" "fine-loamy, mixed, active, nonacid, thermic oxyaquic udifluvents" "loamy, mixed, active, thermic, shallow typic hapludalfs" ## .. .. ..$ soilorder : chr [1:3] "inceptisols" "entisols" "alfisols" ## .. .. ..$ suborder : chr [1:3] "udepts" "fluvents" "udalfs" ## .. .. ..$ greatgroup : chr [1:3] "dystrudepts" "udifluvents" "hapludalfs" ## .. .. ..$ subgroup : chr [1:3] "fluvaquentic dystrudepts" "oxyaquic udifluvents" "typic hapludalfs" ## .. .. ..$ tax_partsize : chr [1:3] "fine-loamy" "fine-loamy" "loamy" ## .. .. ..$ tax_partsizemod : logi [1:3] NA NA NA ## .. .. ..$ tax_ceactcl : chr [1:3] "active" "active" "active" ## . . .. ..$ tax_reaction : chr [1:3] NA "nonacid" NA ## .. .. ..$ tax_tempcl : chr [1:3] "thermic" "thermic" "thermic" ## .. .. ..$ originyear : logi [1:3] NA NA NA ## .. .. ..$ establishedyear : int [1:3] 1937 1904 1916 ## .. .. ..$ descriptiondateinitial : chr [1:3] "2010-02-11 00:00:00+00" "2002-07-18 00:00:00+00" "2007-09-06 00:00:00+00" ## .. .. ..$ descriptiondateupdated : chr [1:3] "2010-02-11 00:00:00+00" "2002-07-18 00:00:00+00" "2021-01-27 16:02:50+00" ## .. .. ..$ benchmarksoilflag : int [1:3] 1 0 0 ## .. .. ..$ statsgoflag : int [1:3] 1 1 1 ## .. .. ..$ objwlupdated : chr [1:3] "2012-08-01 14:06:37+00" "2012-08-01 14:06:37+00" "2021-01-27 16:02:50+00" ## .. .. ..$ recwlupdated : chr [1:3] "2012-08-01 14:06:37+00" "2012-08-01 14:06:37+00" "2021-01-27 16:02:50+00" ## .. .. ..$ typelocstareaiidref : int [1:3] 6691 6706 6691 ## .. .. ..$ typelocstareatypeiidref: int [1:3] 3 3 3 ## . . .. ..$ soilseriesiid : int [1:3] 24628 1057 23800 ## .. .. ..$ soilseriesdbiidref : int [1:3] 122 122 122 ## .. .. ..$ grpiidref : int [1:3] 15801 15801 15801 ## .. .. ..$ tax_minclass : chr [1:3] "mixed" "mixed" "mixed" ## .. .. ..$ subgroup_mod : chr [1:3] "fluvaquentic" "oxyaquic" "typic" ## .. .. ..$ greatgroup_mod : chr [1:3] "dystr" "udi" "hapl" ## .. .. ..$ drainagecl : chr [1:3] "somewhat poorly" "well to moderately well" "well" ## .. .. ..$ ac : int [1:3] 1256820 216072 614614 ## .. .. ..$ n_polygons : int [1:3] 39164 10384 34815 ## .. ..@ sp :Formal class 'SpatialPoints' [package "sp"] with 3 slots ## .. .. .. ..@ coords : num [1, 1] 0 ## .. .. .. ..@ bbox : logi [1, 1] NA ## .. .. .. ..@ proj4string:Formal class 'CRS' [package "sp"] with 1 slot ## .. .. .. .. .. ..@ projargs: chr NA ## .. ..@ diagnostic :'data.frame': 0 obs. of 0 variables ## . . ..@ restrictions:'data.frame': 0 obs. of 0 variables ## $ competing :'data.frame': 1 obs. of 3 variables: ## ..$ series : chr "CHEWACLA" ## ..$ competing: chr "OAKBORO" ## ..$ family : chr "fine-loamy, mixed, active, thermic fluvaquentic dystrudepts" ## $ geog_assoc_soils:'data.frame': 22 obs. of 2 variables: ## ..$ series: chr [1:22] "CONGAREE" "CONGAREE" "CONGAREE" "CONGAREE" ... ## ..$ gas : chr [1:22] "ALTAVISTA" "AUGUSTA" "BUNCOMBE" "CARTECAY" ... ## $ geomcomp :'data.frame': 3 obs. of 9 variables: ## ..$ series : chr [1:3] "CHEWACLA" "CONGAREE" "WILKES" ## ..$ Interfluve : num [1:3] 1 0 0.178 ## ..$ Crest : num [1:3] 0 0 0.027 ## ..$ Head Slope : int [1:3] 0 0 0 ## ..$ Nose Slope : int [1:3] 0 0 0 ## ..$ Side Slope : num [1:3] 0 0 0.795 ## ..$ Base Slope : int [1:3] 0 1 0 ## ..$ n : int [1:3] 3 1 185 ## ..$ shannon_entropy: num [1:3] 0 0 0.365 ## $ hillpos :'data. frame': 3 obs. of 8 variables: ## ..$ series : chr [1:3] "CHEWACLA" "CONGAREE" "WILKES" ## ..$ Toeslope : num [1:3] 0.963 0.786 0 ## ..$ Footslope : num [1:3] 0.0366 0.2143 0 ## ..$ Backslope : num [1:3] 0 0 0.637 ## ..$ Shoulder : num [1:3] 0 0 0.225 ## ..$ Summit : num [1:3] 0 0 0.139 ## ..$ n : int [1:3] 82 14 245 ## ..$ shannon_entropy: num [1:3] 0.0975 0.3228 0.5573 ## $ mtnpos : logi FALSE ## $ terrace :'data.frame': 2 obs. of 5 variables: ## ..$ series : chr [1:2] "CHEWACLA" "CONGAREE" ## ..$ Tread : num [1:2] 0.977 1 ## ..$ Riser : num [1:2] 0.023 0 ## ..$ n : int [1:2] 87 36 ## ..$ shannon_entropy: num [1:2] 0.068 0 ## $ flats :'data.frame': 2 obs. of 7 variables: ## ..$ series : chr [1:2] "CHEWACLA" "CONGAREE" ## ..$ Dip : num [1:2] 0.1455 0.0667 ## ..$ Talf : num [1:2] 0.855 0.867 ## . .$ Flat : int [1:2] 0 0 ## ..$ Rise : num [1:2] 0 0.0667 ## ..$ n : int [1:2] 55 15 ## ..$ shannon_entropy: num [1:2] 0.258 0.301 ## $ pmkind :'data.frame': 6 obs. of 5 variables: ## ..$ series: chr [1:6] "CHEWACLA" "CHEWACLA" "CONGAREE" "CONGAREE" ... ## ..$ pmkind: chr [1:6] "Alluvium" "Residuum" "Alluvium" "Fluviomarine deposits" ... ## ..$ n : int [1:6] 206 1 72 13 1 262 ## ..$ total : int [1:6] 207 207 86 86 86 262 ## ..$ P : num [1:6] 0.9952 0.0048 0.8372 0.1512 0.0116 ... ## $ pmorigin :'data.frame': 24 obs. of 5 variables: ## ..$ series : chr [1:24] "CHEWACLA" "CHEWACLA" "CHEWACLA" "CHEWACLA" ... ## ..$ pmorigin: chr [1:24] "Igneous and metamorphic rock" "Sedimentary rock" "Mixed" "Granite and gneiss" ... ## ..$ n : int [1:24] 29 11 2 2 1 1 1 1 1 1 ... ## ..$ total : int [1:24] 51 51 51 51 51 51 51 51 51 51 ... ## ..$ P : num [1:24] 0.5686 0.2157 0.0392 0.0392 0.0196 ... ## $ mlra :'data.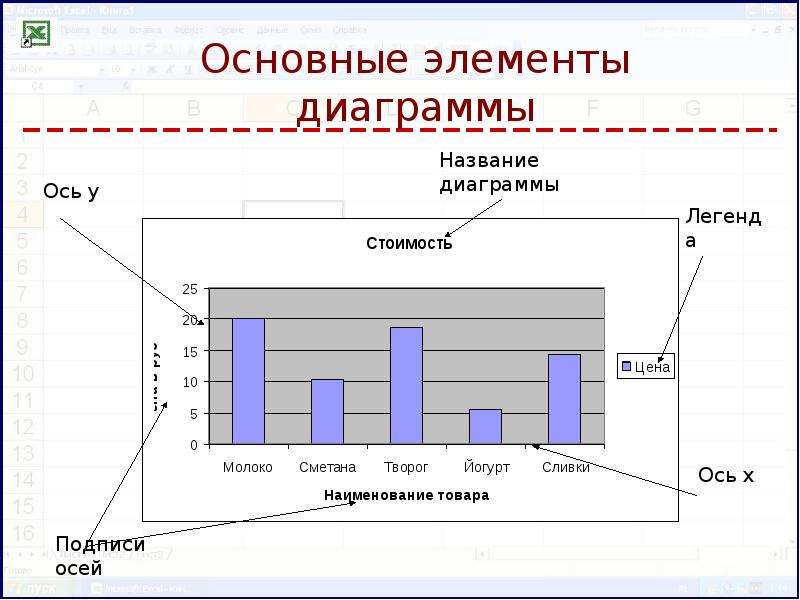 frame': 19 obs. of 4 variables: ## ..$ series : chr [1:19] "CHEWACLA" "CHEWACLA" "CHEWACLA" "CHEWACLA" ... ## ..$ mlra : chr [1:19] "129" "135A" "136" "133A" ... ## ..$ area_ac : int [1:19] 6166 3878 927251 128381 78428 60214 29004 13536 9495 2126 ... ## ..$ membership: num [1:19] 0.005 0.003 0.738 0.102 0.062 0.048 0.023 0.011 0.008 0.01 ... ## $ climate.annual :'data.frame': 24 obs. of 12 variables: ## ..$ series : chr [1:24] "CHEWACLA" "CHEWACLA" "CHEWACLA" "CHEWACLA" ... ## ..$ climate_var: chr [1:24] "Elevation (m)" "Effective Precipitation (mm)" "Frost-Free Days" "Mean Annual Air Temperature (degrees C)" ... ## ..$ minimum : num [1:24] 0 128.8 177 11.3 986 ... ## ..$ q01 : num [1:24] 7 216.4 188 12.9 1069 ... ## ..$ q05 : num [1:24] 34 247.4 196 13.5 1093 ... ## ..$ q25 : num [1:24] 125 312.2 208 14.9 1136 ... ## ..$ q50 : num [1:24] 192 349.8 218 15.7 1178 ... ## ..$ q75 : num [1:24] 248 441.2 227 16. 4 1276 ... ## ..$ q95 : num [1:24] 348 568.8 235 17.3 1392 ... ## ..$ q99 : num [1:24] 480 740.8 243 17.8 1575 ... ## ..$ maximum : num [1:24] 919 1382.8 300 19.7 2202 ... ## ..$ n : int [1:24] 32689 32689 32689 32689 32689 32689 32689 32689 8392 8392 ... ## $ climate.monthly :'data.frame': 72 obs. of 14 variables: ## ..$ series : chr [1:72] "CHEWACLA" "CHEWACLA" "CHEWACLA" "CHEWACLA" ... ## ..$ climate_var: chr [1:72] "ppt1" "ppt2" "ppt3" "ppt4" ... ## ..$ minimum : num [1:72] 61 64 81 63 60 78 83 74 68 53 ... ## ..$ q01 : num [1:72] 74 71 92 71 69 83 92 85 81 72 ... ## ..$ q05 : num [1:72] 82 73 98 75 72 89 100 89 86 76 ... ## ..$ q25 : num [1:72] 93 83 105 83 81 96 108 96 91 82 ... ## ..$ q50 : num [1:72] 105 107 120 88 92 101 116 102 98 86 ... ## ..$ q75 : num [1:72] 115 121 128 95 101 106 123 110 105 91 ... ## ..$ q95 : num [1:72] 131 135 137 111 111 117 133 129 118 100 ... ## .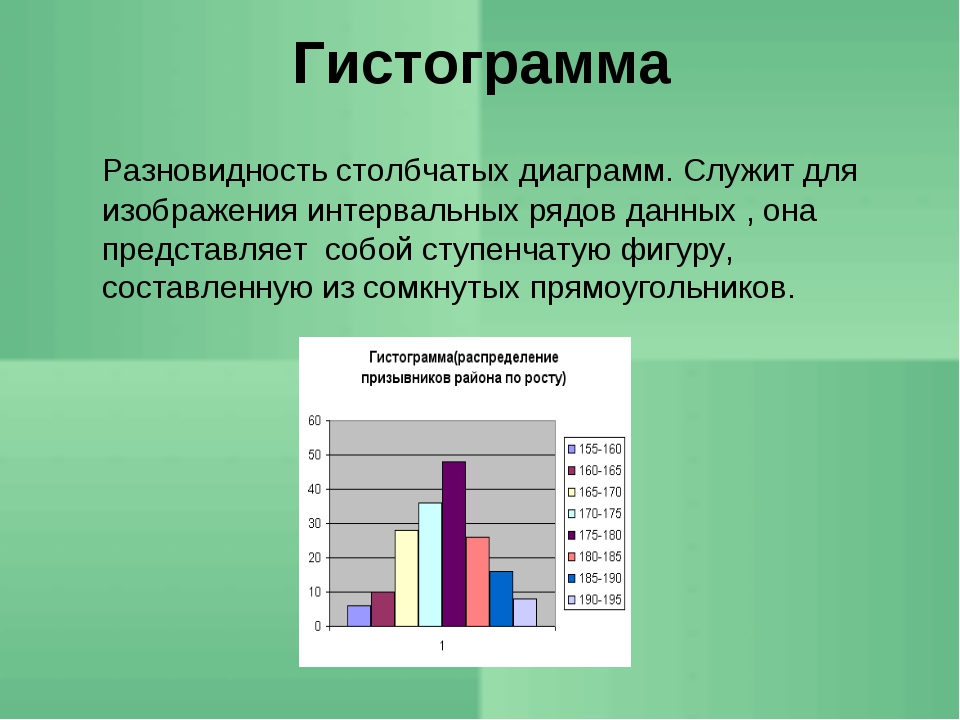 .$ q99 : num [1:72] 149 144 147 122 125 133 143 142 137 109 ... ## ..$ maximum : num [1:72] 248 227 239 150 167 198 220 207 192 158 ... ## ..$ n : int [1:72] 32689 32689 32689 32689 32689 32689 32689 32689 32689 32689 ... ## ..$ month : Factor w/ 12 levels "1","2","3","4",..: 1 2 3 4 5 6 7 8 9 10 ... ## ..$ variable : Factor w/ 2 levels "Potential ET (mm)",..: 2 2 2 2 2 2 2 2 2 2 ... ## $ soilweb.metadata:'data.frame': 18 obs. of 2 variables: ## ..$ product : chr [1:18] "block diagram archive" "cached sketches" "component pedons" "KSSL snapshot" ... ## ..$ last_update: chr [1:18] "2019-12-17" "2021-10-07" "2020-12-08" "2020-03-18" ... Базовый шаблон ggplot Для начала посмотрим, как можно показать суммарный экспорт по годам: Базовый (минимально необходимый) шаблон построения графика через ggplot выглядит следующим образом: ggplot(data = <DATA>) + <GEOM_FUNCTION>(mapping = aes(<MAPPINGS>)) где: DATA — источник данных (фрейм, тиббл) GEOM_FUNCTION — функция, отвечающая за геометрический тип графика (точки, линии, гистограммы и т. д.) MAPPINGS — перечень соответствий между переменными данных (содержащихся в DATA) и графическими переменными (координатами, размерами, цветами и т.д.) Геометрические типы и преобразования ggplot предлагает несколько десятков различных видов геометрий для отображения данных. С их полным перечнем можно познакомиться тут. Мы рассмотрим несколько наиболее употребительных, а геометрии, связанные со статистическими преобразованиями, оставим для следующей темы. В первом примере мы отображали данные по экспорту за разные года, однако точечный тип не очень подходит для данного типа графика, поскольку он показывает динамику изменения. А это означает, что желательно соединить точки линиями. Для этого используем геометрию geom_line(): Поскольку в данном случае величина является агрегированной за год, более правильным может быть показ ее изменений в виде ступенчатого линейного графика, который получается через геометрию geom_step(): Можно совместить несколько геометрий, добавив их последовательно на график: Если у нескольких геометрий одинаковые отображения, их можно вынести в вызов функции ggplot() (чтобы не дублировать): Наглядность линейного графика можно усилить, добавив “заливку” области с использованием geom_area(): Для построения столбчатой диаграммы следует использовать геометрию geom_col(). Например, вот так выглядит структура экспорта продукции машиностроения из Евросоюза по ведущим партнерам: trades |> dplyr::filter(sitc06 == 'Machinery and transport equipment', time == as.Date('2017-01-01')) |> ggplot(mapping = aes(x = partner, y = export)) + geom_col() Развернуть диаграмму можно, используя функцию coord_flip(): Графические переменные и группировки Графические переменные — это параметры, определяющие внешний вид символов. К ним относятся цвет (тон, насыщенность и светлота), размер, форма, ориентировка, внутренняя структура символа. В ggplot значения графических переменных могут быть едиными для всех измерений, а могут зависеть от величины измерений. С точки зрения управления здесь все просто: если вы хотите, чтобы какой-то графический параметр зависел от значения показателя, он должен быть указан внутри конструкции mapping = aes(...). Если необходимо, чтобы этот параметр был одинаковым для всех измерений, вы должны его указать внутри <GEOM_FUNCTION>(.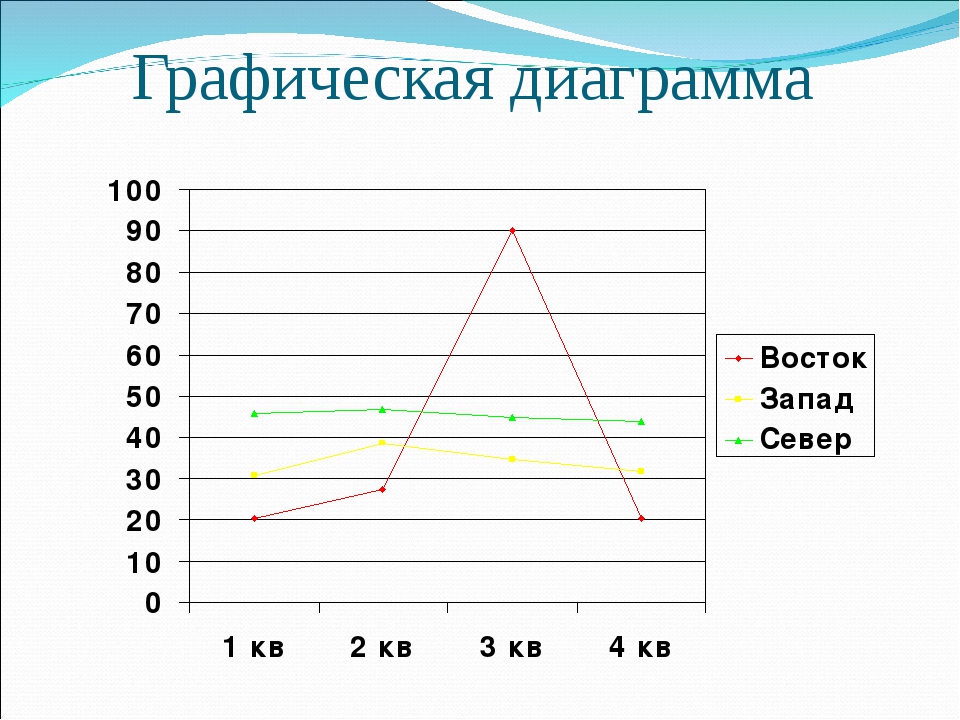 ..), то есть не передавать в mapping. Для управления цветом, формой и размером (толщиной) графического примитива следует использовать параметры color, shape и size соответственно. Посмотрим, как они работают внутри и за пределами функции aes(): # один цвет для графика (параметр за пределами aes) ggplot(trades_total) + geom_line(mapping = aes(x = time, y = export), color = 'blue') trade_russia = trades |> dplyr::filter(partner == 'Russia') ggplot(trade_russia) + # у каждой группы данных свой цвет (параметр внутри aes) geom_line(mapping = aes(x = time, y = export, color = sitc06)) ggplot(trade_russia, mapping = aes(x = time, y = export, color = sitc06)) + # а теперь и с точками geom_line() + geom_point() Аналогичным образом работает параметр формы значка: # один значок для графика ggplot(trades_total) + geom_point(mapping = aes(x = time, y = export), shape = 15) ggplot(trade_russia) + # у каждой группы данных свой значок geom_point(mapping = aes(x = time, y = export, shape = sitc06)) Для изменения размера значка или линии используйте параметр size: # изменение размера значка и линии ggplot(trades_total, mapping = aes(x = time, y = export)) + geom_point(size = 5) + geom_line(size = 2) Если вы используете зависимые от значений графические переменные и при этом хотите добавить на график еще одну геометрию (c постоянными параметрами), то вам необходимо сгруппировать объекты второй геометрии по той же переменной, по которой вы осуществляете разбиение в первой геометрии. Для этого используйте параметр group: Для изменения цвета столбчатых диаграмм следует использовать параметр fill, а цвет и толщина обводки определяются параметрами color и size: trades |> dplyr::filter(sitc06 == 'Machinery and transport equipment', time == as.Date('2017-01-01')) |> ggplot(mapping = aes(x = partner, y = export)) + geom_col(fill = 'plum4', color = 'black', size = 0.2) + coord_flip() Цвет на столбчатых диаграммах можно использовать для отображения дополнительных переменных, например типа экспортируемой продукции. По умолчанию столбики будут образовывать стек Если вам важно не абсолютное количество, а процентное соотношение величин, вы можете применить вид группировки position == 'fill: Еще один вид группировки — это группировка по соседству. Чтобы использовать ее, применить метод position == 'dodge: trade_russia |> dplyr::filter(time >= as. Date('2013-01-01')) |> ggplot(mapping = aes(x = time, y = export, fill = sitc06)) + geom_col(color = 'black', size = 0.2, position = 'dodge') Системы координат ggplot поддерживает множество полезных преобразований координат, таких как смена осей X и Y, переход к логарифмическим координатам и использование полярной системы вместо декартовой прямоугольной. Смена переменных происходит благодаря уже знакомой нам функции coord_flip(). Рассмотрим, например, как изменилась структура экспорта/импорта по годам: trades_type = trades |> group_by(sitc06, time) |> summarise(export = sum(export), import = sum(import)) ggplot(trades_type) + geom_point(mapping = aes(x = export, y = import, color = sitc06, size = time), alpha = 0.5) Поскольку объемы продукции различаются на порядки, для различимости малых объемов целесообразно перейти к логарифмической шкале. Для этого используем scale_log_x() и scale_log_y(): Преобразование в полярную систему координат используется для того чтобы получить круговую секторную диаграмму Найтингейл (coxcomb chart): Разумеется, здесь тоже можно использовать преобразование шкалы по оси Y (которая теперь отвечает за радиус). Применим правило квадратного корня, добавив вызов функции scale_y_sqrt(): Чтобы построить классическую секторную диаграмму, необходимо, чтобы угол поворота соответствовал величине показателя (оси Y), а не названию категории (оси X). Для этого при вызове функции coord_polar() следует указать параметр theta = 'y', а при вызове geom_col() оставить параметр x пустым: trades |> dplyr::filter(sitc06 == 'Machinery and transport equipment', time == as.Date('2017-01-01')) |> ggplot(mapping = aes(x = '', y = export, fill = partner), color = 'black', size = 0. 2) + geom_col() + coord_polar(theta = 'y') Названия осей и легенды ggplot предоставляет ряд функций для аннотирования осей и легенды. Для этого можно использовать одну из следующих функций: labs(...) модифицирует заголовок легенды для соответствующей графической переменной, либо заголовок/подзаголовок графика xlab(label) модифицирует подпись оси X ylab(label) модифицирует подпись оси Y ggtitle(label, subtitle = NULL) модифицирует заголовок и подзаголовок графика Создадим подписи легенд, отвечающих за цвет и размер значка на графике соотношения импорта и экспорта разных видов продукции: ggplot(trades_type) + geom_point(mapping = aes(x = export, y = import, color = sitc06, size = time), alpha = 0.5) + labs(color = "Вид продукции", size = 'Год') Добавим заголовок и подзаголовок графика: ggplot(trades_type) + geom_point(mapping = aes(x = export, y = import, color = sitc06, size = time), alpha = 0. 5) + labs(color = "Вид продукции", size = 'Год') + ggtitle('Соотношение импорта и экспорта в странах Евросоюза (млн долл. США)', subtitle = 'Данные по ключевым партнерам') Изменим подписи осей: ggplot(trades_type) + geom_point(mapping = aes(x = export, y = import, color = sitc06, size = time), alpha = 0.5) + labs(color = "Вид продукции", size = 'Год') + ggtitle('Соотношение импорта и экспорта в странах Евросоюза (млн долл. США)', subtitle = 'Данные по ключевым партнерам') + xlab('Экспорт') + ylab('Импорт') Разметка осей Первое, что вам скорее всего захочется убрать — это экспоненциальная запись чисел. На самом деле, эта запись не является параметром ggplot или стандартной системы graphics. Количество значащих цифр, после которых число автоматически представляется в экспоненциальном виде, управляется параметром scipen. Мы можем задать его достаточно большим, чтобы запретить переводить любые разумные числа в экспоненциальный вид: options(scipen = 999) ggplot(trades_type) + geom_point(mapping = aes(x = export, y = import, color = sitc06, size = time), alpha = 0. 5) + labs(color = "Вид продукции", size = 'Год') + ggtitle('Соотношение импорта и экспорта в странах Евросоюза (млн долл. США)', subtitle = 'Данные по ключевым партнерам') + xlab('Экспорт') + ylab('Импорт') Для управления разметкой осей необходимо использовать функции scale_x_continuous(), scale_y_continuous(), scale_x_log10(...), scale_y_log10(...), scale_x_reverse(...), scale_y_reverse(...), scale_x_sqrt(...), scale_y_sqrt(...), которые, с одной стороны, указывают тип оси, а с другой стороны — позволяют управлять параметрами сетки координат и подписями. Для изменения координат линий сетки и подписей необходимо использовать, соответственно, параметры breaks и labels: В данном случае, как раз, будет достаточно полезным параметр labels, поскольку метки можно сделать более компактными, поделив их на 1000 (и не забыть потом указать, что объемы теперь указаны не в миллионах, а в миллиардах долларов): brks = seq(0, 500000, 100000) ggplot(trades_type, mapping = aes(x = export, y = import, color = sitc06, size = time)) + geom_point(alpha = 0. 5) + scale_x_log10(breaks = brks, labels = brks / 1000) + scale_y_log10(breaks = brks, labels = brks / 1000) Для обычной шкалы используйте функции scale_x_continuous() и scale_y_continuous(): Для того чтобы принудительно указать диапазоны осей и графических переменных, следует использовать функции lims(...), xlim(...) и ylim(...). Например, мы можем приблизиться в левый нижний угол графика, задав диапазон 0-200000 по обеим осям: ggplot(trades_type, mapping = aes(x = export, y = import, color = sitc06, size = time)) + geom_point(alpha = 0.5) + xlim(0, 75000) + ylim(0, 75000) Функция lims() работает еще хитрее: она позволяет применять графические переменные только к ограниченному набору значений исходных данных. Например, таким путем я могу выделить на графике продукцию машиностроения: ggplot(trades_type, mapping = aes(x = export, y = import, color = sitc06, size = time)) + geom_point(alpha = 0. 5) + lims(color = 'Machinery and transport equipment') Подписи и аннотации С точки зрения ggplot текст на графике, отображающий входные данные, является одной из разновидностей геометрии. Размещается он с помощью функции geom_text(). Как и в случае с другими геометриями, параметры, зависящие от исходных данных, должны быть переданы внутри mapping = aes(...): Выравнивание подписи относительно якорной точки (снизу, сверху, справа, слева) по горизонтали и вертикали управляется параметрами hjust и vjust, а смещения по осям X (в координатах графика) — параметрами nudge_x и nudge_y: ggplot(data = trades_total, mapping = aes(x = time, y = export)) + geom_area(alpha = 0.5) + # полигон с прозрачностью 0,5 geom_line() + geom_point() + geom_text(aes(label = floor(export / 1000)), vjust = 0, nudge_y = 40000) # добавляем подписи Подписи с фоновой плашкой добавляются через функцию geom_label(), которая имеет аналогичный синтаксис: trades |> dplyr::filter(sitc06 == 'Machinery and transport equipment', time == as. Date('2017-01-01')) |> ggplot(mapping = aes(x = partner, y = export)) + geom_col(fill = 'plum4', color = 'black', size = 0.2) + coord_flip() + geom_label(aes(y = export / 2, label = floor(export / 1000))) # добавляем подписи Аннотации представляют собой объекты, размещаемые на графике вручную, и используемые, как правило, для выделения объектов и областей. Для размещения аннотаций используется функция annotate(): ggplot(data = trades_total, mapping = aes(x = time, y = export)) + geom_area(alpha = 0.5) + # полигон с прозрачностью 0,5 geom_line() + geom_point() + geom_text(aes(label = floor(export / 1000)), vjust = 0, nudge_y = 40000) + annotate("text", x = as.Date('2009-01-01'), y = 550000, label = "Это провал", color = 'red') Аннотировать можно не только подписями, но и регионами. Например, мы можем выделить область, которая соответствует импорту/экспорту продукции химической промышленности: ggplot(trades_type, mapping = aes(x = export, y = import, color = sitc06, size = time)) + annotate("rect", xmin = 100000, xmax = 250000, ymin = 75000, ymax = 175000, alpha = . 2, color = 'black', size = 0.1) + geom_point(alpha = 0.5) + annotate("text", x = 175000, y = 190000, label = "Chemicals", color = 'coral') Фасеты Фасеты представляют собой множество графиков, каждый из которых отображает свою переменную или набор значений. Для разбиения на фасеты используется функция facet_wrap(), которой необходимо передать переменную разбиения с тильдой. Например, рассмотрим изменение структуры импорта по годам: brks = c(0, 50, 100, 150, 200) trades |> dplyr::filter(sitc06 == 'Machinery and transport equipment') |> ggplot(mapping = aes(x = partner, y = import)) + geom_col() + scale_y_continuous(breaks = brks * 1e3, labels = brks) + ggtitle('Импорт продукции машиностроения (мдрд долл. США)', subtitle = 'Данные по ключевым партнерам') + coord_flip() + facet_wrap(~time) Темы Система ggplot интересна также тем, что для нее существует множество предопределенных “тем” или скинов для оформления графиков. Часть из них входит в состав самой библиотеки. Дополнительные темы можно установить через пакет ggthemes. Чтобы изменить тему оформления ggplot, достаточно прибавить в конце построения графика соответствующую функцию. Например, классическая черно-белая тема получается прибавлением функции theme_bw(): ggplot(trades_type) + geom_point(mapping = aes(x = export, y = import, color = sitc06, size = time), alpha = 0.5) + labs(color = "Вид продукции", size = 'Год') + ggtitle('Соотношение импорта и экспорта в странах Евросоюза (млн долл. США)', subtitle = 'Данные по ключевым партнерам') + xlab('Экспорт') + ylab('Импорт') + theme_bw() Краткий обзор Для просмотра презентации щелкните на ней один раз левой кнопкой мыши и листайте, используя кнопки на клавиатуре: Презентацию можно открыть в отдельном окне или вкладке браузере. Для этого щелкните по ней правой кнопкой мыши и выберите соответствующую команду. Контрольные вопросы и упражнения Вопросы Назовите три основных компоненты шаблона построения графика в ggplot2. Как называются геометрии ggplot2, отвечающие за построение точек, линий и ступенчатых линий? Как называется геометрия ggplot2, отвечающая за построение столбчатой диаграммы? Как сделать так, чтобы графический параметр ggplot2 был постоянным для всех измерений? Как сделать так, чтобы графический параметр ggplot2 зависел от значения переменной? Перечислите названия параметров, отвечающих за цвет, размер, заливку и тип значка графического примитива. Если вы используете зависимые от значений графические переменные и при этом хотите добавить на график еще одну геометрию с постоянными параметрами, то как это можно реализовать? Перечислите названия режимов группировки столбчатых диаграмм и пути их реализации. Какая функция ggplot2 позволяет поменять местами оси координат? Перечислите типы шкал для осей координат, которые доступны в ggplot2. Назовите функцию, позволяющую перейти к полярной системе координат при построении графика в ggplot2. В чем отличие построения розы-диаграммы (coxcomb chart) и секторной диаграммы (pie chart) средствами ggplot2? Что делает функция labs()? Какие функции позволяют определить названия осей и заголовок графика? Что делает функция lims()? Как ограничить область построения графика заданным диапазоном значений координат? Как ограничить применение графических переменных только к определенным значениям измерений? Назовите геометрии, которые позволяют размещать подписи и подписи с плашками (фоном) на графиках ggplot2. Чем отличаются аннотации от геометрии подписей в ggplot? Какие виды аннотаций можно создавать? Каким образом можно построить фасетный график, на котором каждое изображение соответствует значению переменной? Каков синтаксис вызова соответствующей функции? Как поменять стиль отображения (тему) графика ggplot2? Как получить программный доступ к таблицам Евростата, не прибегая к закачке файлов? Какой пакет можно использовать для этого? Что является уникальным идентификатором таблицы в данных Евростата и как его узнать? Как преобразовать коды Евростата в загруженных таблицах в человеко-читаемые обозначения? Упражнения Упражнения данной главы частично повторяют упражнения предыдущей главы по базовой графике в целях сравнения двух графических систем R. Постройте для набора данных quakes пакета datasets гистограммы распределения глубин и магнитуд, а также диаграмму рассеяния для двух этих характеристик. Используйте сначала функцию qplot(), а затем выполните то же самое с использованием полного синтаксиса ggplot2(). На портале открытых данных Тульской области есть данные о распределении площади лесов и запасов древесины по преобладающим породам и группам возраста. Скачайте эти данные в виде таблицы CSV и постройте по ним круговую и столбчатую диаграмму для категории Площадь земель, занятых лесными насаждениями (покрытых лесной растительностью), всего. Подберите цвета, попробуйте изменить ориентировку столбцов на горизонтальную, а для круговой диаграммы поменять угол поворота. Используя данные по балансу масс ледника Гарабаши, постройте график с тремя кривыми (аккумуляции, абляции и кумулятивного баланса) за период 1981 по 2017 г.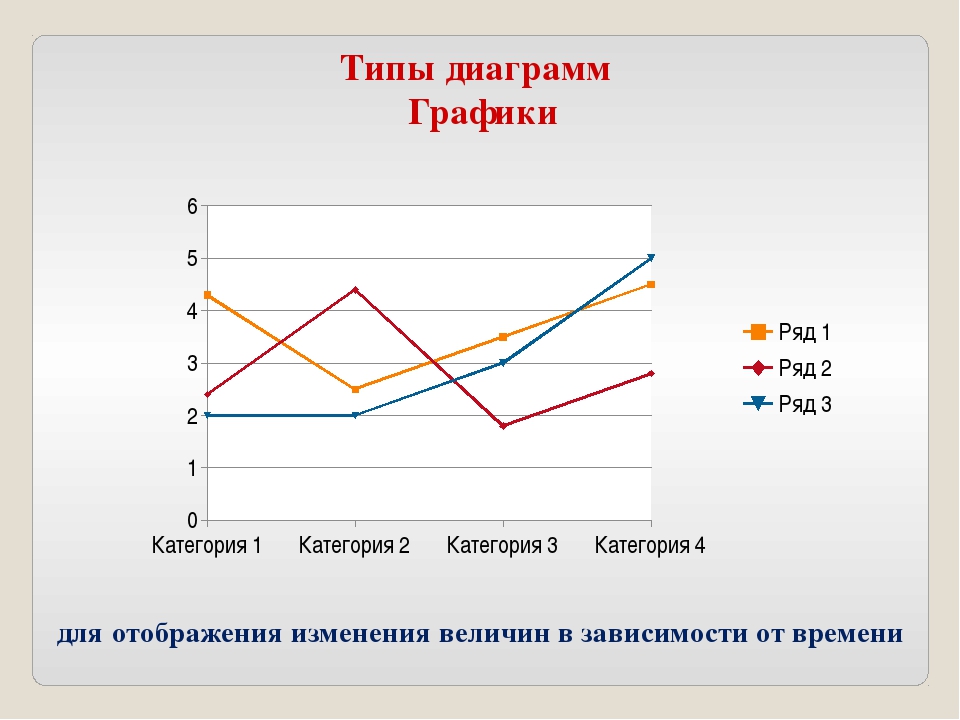 Добавьте на график легенду. Обратите внимание на то, что таблица содержит агрегирующие строки (1982-1997, 1998-2017, 1982-2017), которые вам необходимо предварительно исключить. Подсказка: Чтобы построить кривую кумулятивного баланса, используйте функцию cumsum. Загрузите таблицу данных по импорту/экспорту продуктов питания, напитков и табака с портала Евростата (с использованием пакета eurostat). Постройте линейный график изменения суммарных величин импорта и экспорта по данному показателю (у вас должно получиться 2 графика на одном изображении). Используйте цвет для разделения графиков. Добавьте текстовые подписи величин импорта и экспорта. Постройте также две круговых диаграммы, показывающих соотношение ведущих импортеров и экспортеров за последний имеющийся год. Сделайте сначала это отдельными графиками, а затем одним фасетным графиком (для этого потребуется привести таблицу к длинной форме). Постройте линейный график хода температуры , а также столбчатую диаграмму хода суммарной солнечной радиации в Екатеринбурге на примере данных NASA POWER, загруженных в разделе 6.3. Подсказка: Для построения столбчатой диаграммы вам потребуется использовать функцию geom_col(), поскольку высота столбика отражает не встречаемость значения, а величину переменной. Также вам потребуется преобразовать таблицу среднемесячных величин к длинной форме, где название месяца будет отдельной переменной (тип — упорядоченный фактор). Самсонов Т.Е. Визуализация и анализ географических данных на языке R. М.: Географический факультет МГУ, 2021. DOI: 10.5281/zenodo.901911 Рисунки, графики, диаграммы, схемы в работах студентов Еще одним традиционным способом представления экспериментальных данных в научной публикации является их графическое изображение. Чаще всего, оно используется в статье, очень редко, при создании тезисов и реферата и никогда, в резюме и аннотации. Это изображение, обязательно сопровождается соответствующим текстом, объясняющего особенности его экспериментального происхождения и информационного предназначения. Адекватное зрительное представление полученных данных способно более наглядно (по сравнению, только с текстом или таблицей) продемонстрировать различия, тенденцию изменения, характер взаимосвязей и сам факт существования изучаемых показателей. Информационная суть таких изображений может отражать или количественные характеристики, полученные с помощью измерений, или качественные особенности, в виде демонстрации визуальных характеристик исследуемого показателя (например, с помощью фотографии или «художественного изображения»). Что касается информационного предназначения, то оно обусловлено намерениями автора обратить внимание читателя на определенные особенности полученных результатов. Это намерение может заключаться в желании продемонстрировать или сам факт появления изменений, или их величину, или тенденцию, или вид зависимости и т. п.Авторский выбор такого предназначения определяет, какой вид графического изображения рациональнее всего использовать для этого, чтобы наиболее аргументировано доказать или решение конкретной научной задачи, или достижение научной цели исследования. Обычно, для графического представления результатов применяют графики (1), гистограммы (2), диаграммы (3), схемы (4), рисуночные изображения (5) и фотографии (6). Как правило, первые три из этих видов представления создаются на основе соответствующих таблиц (не обязательно приведенных в статье), где представлены количественные значения (точечные или усредненные) первичных данных. Эти значения могут изменяться или под влиянием разных экспериментальных условий, или во времени, или под воздействием разных интенсивностей одного и того же контролируемого фактора, или отражать взаимосвязь двух показателей. С помощью четвертого вида можно наглядно продемонстрировать методические, логические процедуры научного подхода, условия эксперимента и т.п. А остальные виды (5 и 6), в основном, используются для доказательства самого факта получения (возникновения) качественного результата, который не может быть количественно измерен, или для демонстрации внешнего вида исследовательской аппаратуры, анкет, вопросников и т.п. В процессе создания научной публикации все перечисленные виды графического представления данных рекомендуется готовить с помощью соответствующих «программных мастеров» редактора «Word» или «Excel». Практически удобно это делать в специальном файле (например, «Рисунки») или в отдельном файле для каждого рисунка с соответствующим названием (например, Рисунок 1). Это связано с тем, что согласно общепринятой публикационной терминологии, «рисунком» называется любое графическое изображении, приведенное в статье, начиная со схемы и заканчивая традиционным «художественным» рисунком (фотографией). Именно, поэтому в научной статье всегда используется только термин «рисунок» и к графику, и к гистограмме, и к диаграмме, и к схеме, и к «художественному изображению», и к фотографии.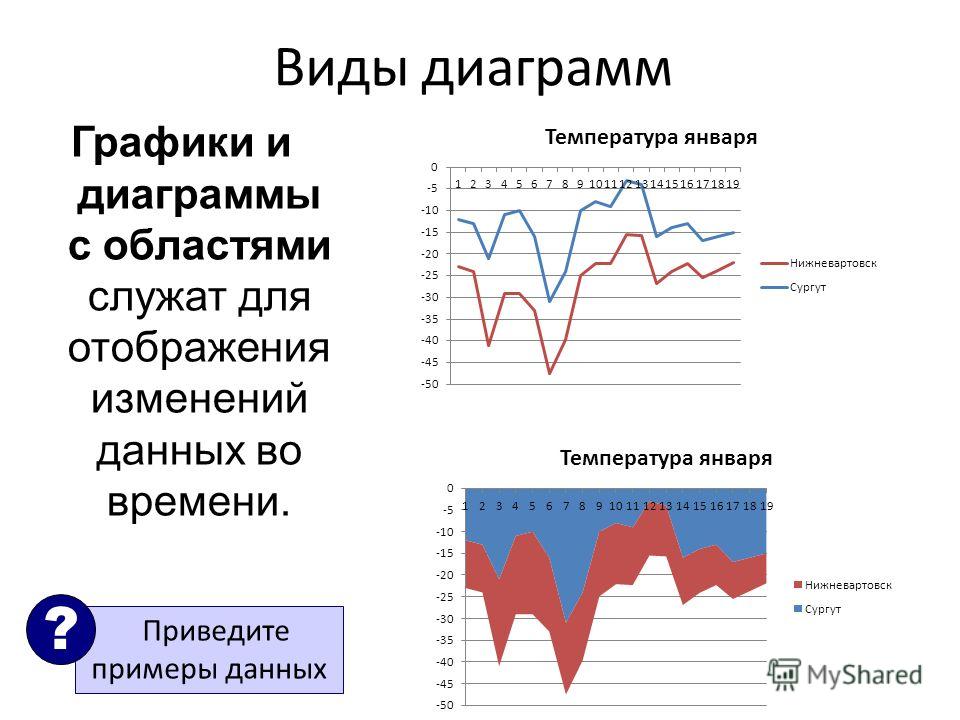 Ссылка на такой рисунок, обычно, приводится в круглых скобках с сокращением этого слова, например, (Рис.1), сразу же после первого упоминания о нем в тексте, в виде соответствующих сведений, с последующим предоставлением самого рисунка. При создании «статейных рисунков», желательно, каждое отдельное графическое изображение, независимо от его разновидности, располагать на одной отдельной странице с возможностью копирования и вставки в нужное место текста. Наиболее целесообразно это делать после напечатания всей статьи, копируя нужный рисунок (из его файла) на новую страницу после той, где на него ссылаются впервые. Но можно вставлять рисунок и сразу же после конкретного предложения, в котором приводятся данные, представленные на нем, и соответствующая ссылка. Правда, это потребует последующего специального редактирования текста на странице, до и после вставленного рисунка. Поэтому, все же, несмотря на то, что ссылка на рисунок представлена на одной странице сам, заранее подготовленный в отдельном файле рисунок, предпочтительнее размещать вне текста, сразу же на следующей отдельной странице.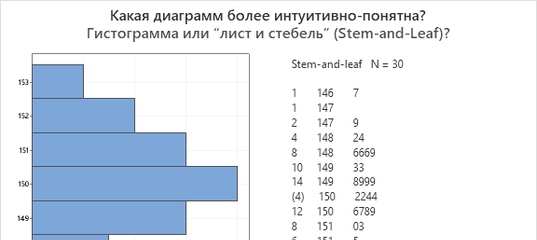 А после ссылки на него на предыдущей странице, просто, продолжить тестовое описание других результатов. При такой компоновке, на одной странице может быть ссылки на несколько рисунков, а сами они будут представлены один за другим, на последующих отдельных страницах. Преимущества такого отдельного расположение «рисунка», так же, как и для таблицы, связаны со значительным упрощением текстового редактирования статьи и с обеспечением большей наглядности представленных в ней данных. Такое улучшение наглядности обеспечивается, за счет возможности увеличить размеры рисунка в границах целой страницы, что позволяет гораздо отчетливее продемонстрировать мелкие, но важные его детали. Для этого, большие рисунки, прежде всего графики, желательно располагать в «альбомном формате», что обеспечивает более длинную ось абсцисс с большим числом делений (точностью) представления показателя-аргумента. Это может быть существенным для наглядной демонстрации изменений показателя-функции при незначительных изменениях показателя-аргумента. Предпочтительность расположения рисунка на отдельной странице обусловлена, еще и тем, что, согласно требованиям некоторых редакций, каждый рисунок должен быть представлен отдельным файлом, сделанным или в редакторе «Word», или в «Excel», который отсылается вместе с отдельным файлом текста статьи, где эти рисунки тоже представлены в соответствующих местах. Однако, если, из-за отдельно расположенных рисунков, общий объем статьи превышает редакторские ограничения, то придется рисунки располагать, непосредственно среди текста, что значительно усложнить редактирование, как текста, так и самого рисунка. Суть этой сложности и способы ее преодоления такие же, как и для таблицы, расположенной, непосредственно среди текста. Все рисунки, приведенные в статье, необходимо обязательно нумеровать, по мере описания в тексте представленных на них сведений (начиная с первого). Номер рисунка, как правило, соответствует его порядковому номеру среди всех рисунков, на которые ссылается автор при текстовом изложении научного материала.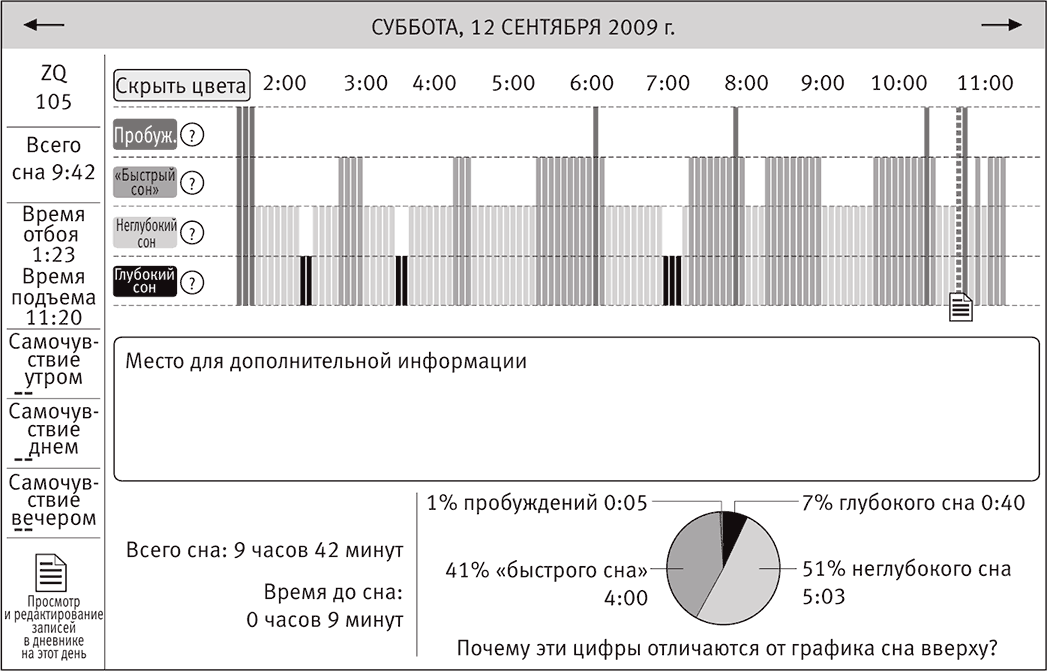 Но, поскольку их кол-во обычно регламентируется редакцией, то в рисуночном виде необходимо представлять, прежде всего, те сведения, которые подтверждают достижение научной цели исследования и решение поставленных научных задач, а также, наиболее характерные и необычные (впечатляющие) результаты. Это касается, в первую очередь, сведений представленных в главном и основном (ив других) промежуточных выводах, представленных в разделе статьи «Выводы». Впрочем, какие данные представлять в том или ином графическом виде, а какие только в тексте или в таблице, решает сам автор. Главное, чтобы графически представленные сведения были понятны читателю и легко им воспринимались, а также не дублировали выводы, сделанные на основании табличных данных. Общие правила оформления рисунка, его месторасположение на странице и особенности текста заголовка, надписей, подписей и т.п. приводятся в редакционных требованиях к его оформлению. В научной статье, ее «рисунки» целесообразнее всего применять тогда, когда нужно визуально убедительно продемонстрировать существенные количественные или качественные изменения важных показателей, которые имеют непосредственное отношение к решению научных задач и к достижению цели проведенного исследования. Причем, в случае качественных изменений изучаемого показателя, только изображение измененных его свойств является единственным информационным способом доказательства их объективного существования, тогда, как количественные изменения могут быть представлены и в табличном виде. Таким образом, решение о применении рисунка, а не таблицы, для демонстрации экспериментальных данных, зависит, в первую очередь, от возможности быть измеренными, т.е. являются ли они качественными или количественными. Причем, количественные значения, используемые для построения гистограммы или диаграммы, обычно представлены усредненными величинами и поэтому, статистически они характеризуются определенным разбросом первичных экспериментальных данных, в виде среднего квадратического отклонения - ±5. В то же время, для построения графиков зависимостей (взаимосвязей) между показателями могут использоваться, как усредненные, так и одноразово-измеренные точечные их значения. Визуально представляя усредненные данных на гистограмме, желательно показать их разброс в виде ±5. Ее нужно изображать вертикальным отрезком (вверх - +д, вниз - -д), проходящим через точку, соответствующую этому усредненному значению (верх столбика). Так же можно представить достоверность усредненных значений, используемых для построения графика. Для графика, построенного по одноразовым измерениям, проведенным в нескольких одинаковых экспериментах, достоверность можно подтвердить, наложив, в рамках одних и тех же координат, несколько полученных зависимостей одна на другую (т.е. провести их суперпозицию). Такой подход часто применяется в электрофизиологии при фотофиксации потенциала нервной клетки, вызванного раздражением нерва. Близость или совпадение наложенных графиков докажет повторяемость взаимосвязи и наоборот, а, следовательно, и степень ее достоверности. Кроме того, достоверность зависимости может быть рассчитана с помощью специальных статистических методов, в виде доверительной вероятности повторения события при определении ее уравнения. Для наглядной демонстрации количественных различий, которые свидетельствуют о сравнительном изменении одного и того же изучаемого показателя, обычно используют столбиковую гистограмму - диаграмму Ганта. При этом, нужно подчеркнуть, что хорошо видимое различия между столбиками сравниваемых средних значений (без изображения ±5) может и не служит убедительным аргументом в пользу того, что одно из них больше или меньше другого. Это объясняется тем, что такое отличие «средних арифметических» было обусловлено присутствием среди усредняемых значений выброса (или неожиданно большого, или маленького значения). Он, обычно является следствием воздействия неконтролируемого экспериментатором вероятностного фактора и свидетельствует о недостаточной методической чистоте эксперимента. Поэтому, для визуального доказательства достоверности количественных различий усредненных значений показателя (если это не сделано в тексте или в таблице), надо представить на гистограмме их средние квадратические отклонения. Для этого надо, ориентироваться на окончание отрезков, соответствующих величине «±8», проходящих через верхние точки сравниваемых столбиков. Демонстрируемые различия показателя являются объективно существующими (статистически достоверными) только в том случае, когда нижний конец отрезка (-8) большего значения находится выше верхнего конца отрезка (+8) меньшего значения (т. е. эти половинки отрезков с величинами д не перекрываются). Такое «не перекрытие» графически демонстрирует существование статистически достоверного различия между сравниваемыми среднестатистическими значениями и является основанием для их научной интерпретации. Если же никаких изменений не было зарегистрировано, или видимые различия (на основании перекрытия значений среднеквадратических отклонений - ±5) статистически недостоверны, или незначительны, хотя и достоверны, то гистограмму применять нецелесообразно. Вполне достаточно, просто упомянуть о таком факте в тексте, а при острой необходимости, сослаться на соответствующую таблицу. При построении гистограммы обязательно нужно подписывать названия осей (вертикальную и горизонтальную), а по отношению к вертикальной оси, еще и создать шкалу с делениями определенной размерности. Точность этих делений (частота нанесения отметок на вертикальную ось) должна позволять визуально определить величину отображенного свойства сравниваемых значений показателя. При этом, точность делений должна быть такой, чтобы визуально можно было легко определить самую маленькую величину различий между изображенными столбиками - усредненными значениями. Для круговой диаграммы такой специальной шкалы не существует, поэтому достаточно напечатать названия каждого сектора, соответствующего отображенному им свойству и его размерность (обычно, в процентах - %). И для гистограммы, и для диаграммы необходимо обеспечить четкое визуальное различие сравниваемых столбиков или секторов не только за счет разной высоты или площадей, но и с помощью их «раскраски». При этом, нежелательно использовать разные цвета, т.к. в журнальной статье, это не допускается редакционными правилами (все рисунки должны быть только черно-белыми). Используйте вместо цвета, разную штриховку, причем, для соседних столбиков и секторов, хорошо различимую (например, правая поперечная, а левая - косая или точечная). Обеспеченная таким способом «контрастность» восприятия должна быть тем выразительнее, чем меньше сравниваемые различия значений, находящиеся рядом (и справа, и слева) от его столбика. Выбранная черно-белая «текстура-штриховка», заполняющая внутреннее пространство столбика или сектора, не должен затруднять (маскировать) считывание расположенных в них надписей и цифр. Современные программные средства (например, Excel-2003) позволяют выбрать нужный «рисунок-заполнитель» из большого набора возможных вариантов при построении гистограмм и круговых диаграмм. При этом, не следует использовать объемное (трехмерное) изображение и другие «навороты», которыми располагает соответствующие компьютерные программы. Их неадекватное применение только, «смазывает» визуально воспринимаемый эффект существования различий. Трехмерное изображение целесообразнее применять только тогда, когда изучаемый сложный показатель (объект исследования) характеризуется тремя свойствами (показателями), которые измеряются (регистрируются) в эксперименте. Тогда, например, высота столбиковой гистограммы будет характеризовать величину одного свойства, ширина - другого, а глубина - третьего, но одного и того же исследуемого показателя (сложного объекта). Таким же образом можно использовать и сложную двумерную гистограмму (с высотой и шириной столбика) для отображения общей количественной характеристики сложного показателя, характеризующегося двумя разными свойствами (одно по высоте, другое по ширине), но, как правило, это не делается. Обычно же, с помощью стандартной столбиковой двухмерной (простой) гистограммы отображаю только одно свойство показателя, величина (интенсивность) которого соответствует высоте столбика, а его ширина одинаковая для всех. При этом, по вертикали пишется название этого свойства, его размерность и шкала измерения (с делениями и оцифровкой), а по горизонтали - только название показателя или его качественные особенности, или условия его регистрации. При использовании аббревиатуры названий этих условий и особенностей, они могут быть написаны и в пространстве соответствующего столбика, а не на горизонтальной оси гистограммы. В трехмерной и сложной двухмерной гистограмме, отражающей, соответственно, три и два свойства представленного показателя, такие пояснительные надписи придется сделать, соответственно, для трех и двух осей, а его название отдельно привести в заглавии рисунка. В том случае, когда необходимо продемонстрировать соотношение (например, процентное) представления разных качеств (свойств), характеризующих один и тот же объект, целесообразнее использовать круговую диаграмму. В ее изображении, круг является символом всего объекта (его обобщенного - цельного качества), а отдельные части круга (секторы) изображают качества тех составных свойств, которые определяют это общее качество сложного объекта. Чем больше площадь сектора, тем больший вклад соответствующего свойства (показателя) в общее качество и наоборот. Благодаря круговой диаграмме, лучше визуально воспринимается вклад каждого из простых составляющих показателей в общую характеристику всего изучаемого явления (сложного показателя). Для демонстрации тенденции изменения (а не величины различий) показателя во времени или под воздействием различной интенсивности одного и того же фактора, или/и для графического представления математической зависимости между показателями целесообразнее использовать графики. Благодаря графическому изображению отчетливее отслеживается тенденция-направленность, интенсивность и характер выявленных изменений или взаимосвязей. Для этого необходимо всегда подписывать обе оси координат графика (и ординат, и абсцисс) названиями соответствующих показателей или только единицами времени для оси абсцисс. Кроме того, обе эти оси должны иметь шкалу (деления с соответствующей оцифровкой), точность которой позволяет определить численные значения любой точки на графике. В первую очередь, это относится к экспериментально полученным точкам-значениям, на основании которых и построен график. Благодаря этому, упрощается визуальное обнаружение существования или отсутствия взаимосвязи между изучаемыми показателями, что может послужить основанием для дальнейшего ее уточнения специальными статистическими методами. При этом, следует, еще раз подчеркнуть, что выяснить, какой из этих двух взаимосвязанных показателей является аргументом, а какой функцией, нельзя никакими статистическими методами. Ни коэффициенты линейной, ни нелинейной корреляции, ни статистически обоснованное математическое уравнение зависимости, в принципе, не могут это сделать. Чтобы определить причинно-следственные связи между изучаемыми показателями, и таким способом подтвердить факт изменения одного из них, только под воздействием другого, необходимо провести целенаправленные эксперименты по выявлению, какой из них является функцией, а какой аргументом. Не целесообразно строить график при наличии меньше четырех экспериментально полученных или усредненных значений (точек) для каждого из рассмотренных показателей. Это объясняется тем, что по трем и менее точкам трудно определить достоверно существующую тенденцию изменения (особенно, нелинейную). Такие данные целесообразнее представить или текстом, или гистограммой (со сравниваемыми столбиками-значениями), которые достаточно хорошо отразят полученные изменения (не претендуя на тенденцию). И автору не нужно обсуждать их направленность, а достаточно ограничиться, только сравнительным анализом имеющихся количественных отличий (больше, меньше). Его результат можно представить, например, текстовым комментарием, что при такой-то величине одного показателя значение другого было таким-то, а при другой таким-то. Также, в статье не следует использовать график, если в эксперименте фиксируются изменения одного и того же показателя при индивидуальном воздействии разных экспериментальных факторов (условий). Для этого лучше, также использовать столбиковую гистограмму, где по горизонтали будут приведены названия этих разных факторов, а по вертикали свойство изучаемого показателя, величины которого соответствуют воздействию разных экспериментальных факторов. Хотя графики, гистограммы, диаграммы и строятся на основании количественных значений, приведенных в таблице, но они по своему информационному содержанию и целевому предназначению не должны дублировать текущие табличные выводы. Эти разновидности графического изображения целесообразно применять, прежде всего, по отношению к тем показателям, сравниваемые табличные значения которых или многочисленны, и/или визуально существенно отличаются между собой, и/или имеют достаточно отчетливую тенденцию изменения. Поэтому, об этих, экспериментально выявленных особенностях не следует упоминать в табличных выводах, а описывать их в тексте отдельно, как выводы, которые следуют из анализа соответствующего «рисунка». Учитывая более выразительное, по сравнению с таблицей, представление данных на «рисунках», желательно, чтобы «графические выводы», сформулированные в разделе статьи «Выводы», естественно следовали из простого визуального анализа соответствующего изображения. Информационное содержание этих выводов должно отражать или общую тенденцию изменения показателя, и/или отдельные ее особенности (направленность, интенсивность), и/или вид математической зависимости. Графические выводы способны более убедительно продемонстрировать результаты решения основных экспериментальных задач и факт достижение научной цели. При этом, их формулировки должны обязательно содержать термины и определения из названий и пояснительных подписей соответствующих «рисунков». Такая информационная преемственность является, еще одним редакторским аргументом в пользу размещения в статье каждого «рисунка» на отдельной странице. Это позволит нагляднее проиллюстрировать особенности полученных результатов, сформулированных в соответствующих окончательных выводах (в разделе статьи «Выводы»). Рассмотренные ранее виды графического представления в научной статье экспериментальных данных, касались тех из них, которые измерялись количественно (как минимум, в процентах). Но существуют первичные данные, которые не могут быть количественно измерены, в принципе, и имеют только визуально фиксируемые качественные признаки (свойства). Визуальное обнаружение таких «качественных данных» свидетельствует об их существовании (наличии), а, если они не обнаружены (например, на фотографии не видимы), то это означает их отсутствие. К «условно качественным данным», также можно отнести схемы, схематические изображения, фотографии и рисунки исследовательской аппаратуры, анкеты и т.п. Их наиболее часто применяют или в методических статьях, или в разделах «Методика» и «Обсуждение результатов» типовой научной статьи. Например, схема может демонстрировать последовательность логических процедур достижения научной цели или этапов исследования при обсуждении его результатов. Описание методики может содержать схематическое изображение компоновки рабочего места человека-оператора или расположения электродов на его теле для регистрации психофизиологических показателей. Образцы анкет и вопросников, также являются «условно качественными данными» и тоже могут быть представлены в методике статьи. Фотография («художественный рисунок»), свидетельствующая о появлении (существовании) конкретного видимого признака (свойства) изучаемого объекта, предназначена для визуального подтверждения его экспериментального происхождения. Кроме того, фотографию можно использовать для демонстрации особенностей экспериментальной аппаратуры, лицевой части прибора или пульта управления, рабочего места человека-оператора, внешнего вида и помехоустойчивости регистрации психофизиологических показателей и т.п. Другими словами, если необходимо продемонстрировать качественные особенности показателя (объекта), который не имеет количественного выражения, или что-либо, просто проиллюстрировать, то фотография и «художественный рисунок» являются единственным способом сделать это наиболее эффективно. Причем, в отношении изучаемого явления (показателя, его свойства), то фотография зафиксированной реальности или ее «художественный образ» (т.е., тщательная ее зарисовка) гораздо убедительнее докажет и/или покажет наличие соответствующего феномена. Только с их помощью и можно увидеть качественные свойства, которые были зарегистрированы, и доказать факт или их объективного существования (возникновения), или изменения - не изменения (в эксперименте), или наличие особенностей этих изменений. Фиксация с помощью фотокамеры или карандаша реально наблюдаемой действительности является единственным способом визуально отобразить любое изучаемое природное явление. Поэтому, фотография или «зарисованное изображение» в научной статье незаменимы, как одни из видов графического представления экспериментальных данных, если необходимо продемонстрировать их визуально-воспринимаемые качественные особенности. Наиболее целесообразно применять этот вид графического изображения для доказательства факта возникновения или исчезновения признака (свойства) с характерными «визуальными особенностями», до и после воздействия экспериментального фактора или изменения условий наблюдения. При оформлении любых «статейных рисунков», в том числе, «художественных рисунков» и фотографий, никогда не используйте разные цвета. Все рисунки в научной статье должны быть, только черно-белыми, согласно редакционным требованиям, иначе, она не будет ее рассмотрена для публикации. Если же качественное свойство характеризуется цветом (его изменением), то используйте штриховку с пояснением ее «цветового» значения, которое представлено или на самом изображении, или рядом с ним. Название «статейного рисунка» должно, как можно полнее характеризовать информационное содержание изображенных на нем материалов. Для этого оно должно включать в себя конкретные или обобщающие названия осей (вертикальной и горизонтальной) столбиковой гистограммы и графика (осей ординат и абсцисс), секторов круговой диаграммы и видимых качественных особенностей, представленных на фотографии или на «художественном рисунке». Формулировка любого рисуночного названия может содержать или названия конкретных изображенных показателей, или их обобщенную характеристику. Что касается осей, то их названия (название показателя или свойства) надо стараться писать полностью. И только, если они слишком длинное и/или многословное (длиннее оси, изображенной на рисунке), то приходится использовать аббревиатуру. Но тогда, ее обязательно надо расшифровать в границах этого рисунка, а также в тексте статьи при первой же ссылке на этот рисунок. Эту аббревиатуру необходимо включить в название рисунка, в скобках, после соответствующего текста-расшифровки или снизу, или сбоку от самого изображения (это удобно делать, например, если рисунок создается в «Excel»). Кроме того, использовать аббревиатуру приходиться в случае многострочных названий осей на гистограмме и на графике при их небольшой длине. Формулировка названия сути статейного рисунка зависит от его разновидности. Так, в названии гистограммы или диаграммы, в первую очередь, внимание читателя обращается на факт различия, а не на его величину. В названии графика констатируют наличие изменения, взаимосвязи показателей. Название фотографии, «художественного рисунка» отражает сам факт существования (появления) качественного признака-свойства. После названия статейного рисунка сообщаются названия отображенных показателей и условий их наблюдения. Например, график посвященных взаимосвязи между уровнем психофизиологической напряженностью пилота и вероятность летного происшествия, из-за человеческого фактора, может иметь следующую формулировку: «Взаимосвязь эргономической вероятности летного происшествия, из-за человеческого фактора (ЧФ), с психофизиологической напряженностью пилота». Относительно места печатания названия статейного рисунка, то не желательно это делать в поле изображения (созданного с помощью рисуночного мастера), а лучше напечатать его отдельно вне этого поля, как простой текст. Таким способом значительно упрощается редактирование, как самого изображения (прежде всего, его размеров), так и его названия по содержанию и длине. Для повышения информационной ценности рисунка, его описание в научной статье, желательно проводить по определенной схеме. Так, для гистограммы или диаграммы, в первую очередь, внимание читателя обращается на величину имеющихся количественных различий, а не на сам факт их существования. Для графика, констатируется наличие тенденции изменения и ее направленность или отсутствие однонаправленных количественных изменений. На основании фотографии, «художественного рисунка» демонстрируют сам факт существования (появления) изучаемого качественного признака-свойства. И только затем, обсуждается величина различий (для гистограммы или диаграммы), характер, интенсивность и условия изменения (для графика), видимые особенности выявленных признаков (для фотографии и «художественного рисунка»). После чего, анализируются ключевые данных (видимые детали), прежде всего, с точки зрения решения поставленных научных задач и достижения цели исследования. Для этого можно использовать сравнения, например, во (на) сколько раз больше - меньше, быстрее - медленнее, увеличивается-уменьшается, позитивная - негативная зависимость, прямая - обратная связь, присутствует - отсутствует, появляется-исчезает и т.п. В научной статье, после соответствующего текста, в круглых скобках указывается номер рисунка, сведения из которого были описаны, в виде рисуночного текущего вывода. При этом, не рекомендуется использовать выражения-указатели: «на рисунке....», «согласно рисунку» и т.п., чтобы не отвлекать читателя от авторского описания и анализа экспериментального материала. Вместо этого, после текста - рисуночного текущего вывода, просто, в круглых скобках укажите номер соответствующего рисунка, например, (Рис. 1). Каждый рисунок с соответствующим текстовым описанием - это, как минимум, графическое отображение наиболее значимых данных из одной таблицы, которые можно использовать для формирования одного, именно, рисуночного вывода. Такой вывод, в случае подтверждения факта решения конкретной научной задачи или достижения цели исследования, обязательно надо привести в разделе статьи «Выводы» или в конкретной или в обобщенной формулировке. При этом, его формулировка, непосредственно в тексте публикации должна отличиться от его формулировки в «Выводах» или детализацией, или конкретизацией, или интерпретацией (т.е. быть более объемной по тексту). Поэтому, при определении, какие результаты, и в каком графическом виде следует представлять, исходите из их информационной ценности для подтверждения факта достижения научной цели и/или решения задач, сформулированных в вашей статье. Другими словами, изображенные на одном рисунке данные должны свидетельствовать о решении, как минимум, одной научной задачи и/или о достижении научной цели проведенного исследования. Поэтому, надо стремиться к тому, чтобы количество рисунков, в рамках редакционных ограничений, соответствовало количеству основополагающих выводов. Те выводы, которые, непосредственно не связаны с решением научных задач и с достижением цели, могут быть приведены только в тесте, как текущие, по мере изложения экспериментального материала. Но те из них, которые логически доказывают факт решения этих задач и/или достижения научной цели, должны быть обязательно представлены в разделе статьи «Выводы». Применение рисунков разного вида для представления в научной публикации результатов проведенного исследования является очень эффективным наглядным способом доказательства факта успешного решении поставленных научных задач для достижения цели проведенного исследования. Приведенные советы студенту по графическому представлению в научной статье полученных результатов обеспечат достаточную их информативность и понятность для читателя, при минимуме затраченных усилий и времени.шаблоны для dle 11.2 Разница между графиками и диаграммами (Наука и природа) Графики против диаграмм Иногда информация, предназначенная для понимания, является слишком длинной и сложной. Чтобы сделать его интересным и понятным в захватывающей манере, используются различные визуальные представления. Графики и диаграммы являются двумя общими средствами визуального представления информации, которая либо носит повторяющийся характер, либо является слишком сложной. Есть сходства в этих методах, которые путают многих, чтобы относиться к ним как к подобным. Тем не менее, есть различия, которые будут выделены в этой статье. Диаграммы Мы слишком хорошо осведомлены об использовании диаграмм для объяснения информации и фактов, представленных в виде текста. Если вам нужно объяснить детали машины или принцип ее работы, становится трудно заставить человека понять концепцию только с помощью текста. Именно здесь в игру вступают диаграммы в виде эскизов. Точно так же диаграммы широко используются в биологии, где студенты должны узнать о различных частях тела и их функциях. Визуальное представление концептов с помощью диаграмм имеет больше шансов на сохранение в памяти студентов, чем представление их в виде текста. Диаграммы обращаются вправо с момента поступления ребенка в школу, так как даже алфавиты представлены ему в более интересной и привлекательной форме с помощью диаграмм. диаграммы Всякий раз, когда в наборе информации есть две переменные, лучше представлять информацию в виде графиков, поскольку это облегчает понимание данных. Например, если кто-то пытается показать, как цены на товары выросли во времени, простой линейный график был бы более эффективным и интересным способом, чем перевод всей этой информации в виде текста, который трудно запомнить, тогда как даже непрофессионал может увидеть, как цены выросли или снизились по отношению ко времени. Графики используют графическую бумагу, которая имеет точные квадраты и представляет информацию в точной форме, и читатель может увидеть влияние одной переменной на другую очень простым способом.. Разница между графиками и диаграммами • Все графики являются диаграммой, но не все диаграммы являются диаграммой. Это означает, что диаграмма является лишь подмножеством графа. • График представляет собой представление информации с использованием линий на двух или трех осях, таких как x, y и z, тогда как диаграмма представляет собой простое графическое представление о том, как вещь выглядит или как она работает. • Графики являются представлениями в масштабе, тогда как диаграммы не должны быть в масштабе • Диаграммы более привлекательны для взгляда, поэтому они используются в рекламе, тогда как графики предназначены для статистиков и исследователей.. • Значения среднего и медианы могут быть рассчитаны с помощью графиков, что невозможно с диаграммами • Графики рисуются на миллиметровой бумаге, тогда как диаграммы не нуждаются в миллиметровой бумаге • Для распределения частот используются только графики, и они не могут быть представлены через диаграммы Разница между графиками и диаграммами 16 июня 2011 г. Автор: Оливия Графики и диаграммы Иногда информация, которую хотят понять, бывает слишком длинной и сложной. Чтобы сделать его интересным и увлекательно понятным, используются разные визуальные представления. Графики и диаграммы - два распространенных средства визуального представления информации, которая либо повторяется по своей природе, либо слишком сложна. В этих методах есть сходство, которое многих сбивает с толку, считая их похожими.Однако есть отличия, о которых будет рассказано в этой статье. Диаграммы Мы слишком хорошо осведомлены об использовании диаграмм для объяснения информации и фактов, представленных в виде текста. Если вам нужно объяснить части машины или принцип ее работы, становится трудно объяснить концепцию только с помощью текста. Вот тут-то и вступают в игру схемы в виде набросков. Точно так же диаграммы широко используются в биологии, где учащимся приходится узнавать о различных частях тела и их функциях.Визуальное представление концепций с помощью диаграмм имеет больше шансов на сохранение в памяти учащихся, чем представление их в виде текста. К диаграммам прибегают уже с момента поступления ребенка в школу, так как даже алфавиты преподносятся ему в более интересной и привлекательной форме с помощью диаграмм. Графики Когда в наборе информации есть две переменные, лучше представить информацию с помощью графиков, так как это облегчает понимание данных.Например, если кто-то пытается показать, как цены на товары росли с течением времени, простой линейный график был бы более эффективным и интересным способом, чем помещать всю эту информацию в виде текста, который трудно запомнить, тогда как даже неспециалист может увидеть, как цены росли или падали со временем. В графиках используется миллиметровая бумага с точными квадратами и точным представлением информации, и читатель может очень просто увидеть влияние одной переменной на другую. Разница между графиками и диаграммами • Все графики представляют собой диаграммы, но не все диаграммы являются графиками. Это означает, что диаграмма - это только подмножество графа. • График - это представление информации с помощью линий на двух или трех осях, таких как x, y и z, тогда как диаграмма - это простое графическое представление того, как объект выглядит или как он работает. • Графики представляют собой масштабы, тогда как диаграммы не обязательно должны быть в масштабе • Диаграммы более привлекательны для просмотра, поэтому они используются в рекламе, тогда как диаграммы предназначены для статистиков и исследователей. • Значения среднего и медианного могут быть рассчитаны с помощью графиков, что невозможно с диаграммами • Графики нарисованы на миллиметровой бумаге, тогда как диаграммы не нуждаются в миллиметровой бумаге. • Для частотного распределения используются только графики и не могут быть представлены в виде диаграмм Диаграмма против диаграммы - в чем разница? Diagramnoun План, рисунок, набросок или набросок, чтобы показать, как что-то работает, или показать отношения между частями целого. «Электрические схемы показывают соединения устройств.»; Diagramnoun График или диаграмма. Chartnoun Карта, показывающая географию конкретного явления. Diagramnoun (теория категорий) Функтор из индексной категории в другую категорию. Объекты и морфизмы индексной категории не обязательно должны иметь какую-либо внутреннюю субстанцию, а скорее просто очерчивают соединительную структуру по крайней мере некоторой части содомена диаграммы.Если индексная категория - J, а область значений - C, то говорят, что диаграмма «имеет тип J в C». Chartnoun Карта навигатора. Diagramverb (переходный) Для представления или обозначения чего-либо с помощью диаграммы. Chartnoun Систематическое не описательное представление данных. Diagramnoun Рисунок или рисунок, сделанный для иллюстрации утверждения или облегчения демонстрации; план. Chartnoun Табличное представление данных; стол. Diagramnoun Любой простой рисунок, сделанный для математических или научных целей или для помощи в словесном объяснении, относящемся к нему; механический рисунок в отличие от художественного. Diagramverb Оформить в виде диаграммы. Диаграмма существительное рисунок, предназначенный для объяснения того, как что-то работает; чертеж, показывающий взаимосвязь между частями Chartnoun Запись диагноза пациента, инструкции по уходу и недавняя история болезни. «Я украдкой взглянул на его карту. Выглядит не очень хорошо. »; Diagramverb сделайте схематический или технический чертеж, показывающий, как все работает или как они устроены. Chartnoun Ранжированный список конкурентов по записанной музыке. «На этой неделе они снова на вершине хит-парадов»; Диаграмма существительное упрощенный рисунок, показывающий внешний вид, структуру или работу чего-либо; схематическое изображение «Схема гостиной»; Chartnoun Письменный акт; устав. Диаграмма существительное фигура, состоящая из линий, которая используется для иллюстрации определения или утверждения или для помощи в доказательстве предложения. Chartnoun (топология) Подпространство коллектора, используемое как часть атласа Diagramnoun графическое расписание для работы железнодорожных локомотивов и подвижного состава для предоставления желаемой услуги. Chartverb (переходный) Чтобы нарисовать диаграмму или карту. Diagramverb представляют (что-то) в графической форме «эксперимент изображен на четырнадцатой странице»; Chartverb (переходный) Чтобы нарисовать или вычислить (маршрут или план). «Давайте наметим, как мы собираемся добраться отсюда туда»; «Мы идем курсом к катастрофе, но не наметили ее»; Diagramverb планировать работу (локомотива или поезда) в соответствии с диаграммой. Chartverb (переходный) Для систематической записи. Диаграмма Диаграмма - это символическое представление информации с использованием методов визуализации. Диаграммы использовались с древних времен на стенах пещер, но стали более распространенными в эпоху Просвещения. Chartverb Чтобы появиться на диаграмме записи попаданий. «Песня в чартах 15 недель!»; «Группа впервые попала в чарты в 1994 году»; Chartnoun Лист бумаги, картона и т. П., На котором отображается информация, в особенности. когда информация представлена в виде таблицы; как, исторический график. Chartnoun Карта; особенно гидрографическая или морская карта; карта, на которой проецируется часть воды и земли, которую она окружает или которой она окружена, специально предназначенная для использования моряками; as, карты Обзора побережья США; карты английского Адмиралтейства. Chartnoun Письменный акт; устав. Chartverb Положить в график; для отображения; очертить; как, чтобы нанести на карту побережье. Chartnoun визуальное отображение информации Chartnoun карта, предназначенная для помощи в навигации по воздуху или морю Chartverb составьте карту; «нанесение на карту территории»; Chartverb план в деталях; «Буш намечает курс на уничтожение Саддама Хусейна»; Chartverb представить в виде графика; «диаграмма данных»; Chartnoun информационный лист в форме таблицы, графика или диаграммы «врач записал ее кровяное давление на диаграмме»; Chartnoun еженедельный список текущих популярных популярных рекордов «она возглавляла чарты в течение восьми недель»; Chartnoun географическая карта или план, особенно тот, который используется для навигации по морю или воздуху «карта побережья Англии»; Chartnoun круговая карта, показывающая положение планет в двенадцати домах во время чьего-либо рождения, из которой астрологи, как говорят, могут определить их характер или потенциал. Chartverb составить карту (области) «Кук нанес на карту побережья и воды Новой Зеландии»; Chartverb участок (курс) на карте «пилот обнаружил, что его судно движется по маршруту, которого он не наметил»; Chartverb зафиксировать прогресс или развитие «стихи показывают его падение в безумие»; «Крупный сериал, посвященный истории музыки кантри»; Chartverb (записи) продано достаточно копий, чтобы войти в музыкальные чарты на определенной позиции «запись, вероятно, займет около No.74 ’; Диаграмма Диаграмма - это графическое представление для визуализации данных, в котором. Диаграмма может представлять табличные числовые данные, функции или некоторые виды структуры качества и предоставлять различную информацию. «данные представлены символами, такими как столбцы на линейчатой диаграмме, линии на линейной диаграмме или срезы на круговой диаграмме»; Диаграмма или диаграмма - в чем разница? Альтернативные формы * диаграмма ( архаичный ) Существительное ( ru имя существительное ) План, рисунок, набросок или набросок, чтобы показать, как что-то работает, или показать отношения между частями целого. * {{quote-magazine, date = 2012-03 , автор = , title = Pixels or Perish , объем = 100, выпуск = 2, страница = 106 , журнал = цитата , пассаж = Рисунки и картинки - это больше, чем просто украшения в научном дискурсе. Наброски на доске, геологические карты, диаграмм молекулярной структуры, астрономические фотографии, изображения МРТ, множество разновидностей статистических диаграмм и графиков: эти графические устройства являются незаменимыми инструментами для представления доказательств, для объяснения теории, для рассказа истории.}} Электрические схемы На схемах показаны соединения устройств. График или диаграмма. (теория категорий) Функтор из индексной категории '' в другую категорию. Объекты и морфизмы индексной категории не обязательно должны иметь какую-либо внутреннюю субстанцию, а скорее просто очерчивают соединительную структуру по крайней мере некоторой части содомена диаграммы. Если индексная категория - «J», а домен - «C», то говорят, что диаграмма имеет тип «J» в «C ». Синонимы * (План или аналогичный, чтобы показать взаимосвязи или аналогичный ) схема Гипонимы * Смотрите также Производные термины * принципиальная электрическая схема * Диаграмма Исикавы * логическая схема * ( древовидная диаграмма ) * Диаграмма Венна Глагол Для представления или обозначения чего-либо с помощью диаграммы. Связанные термины * схематический * схематично ---- Английский Существительное ( ru имя существительное ) Карта. # Карта, иллюстрирующая географию конкретного явления. # Карта штурмана. Систематическое представление данных без повествования. # Табличное представление данных; стол. # * {{quote-magazine, date = 2012-03 , author =, volume = 100, issue = 2, page = 106 , журнал = , title = Pixels or Perish , пассаж = Рисунки и картинки - это больше, чем просто украшения в научном дискурсе. Наброски на доске, геологические карты, диаграммы молекулярной структуры, астрономические фотографии, изображения МРТ, множество разновидностей статистических диаграмм и графиков: эти графические устройства являются незаменимыми инструментами для представления доказательств, для объяснения теории, для рассказа истории.}} # Схема. # График. # * {{quote-magazine, date = 2013-11-30, volume = 409, issue = 8864, magazine = ( The Economist ), author = Paul Davis , title = Буквы: скажите как можно проще , пассаж = Поздравляем, вы смогли использовать фразу «преобладающий критерий» в таблице (« По вашим оценкам », 9 ноября). Была ли эта работа какоррафиофобного журналиста вызовом со стороны его коллег или просто примером глоссолалии?}} # Запись диагноза пациента, инструкции по уходу и недавний анамнез. # Ранжированный список конкурентов по записанной музыке. Документ письменный; устав. (топология) Подпространство многообразия, используемое как часть атласа Производные термины * карта предков * гистограмма * штурманская рубка * картографическая книга * нанесено на карту * таблица * chartjunk * безналичный * чартометр * штурманский зал * контрольная диаграмма * глазковая диаграмма * флипчарт * блок-схема * музыкальный чарт * организационная диаграмма * организационная структура * Диаграмма PERT * круговая диаграмма * психрометрическая диаграмма * таблица рекордов * таблица спагетти * звездная карта * пошаговая диаграмма * настенная диаграмма * карта погоды Глагол ( en глагол ) Чтобы нарисовать диаграмму или карту. Чтобы нарисовать или выяснить (маршрут или план). Давайте наметим , как мы собираемся добраться отсюда туда. Мы идем курсом к катастрофе, не имея на карте ее. Для систематической записи. (пластинки или исполнителя) Появиться в хит-параде. Песня попала в чарты за 15 недель! Первая группа попала в чарты в 1994 году. Производные термины * диаграмма * пересчитать Связанные термины * карта * картография * мультфильм * картуш * чартер * Чартист * Magna Carta Анаграммы * * ---- Графики и графики | 6 лучших отличий (с инфографикой) Различия между графиками и диаграммами Обычно графики и диаграммы в Excel очень похожи друг на друга, но они разные. Графики в основном представляют собой числовое представление данных, поскольку они показывают взаимосвязь изменения чисел с тем, как одно число влияет или изменяет другое, однако, диаграммы - это визуальное представление, в котором категории могут быть связаны друг с другом, а могут и не быть связаны друг с другом, а также то, как информация отображается на графиках и диаграммах, различается. «Все графики являются разновидностями графиков, но не все графики являются графиками». В заявлении очень хорошо резюмируются эти два аспекта и четко указывается, какой из них шире, а какой является подмножеством другого. Отображение данных значимым и четким образом с визуальным представлением значений, которое позволяет предполагаемому пользователю легко понять и проанализировать данные, не вдаваясь в подробные детали таких данных, является основной целью концепции использования графиков и диаграмм. Что такое график? Графики в основном ориентированы на необработанные данные и отображают тенденции, связанные с такими данными в течение долгого времени. График в основном двухмерный и показывает взаимосвязь между данными через линию, кривую и т. Д., Используя горизонтальную линию внизу (называемую осью X) и вертикальную линию вдоль стороны (называемую осью Y). Согласно Advanced English Dictionary, «График - это математическая диаграмма, показывающая взаимосвязь между двумя или более наборами чисел или измерений.«График позволяет пользователю легко представить значения в данных через визуальное представление. Пример базового графика показан ниже: Приведенный выше график является базовым графиком, который позволяет пользователю получить визуальное представление о том, что данные, нанесенные на его оси Y, имеют тенденцию к увеличению, которая отображается в годах на оси X. Есть два типа графиков - гистограммы и линейные графики. Вы можете свободно использовать это изображение на своем веб-сайте, в шаблонах и т. Д. Пожалуйста, предоставьте нам ссылку с указанием авторства Ссылка на статью с гиперссылкой Например: Источник: Графики против диаграмм (wallstreetmojo.com) Что такое диаграмма? Диаграмма - это тип представления больших наборов данных, который позволяет пользователю лучше понимать их, а также помогает в предсказании существующих данных и прогнозировании будущих данных на основе существующего шаблона данных. Диаграмма может иметь форму диаграммы, изображения или графика. Наборы данных можно преобразовать в осмысленное отображение информации с помощью диаграмм. Пример простой диаграммы показан ниже: Диаграмма выше представляет собой простую диаграмму столбцов. Диаграмма столбцов используется для представления данных в вертикальных столбцах.Высота столбца представляет собой значение для определенного ряда данных на диаграмме, столбчатая диаграмма представляет собой сравнение в виде столбца слева направо. Подробнее, отражающее продажи продуктов мороженого компанией в разные дни неделя. С первого взгляда пользователь может определить самый высокий и самый низкий день продаж в неделю. Диаграммы могут упростить данные, а также распределить их по категориям в простые для понимания и анализа форматы и найти свое чрезмерное использование в бизнесе, где данные представлены с использованием различных типов диаграмм. Существуют типы диаграмм - вертикальные гистограммы, исторические гистограммы, гистограммы с накоплением, гистограмма, круговая диаграмма в Excel. Круговая диаграмма представляет собой круговую диаграмму Excel, представляющую визуализацию данных в круговом формате. В этой круговой диаграмме каждая категория данных имеет свою часть, и все категории составляют единые круговые данные. Подробнее, Линейная диаграмма и диаграммы с областями в Excel Диаграмма с областями в Excel представляет собой линейную диаграмму, которая показывает влияние и изменения в различных рядах данных с течением времени, разделив их линиями и представив их разными цветами.Для создания этого графика используется линейная диаграмма. Читать дальше. Список не является исчерпывающим, есть множество других популярных типов диаграмм; однако выбор диаграммы для представления данных является обременительной задачей, которую должен решить пользователь. Графики и диаграммы Инфографика Здесь мы предлагаем вам 6 основных отличий между графиками и графиками Вы можете свободно использовать это изображение на своем веб-сайте, в шаблонах и т. Д. Пожалуйста, предоставьте нам ссылку с указанием авторства Ссылка на статью с гиперссылкой Например: Источник: Графики против диаграмм (wallstreetmojo.com) Ключевые отличия Диаграммы представляют собой большой набор информации в виде графиков, диаграмм или таблиц, тогда как график показывает математическую взаимосвязь между различными наборами данных. Таким образом, график - это тип диаграммы, но не все. Фактически, Graph - это разновидность подгруппы Chart. Диаграмма, напротив, может принимать форму графика или какой-либо другой диаграммы или изображения. Диаграммы могут представлять данные всех типов в виде визуально привлекательного шаблона; однако в случае Graph более идеальным вариантом будет иметь те данные, которые отображают любой тип тенденции или взаимосвязи между переменной, нанесенной на две оси, чтобы лучше понять предполагаемого пользователя. Диаграммы удобны в тех случаях, когда данные должны быть хорошо распределены по категориям (например, по региону, возрасту и т. Д.) Или усреднены, что дополнительно упрощает отображение. Напротив, графики больше предназначены для выявления тенденций или закономерностей в наборах данных. Графики и диаграммы Сравнительная таблица Основа Графики Графики Значение График - это тип диаграммы, которая используется для отображения математической взаимосвязи между различными наборами данных. по горизонтали (ось X) и вертикали (ось Y). Диаграмма представляет информацию, которая может быть в форме диаграммы, таблицы или самого графика, и включает в себя различные методы для представления большой информации. Подмножество Все графики являются диаграммами. Это означает, что независимо от того, какой тип графика используется для отображения данных, он всегда будет типом подмножества графиков. Все диаграммы не являются графиками. Это означает, что могут быть и другие типы диаграмм, кроме диаграмм. Анализируемые данные Графики также могут использоваться для необработанных данных и обеспечивают визуальное представление тенденций и изменений в данных за определенный период времени. Идеально подходит для тех форм данных, которые можно легко структурировать или разделить по категориям на небольшие подмножества простых и легко понятных фигур. Использование Графики находят свое более широкое применение в Анализе, используя как необработанные данные, так и точные числа, и, как таковые, показывают точные числовые значения, нанесенные на его оси. Диаграммы широко используются в бизнес-презентациях и при демонстрации результатов опросов. Примеры круговых диаграмм - самые популярные, используемые в бизнес-презентациях. Анализ тенденций График - идеальный выбор для тех данных, которые отображают некую тенденцию или связь между переменными, изображенными на графике. Диаграммы также могут использоваться в тех случаях, когда отображаемые данные не отображают какой-либо тренд или взаимосвязь. Общие типы Линейный график Линейные графики / диаграммы в Excel - это визуальные элементы для отслеживания тенденций или отображения изменений за определенный период, и они очень полезны для прогнозирования данных.Они могут включать 1 строку для одного набора данных или несколько строк для сравнения различных наборов данных. читать далее Линейные графики / диаграммы в Excel - это визуальные элементы для отслеживания тенденций или отображения изменений за определенный период, и они очень полезны для прогнозирования данных. Они могут включать 1 строку для одного набора данных или несколько строк для сравнения различных наборов данных. читать далее Линейные графики / диаграммы в Excel - это визуальные элементы для отслеживания тенденций или отображения изменений за определенный период, и они очень полезны для прогнозирования данных.Они могут включать 1 строку для одного набора данных или несколько строк для сравнения различных наборов данных. подробнее и гистограмма. Популярные типы диаграмм: круговая диаграмма, гистограмма, вертикальная и историческая столбчатая диаграмма. Столбчатые диаграммы в Excel полезны для представления отдельных данных на горизонтальной полосе с категориями, отображаемыми на оси Y, и значениями на оси X. Для создания гистограммы нам понадобятся как минимум две независимые и зависимые переменные. Подробнее. Заключение Charts and Graphs часто используются при представлении данных, как сырых, так и точных, и доставляются с точки зрения того, чтобы сделать их визуально привлекательными и легкими для понимания предполагаемыми пользователями.Очень часто неправильно понимать их из-за очень тонкой линии различий между ними. Это мощные инструменты визуального представления для сжатия больших наборов данных в небольшие капсулы визуально привлекательных наборов информации, которые могут принимать форму различных типов диаграмм и графиков. Рекомендуемые статьи Это был справочник по диаграммам и графикам. Здесь мы также обсуждаем основные различия между диаграммами и графиками, а также инфографику и сравнительную таблицу.Вы также можете ознакомиться со следующими статьями - Пакет All in One Excel VBA (35 курсов с проектами) 35+ курсов 120+ часов Полный пожизненный доступ Свидетельство о завершении ПОДРОБНЕЕ >> 【решено】 Разница между графиком и графиком В чем основное различие между диаграммой и графиком? Диаграммы представляют большой набор информации в виде графиков, , диаграмм или в форме таблиц , тогда как график показывает математическую взаимосвязь между различными наборами данных.Таким образом, график является разновидностью диаграммы , но не полностью. Фактически, График является разновидностью подгруппы Графика . Что подразумевается под графиками и диаграммами? Что такое графиков и диаграмм? Графики и диаграммы - это визуальные элементы, которые показывают взаимосвязи между данными и предназначены для отображения данных таким образом, чтобы их было легко понять и запомнить. Люди часто используют графиков и диаграмм, чтобы продемонстрировать тенденции, закономерности и взаимосвязи между наборами данных. Чем гистограмма отличается от диаграммы? Разница между столбчатой диаграммой и столбчатой диаграммой Диаграммы Bar и столбец отображают данные с использованием прямоугольных столбцов , где длина столбца пропорциональна значению данных. Обе диаграммы используются для сравнения двух или более значений. Однако разница заключается в их ориентации. Что такое гистограмма, поясняющая на примере? Гистограмма - это график с прямоугольными столбцами .График обычно сравнивает разные категории. Для примера , если у вас есть два дома и требуются бюджеты для каждого, вы можете нанести из них на одну ось x с сгруппированной столбчатой диаграммой , используя разные цвета для представления каждого дома. См. Типы гистограмм ниже. Когда не следует использовать гистограмму? Не используйте гистограмму для сравнения элементов, требующих разных масштабов. Потому что это усложнит ваше сообщение.Вам также следует избегать использования гистограмм для отображения процентов, которые в сумме составляют целое, если они не разбиты по времени. Потому что это будет… Для чего лучше всего использовать гистограмму? Гистограммы - это , используемые для сравнения данных между разными группами или отслеживания изменений во времени. Однако при попытке измерить изменение с течением времени гистограмм являются лучшими , когда изменения больше. Чем полезна гистограмма? Гистограммы - это эффективный способ сравнения элементов между различными группами. Гистограммы - чрезвычайно эффективный визуальный элемент для использования в презентациях и отчетах. Они популярны, потому что позволяют читателю распознавать закономерности или тенденции гораздо легче, чем смотреть на таблицу числовых данных. Как выбрать правильный график? Линия , график показывает тенденции или прогресс во времени и может использоваться для отображения многих различных категорий данных. Дизайн Лучшие практики для линий Графики : Используйте только сплошные линии. Не наносите более четырех линий, чтобы не отвлекать внимание. Используйте правую высоту , чтобы линии занимали примерно 2/3 высоты оси y. Какие бывают 4 типа графиков? Есть несколько различных типов диаграмм и графиков . Наиболее распространенными из четырех являются, вероятно, линейные графики , столбчатые графики и гистограммы, круговые диаграммы и декартовы графики . Какой категории графиков вам следует избегать? Ответ. 1) Круговые диаграммы: круговые диаграммы представляют собой набор пропорциональных элементов, и всегда невозможно собрать какие-либо достоверные данные из результатов. Какой тип диаграммы подходит больше всего? Тип графика, который лучше всего использовать для отображения трендов, - Линейный график . Линейная диаграмма - один из наиболее часто используемых типов диаграмм, обычно используемый для отображения тенденций за определенный период времени.Он особенно используется для изображения изменений, происходящих с течением времени. Что делает диаграмму хорошей? Используйте соответствующие диаграммы , включая горизонтальные гистограммы. Используйте полную ось. Будьте проще, особенно с анимацией, и сделает уверенным с помощью теста на косоглазие. Используйте цвет для контраста и выделения данных. Какая диаграмма лучше всего подходит для относительного сравнения? Мы, как читатели, особенно хорошо умеем сравнивать длину столбцов на гистограмме (в отличие от сегментов круговой диаграммы , например), делая столбцов и столбчатых диаграмм лучшими диаграммами. для сравнения.По большей части, столбчатые диаграммы , и столбчатые диаграммы, могут использоваться как взаимозаменяемые. Какая диаграмма лучше всего подходит для сравнения? Гистограммы подходят для сравнений , а линейные диаграммы на лучше для трендов. Диаграммы рассеяния хороши для отношений и распределений, но круговые диаграммы следует использовать только для простых композиций - никогда для сравнения или распределений. Как вы показываете ранг графика? Используйте гистограммы, чтобы отображать данные , которые занимают рангов в возрастающем или убывающем порядке.Следует использовать турники. Столбчатая диаграмма всегда должна быть с рейтингом по значению, если нет естественного порядка данных (например, возраста или времени). Какой тип диаграммы лучше всего подходит для одновременного сравнения нескольких элементов? Линия Диаграмма : Линия диаграммы - это один из наиболее часто используемых типов диаграмм, обычно используемых для отображения тенденций за период времени. Если вам нужно, чтобы график менялся с течением времени, рассмотрите возможность использования линии на графике .Столбец Диаграмма : Столбец диаграмм обычно используется для сравнения нескольких элементов в определенном диапазоне значений . Какой тип диаграммы используется для отображения процентов? Одним из наиболее распространенных и узнаваемых способов визуализации процентов является круговая диаграмма , разновидностью которой являются кольцевые диаграммы. Сложенные столбцы графиков - еще один способ показать процентов . Как вы читаете графики и диаграммы? Чтобы интерпретировать график или график , прочтите заголовок, посмотрите на ключ, прочтите метки.Затем изучите график , чтобы понять, что он показывает. Прочтите заголовок диаграммы или диаграммы . Название сообщает, какая информация отображается. Какие 3 основных типа графиков? В этом курсе используются три типа графиков : линейные графики , круговые графики и столбчатые графики . Как вы используете графики? Разница между таблицей и диаграммой Таблица и диаграмма Таблица - это средство отображения данных или информации в строках и столбцах.Строки также называются записью или вектором, столбцы также называются параметрами, полями или атрибутами. Точка пересечения столбца и строки называется ячейкой. Таблица используется в исследованиях, анализе данных и коммуникации, и ее можно увидеть на различных носителях, от знаков до заметок в печати, в компьютерном программном обеспечении и в некоторых других местах. Он используется для отслеживания информации с точки зрения количества и чисел, а также имен, адресов и других деталей. Таблицы могут быть простыми, состоящими всего из нескольких столбцов и строк, или многомерными, состоящими из упорядоченных иерархий.Примером многомерной таблицы является таблица умножения. Таблицы используются в: Публикация - пример - таблица содержания Математика - пример - таблица умножения Естественные науки - пример - периодическая таблица Информационные технологии - пример - тот, который поддерживается программными приложениями, такими как программное обеспечение для обработки текстов и презентаций. Диаграмма, с другой стороны, представляет собой графическое отображение информации, в котором информация проиллюстрирована символами, такими как столбцы, линии или срезы.Он используется для определения взаимосвязи между большим количеством данных и их частями и упрощает чтение и понимание. Тексты редко используются в диаграммах; они в основном используются в заголовках, которые появляются над диаграммой и описывают данные, на которые имеется ссылка в диаграмме. Данные отображаются по горизонтальной (x) или вертикальной (y) оси, каждая из которых состоит из шкалы. Диаграмма также состоит из основной или вспомогательной сетки линий. Для данных, содержащих несколько переменных, диаграмма должна иметь легенду, в которой перечислены переменные в диаграмме для облегчения идентификации. Графики бывают нескольких типов: Общие диаграммы: гистограмма, линейчатая диаграмма, круговая диаграмма, линейная диаграмма, временная диаграмма, организационная диаграмма, древовидная диаграмма, блок-схема, диаграмма с областями, картограмма и диаграмма родословных. Менее распространенные диаграммы: пузырьковая диаграмма, диаграмма полярных областей, радарная диаграмма, диаграмма водопада и древовидная карта. Графики для конкретных областей: график открытия-максимума-минимума-закрытия, свечной график, график Каги и спарклайн. Хорошо известные диаграммы: диаграмма Нолана, диаграмма Ганта, диаграмма PERT и диаграмма Смита. Другие диаграммы: контрольная карта, натальная карта, номограмма, беговая диаграмма, структурная диаграмма и ленточная диаграмма. Резюме: 1. Таблица - это представление данных или информации в строках и столбцах, а диаграмма - это графическое представление данных в виде символов, таких как столбцы, линии и срезы. 2. Таблица может быть простой или многомерной. Хотя существует несколько типов диаграмм, наиболее распространенными являются круговые диаграммы, гистограммы и линейные диаграммы. 3. Тексты редко используются в диаграммах, в то время как они часто используются в таблицах. 4. Диаграмма используется для понимания большого количества данных и их компонентов, в то время как таблица используется для отслеживания такой информации, как количество, номера, имена, адреса и другие детали. : Если вам понравилась эта статья или наш сайт. Пожалуйста, расскажите об этом. Поделитесь им с друзьями / семьей. Cite APA 7 M, E. (2011, 6 сентября). Разница между таблицей и диаграммой. Разница между похожими терминами и объектами.http://www.differencebetween.net/science/mat Mathematics-statistics/difference-between-table-and-chart/. ОМС 8 М, Емельда. «Разница между таблицей и диаграммой». Разница между похожими терминами и объектами, 6 сентября 2011 г., http://www.differencebetween.net/science/mat Mathematics-statistics/difference-between-table-and-chart/. Столбиковая диаграмма - узнайте больше о столбчатых диаграммах и столбчатых диаграммах Что такое гистограмма, используемая для Гистограмма (также известная как гистограмма или гистограмма) - это визуальный инструмент, который использует столбцы для сравнения данных между категориями.Гистограмма может располагаться горизонтально или вертикально. Важно знать, что чем длиннее полоса, тем больше ее значение. Гистограммы состоят из двух осей. На вертикальной гистограмме, как показано выше, горизонтальная ось (или ось x) показывает категории данных. В этом примере это годы. Вертикальная ось (или ось Y) - это масштаб. Цветные полосы - это ряд данных. Гистограммы имеют три ключевых атрибута: Гистограмма позволяет легко сравнивать наборы данных между разными группами. График представляет категории по одной оси и дискретное значение по другой. Цель состоит в том, чтобы показать взаимосвязь между двумя осями. Гистограммы также могут отображать большие изменения данных с течением времени. Столбиковая диаграмма и линейная диаграмма Гистограммы отображают данные аналогично линейным графикам. Линейные графики полезны для отображения небольших изменений тенденции во времени. Гистограммы лучше подходят для сравнения больших изменений или различий в данных между группами. Когда использовать гистограмму Гистограммы - это эффективный способ сравнения элементов между разными группами. Эта гистограмма показывает сравнение чисел на квартальной основе за четырехлетний период времени. Пользователи этой диаграммы могут сравнивать данные по кварталам на основе годовой тенденции, а также видеть, как годовые продажи распределяются в течение каждого года. Гистограммы - чрезвычайно эффективный визуальный элемент для использования в презентациях и отчетах. Они популярны, потому что позволяют читателю распознавать закономерности или тенденции гораздо легче, чем смотреть на таблицу числовых данных. Типы гистограмм При визуальном представлении данных следует учитывать несколько различных стилей гистограмм. Вертикальная гистограмма Самый распространенный тип гистограммы - это вертикальная гистограмма. Это очень полезно при представлении ряда данных с течением времени. Одним из недостатков вертикальных гистограмм является то, что они не оставляют много места в нижней части диаграммы, если требуются длинные метки. Горизонтальная гистограмма Преобразование вертикальных данных в горизонтальную гистограмму решает эту проблему.По вертикальной оси достаточно места для длинной метки, как показано ниже. Гистограмма с накоплением Гистограмма с накоплением - это визуальный элемент, который может передавать большой объем информации. Убедитесь, что вы выбрали тип графика, который наилучшим образом представляет данные, которые вы хотите выделить. Как создать гистограмму Первый шаг - убедиться, что данные правильно отформатированы для гистограммы. На вкладке Insert в SmartDraw щелкните Graph и выберите тип Bar Graph.. Выберите файл данных для импорта, и SmartDraw автоматически сгенерирует гистограмму. После импорта вы можете легко изменить заголовок, размещение легенды и даже быстро изменить тип графика с помощью параметров Edit Graph или просто дважды щелкните импортированную диаграмму.

Основа сравнения графиков с графиками	диаграммы	Графики
Основное определение	График представляет собой вид диаграммы, которая представляет собой систему взаимосвязей или связей между двумя или более вещами несколькими отличительными линиями, точками, полосами и т. Д.	Диаграмма — это вид графического представления данных, в котором «данные, которые представлены символами, такими как линии на линейной диаграмме, столбцы на гистограмме или срезы на круговой диаграмме».
Представление	Графики покажут математические связи или взаимосвязь между наборами данных.	Графики будут представлять информацию или данные в виде диаграмм, графиков или таблиц.
Они такие же?	Все виды графиков являются диаграммами; следовательно, графики являются одним из видов диаграмм.	Все виды графиков не являются графиками.
Сфера	Графики также предоставляют визуальную форму, используя один из этих методов (то есть большую группу диаграмм), представляя данные в визуализированном формате.	Диаграммы — это большая группа методов, которые используются для представления данных или информации.
Что они делают?	Графики сделают фотографии из числовых данных или числовой информации.	Диаграммы, которые используются в диаграммах, могут показать последовательные события, такие как история рекомендаций правительства США по питанию или цикл горных пород.
Их типы	Круговые диаграммы, гистограммы, линейные графики и т. Д. Являются типами графиков и используются для различных целей.	Как указывалось ранее, графики являются подмножеством диаграмм, и, следовательно, диаграммы не имеют своего собственного типа, но, тем не менее, существуют примеры диаграмм, например, использование карт для включения статистики вождения в нетрезвом виде или местоположений вулканов и землетрясений.

	Таблица	Диаграмма
Представление данных	Числа и текст в строках и столбцах	Графическое представление, включая линии, полосы и круги.
Характеристики	Текст, цифры, легче сравнивать данные, представляет периодическую и изменчивую информацию, простую для понимания	большое разнообразие, графика, мало текста, картинки, легче для понимания, визуальный характер
Когда использовать	Чтобы найти или сравнить отдельные значения, чтобы показать точные значения, когда задействованы несколько единиц измерения.	Чтобы передать сообщение, которое содержится в форме данных, выявить взаимосвязь между многими значениями.
Типы	Простой стол, многомерный стол, широкие и узкие столы	Гистограмма, линейчатая диаграмма, линейная диаграмма, круговая диаграмма, временная диаграмма, организационная диаграмма, древовидная диаграмма, блок-схема, картограмма (карта), родословная диаграмма (семейное древо), пузырьковая диаграмма, потоковая диаграмма, диаграмма каги, диаграмма рассеяния и т. Д.
Используется в	Издательство, Математика, Естественные науки, Информационные технологии — разработка приложений и программного обеспечения.	Математика, Естественные науки, Информационные технологии

Основа	Графики	Графики
Значение	График - это тип диаграммы, которая используется для отображения математической взаимосвязи между различными наборами данных. по горизонтали (ось X) и вертикали (ось Y).	Диаграмма представляет информацию, которая может быть в форме диаграммы, таблицы или самого графика, и включает в себя различные методы для представления большой информации.
Подмножество	Все графики являются диаграммами. Это означает, что независимо от того, какой тип графика используется для отображения данных, он всегда будет типом подмножества графиков.	Все диаграммы не являются графиками. Это означает, что могут быть и другие типы диаграмм, кроме диаграмм.
Анализируемые данные	Графики также могут использоваться для необработанных данных и обеспечивают визуальное представление тенденций и изменений в данных за определенный период времени.	Идеально подходит для тех форм данных, которые можно легко структурировать или разделить по категориям на небольшие подмножества простых и легко понятных фигур.
Использование	Графики находят свое более широкое применение в Анализе, используя как необработанные данные, так и точные числа, и, как таковые, показывают точные числовые значения, нанесенные на его оси.	Диаграммы широко используются в бизнес-презентациях и при демонстрации результатов опросов. Примеры круговых диаграмм - самые популярные, используемые в бизнес-презентациях.
Анализ тенденций	График - идеальный выбор для тех данных, которые отображают некую тенденцию или связь между переменными, изображенными на графике.	Диаграммы также могут использоваться в тех случаях, когда отображаемые данные не отображают какой-либо тренд или взаимосвязь.
Общие типы	Линейный график Линейные графики / диаграммы в Excel - это визуальные элементы для отслеживания тенденций или отображения изменений за определенный период, и они очень полезны для прогнозирования данных.Они могут включать 1 строку для одного набора данных или несколько строк для сравнения различных наборов данных. читать далее Линейные графики / диаграммы в Excel - это визуальные элементы для отслеживания тенденций или отображения изменений за определенный период, и они очень полезны для прогнозирования данных. Они могут включать 1 строку для одного набора данных или несколько строк для сравнения различных наборов данных. читать далее Линейные графики / диаграммы в Excel - это визуальные элементы для отслеживания тенденций или отображения изменений за определенный период, и они очень полезны для прогнозирования данных.Они могут включать 1 строку для одного набора данных или несколько строк для сравнения различных наборов данных. подробнее и гистограмма.	Популярные типы диаграмм: круговая диаграмма, гистограмма, вертикальная и историческая столбчатая диаграмма. Столбчатые диаграммы в Excel полезны для представления отдельных данных на горизонтальной полосе с категориями, отображаемыми на оси Y, и значениями на оси X. Для создания гистограммы нам понадобятся как минимум две независимые и зависимые переменные. Подробнее.

Графики против диаграмм | Лучшие 6 отличий для изучения (с инфографикой)

Разница между графиками и графиками

Сравнение лицом к лицу между графиками и диаграммами (инфографика)

Ключевые отличия графиков от диаграмм

Сравнительная таблица графиков и графиков

Вывод — графики против диаграмм

Рекомендуемые статьи

Представление данных в виде точечной диаграммы или графика

Графические методы анализа данных

Разница между таблицей и графиком

Глава 6 Продвинутая графика | Визуализация и анализ географических данных на языке R

Предварительные требования

Загрузка данных Евростата

Загрузка данных Soil Data Access

Базовый шаблон ggplot

Геометрические типы и преобразования

Графические переменные и группировки

Системы координат

Названия осей и легенды

Разметка осей

Подписи и аннотации

Фасеты

Темы

Краткий обзор

Контрольные вопросы и упражнения

Вопросы

Упражнения

Рисунки, графики, диаграммы, схемы в работах студентов

Разница между графиками и диаграммами (Наука и природа)

Разница между графиками и диаграммами

против диаграммы - в чем разница?

Диаграмма или диаграмма - в чем разница?

Альтернативные формы

Существительное

Синонимы

Гипонимы

Производные термины

Глагол

Связанные термины

Английский

Существительное

Производные термины

Глагол

Производные термины

Связанные термины

Анаграммы

Графики и графики | 6 лучших отличий (с инфографикой)

Различия между графиками и диаграммами

Что такое график?

Что такое диаграмма?

Графики и диаграммы Инфографика

Ключевые отличия

Графики и диаграммы Сравнительная таблица

Заключение

Рекомендуемые статьи

Добавить комментарий Отменить ответ

Рубрики

`Добавить комментарий Отменить ответ`

`Рубрики`