Как вписать круг в квадрат: Please Wait… | Cloudflare

Онлайн калькулятор длины стороны вписанного в круг квадрата. Как узнать длину стороны вписанного в круг квадрата.

При помощи нашего калькулятора вы легко сможете узнать длину стороны вписанного в круг квадрата.

Для того что бы найти длину стороны вписанного в круг квадрата, нам необходимо узнать длину ребра этого квадрата. Для этого нам необходимо разделить квадрат по диагонали на два равнобедренных треугольника, при этом основание у этих треугольников будет равно диаметру круга.

Следующим действиям мы должны определиться с известной нам величиной круга в которую вписан квадрат, а именно нам должна быть известна:

1. либо площадь круга, обозначаемая буквой S,
2. либо периметр круга, обозначаемый буквой P,
3. либо радиус круга, обозначаемый буквой R,
4. либо диаметр круга, обозначаемый буквой D.

Начнем по порядку, мы имеем равнобедренный прямоугольный треугольник и для того, что бы узнать длину его ребер нам необходимо воспользоваться теоремой Пифагора исходя из которой

c² = 2a²,
Таким образом

a = √c²/2

Теперь для того что бы найти длину ребра треугольника (которое равно стороне нашего квадрата) нам необходимо узнать длину основания треугольника, которое равно диаметру круга

D = c

1. Если нам известна площадь круга в который вписан квадрат то для нахождения диаметра нам необходимо воспользоваться следующей формулой:

D=2√S/π

2. Если нам известна длина круга в который вписан квадрат то для нахождения диаметра нам необходимо воспользоваться следующей формулой:

D=P/π

3. Если нам известен радиус круга в который вписан квадрат то для нахождения диаметра нам необходимо воспользоваться следующей формулой:

D=2R

Соответственно если мы знаем диаметр круга который равен основанию треугольника полученного путем разделения квадрата на две части по диагонали,

c=D

мы можем узнать длину сторон квадрата используя теорему Пифагора

a = √c²/2

Как начертить квадрат в окружности

Построе́ния с по́мощью ци́ркуля и лине́йки — раздел евклидовой геометрии, известный с античных времён.

В задачах на построение циркуль и линейка предполагаются идеальными инструментами, в частности:

• Линейка не имеет делений и имеет сторону бесконечной длины, но только одну.
• Циркуль может иметь какой угодно большой или малый раствор (то есть может чертить окружность произвольного радиуса).

Содержание

Примеры [ править | править код ]

Задача на бисекцию. С помощью циркуля и линейки разбить данный отрезок AB на две равные части. Одно из решений показано на рисунке:

• Циркулем проводим окружности с центром в точках A и B радиусом AB.
• Находим точки пересечения P и Q двух построенных окружностей (дуг).
• По линейке проводим отрезок или линию, проходящую через точки P и Q.
• Находим искомую середину отрезка AB — точку пересечения AB и PQ.

Формальное определение [ править | править код ]

В задачах на построение рассматривается множество следующих объектов: все точки плоскости, все прямые плоскости и все окружности плоскости. В условиях задачи изначально задается (считается построенными) некоторое множество объектов. К множеству построенных объектов разрешается добавлять (строить):

1. произвольную точку;
2. произвольную точку на заданной прямой;
3. произвольную точку на заданной окружности;
4. точку пересечения двух заданных прямых;
5. точки пересечения/касания заданной прямой и заданной окружности;
6. точки пересечения/касания двух заданных окружностей;
7. произвольную прямую, проходящую через заданную точку;
8. прямую, проходящую через две заданные точки;
9. произвольную окружность с центром в заданной точке;
10. произвольную окружность с радиусом, равным расстоянию между двумя заданными точками;
11. окружность с центром в заданной точке и с радиусом, равным расстоянию между двумя заданными точками.

Требуется с помощью конечного количества этих операций построить другое множество объектов, находящееся в заданном соотношении с исходным множеством.

Решение задачи на построение содержит в себе три существенные части:

1. Описание способа построения заданного множества.
2. Доказательство того, что множество, построенное описанным способом, действительно находится в заданном соотношении с исходным множеством. Обычно доказательство построения производится как обычное доказательство теоремы, опирающееся на аксиомы и другие доказанные теоремы.
3. Анализ описанного способа построения на предмет его применимости к разным вариантам начальных условий, а также на предмет единственности или неединственности решения, получаемого описанным способом.

Известные задачи [ править | править код ]

• Задача Аполлония о построении окружности, касающейся трех заданных окружностей. Если ни одна из заданных окружностей не лежит внутри другой, то эта задача имеет 8 существенно различных решений.
• Задача Брахмагупты о построении вписанного четырехугольника по четырем его сторонам.

Построение правильных многоугольников [ править | править код ]

Античным геометрам были известны способы построения правильных n-угольников для n = 2 k <displaystyle n=2^> , n = 3 ⋅ 2 k <displaystyle n=3cdot 2^> , n = 5 ⋅ 2 k <displaystyle n=5cdot 2^> и n = 3 ⋅ 5 ⋅ 2 k <displaystyle n=3cdot 5cdot 2^> . cdot p_<1>cdots p_> , где p i <displaystyle p_> — различные простые числа Ферма. В 1836 году Ванцель доказал, что других правильных многоугольников, которые можно построить циркулем и линейкой, не существует.

Неразрешимые задачи [ править | править код ]

Следующие три задачи на построение были поставлены ещё древними греками:

• трисекция угла — разбить произвольный угол на три равные части;
• удвоение куба — построить ребро куба вдвое большего по объёму, чем данный куб;
• квадратура круга — построить квадрат, равный по площади данному кругу.

Лишь в XIX веке было строго доказано, что все эти три задачи неразрешимы при использовании только циркуля и линейки. Доказательство неразрешимости этих задач построения было достигнуто с помощью алгебраических методов, основанными на теории Галуа [1] . В частности, невозможность построения квадратуры круга следует из трансцендентности числа π.

Другая известная и неразрешимая с помощью циркуля и линейки задача — построение треугольника по трём заданным длинам биссектрис [2] . Эта задача остаётся неразрешимой даже при наличии инструмента, выполняющего трисекцию угла, например томагавка. [3]

Допустимые отрезки для построения с помощью циркуля и линейки [ править | править код ]

С помощью этих инструментов возможно построение отрезка, который по длине:

1. равен сумме длин нескольких отрезков;
2. равен разности длин двух отрезков;
3. численно равен произведению длин двух отрезков;
4. численно равен частному от деления длин двух отрезков;
5. численно равен квадратному корню из длины заданного отрезка (следует из возможности построения среднего геометрического двух отрезков, см. иллюстрацию). [4]

Для построения отрезка с длиной численно равной произведению, частному и квадратному корню из длин заданных отрезков необходимо задание на плоскости построения единичного отрезка (то есть отрезка длины 1), иначе задача неразрешима из-за отсутствия масштаба. Извлечение корней из отрезков с иными натуральными степенями, не являющимися степенью числа 2, невозможны с помощью циркуля и линейки.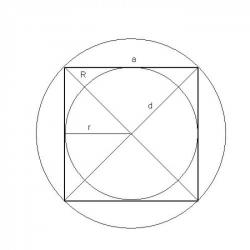 Так, например, невозможно при помощи циркуля и линейки из единичного отрезка построить отрезок длиной 2 3 <displaystyle <sqrt[<3>]<2>>> . Из этого факта, в частности, следует неразрешимость задачи об удвоении куба. [5]

Возможные и невозможные построения [ править | править код ]

С формальной точки зрения, решение любой задачи на построение сводится к графическому решению некоторого алгебраического уравнения, причем коэффициенты этого уравнения связаны с длинами заданных отрезков. Поэтому можно сказать, что задача на построение сводится к отысканию действительных корней некоторого алгебраического уравнения.

Поэтому удобно говорить о построении числа — графического решения уравнения определенного типа.

Исходя из возможных построений отрезков возможны следующие построения:

• Построение решений линейных уравнений.
• Построение решений уравнений, сводящихся к решениям квадратных уравнений.

Иначе говоря, возможно строить лишь отрезки, равные арифметическим выражениям с использованием квадратного корня из исходных чисел (заданных длин отрезков). <3>-2=0,> связанное со знаменитой задачей на удвоение куба, сводящаяся к этому кубическому уравнению. Как было сказано выше, решение этого уравнения ( 2 3 <displaystyle <sqrt[<3>]<2>>> ) невозможно построить циркулем и линейкой.

Возможность построить правильный 17-угольник следует из выражения для косинуса центрального угла его стороны:

cos ⁡ ( 2 π 17 ) = − 1 16 + 1 16 17 + 1 16 34 − 2 17 + <displaystyle cos <left(<frac <2pi ><17>>
ight)>=-<frac <1><16>>;+;<frac <1><16>><sqrt <17>>;+;<frac <1><16>><sqrt <34-2<sqrt <17>>>>;+;> + 1 8 17 + 3 17 − 34 − 2 17 − 2 34 + 2 17 , <displaystyle +<frac <1><8>><sqrt <17+3<sqrt <17>>-<sqrt <34-2<sqrt <17>>>>-2<sqrt <34+2<sqrt <17>>>>>>,> что, в свою очередь, следует из возможности сведения уравнения вида x F n − 1 = 0 , <displaystyle x^>-1=0,> где F n <displaystyle F_> — любое простое число Ферма, с помощью замены переменной к квадратному уравнению.

Popular

Основы черчения

Строительное

Машиностроительное

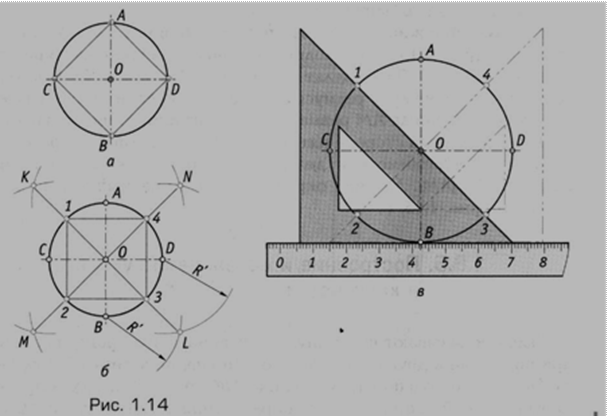
Построение вписанного в окружность правильного шестиуголь­ника. Построение шестиугольника основано на том, что сторона его равна радиусу описанной окружности. Поэтому для построения доста­точно разделить окружность на шесть равных частей и соединить най­денные точки между собой (фиг. 60, а).

Правильный шестиугольник можно построить, пользуясь рейсшиной и угольником 30X60°. Для выполнения этого построения принимаем горизонтальный диаметр окружности за биссектрису углов 1 и 4 (фиг. 60, б), строим стороны 1 —6, 4—3, 4—5 и 7—2, после чего прово­дим стороны 5—6 и 3—2.

Построение вписанного в окружность равностороннего треуголь­ника. Вершины такого треугольника можно построить с помощью циркуля и угольника с углами в 30 и 60° или только одного цир­куля.

Рассмотрим два способа построения вписанного в окружность рав­ностороннего треугольника.

Первый способ (фиг. 61,a) основан на том, что все три угла треугольника 7, 2, 3 содержат по 60°, а вертикальная прямая, прове­дённая через точку 7, является одновременно высотой и биссектрисой угла 1. Так как угол 0—1—2 равен 30°, то для нахождения стороны

1—2 достаточно построить по точке 1 и стороне 0—1 угол в 30°. Для этого устанавливаем рейсшину и угольник так, как это показано на фигуре, проводим линию 1—2, которая будет одной из сторон искомого треугольника. Чтобы построить сторону 2—3, устанавливаем рейсшину в положение, показанное штриховыми линиями, и через точку 2 прово­дим прямую, которая определит третью вершину треугольника.

Второй способ основан на том, что,если построить правильный шестиугольник, вписанный в окружность, и затем соединить его вер­шины через одну, то получится равносторонний треугольник.

Для построения треугольника (фиг. 61, б) намечаем на диаметре вершину—точку 1 и проводим диаметральную линию 1—4.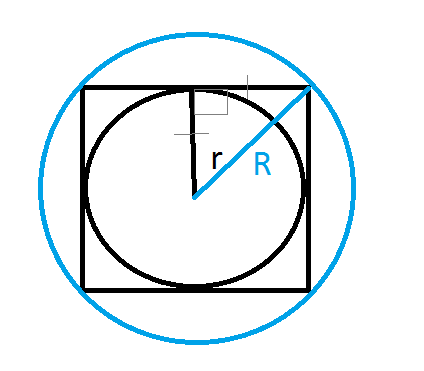 Далее из точки 4 радиусом, равным D/2, описываем дугу до пересечения с окруж­ностью в точках 3 и 2. Полученные точки будут двумя другими вер­шинами искомого треугольника.

Построение квадрата, вписанного в окружность. Это построение можно выполнить при помощи угольника и циркуля.

Первый способ основан на том, что диагонали квадрата пере­секаются в центре описанного круга и наклонены к его осям под углом 45°. Исходя из этого, устанавливаем рейсшину и угольник с углами 45° так, как это показано на фиг. 62, а, и отмечаем точки 1 и 3. Далее через эти точки проводим при помощи рейсшины горизонтальные сто­роны квадрата 4—1 и 3—2. Затем с помощью рейсшины по катету угольника проводим вертикальные стороны квадрата 1—2 и 4—3.

Второй способ основан на том, что вершины квадрата делят пополам дуги окружности, заключённые между концами диаметра (фиг. 62, б). Намечаем на концах двух взаимно перпендикулярных диа­метров точки А, В и С и из них радиусом у описываем дуги до вза­имного их пересечения.

Далее через точки пересечения дуг проводим вспомогательные пря­мые, отмеченные на фигуре сплошными линиями. Точки их пересече­ния с окружностью определят вершины 1 и 3; 4 и 2. Полученные таким образом вершины искомого квадрата соединяем последовательно между собою.

Построение вписанного в окружность правильного пятиугольника.

Чтобы вписать в окружность правильный пятиугольник (фиг. 63), про­изводим следующие построения.

Намечаем на окружности точку 1 и принимаем её за одну из вер­шин пятиугольника. Делим отрезок АО пополам. Для этого радиусом АО из точки А описываем дугу до пересечения с окружностью в точ­ках M и В. Соединив эти точки прямой, получим точку К, которую соединяем затем с точкой 1. Радиусом, равным отрезку A7, описываем из точки К дугу до пересечения с диаметральной линией АО в точке H. Соединив точку 1 с точкой H, получим сторону пятиугольника. Затем раствором циркуля, равным отрезку 1H, описав дугу из вершины 1 до пересечения с окружностью, найдём вершины 2 и 5.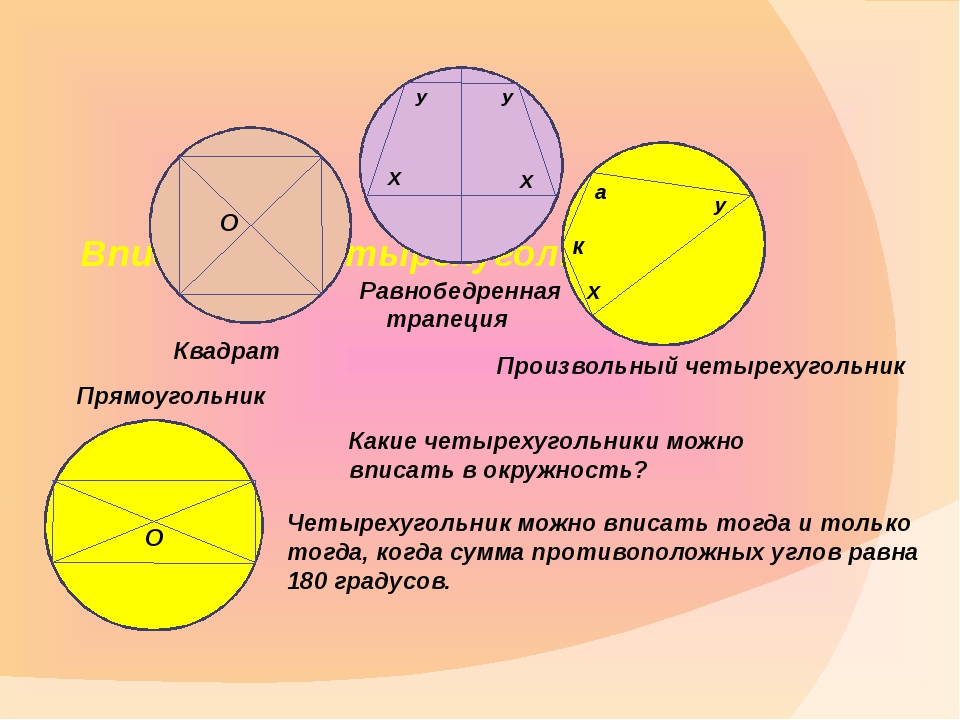 Сделав тем же раствором циркуля засечки из вершин 2 и 5, получим остальные вер­шины 3 и 4. Найденные точки последовательно соединяем между собой.

Построение правильного пятиугольника по данной его стороне.

Для построения правильного пятиугольника по данной его стороне (фиг. 64) делим отрезок AB на шесть равных частей. Из точек А и В радиусом AB описываем дуги, пересечение которых даст точку К. Через эту точку и деление 3 на прямой AB проводим вертикальную прямую.

Далее от точки К на этой прямой откладываем отрезок, равный 4/6 AB.

Получим точку 1—вершину пятиугольника. Затем радиусом, равным АВ, из точки 1 описываем дугу до пересечения с дугами, ранее проведён­ными из точек А и В. Точки пересечения дуг определяют вершины пятиугольника 2 и 5. Найденные вершины соединяем последовательно между собой.

Построение вписанного в окружность правильного семиугольника.

Пусть дана окружность диаметра D; нужно вписать в неё правильный семиугольник (фиг. 65). Делим вертикальный диаметр окружности на семь равных частей. Из точки 7 радиу­сом, равным диаметру окружности D, описываем дугу до пересечения с про­должением горизонтального диаметра в точке F. Точку F назовём полюсом многоугольника. Приняв точку VII за одну из вершин семиугольника, прово­дим из полюса F через чётные деления вертикального диаметра лучи, пересече­ние которых с окружностью определят вершины VI, V и IV семиугольника. Для получения вершин / — // — /// из точек IV, V и VI проводим до пересечения с окружностью горизонтальные прямые. Найденные вершины соединяем после­довательно между собой. Семиугольник может быть построен путём проведе­ния лучей из полюса F и через нечётные деления вертикального диаметра.

Приведённый способ годен для построения правильных многоуголь­ников с любым числом сторон.

Деление окружности на любое число равных частей можно произ­водить также, пользуясь данными табл. 2, в которой приведены коэф­фициенты, дающие возможность определять размеры сторон правильных вписанных многоугольников.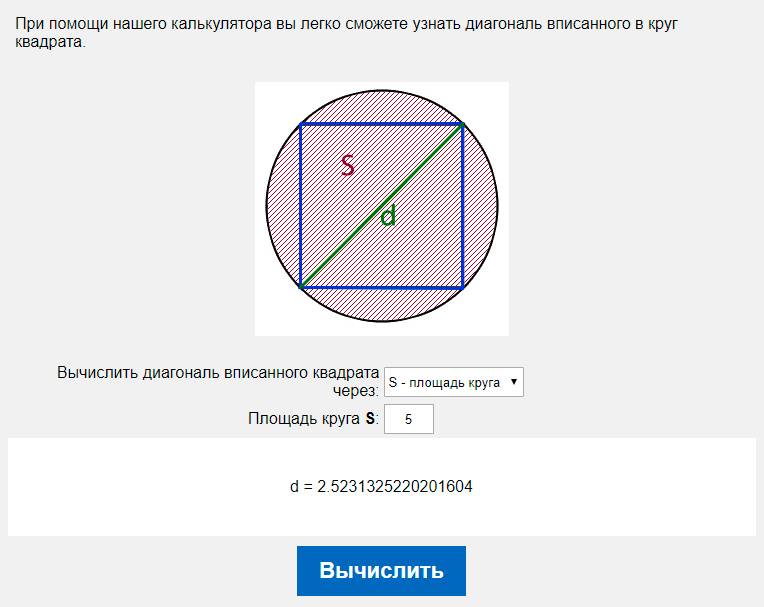

В первой колонке этой таблицы указаны числа сторон правильного вписанного многоугольника, а во второй—коэффициенты.

Длина стороны заданного многоугольника получится от умножения радиуса данной окружности на коэффициент, соответствующий числу сторон этого многоугольника.

Анализируя различные положения квадрата и окружности относительно точки зрения и линии горизонта а также правила их изображения в перспективе легко обнаружить общие закономерности. Геометричес­кая связь этих фигур определяется тем, что вокруг любой окружности можно описать квадрат, а также в лю­бой квадрат можно вписать окружность.

Как вписать окружность в квадрат?

Рассмотрите рисунок 48. Квадрат и вписанная в него окружность имеют общий центр — точку пересече­ния диагоналей квадрата. Окружность касается сторон квадрата в точках 1,2,3,4.Точки касания делят стороны квадрата пополам. Для того чтобы изобразить вписанную в квадрат окружность (в перспективном рисунке — эл­липс) необходимо определить положение осей эллипса и найти точки, задающие его размеры (точки 1 — 4).

Горизонтальный квадрат.

Найдите точки касания на перспективном рисунке горизонтально расположенного квадрата (рис.49): для этого через точку пересечения диагоналей проведите прямые, параллельные сторонам квадрата и ухо­дящие с ними в одну точку схода.

Окружность, лежащая в горизонтальной плоскости, изображается в виде эллипса с вертикальной и го­ризонтальной осями. Проведите через точку пересечения диагоналей вертикальную линию — малую ось эллип­са. Большая ось эллипса перпендикулярна малой оси и проходит через точку, смещенную от пересечения ди­агоналей квадрата (центра окружности) ближе к зрителю (рис.50). Таким образом, мы получили две оси эл­липса и четыре точки, определяющие его габариты. Продолжите рисунок: сначала легкими движениями ка­рандаша наметьте эллипс, затем уточните линию, добиваясь того, чтобы она действительно касалась сторон квадрата в точках

1,2,3,4. Проверьте симметричность полученного эллипса относительно его осей (рис. 51).

перспективный рисунок простых геометрических тел

Вертикальный квадрат.

При вертикальном положении квадрата точки 1,2,3,4найдите, как и в предыдущем примере: прове­дите через точку пересечения диагоналей квадрата прямые, параллельные его сторонам (рис.52). Несколь­ко сложнее определить направление осей эллипса. Для решения этой задачи представьте, что изображаемый нами эллипс является основанием цилиндра, лежащего на горизонтальной плоскости (рис. 53). Ось цилиндра всегда перпендикулярна большой оси эллипса основания и совпадает с его малой осью. Проведите ось ци­линдра через точку пересечения диагоналей квадрата. Ее направление можно найти, опираясь на знание и опыт рисования куба, или взять с натуры, если таковая имеется. Таким образом, мы определили положение малой оси эллипса. А большая ось будет ей перпендикулярна и пройдет через точку, смещенную от пересе­чения диагоналей — центра окружности — ближе к зрителю (рис.

54). На двух осях и по четырем точкам сна­чала наметьте эллипс легкими линиями, а затем уточните рисунок (рис.55).

Заметим, что эллипс, вписанный в квадрат, часто получается несимметричным относительно осей, а потому его приходится уточнять и, как следствие, изменять очертания квадрата. В этом случае работа идет как бы методом последовательных приближений и исправлений, что трудно и долго. Часто на рисунках остаются не вполне правильные квадраты и не вполне правильные эллипсы, а лишь фигу­ры, близкие к ним. Правильный эллипс нарисовать легче, чем построить правильный квадрат в перспекти­ве, поэтому задачу грамотного изображения квадрата современная методика рисования предлагает решать с помощью эллипса, вокруг которого описывается квадрат.

Квадрат вписанный в окружность формулы. Формула нахождения площади круга через радиус. Примеры решения задач

Круг – это видимая совокупность множества точек, которые находятся на одинаковом расстоянии от центра. 2. Другими словами диаметр во 2 степени равен стороне квадрата во 2 степени, умноженной на 2.

Вычислив значение длины диаметра круга, можно узнать и его радиус, после чего воспользоваться одной их формул определения площади круга.

Площадь сектора круга

Сектор – это часть круга, ограниченная 2 радиусами и дугой между ними. Чтобы узнать его площадь, нужно измерить угол сектора. После этого необходимо составить дробь, в числителе которой будет значение угла сектора, а в знаменателе – 360. Чтобы высчитать площадь сектора, значение, полученное в результате деления дроби, нужно умножить на площадь круга, вычисленную по одной из вышеперечисленных формул.

Чтобы формула нахождения радиуса вписанной окружности в квадрат r была правильно рассчитана, необходимо изначально вспомнить какими свойствами обладает данная фигура. У квадрата:

• все углы прямые, то есть, равны 90°;
• все стороны, как и углы, равны;
• диагонали равны, точкой пересечения бьются строго пополам и пересекаются под углом 90°.

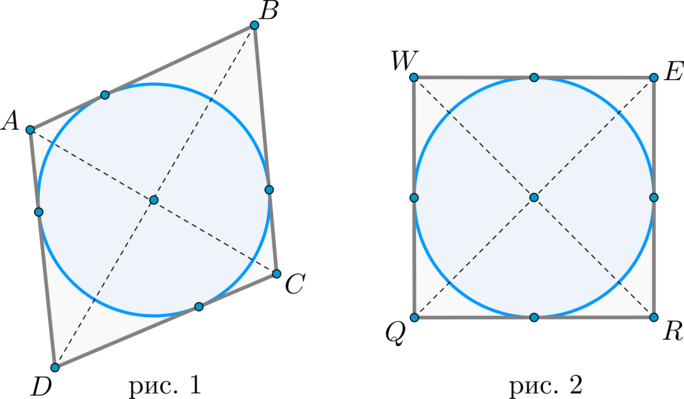
При этом вписанная в выпуклый многоугольник окружность обязательно касается всех его сторон. Обозначим квадрат ABCD , точку пресечения его диагоналей O . Как видно на рисунке 1, пересечение линий АС и ВD дают равнобедренный треугольник АОВ , в котором стороны АО =ОВ , углы ОАВ =АВО =45°, а угол АОВ =90°. Тогда радиусом вписанной окружности в квадрат будет не что иное, как высота ОЕ полученного равнобедренного треугольника АОВ .

Если предположить, что сторона квадрата равна у , то формула нахождения радиуса вписанной окружности в квадрат будет выглядеть следующим образом:

Объяснение : в равнобедренном треугольнике АОВ высота ОЕ или радиус r делят основание АВ пополам (свойства), образовывая при этом прямоугольный треугольник с прямым угол ОЕВ . В маленьком треугольнике ЕВО основание ОВ образует со сторонами ОЕ и ЕВ углы по 45°.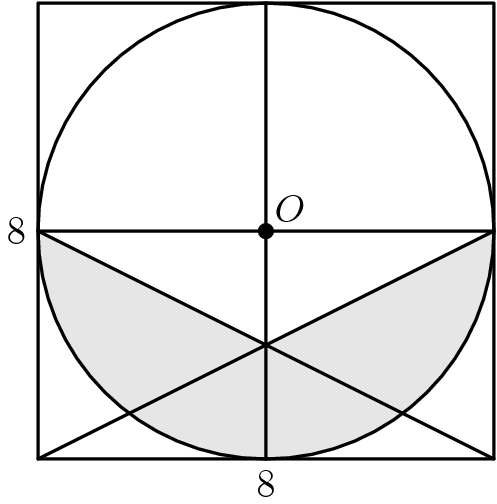 Значит треугольник ЕВО еще и равнобедренный. Стороны ОЕ и ЕВ равны.

Для наглядности приведем численный пример нахождения величины радиуса вписанной окружности в квадрат со стороной равной 13 см. В данном случае значение вписанного радиуса будет равно:

Легко решить и обратную задачу. Предположим, что известен радиус вписанной окружности – 9 см, тогда анализируя пример нахождения величины радиуса вписанной окружности в квадрат, можно найти сторону квадрата:
Находим из этого уравнения неизвестное значение: .

Вокруг квадрата также можно описать окружность. В этом случае каждая вершина фигуры будет касаться окружности. Следующая формула нахождения радиуса описанной окружности около квадрата будет находиться еще проще. В этом случае R описанной окружности будет равен половине диагонали квадрата. В буквенном виде формула выглядит так (рисунок 2):

Объяснение : после проведения диагоналей ABCD образовались два одинаковых прямоугольных треугольника АВС = CDA . Рассмотрим один из них. В треугольнике CAD :

• угол CDA=90°;
• стороны AD =CD . Признак равнобедренного треугольника;
• угол DAC равен ACD . Они равны по 45°.

Чтобы найти в этом прямоугольном треугольнике гипотенузу АС , необходимо воспользоваться теоремой Пифагора:
, отсюда
Поскольку окружность касается вершин квадрата, а точка пересечения его диагоналей является центром описанной окружности (свойства), то отрезок ОС и будет радиусом окружности. Он является половинкой гипотенузы. Это утверждение вытекает из свойств равнобедренного треугольника или свойств диагоналей квадрата. Потому формула нахождения радиуса описанной окружности около квадрата в нашем случае имеет следующий вид:

Поскольку AD =CD , а свойства квадратного корня позволяют вынести одно из подкоренных выражений, тогда формула приобретает вид:

Численный пример нахождения величины радиуса описанной окружности около квадрата будет таким.
Предположим, что диагональ квадрата равна , тогда:

Как найти площадь круга? Сначала найдите радиус. Учитесь решать простые и сложные задачи.

Круг — это замкнутая кривая. Любая точка на линии окружности будет находиться на одинаковом расстоянии от центральной точки. Круг — это плоская фигура, поэтому решать задачи с нахождением площади просто. В этой статье мы рассмотрим, как найти площадь круга, вписанного в треугольник, трапецию, квадрат, и описанного около этих фигур.

Чтобы найти площадь данной фигуры, нужно знать, что такое радиус, диаметр и число π.

Радиус R — это расстояние, ограниченное центром окружности. Длины всех R-радиусов одной окружности будут равными.

Диаметр D — это линия между двумя любыми точками окружности, которая проходит через центральную точку. Длина этого отрезка равна длине R-радиуса, умноженной на 2.

Число π — это неизменная величина, которая равна 3,1415926. В математике обычно это число округляется до 3,14.

Формула нахождения площади круга через радиус:

Примеры решения заданий по нахождению S-площади круга через R-радиус:

Задача: Найдите площадь окружности, если ее радиус равен 7 см.

Решение: S=πR², S=3,14*7², S=3,14*49=153,86 см².

Ответ: Площадь окружности равна 153,86 см².

Формула нахождения S-площади круга через D-диаметр:

Примеры решения заданий по нахождению S, если известен D:

————————————————————————————————————————-

Задача: Найдите S круга, если его D равен 10 см.

Решение: P=π*d²/4, P=3,14*10²/4=3,14*100/4=314/4=78,5 см².

Ответ: Площадь плоской круглой фигуры равна 78,5 см².

Нахождение S круга, если известна длина окружности:

Сначала находим, чему равен радиус. Длина окружности рассчитывается по формуле: L=2πR, соответственно радиус R будет равен L/2π. Теперь находим площадь круга по формуле через R.

Рассмотрим решение на примере задачи:

———————————————————————————————————————-

Задача: Найдите площадь круга, если известна длина окружности L — 12 см.

Решение: Сначала находим радиус: R=L/2π=12/2*3,14=12/6,28=1,91.

Теперь находим площадь через радиус: S=πR²=3,14*1,91²=3,14*3,65=11,46 см².

Ответ: Площадь круга равна 11,46 см².

Найти площадь круга, вписанного в квадрат просто. Сторона квадрата — это диаметр круга. Чтобы найти радиус, нужно сторону разделить на 2.

Формула нахождения площади круга, вписанного в квадрат:

Примеры решения задач по нахождению площади круга, вписанного в квадрат:

———————————————————————————————————————

Задача №1: Известна сторона квадратной фигуры, которая равна 6 сантиметров. Найдите S-площадь вписанной окружности.

Решение: S=π(a/2)²=3,14(6/2)²=3,14*9=28,26 см².

Ответ: Площадь плоской круглой фигуры равна 28,26 см².

————————————————————————————————————————

Задача №2 : Найдите S круга, вписанного в квадратную фигуру и его радиус, если одна сторона равна a=4 см.

Решайте так : Сначала найдем R=a/2=4/2=2 см.

Теперь найдем площадь окружности S=3,14*2²=3,14*4=12,56 см².

Ответ: Площадь плоской круглой фигуры равна 12,56 см².

Немного сложнее находить площадь круглой фигуры, описанной около квадрата. Но, зная формулу, можно быстро подсчитать данное значение.

Формула нахождения S круга, описанного около квадратной фигуры:

Примеры решения заданий по нахождению площади окружности, описанной около квадратной фигуры:

Задача

Окружность, которая вписана в треугольную фигуру — это круг, который касается всех трех сторон треугольника. В любую треугольную фигуру можно вписать круг, но только один. Центром круга будет точка пересечения биссектрис углов треугольника.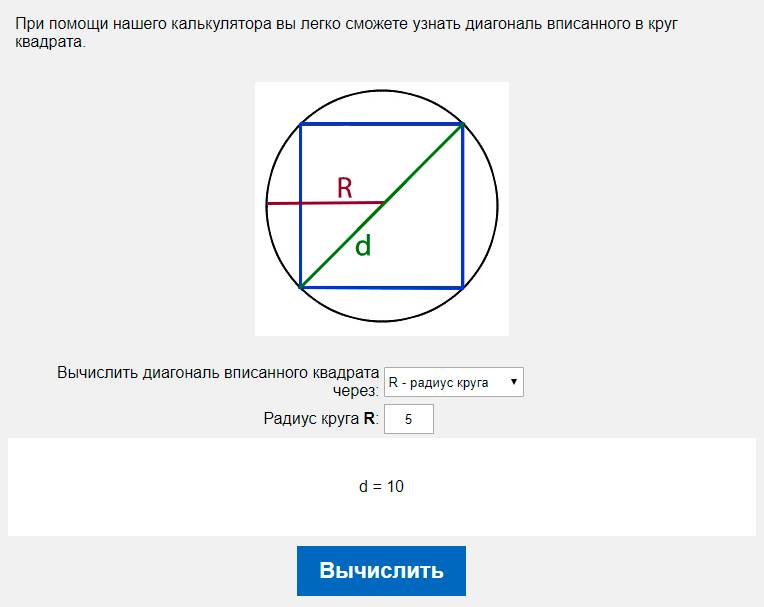

Формула нахождения площади круга, вписанного в равнобедренный треугольник:

Когда будет известен радиус, площадь можно вычислить по формуле: S=πR².

Формула нахождения площади круга, вписанного в прямоугольный треугольник:

Примеры решения заданий:

Задача №1

Если в этой задаче нужно найти еще и площадь круга с радиусом 4 см, то сделать это можно по формуле: S=πR²

Задача №2

Решение:

Теперь, когда известен радиус, можно найти площадь круга через радиус. Формулу смотрите выше по тексту.

Задача №3

Площадь круга, описанного около прямоугольного и равнобедренного треугольника: формула, примеры решения задач

Все формулы по нахождению площади круга сводятся к тому, что сначала нужно найти его радиус. Когда известен радиус, то найти площадь просто, как было описано выше.

Площадь круга, описанного около прямоугольного и равнобедренного треугольника находится по такой формуле:

Примеры решения задач:

Вот еще пример решения задачи с использованием формулы Герона.

Решать подобные задачи сложно, но их можно осилить, если знать все формулы. Такие задачи школьники решают в 9 классе.

Площадь круга, вписанного в прямоугольную и равнобедренную трапецию: формула, примеры решения задач

У равнобедренной трапеции две стороны равны. У прямоугольной трапеции один угол равен 90º. Рассмотрим, как найти площадь круга, вписанного в прямоугольную и равнобедренную трапецию на примере решения задач.

Например, в равнобедренную трапецию вписана окружность, которая в точке касания делит одну сторону на отрезки m и n.

Для решения этой задачи нужно использовать такие формулы:

Нахождение площади окружности, вписанной в прямоугольную трапецию, производится по следующей формуле:

Если известна боковая сторона, то можно найти радиус через это значение. Высота боковой стороны трапеции равна диаметру окружности, а радиус — это половина диаметра. Соответственно, радиус равен R=d/2.

Примеры решения задач:

Трапецию можно вписать в окружность, когда сумма ее противолежащих углов равна 180º. Поэтому вписать можно только равнобокую трапецию. Радиус для вычисления площадь круга, описанного около прямоугольной или равнобедренной трапеции, рассчитывается по таким формулам:

Примеры решения задач:

Решение: Большое основание в данном случае проходит через центр, так как в окружность вписана равнобедренная трапеция. Центр делит это основание ровно пополам. Если основание АВ равно 12, тогда радиус R можно найти так: R=12/2=6.

Ответ: Радиус равен 6.

В геометрии важно знать формулы. Но все их невозможно запомнить, поэтому даже на многих экзаменах разрешается пользоваться специальным формуляром. Однако важно уметь находить правильную формулу для решения той или иной задачи. Тренируйтесь в решении разных задач на нахождение радиуса и площади окружности, чтобы уметь правильно подставлять формулы и получать точные ответы.

Видео: Математика | Вычисление площадей круга и его частей

Кругом называется часть плоскости, ограниченная окружностью. Основным показателем и для окружности, и для круга является радиус. Если он задан, площадь круга можно вычислить по основной формуле S=πR2, где S – площадь круга, R – радиус окружности, ограничивающей круг, а π – константа, равная 3,14. В условиях задачи может быть дана длина окружности. Она равна L=2πR. В этом случае сначала необходимо вычислить радиус, разделив заданную величину L на 2π, то есть воспользоваться формулой R=L/2π.

По сторонам вписанного четырехугольника

В окружность, ограничивающую круг, может быть вписан четырехугольник, сумма противолежащих углов которого составляет 180°, то есть это квадрат или прямоугольник. В этом случае диаметр описанной вокруг четырехугольника окружности является одновременно диагональю. Если в условиях заданы размеры сторон четырехугольника, найти эту диагональ не составит особого труда, воспользовавшись теоремой Пифагора. Диагональ делит квадрат или прямоугольник на два прямоугольных треугольника, то есть является гипотенузой каждого из этих треугольников. Соответственно, найти ее можно, сложив квадраты сторон четырехугольника, то есть по формуле d2=a2+b2. Чтобы найти площадь круга, даже не нужно из полученного результата извлекать квадратный корень, поскольку R=d/2. Чтобы найти квадрат радиуса, достаточно квадрат диаметра разделить на 4.

По параметрам вписанного в окружность треугольника

Способ решения этого варианта задачи зависит от того, какой треугольник вписан и какие его параметры заданы. Если треугольник прямоугольны, алгоритм решения будет таким же, как для квадрата или , поскольку сторона, противолежащая прямому углу, всегда является диаметром описанной окружности. Если даны размеры катетов, возведите каждый из них в квадрат и найдите сумму, а затем полученный результат разделите на 4 и умножьте на число π. Если треугольник равносторонний, придется выполнить несколько дополнительных построений, чтобы в итоге получились прямоугольные треугольники, параметры которых вам известны. Например, в окружность с центром О вписан равносторонний треугольник АВС, сторона которого вам задана. Проведите высоты AN, ВM и СQ. Рассмотрите, например, прямоугольный треугольник AQO. Вам известна его гипотенуза AQ, которая равна половине стороны исходного треугольника, а также все углы, так что найти длину отрезка AQ, который одновременно является радиусом круга, площадь которого вам надо найти, можно по теореме синусов или косинусов.

Читайте статью, чтобы знать, как находить площадь квадрата разными способами.

Квадрат — это равносторонний прямоугольник. У данного правильного и плоского четырехугольника равенство во всех сторонах, углах и диагоналях. Из-за того что существует такое равенство, формула для вычисления площади и других характеристик, немного видоизменяется по сравнению с иными математическими фигурами. Но это не делает задачи слишком сложными. Давайте разберем все формулы и решения задач в этой статье.

Площадь S прямого и квадратного угольников вычисляется по формуле: a умножить на b . Но так как у квадрата полное равенство сторон, то его площадь будет равна: S=(a) во второй степени . Как узнать величину стороны квадрата, зная его площадь?

• Если известна площадь квадратного угольника, то сторону находим путем исчисления площади из-под квадратного корня.
• К примеру, площадь угольника равна 49, то чему равняется сторона?
• 49=(а) во второй степени . Решение: а=корень из 49=7. Ответ: 7 .

Если нужно найти сторону квадратного угольника, площадь которого состоит слишком длинного числа, тогда воспользуйтесь калькулятором. Наберите сначала число площади, а потом нажмите знак корня на клавиатуре калькулятора. Получившееся число и будет ответом.

В этом примере будем использовать теорему Пифагора. У квадрата все стороны равны, а диагональ d мы будем рассматривать как гипотенузу прямоугольного равнобедренного треугольника с катетом а . Теперь находим диагональ квадрата, если известна его площадь:

• Чтобы не расписывать всю теорему Пифагора будем решать по второму варианту: d=a√2, где а — это сторона квадрата.
• Итак, нам известна площадь квадрата, например, она равна 64. Значит одна сторона а=√64=8.
• Получается d=8√2 . Корень из 2 не получается целым числом, поэтому в ответе можно написать именно так: d=8√2 . Но, если хочется вычислить значение, тогда воспользуйтесь калькулятором: √2= 1,41421356237 и умножьте на 8, получается 11, 3137084 .

Важно: Обычно в математике не оставляют в ответе цифры с большим количеством чисел после запятой. Нужно округлять или оставить с корнем. Поэтому ответ на нахождение диагонали, если площадь равна 64 будет таким: d=8√2 .

Формула нахождения площади квадрата через диагональ простая:

Теперь напишем решение по нахождению площади квадрата через диагональ:

• Диагональ d=8.
• 8 в квадрате равняется 64.
• 64 разделить на 2 равно 32.
• Площадь квадрата равна 32.

Совет: У этой задачи есть еще одно решение через теорему Пифагора, но оно более сложное. Поэтому используйте решение, которое мы рассмотрели.

Периметр квадратного угольника P — это сумма всех сторон. Чтобы найти его площадь, зная его периметр, нужно сначала вычислить сторону квадратного угольника. Решение:

• Допустим периметр равен 24. Делим 24 на 4 стороны, получается 6 — это одна сторона.
• Теперь используем формулу нахождения площади, зная чему равна сторона квадратного угольника: S=а в квадрате, S=6 в квадрате=36 .
• Ответ: 36

Как видите, зная периметр квадрата, просто найти его площадь.

Радиус R — это половина диагонали квадрата, вписанного в окружность. Теперь можем найти диагональ по формуле: d=2*R . Далее находим площадь квадрата вписанного в окружность с заданным радиусом:

• Диагональ равна 2 умножить на радиус. Например радиус равен 5, тогда диагональ равна 2*5=10 .
• Выше было описано, как находить площадь квадрата, если известна диагональ: S=диагональ в квадрате разделить на 2. S=10*10 и разделить на 2=50.
• Ответ — 50 .

Эта задача немного сложнее, но тоже легко решаемая, если знать все формулы.

На картинке видно, что радиус вписанной окружности равен половине стороны. Сторона находится по формуле обратной той, которая изображена на картинке: а=2*r . Потом уже находим площадь квадрата описанного около окружности с заданным радиусом по формуле S=а в квадрате . Решение:

• Допустим, радиус равен 7. Сторона квадрата а равна 2*7=14.
• S=14 в квадрате=196 .

Если понять суть решения подобных задач, то можно решать их быстро и просто. Давайте рассмотрим еще несколько примеров.

Примеры решения задач на тему «Площадь квадрата»

Чтобы закрепить пройденный материал и запомнить все формулы, необходимо решить несколько примеров задач на тему «Площадь квадрата». Начинаем с простой задачи и движемся к решению более сложных: Примеры решения сложных задач на тему «Площадь квадрата»

Теперь вы знаете, как пользоваться формулой площади квадрата, а значит, вам любая задача под силу. Успехов в дальнейшем обучении!

Видео: Вычисление площади квадрата

Как рисовать окружность на курсах рисунка каранадашом

Правильно нарисовать окружность в ракурсе куда легче на курсах рисунка карандашом, если сначала нарисовать квадрат в нужном нам перспективном искажении, а в него уже вписать окружность.

Когда мы в студии Артакадемия на уроках рисунка карандашом вписываем окружность в квадрат, они соприкасаются в четырех точках по всем сторонам квадрата (см. Рис. 154) – и это сохраняется в любом ракурсе. На эти точки мы можем опираться, чтобы правильно построить окружность – которая в перспективном сокращении превратится в эллипс (Рис. 155.) (см. Заметку X).

Рисунок 154

 

Рисунок 155

Расположениеэтих четырех (и любых других) опорных точек и в положении анфас, и в перспективе определяется диагоналями, про которые уже шел разговор в Главах IIIи IV. Когда мы видим фигуры анфас, еще четыре опорные точки будут находиться там, где диагонали пересекаются с вписанной окружностью (Рис. 156). С помощью линий Iи II(Рис. 157 и Рис. 99, Глава IV), эти точки можно переложить на фигуры в перспективном искажении.

Рисунок 156

Рисунок 157

На практике, нам не нужно рисовать квадрат или круг анфас – мы сразу начинаем с изображения в нужном перспективном искажении, а потом с помощью диагоналей и пересекающихся линий устанавливаем точки A, B, C, D (посередине боковых сторон квадрата) (Рис. 158). Еще четыре опорные точки мы находим следующим образом: отмерьте четверть ближайшей к вам стороны квадрата и используя это как длину стороны, нарисуйте квадрат и проведите через него диагональ.

Измерьте длину этой диагонали и отметьте эту длину в обе стороны от центра ближайшей к вам стороны (А-1, А-2). От точек 1 и 2 проведите линии к точке схода, чтобы найти точки, где окружность будет пересекаться с диагоналями квадрата. Нарисуйте окружность в ракурсе с опорой на эти восемь точек.

Рисунок 158

Если у вас под рукой не будет этой информации и вы забудете, как правильно проводить измерения, вы можете найти точки 1 и 2 приблизительно (хотя это и не будет до конца точно), расположив их от углов на расстоянии чуть менее одной шестой длины стороны (Рис. 159).

Рисунок 159

Заметка X. Самый длинный диаметр эллипса, сформированного таким образом, будет находиться ниже центральной линии квадрата. Если вы разрежете окружность (Рис. 160) и сложите вместе по линии центра эллипса, две половины совпадут.

Рисунок 160

Окружность, вид снизу

Окружность в ракурсе, располагающаяся выше уровня наших глаз, может быть нарисована с использованием тех же опорныхточекквадрата в ракурсе. Ближайшая сторона квадрата будет, конечно же, также его верхней стороной, поскольку мы смотрим на нижнюю его плоскость (Рис. 161).

В вертикальных положениях (Рис. 162) никаких новых сложностей с построением окружности возникнуть не должно, так что дополнительные объяснения не нужны. На самом деле, Рис. 158 может использоваться для иллюстрации построений в четырех положениях: 1) вид сверху, 2) вид снизу – если перевернуть изображение так, чтобы оно оказалось вверх ногами, 3) вертикальное положение, вид слева – если повернуть страницу с изображением по часовой стрелке, 4) вертикальное положение, вид справа – если повернуть страницу в противоположном направлении.

Вписанная в квадрат окружность, видимая под углом

Построить вписанную окружность, если она находится под углом, ненамного более сложно. Это может достаточно часто пригодиться на практике, если вы, например, рисуете колонну, стоящую на прямоугольном основании.

Практика (Рис. 163). Нарисуйте квадрат под углом, или самостоятельно выбрав две точки схода, или же ориентируясь на Рис. 94. Проведите горизонтальную линию основания от ближайшего угла, и на них отметьте те же деления, как показано на Рис. 158. Поделите ближайшую сторону квадрата (1-2) согласно пропорциям, которые были объяснены в Главе III, Рис. 64-65.

Больше об академическом рисуноке можно прочесть в наших материалах:

Что такое академический рисунок как классическое искусство?

Летний набор на курсы академического рисунка

Курсы академического рисунка — как правильно строить объекты в перспективе.

Обучение академическому рисунку — теория света, полутона и тени

Предварительная подготовка к курсам рисования карандашом

Упражнения по академическому рисунку

Правила линейной перспективы и их применение на курсах рисунка карандашом

Описание академического рисунка губ человека с примерами набросков — программа для среднего и высшего уровня подготовки.

Академический рисунок губ человека карандашом

Диаметр круга, описанного вокург квадрата и шестигранника. Таблица: Диаметр заготовок — круглых прутков под квадраты и шестигранники в мм в зависимости от размеров квадратов и шестигранников.

	Адрес этой страницы (вложенность) в справочнике dpva.ru:  главная страница  / / Техническая информация / / Математический справочник / / Геометрические фигуры. Свойства, формулы: периметры, площади, объемы, длины. Треугольники, Прямоугольники и т.д. Градусы в радианы. / / Плоские фигуры. Свойства, стороны, углы, признаки, периметры, равенства, подобия, хорды, секторы, площади и т.д.  / / Диаметр круга, описанного вокург квадрата и шестигранника. Таблица: Диаметр заготовок — круглых прутков под квадраты и шестигранники в мм в зависимости от размеров квадратов и шестигранников. Поделиться:    Таблица: Диаметр заготовок — круглых прутков под квадраты и шестигранники в мм в зависимости от размеров квадратов и шестигранников. Диаметр круга, описанного вокург квадрата и шестигранника. S D1 под квадрат D2 под шестигранник S D1 под квадрат D2 под шестигранник S D1 под квадрат D2 под шестигранник 1 1.41 1.16 18 25.46 20.79 35 49.50 40.42 2 2.83 2.31 19 26.87 21.95 36 50.91 41.58 3 4.24 3.47 20 28.28 23.10 37 52.32 42.74 4 5.66 4.62 21 29.70 24.26 38 53.74 43.89 5 7.07 5.78 22 31.11 25.41 39 55.15 45.05 6 8.48 6.93 23 32.53 26.57 40 56.57 46.20 7 9.90 8.09 24 33.94 27.72 41 57.97 47.36 8 11.31 9.24 25 35.36 28.88 42 59.40 48.51 9 12.73 10.40 26 36.77 30.09 43 60.80 49.57 S D1 под квадрат D2 под шестигранник S D1 под квадрат D2 под шестигранник S D1 под квадрат D2 под шестигранник 10 14.14 11.55 27 38.18 31.19 44 62.22 50.82 11 15.56 12.71 28 39.60 32.34 45 63.64 51.96 12 16.97 13.86 29 41.01 33.50 46 65.05 53.13 13 18.38 15.02 30 42.43 34.65 47 66.49 54.09 14 19.80 16.17 31 43.84 35.81 48 67.88 55.44 15 21.21 17.32 32 45.25 36.96 49 69.29 56.60 16 22.63 18.48 33 46.66 38.12 50 70.71 57.80 17 24.04 19.64 34 48.08 39.27 — — — Поиск в инженерном справочнике DPVA. Введите свой запрос: Поиск в инженерном справочнике DPVA. Введите свой запрос: Адрес этой страницы (вложенность) в справочнике dpva.ru:  главная страница  / / Техническая информация / / Математический справочник / / Геометрические фигуры. Свойства, формулы: периметры, площади, объемы, длины. Треугольники, Прямоугольники и т.д. Градусы в радианы. / / Плоские фигуры. Свойства, стороны, углы, признаки, периметры, равенства, подобия, хорды, секторы, площади и т.д.
Если Вы не обнаружили себя в списке поставщиков, заметили ошибку, или у Вас есть дополнительные численные данные для коллег по теме, сообщите , пожалуйста. Вложите в письмо ссылку на страницу с ошибкой, пожалуйста.
Коды баннеров проекта DPVA.ru Начинка: KJR Publisiers Консультации и техническая поддержка сайта: Zavarka Team	Проект является некоммерческим. Информация, представленная на сайте, не является официальной и предоставлена только в целях ознакомления. Владельцы сайта www.dpva.ru не несут никакой ответственности за риски, связанные с использованием информации, полученной с этого интернет-ресурса. Free xml sitemap generator

Рисунок квадрата в перспективе | СПЛАЙН

ЦЕЛЬ ЗАДАНИЯ. Понять принцип взаимодействия квадрата и окружности на перспективном рисунке. Научиться проверять правильность квадрата, вписывая в него окружность.

ПОСТАНОВКА ЗАДАНИЯ. Изобразите в перспективе горизонтальный и вертикальный квадраты. Проверьте правильность их изображения при помощи вписанных окружностей.

РЕКОМЕНДАЦИИ ПО ВЫПОЛНЕНИЮ ЗАДАНИЯ. Прежде, чем приступать к выполнению этого задания, внимательно рассмотрите схему на рис. 2.8. Точки касания сторон квадрата к окружности (точки 1, 2, 3, 4) делят стороны квадрата пополам. Средние линии квадрата и его диагонали пересекаются в центре окружности. Противолежащие стороны квадрата и соответствующие им средние линии параллельны и расположены на равном расстоянии друг от друга. Рассмотрите также рис. 2.9. На примере окружности и квадрата во фронтальной перспективе хорошо видно, что центр эллипса и центр окружности – две разные точки. Диаметр окружности, являющийся малой осью эллипса, делится точкой центра окружности на два разных по величине отрезка: ближний к зрителю – больше, дальний – меньше (по закону перспективного сокращения), а точка центра эллипса делит этот же диаметр – малую ось эллипса – ровно пополам.

Нарисовать квадрат в перспективе можно в разной последовательности, например, сначала изобразить одну прямую – сторону квадрата, а затем другую, ей перпендикулярную, отложить на этих прямых от точки их пересечения отрезки, равные стороне квадрата, а затем от полученных вершин достроить остальные стороны, сводя параллельные прямые в точки схода. Или иначе – сначала провести две параллельные прямые, а затем еще две, перпендикулярные двум первым. В любом случае эта задача кажется простой только на первый взгляд. На самом деле слишком много позиций (степень схождения параллельных сторон квадрата, их направления и размеры) рисовальщику приходится определять на основании своего личного опыта, а его, как известно, иногда бывает недостаточно. Именно поэтому правильность квадрата необходимо проверить, например, вписав в него окружность. При любом положении квадрата для того, чтобы вписать в него окружность (в перспективном рисунке – эллипс), необходимо найти точки касания сторон квадрата к вписанной окружности (точки 1 – 4) и определить положение осей эллипса. Если вписанный эллипс касается сторон квадрата в заданных точках и симметричен относительно осей, то квадрат нарисован верно.

Горизонтальный квадрат. Нарисуйте горизонтальный квадрат по представлению (рис. 2.10). Найдите точки касания, для этого через точку пересечения диагоналей проведите прямые, параллельные сторонам квадрата и уходящие с ними в одну точку схода (рис. 2.11). Окружность, лежащая в горизонтальной плоскости, изображается на перспективном рисунке в виде эллипса с вертикальной и горизонтальной осями. Проведите через точку пересечения диагоналей вертикальную линию – малую ось эллипса. Большая ось эллипса перпендикулярна малой оси и проходит через точку, смещенную от пересечения диагоналей квадрата (центра окружности) ближе к зрителю (рис. 2.12). Таким образом, мы получили две оси эллипса и четыре точки, определяющие его габариты. Продолжите рисунок: сначала легкими движениями карандаша наметьте эллипс, затем уточните линию, добиваясь того, чтобы она действительно касалась сторон квадрата в точках 1, 2, 3, 4 (рис. 2.13). Проверьте симметричность полученного эллипса относительно его осей.

Вертикальный квадрат. При вертикальном положении квадрата точки 1, 2, 3, 4 найдите, как и в предыдущем примере: проведите через точку пересечения диагоналей квадрата прямые, параллельные его сторонам (рис. 2.14).

Несколько сложнее определить направление осей эллипса. Чтобы это сделать, представьте, что изображаемый эллипс является основанием цилиндра, лежащего на горизонтальной плоскости (рис. 2.15). Ось цилиндра на перспективном рисунке всегда перпендикулярна большой оси эллипса основания и совпадает с его малой осью. Проведите ось цилиндра через точку пересечения диагоналей квадрата. Направление этой оси можно определить, опираясь на опыт рисунка с натуры. Задача значительно упрощается в том случае, если вертикальный квадрат, в который вы вписываете окружность, является гранью куба. Тогда ось цилиндра (она же малая ось эллипса) параллельна горизонтальным ребрам куба и на рисунке идет с ними в одну точку схода. Таким образом, мы определили положение малой оси эллипса. Большая ось будет ей перпендикулярна и пройдет через центр эллипса, смещенный от пересечения диагоналей (центра окружности) ближе к зрителю (рис. 2.16). На двух осях и по четырем точкам касания изобразите эллипс (рис. 2.17).

На рисунках, иллюстрирующих последовательность вписывания окружности в горизонтальный и вертикальный квадраты, представлены идеальные ситуации. В действительности эллипс, вписанный в квадрат, часто получается несимметричным относительно осей, а потому его приходится уточнять и, как следствие, изменять очертания квадрата. В этом случае работа идет как бы методом последовательных приближений и уточнений, что трудно и долго. Часто на рисунках остаются не вполне правильные квадраты и не вполне правильные эллипсы, а лишь фигуры, близкие к ним.

Правильный эллипс нарисовать легче, чем построить правильный квадрат в перспективе. Именно поэтому современная методика предлагает не проверять и исправлять подобным образом уже нарисованные квадраты, а строить их, описывая вокруг окружности.

Сколько квадратов можно упаковать в круг?

Приношу свои извинения за столь длинный ответ. Мой подход состоит в том, чтобы начать с теоретического максимума и гарантированного минимума. Когда вы подходите к проблеме, вы можете использовать эти значения, чтобы определить, насколько хорош любой используемый вами алгоритм. Если вы можете придумать лучший минимум, то можете использовать его вместо этого.

Мы можем определить верхний предел для задачи, просто используя площадь окружности

Upper Limit = floor( (PI * (r pow 2)) / (L * L) )

Где L-ширина или высота упаковываемых квадратов, а r-радиус окружности, в которую вы упаковываете квадраты. Мы уверены, что это верхний предел, потому что а) мы должны иметь дискретное число ящиков и б) мы не можем занимать больше места, чем площадь круга. (Формальное доказательство будет работать где-то в духе предположения, что у нас есть еще один ящик, чем этот, тогда сумма площадей ящиков будет больше площади круга).

Таким образом, с верхним пределом в руке мы можем теперь взять любое решение, которое существует для всех кругов, и назвать его минимальным решением.

Итак, давайте рассмотрим решение, которое существует для всех кругов, взглянув на самый большой квадрат, который мы можем поместить внутри круга.

Самый большой квадрат, который вы можете поместить внутри круга, имеет 4 точки по периметру и имеет ширину и длину sqrt(2) * radius (используя теорему Пифагора и используя радиус для длины более коротких ребер)

Итак, первое, что мы замечаем, это то, что если sqrt(2) * radius меньше размера ваших квадратов, то вы не можете поместить ни одного квадрата в круг, потому что, в конце концов, это самый большой квадрат, который вы можете поместить.

Теперь мы можем сделать простое вычисление, чтобы разделить этот большой квадрат на правильную сетку квадратов, используя L, который вы указали, что даст нам по крайней мере одно решение проблемы. Таким образом, у вас есть сетка квадратов внутри этого максимального квадрата. Количество квадратов, которые вы можете поместить в одну строку этой сетки, равно

floor((sqrt(2) * radius)/ L)

И поэтому это минимальное решение утверждает, что вы можете иметь по крайней мере

Lower Limit = floor((sqrt(2) * radius)/ L) pow 2

количество квадратов внутри круга.

Так что на случай, если вы заблудились, все, что я сделал, это взял самый большой квадрат, который мог поместиться внутри круга, а затем упаковал как можно больше квадратов в правильную сетку внутри него, чтобы дать мне хотя бы одно решение.

Если вы получаете ответ на 0 для этого этапа, то вы не можете поместить какие-либо квадраты внутри круга.

Теперь, вооружившись теоретическим максимумом и абсолютным минимумом, вы можете начать пробовать любой эвристический алгоритм, который вам нравится для упаковки квадратов. Простой алгоритм состоял бы в том, чтобы просто разбить круг на строки и поместить в каждую строку столько квадратов, сколько сможете. Затем вы можете взять этот минимум в качестве ориентира, чтобы убедиться, что вы придумали лучшее решение. Если вы хотите потратить больше вычислительной мощности на поиск лучшего решения, вы используете теоретическое в качестве ориентира для того, насколько вы близки к теоретическому лучшему.

И если вас это волнует, вы могли бы выяснить, какой максимальный и минимальный теоретический процент покрытия дает вам минимальный алгоритм, который я идентифицировал. Самый большой квадрат всегда покрывает фиксированное отношение (pi/4 или около 78.5% внутренней площади круга, я думаю). Таким образом, максимальный теоретический минимум составляет 78.5% обложек. И минимум нетривиальный (т. е. теоретический минимум — это когда вы можете поместить только 1 квадрат внутри самого большого квадрата, что происходит, когда квадраты, которые вы упаковываете, на 1 больше половины ширины и высоты самого большого квадрата, который вы можете поместить в круг. В основном вы занимаете чуть более 25% внутреннего квадрата с 1 упакованным квадратом, что означает, что вы получаете приблизительное покрытие около 20%

кругов, вписанных в квадраты

Когда круг вписан в квадратный , то диаметр круга равна длине стороны квадрата.

Вы можете найти периметр и площадь квадрата, если дан по крайней мере один размер круга или квадрата.

Для квадрата с длиной стороны s используются следующие формулы.

Периметр = 4 s

Площадь = s 2

Диагональ = s 2

Точно так же вы можете найти длина окружности а также площадь круга , когда дан хотя бы один размер круга или квадрата.

Для круга с радиусом р используются следующие формулы.

Окружность = 2 π р

Площадь = π р 2

Пример 1:

Найдите периметр квадрата.

Когда круг вписан в квадрат, диаметр круга равен длине стороны квадрата.

Итак, длина стороны квадрата равна 6 см.

Периметр п квадрата со стороной s дан кем-то п знак равно 4 s .

Заменять 6 для s в п знак равно 4 s .

п знак равно 4 ( 6 ) знак равно 24

Периметр квадрата равен 24 см.

Пример 2:

Какова площадь круга, вписанного в квадрат площади? 64 квадратные единицы?

Когда круг вписан в квадрат, длина каждой стороны квадрата равна диаметру круга. То есть диаметр вписанной окружности равен 8 единиц и, следовательно, радиус 4 единицы измерения.

Площадь круга радиуса р единиц А знак равно π р 2 .

Заменять р знак равно 4 в формуле.

А знак равно π ( 4 ) 2 знак равно 16 π ≈ 50.24

Следовательно, площадь вписанного круга составляет около 50,24 квадратные единицы.

Круг, вписанный в квадрат

Мы видели, что когда квадрат вписан в круг, мы можем выразить все свойства квадрата или круга (площадь, периметр, окружность, радиус, длина стороны), если мы знаем просто длина радиуса или длина стороны квадрата.

Теперь мы увидим, что то же самое верно, когда круг вписан в квадрат.

Задача 1

В квадрат вписан круг радиуса «r». Найдите формулы для длины стороны, длины диагонали, периметра и площади квадрата через r.

Стратегия

При решении аналогичной задачи о квадрате, вписанном в круг, ключевым моментом было то, что диагональ квадрата — это диаметр круга.

Здесь аналогичный ключевой вывод состоит в том, что радиус круга равен половине длины стороны квадрата.

Так как круг вписан в квадрат, сторона квадрата касается круга.По определению, радиус перпендикулярен касательной в точке касания.

Радиус образует угол 90 ° с одной стороной квадрата. Таким образом, он параллелен соседней стороне квадрата. Это верно и для других радиусов. Это означает, что четырехугольник, образованный двумя радиусами и двумя смежными сторонами квадрата, также является квадратом.

В этом новом квадрате сторона равна радиусу. Мы можем сделать это для каждой из остальных 4 сторон большего внешнего квадрата.В каждом из них радиусы образуют квадраты меньшего размера. У меньших квадратов все стороны равны радиусу.

Стороны двух таких соседних маленьких квадратов образуют сторону большего внешнего квадрата. Поскольку каждая из сторон меньшего квадрата равна r, сторона внешнего квадрата равна 2r.

Формальное доказательство:

(1) OA ⊥ AB // Учитывая, что AB касается окружности O, касательная линия перпендикулярна радиусу
(2) m∠OAB = 90 ° // Определение перпендикулярной линии
( 3) m∠ABC = 90 ° // Все внутренние углы квадрата прямые.
(4) OA || CB // Теорема об обратных последовательных внутренних углах
(5) OC ⊥ CB // Учитывая, что CB касается окружности O, касательная перпендикулярна радиусу
(6) m∠OCB = 90 ° // Определение перпендикулярной линии
(7) m∠ABC = 90 ° // Все внутренние углы квадрата прямые
(8 ) OC || AB // Теорема об обратных последовательных внутренних углах
(9) OC = OA // Все радиусы окружности равны
(10) OCBA — параллелограмм // (4), (8), определение параллелограмма
(11) BA = OC = r // противоположные стороны параллелограмма равны

И аналогично

(12) OEDA — параллелограмм
(13) AD = OE = r // противоположные стороны параллелограмма равны
(14) | BD | = | BA | + | AD | = r + r = 2r

Хорошо, теперь, когда мы это сделали, остальное очень просто.Площадь квадрата равна квадрату длины стороны, поэтому она равна 4r ² . Периметр в 4 раза больше длины стороны, поэтому он равен 4r. А длину диагонали можно вычислить по теореме Пифагора, и она равна 2r√2.

Теперь давайте сделаем обратное, найдя свойства вписанного круга по длине стороны квадрата.

Задача 2

В квадрат вписан круг со стороной, равной «а». Найдите формулы для радиуса, диаметра, длины окружности и площади круга через букву «а».

Как мы показали выше, радиус круга равен половине длины стороны квадрата, поэтому r = a / 2. Диаметр в два раза больше радиуса, поэтому d = a. Длина окружности равна d · π, поэтому C = πa. Наконец, площадь равна π · r ² , поэтому A = π · a ² /4.

Этот тип проблем с вписанной формой часто имеет компонент, связанный с нахождением области между формами, которая является неправильной, поэтому давайте рассмотрим пример.

Задача 3

В квадрат вписан круг со стороной 10 единиц.Найдите область заштрихованной области:

Стратегия

Ключ к решению этого типа задач — найти области правильных форм. Затем выразите заштрихованную область как разницу между ними. В этом случае мы легко можем найти площадь круга и квадрата.

Разница между ними в четырех углах, образованных двумя краями квадрата и дугой, составляющей четверть круга. Из-за симметрии все эти формы имеют одинаковую площадь. Таким образом, заштрихованная область составляет половину разницы между площадями круга и квадрата.

Решение

A _{квадрат} = a · a = 10 · 10 = 100
A _круг = π · a ² /4 = π · 10 ² /4 = 25π
A _{заштрихованный} = (Квадрат -A _круг ) / 2 = (100-25π) /2=12,5 (4-π)

Радиус круга в квадрате

Привет, Лори. Надеюсь, эта диаграмма подходит под ваше описание:

Вы хотите найти r , радиус окружности.

Уравнение круга:

(x — h) ² + (y — k) ² = r ²

, где (h, k) — центр окружности.Итак, если мы можем определить уравнение круга, мы можем определить его радиус.

Начнем с того, что поместим начало координат в нижний левый угол. Тогда центр — это (r, r) , поэтому у нас есть

(x — r) ² + (y — r) ² = r ²

Где находится угол желтого прямоугольника там, где он касается круга? Это (2, 1) .

Итак, мы можем подставить это значение (x, y) в уравнение круга:

(2 — r) ² + (1 — r) ² = r ²

Лори, можешь закончить задачу отсюда?

Надеюсь, это поможет,
Стивен Ла Рок.

Привет Лори,

Когда я прочитал ваш вопрос, я не понял его, но Сью поняла. Когда я прочитал решение Сью, я увидел другой подход к нему, поэтому взял ее диаграмму, добавил две линии и пометил три точки.

Длина CA составляет r . Какова длина AB ? Какая длина г. до н.э. ? Что вам говорит теорема Пифагора? Пенни

Лори ответила.

Это вопрос для иска и пенни. Сначала Сью, я поставил единицы вместо
буквы r и получил ответ 1, но это не кажется правильным. Неужели
я вообще это делаю правильно?

Следующий пенни, я знаю, что теорема Пифагора говорит мне a ² + b ² = c ² но
Я не совсем уверен, что делать после этого.

Спасибо за все

Привет, Лори. Да, одно из решений уравнения — 1, но это не соответствует диаграмме.Тем не менее, это соответствует большей части математического описания
. Взгляните на эту диаграмму ниже.

Вы видите, что это подходит под описание?
— В квадрат вписан круг? да
— Маленький прямоугольник с высотой 2 фута и стороной 1 фут слева в квадрате, касающемся угла круга? да, прямоугольник находится в верхнем левом углу квадрата, а его угол касается круга.

Вот почему значение 1 работает. Однако для диаграммы, которую я нарисовал ранее, должно быть другое решение, и оно есть.R = 5 работает?

Стивен Ла Рок>

Лори.

На моей диаграмме треугольник CAB является прямоугольным, и поэтому вы можете применить теорему Пифагора.

Если длина стороны AB составляет a , длина стороны BC составляет b , а длина стороны CA (гипотенуза) составляет c , тогда
a ² + b ² = c ² .Если вы используете диаграмму, чтобы найти длины AB и BC , то теорема Пифагора дает вам уравнение, которое эквивалентно уравнению, найденному Сью, (2 — r) ² + (1 — r ) ² = r ² .

Пенни

Calculus — Максимальное количество упаковок круга в прямоугольник

Рассмотрим следующую схему треугольной упаковки:

Если окружности имеют радиус $ r $, то каждая пара горизонтальных красных линий находится на расстоянии $ r $ друг от друга, и они находятся на расстоянии $ r $ от краев.Каждая пара вертикальных синих линий находится на расстоянии $ r \ sqrt 3 $ друг от друга, и они все еще находятся на расстоянии $ r $ от краев.

Итак, если вы хотите, чтобы треугольная упаковка имела $ m $ кругов в каждом столбце и $ n $ столбцов, тогда прямоугольник должен быть не менее $ (2m + 1) \ cdot r $ единиц в высоту и $ (2 + (n -1) \ sqrt3) \ cdot r $ единиц в длину. (Кроме того, если высота прямоугольника составляет всего $ 2m \ cdot r $ единиц, мы можем чередовать столбцы с кругами $ m $ и $ m-1 $.)

Если прямоугольник равен $ 257 \ times 157 $, а радиус круга равен $ \ sqrt {\ frac {10} {\ pi}} $, то:

• Если мы сделаем 257 $ вертикальным размером, тогда прямоугольник будет немного больше $ 144 \ cdot r $ единиц в высоту и немного больше $ (2 + 49 \ sqrt3) \ cdot r $ единиц в ширину.Таким образом, мы можем расположить круги в столбцы по $ 50 $, которые чередуются между $ 72 $ и $ 71 $ кругами, для кругов $ 25 \ cdot 72 + 25 \ cdot 71 = 3575 $.
• Если мы сделаем $ 157 $ вертикальным размером, тогда прямоугольник будет немного больше $ 87 \ cdot r $ единиц в высоту и немного больше $ (2 + 82 \ sqrt3) \ cdot r $ единиц в ширину. Таким образом, мы можем расположить круги в $ 83 $ столбцах, по $ 43 $ в каждом, для $ 3569 $ кругов.

Мы выбираем первый вариант, который дал нам большее значение.

Если вы хотите знать точное количество кругов, которые могут уместиться, нет ничего лучше, чем этот расчет.Но вы можете оценить количество кругов, которые уместятся, зная, что предельная плотность треугольной упаковки равна $ \ frac {\ pi} {2 \ sqrt 3} $.

Прямоугольник $ 257 \ times 157 $ имеет площадь $ 40349 $, но можно использовать не более $ \ frac {\ pi} {2 \ sqrt 3} $ этой площади: не более $ \ frac {40349 \ pi} {2 \ sqrt 3} \ около 36592,5 $. Если все круги имеют площадь 10 $, то в этой области может поместиться не более 3659 $ кругов. Как видите, это завышенная оценка, потому что мы не используем пространство по краям упаковки максимально эффективно.2} {\ text {Площадь кристалла}} — \ frac {\ pi \ times (\ text {Диаметр пластины})} {\ sqrt {2 \ times \ text {Площадь кристалла}}} $$ Поскольку $ \ text {Диаметр пластины} / 2 = \ text {Радиус пластины} $, $ \ pi \ times \ text {Диаметр пластины} = \ text {Окружность пластины} $ и $ \ sqrt {\ text {Площадь кристалла} } = \ text {Длина кромки квадратного кристалла} $, приведенное выше эквивалентно $$ \ text {Количество штампов на пластину} = \ frac {\ text {Площадь пластины}} {\ text {Площадь кристалла}} — \ sqrt {\ frac {1} {2}} \ frac {\ text {Окружность пластины} } {\ text {Длина кромки квадратной матрицы}} $$ Левая часть — это количество штампов, которое вы могли бы получить, если бы пластина имела форму, которая могла быть точно заполнена штампами.В правой части указано приблизительное количество штампов, «потерянных» из-за формы диска. 2 — \ sqrt {\ frac {1} {2}} 2 \ pi \ lambda = \ pi \ lambda \ left (\ lambda — \ sqrt {2} \ right ) $$ что меньше верхней границы, полученной в другом ответе.Другими словами, оценка $ \ text {Dies per wafer} $ довольно консервативна.

кругов, вписанных в квадраты — подготовка к тесту Каплана

В этой серии мы рассмотрим многие типы геометрических сценариев, встречающихся в тесте SAT Math. Базовые знания простых формул (площадь, периметр и т. Д.) Очень важны, но есть множество ярлыков для вопросов о геометрии, которые сэкономят ваше время. Сегодня мы исследуем круги, вписанные в квадраты.
Что нужно помнить

• Центр квадрата совпадает с центром круга
• Рисуй линии! В зависимости от того, чего требует стимул, нарисуйте линии, образующие простые формы.(Квадраты можно, например, превратить в треугольники.)
• Общие углы обычно не указываются явно, за исключением случаев необходимости.
• Доверяйте картинкам, но не слишком. Выводы следует делать из фактов. То, что он выглядит как 90 градусов, еще не значит, что это так! (Многие из этих общих выводов будут подробно описаны в этой серии статей.)
• Длина не может быть отрицательной. Будьте осторожны с вопросами DS, которые ставят уравнения в контексте квадратных уравнений с двумя решениями. Если одно решение отрицательное, а другое положительное, остается только положительное решение и информации достаточно.

Для кругов:

• d = 2r, и все прямые от центра к внешней стороне равны r.
• C = 2πr = πd
• A = πr²
• НИКОГДА не используйте 2πr², если вы не добавляете области одинаковых кругов!
• Касательные линии образуют прямые углы с радиусом, который пересекает эту касательную.
• Если вы знаете r, вы знаете о круге все!
• С осторожностью используйте π = 22/7. Помните 22/7> π.

Для квадратов:

• Диагональ равна s√2, поскольку образует углы в 45 градусов.
• Пересечение диагоналей создает прямой угол.
• Когда круг вписан внутрь квадрата, сторона равна диаметру.

Обычно вам будет предоставлен один бит информации, который говорит вам многое, если не все. Если задана длина стороны квадрата на изображении выше, мы действительно можем найти длину гипотенузы внутреннего треугольника (s = d = 2r, поэтому гипотенуза = (s√2) / 2).

Затененные участки

Найдите большую область и вычтите из нее маленькую.Имея дело с кругами вместе с другими фигурами, исключите варианты ответов, в которых ТОЛЬКО есть числа π или их совсем нет. Обычно ваш ответ будет иметь вид x + yπ.

На рисунке выше изображен круг, идеально вписанный в квадрат. Заштрихованная область> 4?
(1) Площадь большого прямоугольника равна 64.
(2) Периметр заштрихованной области равен 8 + 2π.

Заявление 1: Зная площадь большого квадрата, мы также знаем длины его сторон.(Обратите внимание, что 64 — это точный квадрат, который должен быть подсказкой.) Если сторона равна 8, значит, диаметр равен 4, что означает, что радиус равен 4. На изображении мы можем видеть, что «большая фигура» — это правый верхний квадрат, ограниченный двумя радиусами и внешней границей. Как мы узнаем, что это квадрат? Две части информации: все стороны равны 4, а радиус пересекает большой квадрат под прямым углом, потому что это касательная. В этом случае площадь меньшего квадрата равна 16. Поскольку внутренний угол составляет 90 градусов (360/4), площадь сектора круга может быть представлена ​​как A = πr² / 4.Так что A = 16π / 4 = 4π.
A (закрашенный) = A (маленький квадрат) — A (сектор) = 16 — 4π <4, потому что 4π> 12. Достаточно.
Утверждение 2: Первое, что должно выскочить, — это комбинация π-члена и не-π-члена. Мы можем разумно предположить, что 8 представляет две прямые стороны периметра, а 2π — длину дуги четверти окружности, которая известна из-за внутреннего прямого угла. Если 2π = C / 4, то C = 8π. Если C = 8π, то r = 4. Отсюда мы возвращаемся к тем же рассуждениям, что и выше:
A (заштриховано) = A (маленький квадрат) — A (сектор) = 16 — 4π <4, потому что 4π> 12.Достаточный.
Каждого утверждения достаточно, , поэтому ответ — выбор D .

Два важных вывода:

1. Никогда не предполагайте без доказательств.
2. Следуйте по следу.

Сногсшибательная математическая иллюзия превращает круг в меньший квадрат

Скриншот: YouTube

Может ли большой круглый диск пройти через маленькое квадратное отверстие? Когда вы впервые это представляете, это кажется невозможным. Но благодаря математику Стэнфордского университета Тадаши Токиэда вы увидите, что — это , возможно и проще, чем вы думаете.В поучительном видео от Numberphile он демонстрирует эту иллюзию, используя пробковую подставку и лист бумаги с квадратным отверстием, вырезанным посередине. Если сложить бумагу определенным образом, отверстие внезапно станет достаточно большим, чтобы подставка могла легко пройти через отверстие.

«Я не растягивал, не говоря уже о том, чтобы порвать, — делится Токиэда, — но, тем не менее, когда я разумно складываю лист обратно, подставка проходит через квадрат, который больше отверстия. Как это возможно?»

Токиэда затем подробно объясняет, как он может подогнать подстаканники.«Это связано с внутренним размером этого листа бумаги, который является двухмерным, и с тем фактом, что этот лист развивается или процветает в окружающем трехмерном пространстве», — говорит он. «Есть немного места для локтей, есть какое-то окружающее пространство».

Если это все еще заставляет вас чесать голову, обязательно посмотрите, как Токиэда складывает бумагу. Он делает это особым образом, трансформируя лист из двух измерений в трехмерные. При этом он соединяет две стороны квадрата вместе и формирует отверстие большего размера, через которое подставка может пройти без проблем.

Прокрутите вниз, чтобы увидеть Токиеду в действии. Тогда попробуйте сами!

Кажется, большой круглый диск не может поместиться в квадратное отверстие меньшего размера, верно? Посмотрите, как математик Тадаси Токиэда доказывает, что математическая иллюзия возможна: