Изометрия сетка: Как работать с изометрией. Изометрия — это ракурс, в котором видны… | by MAD RABBIT

Как создать изометрическую и перспективную сетки в фотошопе | EnottiaART

Если вы хотите рисовать окружение , то вам не обойтись без этих двух сеток. В этой статье расскажу как их построить.

Изометрическая сетка

Изометрия- это перспектива, в которой не учитывается точка схода.

Изометрические сетки бывают симметричными и не симметричными. У изометрической сетки нет точек схода, все линии параллельны.

пример использования изометрической сетки

пример использования изометрической сетки

источник: https://www.artstation.com/artwork/xJ6k4R

источник: https://www.artstation.com/artwork/xJ6k4R

Берем инструмент кисть нужной толщины.

Проводим на листе горизонтальную линию. Для этого просто нужно провести её, одновременно зажав клавишу Shift

первая линия

первая линия

Выделяем холст и далее копировать-вставить-сдвинуть немного вверху. Т.е. Сtrl C+Ctrl V сдвинуть Ctrl V сдвинуть Ctrl V сдвинуть. Таким образом у вас появится множество слоёв, на которых есть одна ваша линия. А на холсте множество беспорядочно расположенных линий.

разместили полосы

разместили полосы

Далее выделяем все слои с линиями. С включенным инструментом «перемещение» и выбираем сверху пункт» Распределение центров по вертикали». Таким образом все линии станут равноудалены друг от друга.

равноудаленные полосы

равноудаленные полосы

Выделяем все слои, клик правой клавишей мыши и выбираем пункт «объединить слои».

сливаем слои

сливаем слои

Выделяем получившийся слой, копируем, вставляем, выделяем при помощи сочетания клавиш Ctrl T, а затем переворачиваем с зажатым shift. Таким образом получаем клетку.

клетка

клетка

Объединяем слои, Ctrl T и поворот с зажатым shift на 90 градусов.

поворот на 90

поворот на 90

Затем возьмем и сплющим по вертикале на столько, насколько это нам требуется. Чем больше сетка развернута вверх, тем меньше объекты загораживают друг друга, но тем меньшее количество поля мы видим на экране единовременно.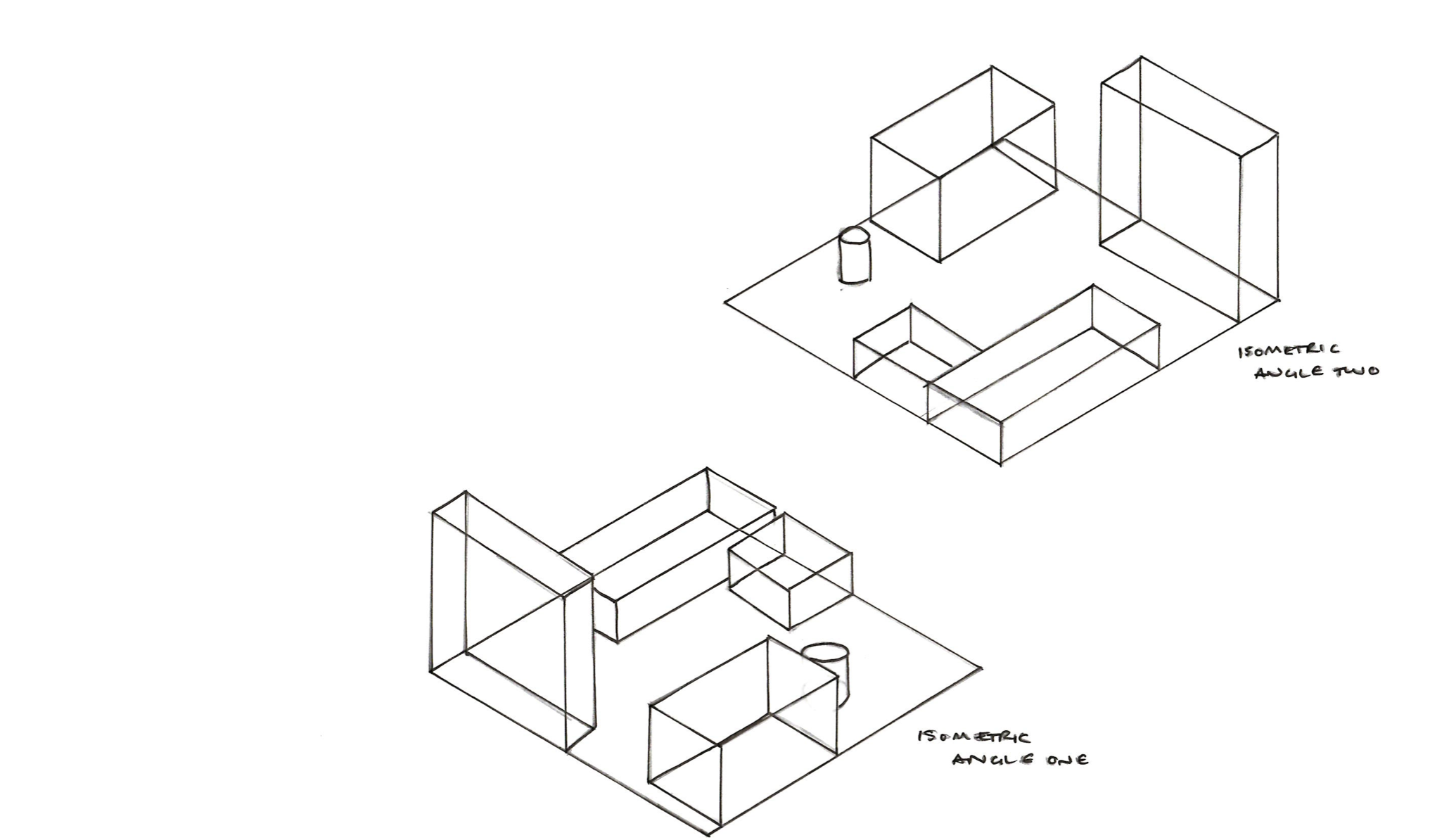 Если мы сетку сильно сплющиваем мы в экране единовременно можем видеть практически все поле, но объекты на нем начнут немножко загораживать друг друга. А если быть точным, то чем сильнее сплющим, тем больше они станут друг друга загораживать.

плющим

плющим

готовая сетка

готовая сетка

Данная сетка будет считаться симметричной. Есть еще ситуация с нераным углом, когда параллельные линии в одну сторону сплющиваются под одним углом, а те что идут в противоположную под другим. Но это случается очень редко и честно говоря, сама я не встречала такой ситуации. Потому информация чисто для справки.

ситуация с неравным углом

ситуация с неравным углом

Перспективная сетка

В отличии от изометрической в перспективной сетке множество линий сходятся в точке схода и не являются параллельными.

Выбираем инструмент многоугольник.

Далее заходим в параметр шестеренка, ставим галочку на против пункта «звезда» и плотность 99%. Справа выставляем количество строк-100.

После всех этих махинаций вы сможете создавать фигуру, которая выглядит так:

А потом делаете нечто вот такое

и даже такое

К этому делу еще нужно приноровиться, так что способ одновременно и читерский и сложный, но с ним вы сможете построить перспективную сетку в 1-2-3 точки схода. Юху!

Пример использования:

если присмотреться, то можно разглядеть ту самую сетку

если присмотреться, то можно разглядеть ту самую сетку

источник: https://www.artstation.com/artwork/58Qd2O

источник: https://www.artstation.com/artwork/58Qd2O

Изометрия в Inkscape. Как работать с изометрией

В Adobe illustrator есть 3 популярных способа работать с изометрией:

1. Используя изометрическую сетку
2. Методом SSR
3. С помощью функции 3D

На практике, чтобы нарисовать иллюстрацию, нужно уметь пользоваться всеми тремя способами. В этом уроке я расскажу о каждом из них, опишу преимущества и недостатки.

А. Изометрическая сетка

Изометрическая сетка служит исключительно вспомогательным инструментом.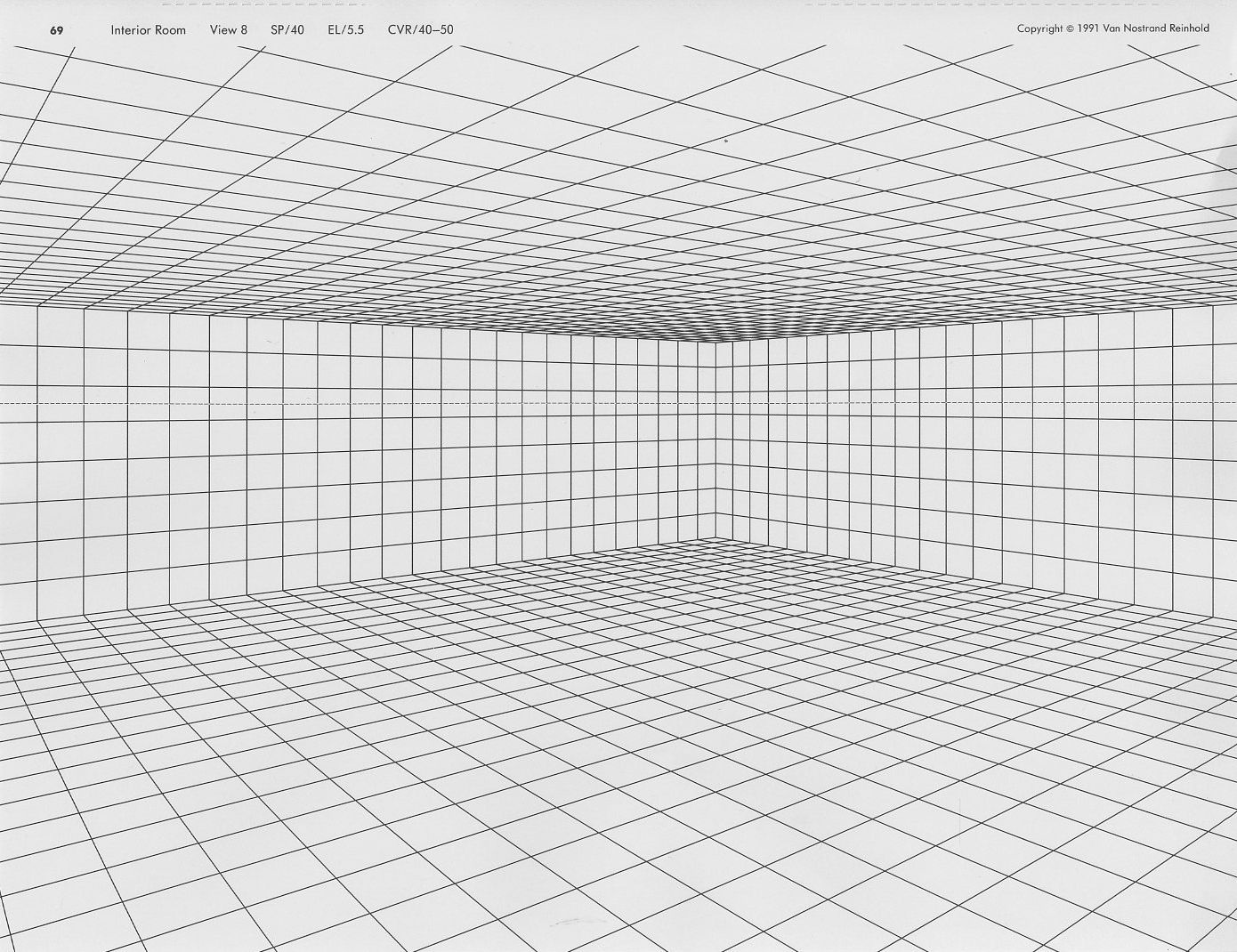

Как создать:

I. С помощью инструмента Line Segment Tool строим линию под углом 30° c длиной не менее 2000 px

II. Теперь нам нужно создать для нее много копий. Открываем эффект Effect - Distort&Transformt- Transform , во вкладке Move параметры Horizontal и Vertical отвечают за расстояние между линиями, параметр Copies за количество копий (вот это поворот!)

III. Разбираем оформление Object - Expand Appereance

IV. Дублируем группу с нашими линиями и делаем их зеркальную копию Object - Transform - Reflect

V. Превращаем получившиеся линии в направляющие View - Guides - Make Guides

Примечание: в отличии от Фотошопа, функционал Иллюстратора позволяет создавать направляющие расположенные под углом

Сетка готова. Теперь с помощью инструмента Перо, можно рисовать по нашим направляющим фигуры.

Минусы: можно рисовать только простейшие фигуры прямоугольных форм.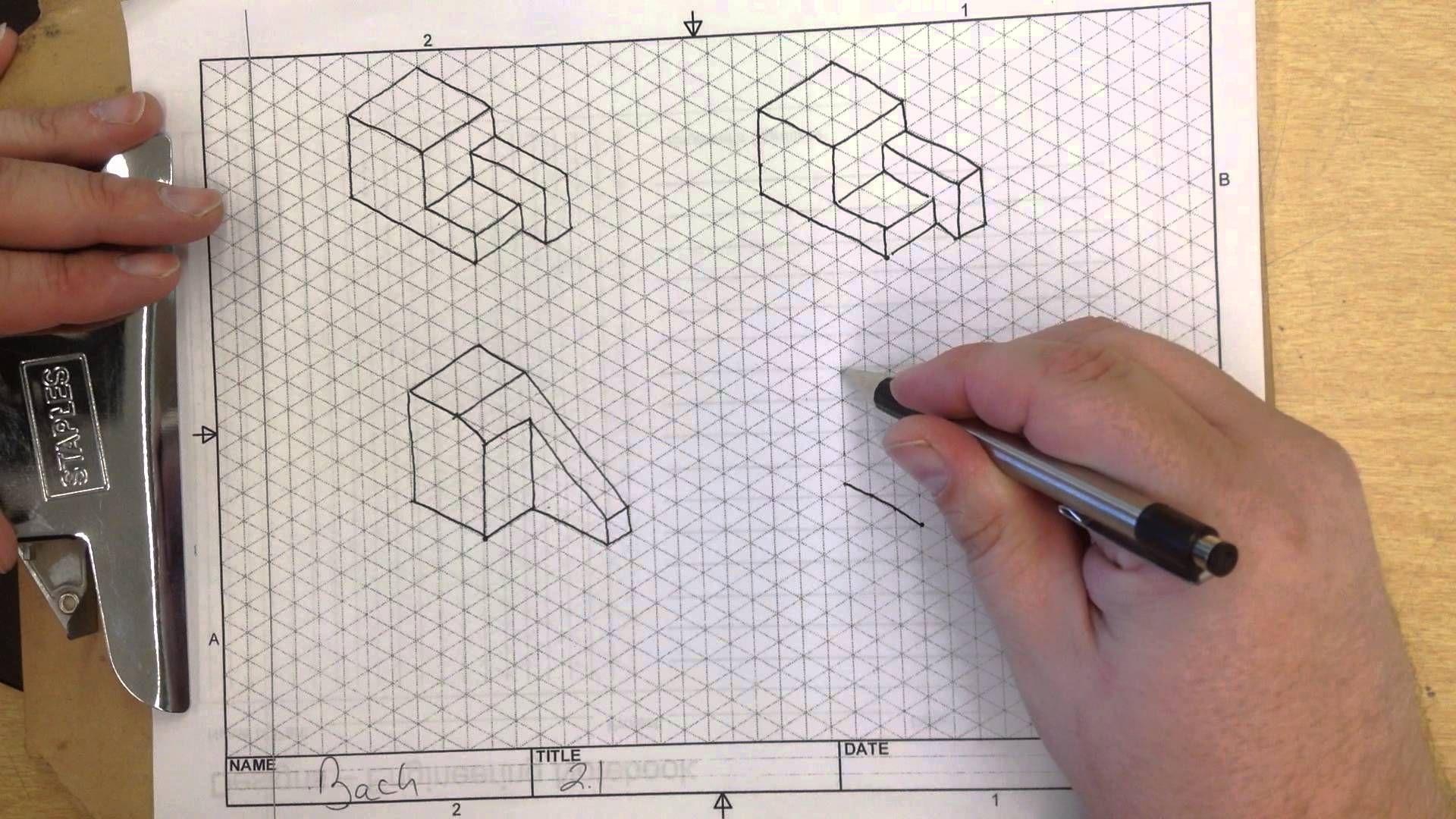 Не получится нарисовать фигуры эллипсоидной формы и фигуры сложной формы.

Однако изометрическая сетка нам пригодится при работе со следующим методом SSR, чтобы выравнивать по ней стороны фигуры.

Б. Scale Skew Rotate (SSR)

Преимущество SSR заключается в том, что можно рисовать объект в анфас, а потом переводить в изометрию.

Для этого нам нужны 3 инструмента: Масштаб (Scale Tool ), Наклон (Shear Tool ), Поворот (Rotate Tool ).

Значение параметра Scale по вертикали всегда остается неизменным 86,062% , а значения параметров Shear и Rotate выбираются в зависимости от того, какую грань изображаемого предмета мы переводим в изометрию (верхняя, левая или правая).

С помощью метода SSR можно одновременно перевести в изометрию большую группу маленьких объектов, например, клавиши на клавиатуре ноутбука.

Или сам ноутбук, предварительно сделав его развертку, а потом переведя в изометрию каждую его часть по отдельности (экран и клавиатура):

Сделать в изометрии фигуру эллипсоидной формы:

Или фигуру сложной формы, которую невозможно сходу рисовать по сетке:

Изометрическая сетка пригодится нам для того, чтобы рисовать дополнительные детали на объекте (напоминаю, в изометрии все линии должны быть строго под углом кратным 30):

В примере выше сетка помогла мне нарисовать и правильно расположить маленькие детали конвейера (деления сверху и эллипсы сбоку).

Минусы: методом SSR неудобно рисовать объекты, у которого скошенные (или скругленные) края и объекты сложной формы, которые выгоднее делать через функцию 3D.

В. 3D

В этом случае нам поможет функция 3D, которая, к счастью, имеется в функционале Иллюстратора.

Порядок действий:

I. Рисуем переднюю часть объекта в анфас

II. Применяем эффект Effect - 3D - Extrude&Bevel

III. В параметре Position выбираем значение Isometric Right или Left (Top и Bottom нам не нужны, т.к. в таком ракурсе можно спокойно нарисовать фигуру с помощью SSR).

IV. Разбираем оформление, удаляем все лишние и на выходе получаем готовую к использованию фигуру.

Кроме того, это самый быстрый способ нарисовать примитив в изометрии: всего пара кликов и фигура готова. Если бы мы делали это методом SSR - пришлось бы немного повозиться.

По сути 3D является полноценной замены метод SSR и проигрывает второму лишь в частных случаях (например, при попытке перевести в изометрию клавиатуру от ноутбука).

Выводы:

1. Универсального способа рисовать изометрию - НЕТ.
2. Эти способы не единственные, но они подходят под большинство практических задач

В этом уроке мы разобрали инструменты для работы с изометрией, т.е. освоили техническую сторону вопроса.

В следующем уроке я расскажу о композиции в изометрии, рассмотрюсамые распространенные косяки и покажу процесс построения сложного объекта.

В графическом дизайне полно подводных камней. Даже не так - это самая насыщенная подводными камнями сфера. В отличии от точных наук, здесь «точных» законов до безобразия мало, а скрытых нюансов, от которых зависит итоговый результат - до безобразия много.

На своих курсах я учу ребят делать крутую графику на которую есть спрос. Я помогаю разобрать все по полочкам и добиться на выходе результата, за который мне не будет стыдно.

Только помни: нельзя попробовать стать графическом дизайнером. Надо либо окунаться в это с головой, либо заниматься чем-то попроще. Если ты все для себя решил и хочешь максимально быстрого прогресса - 

В этом Коротком Уроке, мы покажем вам, как можно создать удобную для работы изометрическую сетку, всего за несколько простых шагов. Вы узнаете как использовать Инструмент Прямоугольная Сетка с техникой SSR, и меньше чем через две минуты, вы будете готовы к тому, чтобы создать вашу изометрическую работу.

Шаг 1

Откройте новый документ. Размеры зависят от того, что вы собираетесь рисовать с помощью нашей сетки, и тоже с цветовой моделью. Теперь мы начнем, и выберем инструмент Прямоугольная Сетка (Rectangular Grid Tool).

Шаг 2

Установите параметры для Прямоугольной Сетки. Нажмите Enter и установите Количество для Горизонтальных и Вертикальных разделителей по 30. Это величина зависит от пропорций вашей работы, так что выберите значения на ваше усмотрение.

Шаг 3

Теперь у вас есть два варианта. Вы можете указать величины для Ширины и Высоты на предыдущем шаге (что я делать не рекомендую).

В это случае вы должны установить равные значения для Ширины и Высоты, что бы получить квадратную сетку. Или вы можете проигнорировать эти значения, и нарисовать мышкой, удерживая нажатым Shift, один большой квадрат, гораздо больший, чем ваша рабочая зона (позже вы увидите почему).

То, что мы собираемся делать дальше называется SSR — метод (Scale-Shift-Rotate — Масштабируй-Сдвигай-Поворачивай). Это метод который позволяет создавать 3D изометрическую графику из 2D. Для нашей сетки мы будем использовать случай верхней плоскости из этой техники.

Шаг 4 — Масштабируй

Выберите сетку и зайдите в Объект > Трансформировать > Масштабирование (Object > Transform > Scale), выберите опцию Непропорционально и установите по Вертикали — 88,602%.

Исправление : На рисунке стоит число 86,062, но правильное значение 86.602

Шаг 5 — Сдвигайте

Сетка должна быть по прежнему выделена. Зайдите в Объект > Трансформировать > Наклон (Object > Transform > Shear) и установите значение 30 градусов.

Шаг 6 — Поворачивайте

И наконец мы должны повернуть нашу сетку. Объект > Трансформировать > Поворот (Object > Transform > Rotate) и установите Угол — 30 градусов.

Шаг 7

Теперь мы сделали нужные линии, и теперь все что нам нужно это сделать из них Направляющие (Guides). Убедитесь, что сетка выделена и зайдите в меню Просмотр > Направляющие > Создать Направляющие (Control + 5) (View > Guides > Make Guides).

Подводим Итоги

Теперь у вас есть площадка для создания идей, и это заняло только две или три минуты. Потратив немного времени на использование этой техники вы можете создать отличные изометрические иллюстрации и при этом вы знаете, что используете правильную перспективу. Развлекайтесь!

Так же, как и сетка в Adobe Illustrator, направляющие нужны для помощи при создании и редактировании объектов, но в отличие от сетки, направляющие могут располагаться под любым углом и иметь абсолютно разную форму.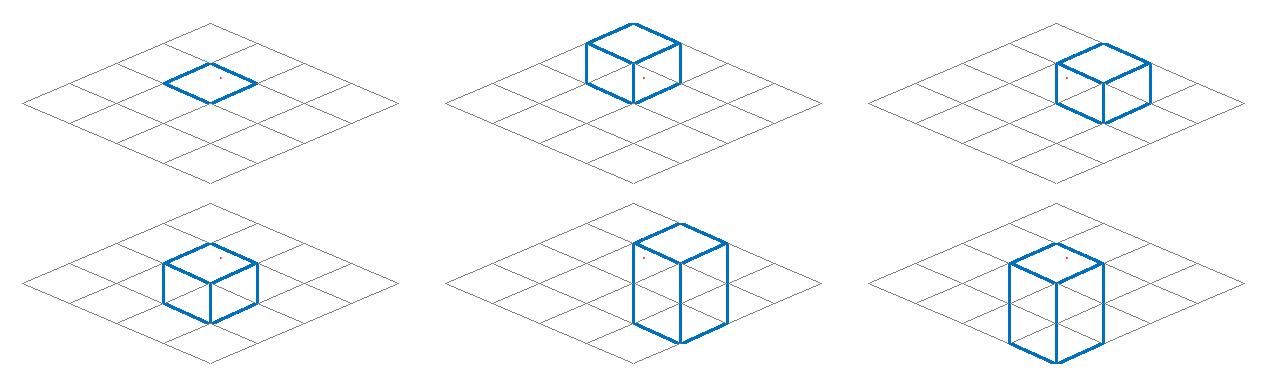

Направляющие не выводятся при печати на бумаге и видны только во время работы в программе.

Вы можете создать линейные направляющие, которые располагаются строго вертикально или горизонтально, или направляющие объекты, которые создаются из обычных векторных объектов.

• Для того чтобы создать линейную направляющую, поместите курсор над вертикальной или горизонтальной линейкой, зажмите и перетащите в нужное место. Если вы хотите ограничить линейные направляющие внутри монтажной области, а не распространять их на всю рабочую область, то вам нужно сначала выбрать инструмент Artboard и затем создать направляющие.
• Если вы хотите создать направляющую из векторного объекта, то нужно выделить этот объект и выбрать в меню View > Guides > Make Guides . Чтобы трансформировать направляющую обратно в обычный векторный объект, выберите в меню View > Guides > Release Guides .

Чтобы скрыть или показать направляющие, выберите в меню View > Hide Guides или View > Show Guides .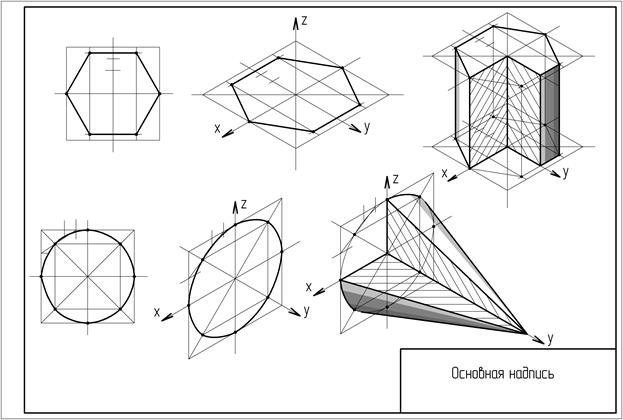

Также вы можете выбрать стиль направляющих – тип линий (сплошные или пунктирные) и цвет. Для этого перейдите в меню Edit > Preferences > Guides & Grid и измените соответствующую настройку.

По умолчанию направляющие разблокированы и вы можете свободно манипулировать ими, но при желании можете их заблокировать, чтобы случайно ничего с ними не сделать в процессе работы. Для этого выберите View > Guides > Lock Guides .

Шаг 1

Создайте новый документ в Фотошопе (Ctrl + N). Откройте PSD файл с изометрией и оттуда перенесите в созданный документ изометрическую сетку.

Шаг 2

Используя сетку, нарисуйте прямоугольник любого цвета.

Шаг 3

Создайте копию прямоугольника (Ctrl + J) и поднимите её немного, измените цвет, чтобы различать два слоя.

Шаг 4

Слой сетки можно выключить, он больше не нужен.

2. Почва

Шаг 1

Инструментом Pen Tool (P) нарисуйте боковую сторону.

Примените к ней стиль Gradient Overlay:

Шаг 2

Уменьшите заливку до 0%.

Шаг 3

Повторите процесс для правой стороны.

Шаг 4

Обрисуйте всю фигуру и примените стиль градиента. После этого уменьшите заливку до 0%.

Шаг 5

Из архива с файлами урока вставьте в наш документ изображение почвы.

Шаг 6

Выделите левую боковую сторону (удерживая CTrl, кликните на миниатюре слоя). К слою почвы добавьте маску.

Шаг 7

Наложите ту же текстуру на правую сторону.

3. Холм

Шаг 1

Вставьте фотографию ландшафта в наш документ и уменьшите непрозрачность, чтобы было видно платформу.

Шаг 2

К слою с ландшафтом добавьте маску и чёрным цветом скройте всё лишнее.

Шаг 3

Вернёмся к почве. Нужно сделать её темнее. Выберите мягкую кисть с малой непрозрачностью и чёрным цветом нарисуйте тень в углу.

Шаг 4

Продолжаем затемнять почву.

Шаг 5

Вставьте другую фотографию с землёй и наложите её на боковые стороны. Установите режим наложения Overlay. Добавьте маску и уделите время созданию деталей на боковых сторонах.

Шаг 6

Вставьте другую фотографию ландшафта. Расположите её под предыдущим слоем ландшафта. Добавьте маску и скройте лишнюю часть.

Шаг 7

Создайте новый слой и нарисуйте тень на новом ландшафте.

4. Море

Шаг 1

Вставьте фотографию моря и расположите её под всеми элементами.

Шаг 2

Выделите форму всей платформы и добавьте маску к слою с морем.

Шаг 3

Мягкой кистью поработайте над краями и скройте оставшиеся лишние детали.

Шаг 4

Нужно добавить больше волн. Для этого создайте копию фотографии моря и сдвиньте её немного. Затем поработайте с маской.

Шаг 5

Выделите слой океана (удерживая Ctrl, кликните на миниатюре слоя). После этого создайте корректирующий слой Photo Filter: Cooling Filter (80).

5. Детали

Шаг 1

Добавим больше контрастности. Выделите первый слой ландшафта.

Создайте новый слой и перейдите в меню Edit ? Stroke.

Шаг 2

К чёрной обводке примените фильтр Gaussian Blur (Filter ? Blur ? Gaussian Blur). Уменьшите непрозрачность слоя и сотрите тень с угла ластиком.

Шаг 3

Повторите процесс и добавьте ещё одну тень на холм на отдельном слое.

Шаг 4

Давайте добавим немного реалистичности и удлиним дорогу. Перейдите на слой с дорогой и на маске белым цветом верните небольшой участок. Под дорогой нужно нарисовать тень на отдельном слое.

Шаг 5

Создайте новый слой для дороги. Инструментом Pencil Tool размером 1 пиксель нарисуйте неровности на дороге чёрным цветом. Создайте копию слоя и инвертируйте цвет линий (Ctrl + I). Сдвиньте копию на 1 пиксель и уменьшите непрозрачность.

Шаг 6

Улучшите свет и тени на ландшафте при помощи мягкой кисти с небольшой непрозрачностью.

Изометрические чертежи

Используйте изометрические чертежи, чтобы сделать свои схемы объемными. Можно создавать их с нуля либо использовать простые или трехмерные фигуры, а также шаблоны.

В этой статье:

Создание изометрического чертежа с нуля

1. В Visio, в меню Файл выберите пункт Новый, а затем щелкните Простой чертеж.

2. Выберите единицы измерения (метрические или американские), а затем нажмите кнопку Создать.

3. Откройте вкладку Вид и установите флажок Сетка в области Показать.

4. Откройте вкладку Главная и щелкните стрелку рядом с фигурой «Прямоугольник» в области Инструменты, а затем выберите Линия.

5. Нарисуйте фигуру вручную с помощью инструмента «Линия».

К началу страницы

Использование простых фигур

1. В Visio, в меню Файл выберите пункт Новый, а затем щелкните Простой чертеж.

2. Выберите единицы измерения (метрические или американские), а затем нажмите кнопку Создать.

3. Откройте вкладку Вид и установите флажок Сетка в области Показать.

4. Откройте вкладку Главная и выберите Дополнительные фигуры > Основные > Простые фигуры.

5. Перетащите фигуру из набора элементов Простые фигуры в область документа.

6. Выделите фигуру и щелкните точки соединения, чтобы изменить ее форму и размер.

   Совет: Для использования в другом месте рисунка может потребоваться точную копию фигуры. Нажмите CTRL+C, чтобы скопировать выбранную фигуру, и перетащите скопированную фигуру в сторону рисунка, пока не будете готовы к ее использованию.

7. Перетащите другие нужные фигуры из набора элементов Простые фигуры.

8. Откройте вкладку Главная и щелкните стрелку рядом с фигурой «Прямоугольник» в области Инструменты, а затем выберите Линия.

9. Нарисуйте линии вручную, чтобы дополнить фигуру.

10. Откройте вкладку Файл и выберите команду Параметры.

11. Выберите пункт Настроить ленту.

12. На экране Visio Параметры в области Основные вкладки, щелкните поле Разработчик .

13. Нажмите кнопку ОК.

    Совет: На ленте появится вкладка Visio Разработчик.

14. На вкладке Главная в группе Редактирование щелкните элемент Выделить и выберите команду Выделить все.

15. Откройте вкладку Разработчик.

16. В группе Конструктор фигур выберите элемент Операции, а затем — команду Обрезать.

17. Щелкните правой кнопкой мыши часть линии или фигуры, которую нужно удалить, а затем выберите команду Вырезать.

18. Повторяйте шаг 17, пока не доделаете чертеж или схему.

19. При необходимости удалите сетку, открыв вкладку Вид и сняв флажок Сетка в области Показать.

К началу страницы

Создание изометрического чертежа на основе шаблона

Инструкции ниже относятся к шаблону Трехмерная блок-диаграмма. Microsoft Visio несколько трехмерных шаблонов. Чтобы найти их, на вкладке Файл щелкните Создать, введите «трехмерная» или «объемная» в поле поиска и выберите шаблон, который лучше всего вам подходит:

• Блок-диаграмма

• Трехмерная маршрутная карта

• Трехмерная блок-диаграмма

• Схема рабочего процесса — объемная

• Подробная схема сети — объемная

• Принципиальная схема сети — объемная

К началу страницы

Использование шаблона «Трехмерная блок-диаграмма»

(Этот шаблон не доступен в Веб-приложение Visio. )

1. В Visio, в меню Файл выберите пункт > общиеи щелкните шаблон Блок-схема с перспективой.

2. Выберите единицы измерения (метрические или американские), а затем нажмите кнопку Создать.

3. Перетащите фигуру из набора элементов Трехмерные блоки на страницу документа.

4. Измените ориентацию, щелкнув и перетащив точку исчезновения (V.P.) в нужную область.

5. Дважды щелкните фигуру и введите текст.

6. Щелкните фигуру, щелкните Заливка в области Стили фигур и выберите цвет.

К началу страницы

Гексагональные тайловые миры / Хабр

Тайловость в играх – очень распространенное явление, особенно в играх инди сегмента. Чаще всего используют квадратные тайлы – в них проще всего задать необходимые данные, будь то карта уровня или инвентарь. Однако на квадратных и прямоугольных формах возможности подобной системы не ограничиваются.

В топовых играх конца девяностых — начала нулевых часто можно увидеть шестиугольную сетку заместо квадратной – в то время это смотрелось очень интересно, в особенности в сочетании с изометрией. Именно о работе с такими сетками и пойдет речь.

Если вы не читали мою предыдущую статью про прямоугольные сетки, то рекомендую ознакомится, потому как я иногда буду опускать некоторые вещи, ссылаясь именно на нее. Дабы не изобретать велосипед, некоторые алгоритмы я взял с этой статьи на английском. Кто не хочет или не может в английский, есть ее перевод на хабре. Все демки и примеры сделаны на движке Godot Engine v 3.2.3 с использованием его встроенного языка.

Думаю в целом его синтаксис ясен, однако оставлю ссылки на некоторые функции:

Система координат

На протяжении всей статьи мы будем работать только с правильными шестиугольниками, у них все стороны равны.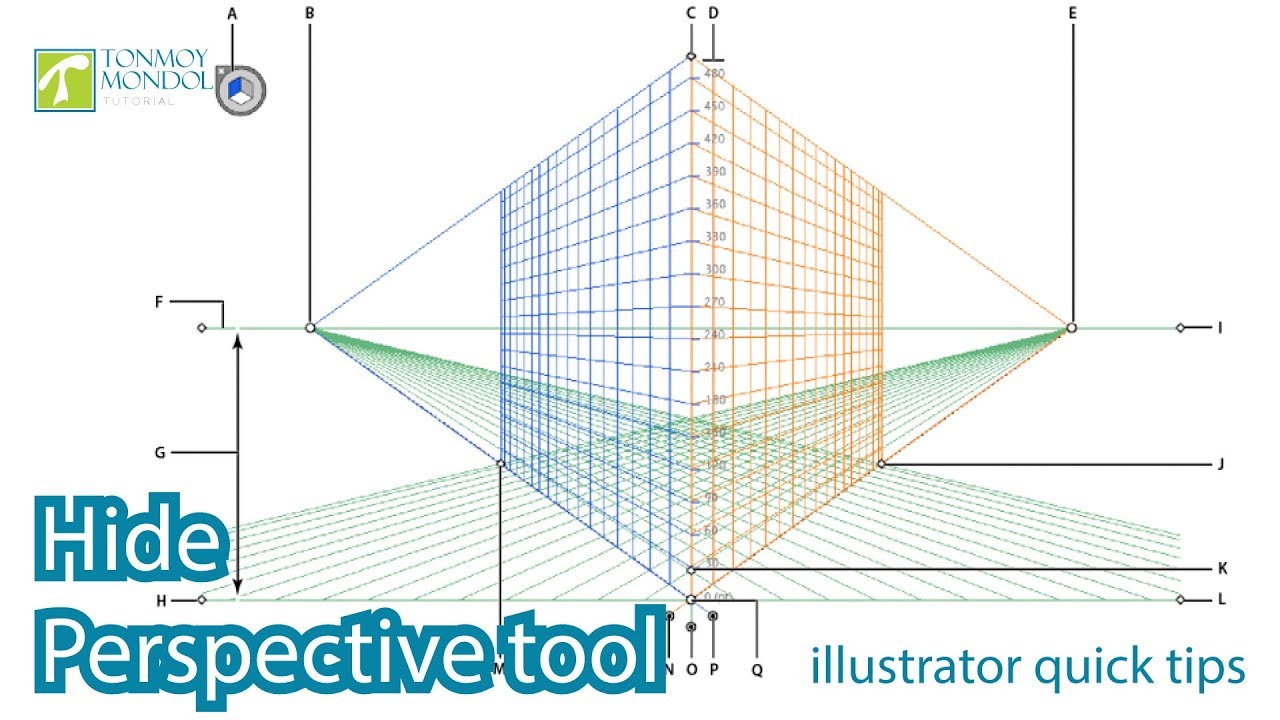 Работа с неправильными шестиугольниками лишена смысла в принципе. Если не брать всякие повороты и искажения, существует два вида шестиугольных сеток, вертикально и горизонтально ориентированных:

• Такие я буду называть вертикальными (у ячейки есть явный вертикальный сосед):

• А такие горизонтальными (у ячейки есть явный горизонтальный сосед):

Уже на этапе введения координат могут возникнуть проблемы. Дело в том, что в шестиугольной сетке невозможно ввести типичную декартову систему координат — всегда будет ось, вдоль которой у ячейки не будет явного соседа. На самом деле существует огромное количество систем координат для таких сеток. Более подробно о них рассказано в упомянутых вначале статьях. Я рассказывать про каждую не буду, все таки пост больше про использование сеток, а не их исследование.

Пожалуй первое, что приходит в голову, это таки впихнуть декартовы оси, однако для этого по одному из направлений координаты придется смещать:

Такая система называется координатами смещения.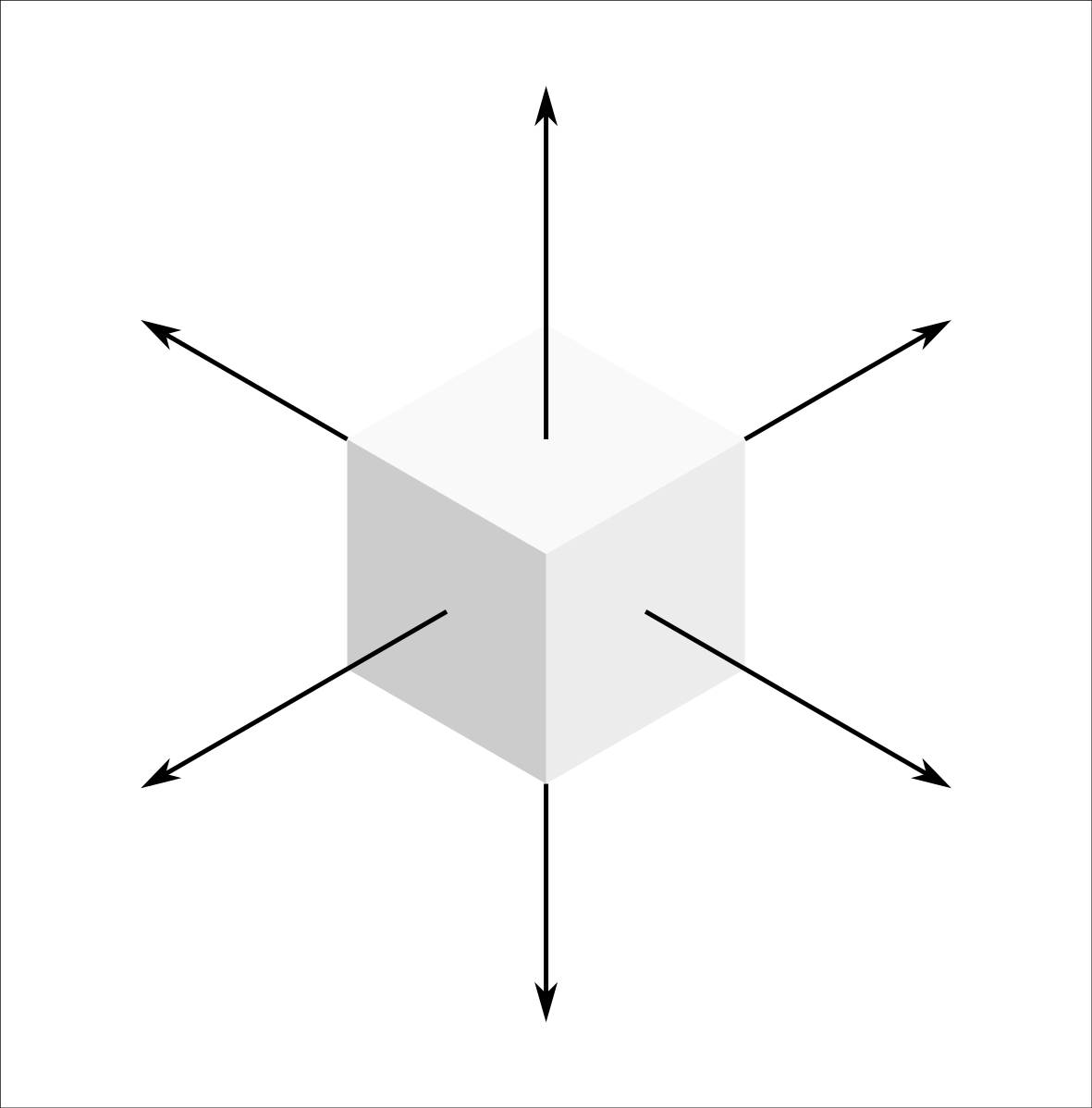 Бывает два вида координат смещения — четные и нечетные. Они отличаются лишь выбором соседа для смещения. В моем примере использованы нечетные координаты смещения, т.е. ячейка смещается к нижней в случае вертикальной ориентации или к правой в случае горизонтальной.

Главная проблема этих координат состоит в выборе базисов. Для разных ячеек базис к следующей ячейке может отличаться от того, по которому мы к ней перешли. Если вы помните из статьи про прямоугольные тайлы, там мы обращали матрицу из базисных векторов и умножали на нее радиус-вектор пикселя, получая координаты ячейки. Здесь так не выйдет, провернув тоже самое мы просто получим квадратную сетку.

Вообще у сетки шестиугольников есть три ярко выраженных оси:

Что-то напоминает, не находите? Тут три оси, прям как в пространстве. На самом деле гений тот человек — кто не просто увидел, что если взглянуть на куб под определенным углом, то получится шестиугольник, а еще и додумался использовать трехмерные координаты в двумерной сетке шестиугольников. Правда вот попробовав посчитать координаты на двумерной сетке, могут вскипеть мозги, ведь третья ось тут кажется лишней и ее использование будто только мешает. Для разрешения данной ситуации просто посмотрим откуда взялись кубы:

Для получения сетки шестиугольников надо взглянуть в изометрии на пирамидку, на каждом уменьшении высоты которой увеличивается количество кубиков в ряду на один. Включив фантазию, можно увидеть в каждом кубе шестиугольник. Включив внимательность, можно увидеть в левом нижнем углу координаты. Включив логику, можно увидеть, что сумма этих самых координат всегда равна некоторому числу, которое, кстати говоря, может быть любым, ведь мы сами решаем, откуда начнется система координат. В моем случае это 15, просто потому, что система отсчета в этом редакторе начинается с нижнего дальнего угла (в случае изометрического вида). Нам незачем таскать за собой лишнюю константу, поэтому возьмем ее за ноль. Таким образом, сумма трех координат всегда и везде равна нулю, поэтому третья нам попросту не нужна, ведь мы можем получить ее из двух других. Теперь и получается, что «мешающая» третья ось уходит. Наконец то мы можем спокойно направить базисы и у каждой ячейки всегда будет точный сосед, находящийся вдоль оси:

Т.к. у шестиугольника нет левого верхнего угла, мы можем поместить начало координат по сути в любую точку. Самым оптимальным мне показался центр фигуры, ведь относительно него она симметрична.

Преобразование координат

Пожалуй это то, на чем запарываются многие при попытке сделать нечто шестиугольное. Я слышал множество способов, порой они были очень забавные. Например, мне больше всего запомнился способ, где предлагалось сделать невидимую маску с такой же сеткой, где каждая ячейка окрашена в свой цвет, а каждому цвету соответствуют координаты. При смещении курсора смотрим в маску и по цвету определяем координаты. Сложно, с костылями, но работать может. А если мы захотим другой размер? Перерисовывать? Вы тут явно не за этим.

Вообще работать с шестиугольниками неудобно, ведь пиксели то квадратные, поэтому лучше все как то привести к прямоугольникам, что бы можно было использовать типичные матричные преобразования. Для этого найдем диагонали шестиугольника (а — сторона):

Оранжевые (маленькие) диагонали делятся пополам зелеными (большими), а зеленые оранжевыми, если последние провести из середины стороны. Уже получается, что мы можем разделить шестиугольник на 4 прямоугольника. Однако некоторые вершины в таком случае будут лежать где то между углами сетки, а ведь нам хотелось бы, чтобы все они попадали ровно в углы. На самом деле «где то», это ровно по серединке, поэтому разделим большие ячейки еще на пополам, тогда все вершины шестиугольника будут ложиться точно в углы прямоугольной сетки:

Желтую сетку в дальнейшем я буду называть вспомогательной. Для задания ее базисов будем использовать такие значения:

# Для горизонтальных шестиугольников
var hex_size = 32

var short = int(size*sqrt(3)/2) # 1/2 from short hex diagonal
var long = int(size/2) # 1/4 from long hex diagonal

Теперь мы можем выразить базисы шестиугольной сетки, используя базисы вспомогательной сетки:

Запишем все базисы в коде:

...

# Transorm2D в godot - это матрица 3x2, где последняя строка указыает
# смещение объекта, в дальнейшем она не будет использоваться совсем, 
# поэтому считайте это просто матрицей 2x2. Сделано это для удобства,
# на объяснения никак не повлияет.
# У нее есть два атрибута - x и y. Каждый из них это вектор. X - представляет
# первый столбец матрицы 2x2 (крайняя строка не учитывается), Y - второй столбец.
  
var grid_basis = Transform2D() # Матрица базисов вспомогательной сетки
var hex_basis = Transform2D() # Матрица базисов гексагональной сетки

...
  
# Для вертикальной сетки
grid_basis.x = Vector2(long, 0)
grid_basis.y = Vector2(0, short)

hex_basis.x = grid_basis.x*3 + grid_basis.y
hex_basis.y = grid_basis.y*2

# Для горизонтальной сетки
grid_basis.x = Vector2(short, 0)
grid_basis.y = Vector2(0, long)
			
hex_basis.x = grid_basis.x*2
hex_basis.y = grid_basis.x+grid_basis.y*3

Я пользуюсь именно встроенными средствами Godot для упрощения работы в целом. Все подобные места будут поясняться в общем виде, как бы это делалось без встроенных возможностей.

Шестиугольник в пиксель

Вот за что я люблю математику, так это за то, что если она работает, то работает везде. Так что для получения центра шестиугольника в пикселях из его координат на сетке надо просто умножить базисы на координаты:

func hex2pixel(hex):
	return hex.x*hex_basis.x + hex.y*hex_basis.y

Для получения каждой вершины просто прибавляем по нужным базисам:

Тогда для получения вершины в коде прибавляем нужный вектор (см. картинку выше) к центру шестиугольника. Я написал только функцию получения массива вершин, ибо по отдельности они почти никогда не нужны.

Для вертикальных шестиугольников:

func _get_vert_hex_vertices(hex):
	var pixel = hex2pixel(hex)
	return PoolVector2Array([
		pixel+2*grid_basis.x,
		pixel+grid_basis.x+grid_basis.y,
		pixel-grid_basis.x+grid_basis.y,
		pixel-2*grid_basis.x,
		pixel-grid_basis.x-grid_basis.y,
		pixel+grid_basis.x-grid_basis.y
	])

Для горизонтальных шестиугольников:

func _get_hor_hex_vertices(hex):
	var pixel = hex2pixel(hex)
	return PoolVector2Array([
		pixel+grid_basis.x-grid_basis.y,
		pixel+grid_basis.x+grid_basis.y,
		pixel+2*grid_basis.y,
		pixel-grid_basis.x+grid_basis.y,
		pixel-grid_basis.x-grid_basis.y,
		pixel-2*grid_basis.y,
	])

Пиксель в шестиугольник

Наверно самая интригующая часть поста. На самом деле ничего нового почти не будет, ведь для получения вещественных координат ячейки все также обращаем матрицу и умножаем на нее радиус-вектор пикселя:

Для горизонтальной ориентации

В коде это записывается так:

func pixel2hex(pixel):
	var x = pixel.x/(2*cw) - pixel.y/(6*ch)
	var y = pixel.y/(3*ch)
	return round_hex(Vector2(x, y))

Для вертикальной ориентации

В коде это записывается так:

func pixel2hex(pixel):
	var x = pixel.x/(3*cw)
	var y = pixel.y/(2*ch) - pixel.x/(6*cw)
	return round_hex(Vector2(x, y))

Однако я буду пользоваться функцией affine_inverse у Transform2D, для того, что бы при изменении базисных векторов постоянно не менять функции преобразований, позже увидите зачем это надо. Вы скорее всего работаете в другой среде (и зря), поэтому вам придется писать обращение матрицы самостоятельно. Кто не знает как это делается, или забыл, может почитать тут, или переписать следующие функции в свой язык:

Функции

func invert_basis(basis:Transform2D): # обращение матрицы
	var det = basis.x.x*basis.y.y - basis.y.x*basis.x.y
	var idet = 1.0/det
	# Я не уверен что Transform2D передается по значению, по этому
	# копирую данные в новый объект
	var res = basis
	res.y.y = basis.x.x*idet
	res.x.x = basis.y.y*idet
	res.x.y = -basis.x.y*idet
	res.y.x = -basis.y.x*idet
	return res
	
func vec_mul_basis(vec:Vector2, basis:Transform2D): # умножение вектора на матрицу
	var x = vec.x*basis.x.x + vec.y*basis.y.x
	var y = vec.x*basis.x.y + vec.y*basis.y.y
	return Vector2(x, y)
	
func pixel2hex(pixel):
	return round_hex(vec_mul_basis(pixel, invert_basis(hex_basis)))

Средствами Godot это можно записать всего в одну строчку:

func pixel2hex(pixel):
	return round_hex(hex_basis.affine_inverse().xform(pixel))

Тут .xform(Vector2) — это метод для умножения матрицы на переданный в него вектор, аналог vec_mul_basis из моего кода. Такой код работает для обеих ориентаций.

Если вы хотя бы бегло прочитали вышеприведенный код, то наверняка заметили функцию round_hex вместо типичных приведений к int. Дело в том, что полных координат у шестиугольника 3, и они обладают условием x + y + z = 0, а после округления каждой из них равенство может нарушиться. Поэтому необходимо задать координату с наибольшей ошибкой округления через две другие, тогда условие выполнится. Да, данный метод полностью слизан отсюда, однако зачем придумывать велосипед, если можно взять готовый? Так же тут используется именно round, а не приведение к int, ведь основание каждой ячейки находится в ее центре, а не в левом верхнем углу, как в случае с прямоугольными сетками:

func round_hex(hex:Vector2):
	var rx = round(hex.x)
	var ry = round(hex.y)
	var rz = round(-hex.x-hex.y) # z = -x-y
	
	var x_diff = abs(hex.x-rx) # Ошибка округления x
	var y_diff = abs(hex.y-ry) # Ошибка округления y
	var z_diff = abs(-hex.x-hex.y-rz) # Ошибка округления z
	if x_diff > y_diff and x_diff > z_diff:
		rx = -ry-rz # Приведение под равенство
	elif y_diff > z_diff:
		ry = -rx-rz # Приведение под равенство
	return Vector2(rx, ry)

Работает все замечательно:

Вертикальная ориентацияГоризонтальная ориентация

Однако я надеюсь вы не думаете, что сетки, это вручную нарисованные текстуры. Я не самоубийца.

Рисование сеток

Все примеры и объяснения я буду приводить на горизонтальной сетке, ведь для вертикальной они аналогичны. Для рисования последних я просто оставлю готовую функцию.

Для рисования сетки необходимо знать ее размеры. Размеры шестиугольной сетки будем задавать в координатах смещения, так просто понятнее. Тогда по горизонтали будет в два раза больше ячеек вспомогательной сетки, чем шестиугольников, ведь по горизонтали у шестиугольника 2 ячейки. Для нахождения вертикальных размеров заметим, что для перехода к нижнему шестиугольнику мы вниз проходим три вертикальных базиса, однако для крайнего шестиугольника соседа снизу нет, поэтому самая нижняя чать остается неучтенной, так что нужно прибавить единицу:

const hex_map_size = Vector2(7, 7) # размер сетки шестиугольников
var grid_map_size:Vector2 # размер вспомогательной сетки
...
grid_map_size.x = hex_map_size.x*2
grid_map_size.y = hex_map_size.y*3+1

Для вертикальных шестиугольников все аналогично, только формулы для вычисления ширины и высоты меняются местами:

...
grid_map_size.x = hex_map_size.x*3+1
grid_map_size.y = hex_map_size.y*2

Сетку из шестиугольников можно разбить на две части, на вертикальные линии и на паттерн вершин:

Будем рисовать каждую составляющую по отдельности. Начнем с вертикальных линий. Можно заметить, что в каждом ряду линии рисуются с интервалом в 2 ячейки, а каждый четный по счету ряд начинается со второй, а не с первой ячейки. Также увидим то, что первый ряд начинается со со смещением в одну ячейку относительно верхей границы, а ряды разделяет одна ячейка. С учетом того, что длина штриха в две ячейки, между верхними концами отрезков находятся три ячейки. Тогда в цикле начинаем с единицы и идем до нижнего края карты с шагом 3, а во втором цикле начинаем со столбца, индекс которого обратен четности ряда, проще говоря 1-i%2, и идем до правого края карты, но на единицу больше, чтобы нарисовать таки крайние линии, с шагом в две ячейки. В кадой итерации второго цикла просто рисуем отрезок высотой две ячейки:

for i in range(1, grid_map_size.y, 3):
	for j in range(1-i%2, grid_map_size.x+1, 2):
		VisualServer.canvas_item_add_line(surf, grid_basis.x*j+grid_basis.y*i, grid_basis.x*j+grid_basis.y*(i+2), color, width, antialiasing)

Этот код будет рисовать только вертикальные линии. Теперь нужно нарисовать паттерн вершин. Есть всего два вида наклонных линий, от нижнего левого угла к верхнему правому (их я буду называть нижними диагоналями), или от верхнего левого к нижнему правому (их я буду называть верхними диагоналями), причем в одной строке они чередуются, а в следующей строке паттерн меняет четность. Четным я буду называть паттерн, начинающийся с нижней диагонали, нечетным — начинающийся в верхней диагонали.

Каждые две строки паттерна разделяют две ячейки, поэтому чтобы перейти от одной к следующей, необходимо сдвинуться на 3 строки вниз. Как я уже говорил, каждую строку паттерн меняет четность, и так совпало, что при переходе к следующей строке ее индекс тоже меняет четность.

Для рисования паттернов пробегаем каждую третью строку, начиная с нулевой, а в каждой строке пробегаемся по столбцам. Тогда для выбора нужной линии сравниваем четности строки и столбца, если они совпадают, то рисуем нижнюю диагональ, иначе верхнюю. Тут я считаю нужным показать, как задается каждый угол ячейки с координатами {j, i} , где j — столбец (как бы x), i — строка (как бы y). Размер ячейки увеличен только для демонстрации:

В коде этот алгоритм выглядит так:

# Drawing vertices
for i in range(0, grid_map_size.y, 3): # рисуем на каждой третьей строке
	for j in range(grid_map_size.x): # крайний столбец не захватываем, т.к. в коде прибавляется единица
		if i%2 == j%2: # нижняя диагональ
			VisualServer.canvas_item_add_line(surf, grid_basis.x*j+grid_basis.y*(i+1), grid_basis.x*(j+1)+grid_basis.y*i, color, width, antialiasing)
		else: # верхняя диагональ
			VisualServer.canvas_item_add_line(surf, grid_basis.x*j+grid_basis.y*i-offset, grid_basis.x*(j+1)+grid_basis.y*(i+1), color, width, antialiasing)

Однако просто нарисовав на холсте сетку, получатся непонятки с координатами:

Дело все в том, что начало координат находится в центре шестиугольника, а начинаем рисовать мы с левого верхнего угла вспомогательной сетки, также как мы это делали с обычными сетками. Для рисования сетки правильно, т.е. из начала координат, необходимо сдвинуть рисование на одну ячейку влево и на две вверх, ведь именно под таким смещением находится начало координат.

Однако и на этом не все. Если просто объеденить весь код выше в одну функцию, то при четных высотах она будет рисовать ненужные хвосты:

Эти хвосты рисуются прямо в углах вспомогательной сетки, поэтому просто добавим условие, что мы в них не находимся, иначе просто не рисуем тут диагональ.

Соединив все вместе, получим такую функцию:

func _draw_hor_rect_grid(surf:RID, color:Color, width=1.0, antialiasing=false):
	var offset = grid_basis.x+grid_basis.y*2
	# Drawing vertical lines
	for i in range(1, grid_map_size.y, 3):
		for j in range(1-i%2, grid_map_size.x+1, 2):
			VisualServer.canvas_item_add_line(surf, grid_basis.x*j+grid_basis.y*i-offset, grid_basis.x*j+grid_basis.y*(i+2)-offset, color, width, antialiasing)

	# Drawing vertices
	for i in range(0, grid_map_size.y, 3):
		for j in range(grid_map_size.x):
			if int(hex_map_size.y)%2 == 1 or not (i == grid_map_size.y-1 and (j == 0 or j == grid_map_size.x-1)):
				if i%2 == j%2:
					VisualServer.canvas_item_add_line(surf, grid_basis.x*j+grid_basis.y*(i+1)-offset, grid_basis.x*(j+1)+grid_basis.y*i-offset, color, width, antialiasing)
				else:
					VisualServer.canvas_item_add_line(surf, grid_basis.x*j+grid_basis.y*i-offset, grid_basis.x*(j+1)+grid_basis.y*(i+1)-offset, color, width, antialiasing)

При рисовании вспомогательной сетки кстати тоже используем смещение. На всякий случай оставлю тут и ее рисование, хотя это есть в моей статье про прямоугольные сетки:

func draw_auxiliary_grid(surf:RID, color:Color, width=1.0, antialiasing=false):
	var offset = grid_basis.x+grid_basis.y*2
	for i in grid_map_size.x+1:
		Canvas.line(surf, grid_basis.x*i-offset, grid_basis.x*i+grid_basis.y*grid_map_size.y-offset, color, width, antialiasing)
	for i in grid_map_size.y+1:
		Canvas.line(surf, grid_basis.y*i-offset, grid_basis.x*grid_map_size.x+grid_basis.y*i-offset, color, width, antialiasing)

И, как и обещал, функция для рисования вертикально-ориентированной сетки:

func _draw_vert_rect_grid(surf:RID, color:Color, width=1.0, antialiasing=false):
	var offset = grid_basis.x*2+grid_basis.y
	# Drawing horizontal lines
	for i in range(1, grid_map_size.x, 3):
		for j in range(1-i%2, grid_map_size.y+1, 2):
			VisualServer.canvas_item_add_line(surf, grid_basis.x*i+grid_basis.y*j-offset, grid_basis.x*(i+2)+grid_basis.y*j-offset, color, width, antialiasing)
			
	# Drawing vertices
	for i in range(0, grid_map_size.x, 3):
		for j in range(grid_map_size.y):
			if int(hex_map_size.x)%2 == 1 or not(i == grid_map_size.x-1 and (j == 0 or j == grid_map_size.y-1)):
				if j%2 == i%2:
					VisualServer.canvas_item_add_line(surf, grid_basis.x*(i+1)+grid_basis.y*j-offset, grid_basis.x*i+grid_basis.y*(j+1)-offset, color, width, antialiasing)
				else:
					VisualServer.canvas_item_add_line(surf, grid_basis.x*i+grid_basis.y*j-offset, grid_basis.x*(i+1)+grid_basis.y*(j+1)-offset, color, width, antialiasing)

Результат вполне неплох, нигде линии не рисуются дважды (сетка рисовалась немного прозрачной на черном фоне, а яркость линий везде одинакова):

Сетка вертикальных шестиугольниковСетка горизонтальных шестиугольников

Однако рендерить такие сетки в реальном времени довольно затратно, тут рисуется множество отдельных отрезков, что сильно замедляет работу. Просто для примера, пустое черно окно у меня имеет fps около 950, а при рисовании белым цветом Color8(255, 255, 255, 200) шестиугольной сетки размера 10×10 и размером шестиугольнкиа 32 пикселя, fps примерно 260. Так что рисовать сетки процедурно резонно только на начальном этапе разработки, потом лучше отрендерить ее заранее и использовать как текстуру.

Рисование шестиугольной сетки шестиугольников

Сетки шестиугольников конечно здорово, но иногда хочется чего то большего. Например больше шестиугольников, поэтому сделаем большой шестиугольник из маленьких. Такая сетка может пригодиться, если мы, например, делаем шестиугольные шахматы.

Рисование этой сетки лишь немного сложнее рисования обычной, хотя на первый взгляд мой код похож на код сатаны. Поробую объяснить что откуда взялось. Результат будет примерно таков:

Для начала нам конечно же нужны размеры сеток. Т.к. мы рисуем сетку в виде правильного шестиугольника, ее размер можно задать одним значением. В коде я использую тип Vector2 только для совмещения этой переменной с прямоугольнйо сеткой, при рисовании будет использоваться только X координата. Тогда для задания размеров вспомогательной сетки нужно найти диагональ большого шестиугольника. Для этого вспомним, что бОльшая диагональ шестиугольника в два раза больше его стороны. В нашем случае шестиугольник состоит из маленьких таких же. В таком случае центр будет учитываться два раза, поэтому вычтем единицу:

var hex_map_size = Vector2(5, <не имеет значения>)
...
var diagonal = hex_map_size.x*2-1

Размеры вспомогательной сетки задаются аналогично тому, что мы делали ранее. Для горизонтальной ориентации ширина будет в два раза больше диагонали, а высота в три раза и еще на единицу больше:

...
grid_map_size.x = diagonal*2
grid_map_size.y = diagonal*3+1

Для вертикальных значения меняются местами:

grid_map_size.x = diagonal*3+1
grid_map_size.y = diagonal*2

Шестиугольную сетку можно точно также разбить на две части, на паттерн вершин и вертикальные линии:

Начнем с рисования вершин. Рисовать каждый слой по-отдельности не имеет смысла, ведь фигура симметрична. Мы можем разделить всю вспомогательную сетку на четыре части и, нарисовав одну четверть, отобразить ее зеркально на все остальные. Сетка кстати всегда будет делиться ровно, и вот почему. По горизонтали понятно, ведь в формуле ширины мы удваиваем диагональ шестиугольной карты. А эта самая диагональ будет всегда нечетна, ведь мы от четного числа отнимаем единицу (hex_map_size.x*2-1). В формуле высоты вспомогательной сетки мы умножаем эту диагональ на 3, и результат получится тоже нечетным, а после прибавления единицы все выражение становится четным. Таким образом ширина и высота вспомогательной сетки всегда четны, и как следствие, ее можно всегда разделить на четыре одинаковые части:

Тогда мы можем пробегать в циклах только до половин размеров вспомогательной сетки, а для рисования в других частях будем просто отражать точки рисования.

При такой форме сетки рисование вершин начинается не с самой левой колонки и паттерн всегда четный (при рассмотрении одной четверти). При увеличении размера сетки на единицу, первый шестиугольник в самом верхем ряду сдвигается на одну ячейку вспомогательной сетки, т.к. мы увеличиваем в том числе и размер левой грани, в которой под каждым шестиугольником следующий находится не только ниже, но и левее на половину шестиугольника, т.е. на одну ячейку. Тогда каждый следующий паттерн начинает рисоватся на ячейку ближе к левому краю, а самый первый ряд имеет смещение на единицу меньшее, чем размер шестиугольной карты, т.к. первый шестиугольник в нем тоже является частью левой грани, так что под ним шестиугольников меньше на эту самую единицу, чем размер карты.

Также вспомним, что каждый следующий паттерн рисуется со смещением в три ячейки от предыдущего, поэтому в цикле идем от нуля до половины высоты вспомогательной сетки с шагом в три, попутно вычисляя смещение для каждого ряда:

for i in range(0, grid_map_size.y/2, 3): # Drawing vertices
  # тут i/3 потому что мы идем со смещением 3, а при расчетах нужен индекс
  start = hex_map_size.x-1 - i/3  

Проходить по ширине будем также до середины вспомогательной сетки, начиная с высчитанного ранее смещения:

for i in range(0, grid_map_size.y/2, 3): # Drawing vertices
  # тут i/3 потому что мы идем со смещением 3, у при расчетах нужен индекс паттерна
  start = hex_map_size.x-1 - i/3  
  for j in range(start, grid_map_size.x/2):
  	pass # Пока ничего не делаем

Каждый паттерн при рисовании шестиугольной карты четный, а вот смещение чередует свою четность. Четность начального смещения напрямую зависит от четности размера карты — они противоположны. Двигаясь вниз по рядам паттерна, индекс ряда меняет четность, как и смещение для этого ряда. Если помните, для выбора диагонали при рисовании прямоугольной сетки мы сравнивали четность ряда и колонки. Тут же меняются обе четности, и при разных размерах карты они будут то совпадать при начальных значениях, то нет.

Приведу пример. Мы рисуем нижнюю диагональ, если индексы ряда и колонки совпадают, иначе верхнюю. Поставим размер карты 5. Тогда начальное смещение будет четным, как и индекс первого ряда (i=0). Исходя из условия, рисуем нижнюю диагональ, как и должно быть. Однако поставив четный размер, скажем, 4, начальное смещение будет нечетным, а вот индекс первого ряда по прежнему четным. Тогда взглянув на условие компьютер выберет верхюю диагональ, а ведь нам все еще для начала нужна нижняя. Вот как это будет выглядеть:

Тут на самом деле всего лишь надо поменять четность паттерна, тогда все встанет на свои места. Получается, выбор условия рисования нижней диагонали зависит от четности самого размера карты. Тут можно заметить, что разница четностей столбца и ряда в каждой первой диагонали ряда паттерна обратна четности размера карты. А при рисовании паттерна диагонали просто чередуются, как и чередуется четность столбца, и как следствие чередуется равенство разностей четностей ряда и столбца и четности размера карты. Поэтому для выбора диагонали используем равентво abs(i%2 - j%2) != parity, где parity — это остаток от деления размера карты на два. Если это условие верно, рисуем нижнюю диагональ, иначе верхнюю. Получим то что нужно, осталось отразить по красным линиям:

Код рисования четверти всего паттерна

func _draw_hor_hex_grid(surf:RID, color:Color):	
	var parity = int(hex_map_size.x)%2
	var start
	for i in range(0, grid_map_size.y/2, 3): # Drawing vertices
		start = hex_map_size.x - i/3 - 1
		for j in range(start, grid_map_size.x/2):
			if abs(i%2 - j%2) != parity:
				# Down diagonal
				VisualServer.canvas_item_add_line(surf, grid_basis.x*j+grid_basis.y*(i+1), grid_basis.x*(j+1)+grid_basis.y*i, color)
      else:
				# Top diagonal
				VisualServer.canvas_item_add_line(surf, grid_basis.x*(j)+grid_basis.y*(i), grid_basis.x*(j+1)+grid_basis.y*(i+1), color)

Для отражения точек рисования отнимаем от края вспомогательной сетки индекс точки, ничего сложного. А вот в коде это выглядит громоздко. Взгляните сами:

func _draw_hor_hex_grid(surf:RID, color:Color, width=1.0, antialiasing=false):
	var parity = int(hex_map_size.x)%2
	var start
	for i in range(0, grid_map_size.y/2, 3): # Drawing vertices
		start = hex_map_size.x - i/3 - 1
		for j in range(start, grid_map_size.x/2):
			if abs(i%2 - j%2) != parity:
				# Down diagonal
				VisualServer.canvas_item_add_line(surf, grid_basis.x*j+grid_basis.y*(i+1), grid_basis.x*(j+1)+grid_basis.y*i, color)
				VisualServer.canvas_item_add_line(surf, grid_basis.x*(grid_map_size.x-j)+grid_basis.y*(i+1), grid_basis.x*(grid_map_size.x-j-1)+grid_basis.y*i, color)

				VisualServer.canvas_item_add_line(surf, grid_basis.x*j+grid_basis.y*(grid_map_size.y-i-1), grid_basis.x*(j+1)+grid_basis.y*(grid_map_size.y-i), color)
				VisualServer.canvas_item_add_line(surf, grid_basis.x*(grid_map_size.x-j)+grid_basis.y*(grid_map_size.y-i-1), grid_basis.x*(grid_map_size.x-j-1)+grid_basis.y*(grid_map_size.y-i), color)
			else:
				# Top diagonal
				VisualServer.canvas_item_add_line(surf, grid_basis.x*(j)+grid_basis.y*(i), grid_basis.x*(j+1)+grid_basis.y*(i+1), color)
				VisualServer.canvas_item_add_line(surf, grid_basis.x*(grid_map_size.x-j)+grid_basis.y*(i), grid_basis.x*(grid_map_size.x-j-1)+grid_basis.y*(i+1), color)

				VisualServer.canvas_item_add_line(surf, grid_basis.x*(j)+grid_basis.y*(grid_map_size.y-i), grid_basis.x*(j+1)+grid_basis.y*(grid_map_size.y-i-1), color)
				VisualServer.ca

Но ничего страшного, ковид пережили — переживем и это. Зато получаем правильный паттерн для сеток с четными и нечетным размером:

Если вы что-то поняли во всей этой мешанине четностей, то либо вы гений, либо у меня получилось что-то объяснить. Однако дальше не легче, но радует то, что мы почти нарисовали сетку. Осталось добавить вертикальные линии — это будет финальным штрихом в нашей картине.

Тут я не стал ничего придумывать с отражениями, ведь отрезки рисуются в две ячейки и при отражении некоторые места будут рисоваться два раза, а обрабатывать кучу исключений отдельно не очень хочется. Самым простым решение мне показалось рисовать вертикальные линии также, как мы это делали с прямоугольной сеткой, только отбрасывать линии в углах. Напомню код рисования линий в простой прямоугольной сетке:

for i in range(1, grid_map_size.y, 3):
	for j in range(1-i%2, grid_map_size.x+1, 2):
		VisualServer.canvas_item_add_line(surf, grid_basis.x*j+grid_basis.y*i, grid_basis.x*j+grid_basis.y*(i+2), color, width, antialiasing)

Однако просто скопипастив его в нашу функцию, получим кривое рисование при четных размерах карты, ведь при них первый ряд должен иметь смещение в единицу, а при нечетных этого смещения быть не должно. Это вытекает из смещения первого шестиугольника в первом ряду, при четных значения оно нечетно поэтому и рисуем со смещением, и наоборот. Для выбора смещения сравним четности размера карты и ряда, если они отличаются, то рисуем без смещения, иначе со смещением. Пихать сюда условие не имеет смысла, ведь мы можем выбрать смещение через отличие четности карты и четности столбца конструкцией abs(parity-i%2). Просто напомню — parity это остаток от деления размера карты на два. Проверьте сами, при четных столбцах и нечетных размерах карты получается единица — то самое смещение. Запишем это выражение в смещение в цикле:

for i in range(1, grid_map_size.y, 3):
	for j in range(abs(parity-i%2), grid_map_size.x+1, 2):
		VisualServer.canvas_item_add_line(surf, grid_basis.x*j+grid_basis.y*i, grid_basis.x*j+grid_basis.y*(i+2), color, width, antialiasing)

Цель почти достигнута, осталось избавиться от лишних линий по углам:

Для этого при рисовании линий добавим некоторое условие, что мы хотим нарисовать линию в пределах каких-то границ. Для обозначения границ заметим, что с каждым рядом мы начинаем рисовать на ячейку ближе к левой границе, поэтому границу можно задать как смещение первого ряда минус индекс ряда:

...
start = hex_map_size.x-1 - i/3

Однако в нижней половине шестиугольника смещение начинает идти обратно, а индекс ряда только возрастает. Поэтому будем смотреть, в какой половине мы находимся, и выбирать нужную формулу для расчета левой границы. Для нижней части карты используем положение ряда относительно центра карты, просто отняв от его индекса половину ее размера:

...
start = (i-grid_map_size.y/2)/3

Это мы задали левые границы. Для правых просто отразим левые в силу четности размеров вспомогательной сетки:

for i in range(1, grid_map_size.y, 3):
	if i <= grid_map_size.y/2:
		start = hex_map_size.x-1 - i/3
	else:
		start = (i-grid_map_size.y/2)/3

	for j in range(abs(parity-i%2), grid_map_size.x+1, 2):
		if j >= start and j <= grid_map_size.x-start: # избавляемся от лишних линий
			VisualServer.canvas_item_add_line(surf, grid_basis.x*j+grid_basis.y*i, grid_basis.x*j+grid_basis.y*(i+2), color, width, antialiasing)

Вот и все — сетка готова. Осталось только добавить смещение для расположения сетки в начало координат, offset = grid_basis.x+grid_basis.y*2. Однако тут опять играет роль четность размера карты, так что когда она четна прибавляем к смещению горизонтальный базис ячейки.

После всего этого мы наконец может расслабиться и посмотреть на точнейшим образом нарисованные сетки:

Горизонтальная ориентация

func _draw_hor_hex_grid(surf:RID, color:Color, width=1.0, antialiasing=false):
	var parity = int(hex_map_size.x)%2
	var offset = grid_basis.x+grid_basis.y*2 + grid_basis.x*(1-parity)
	var start
	for i in range(0, grid_map_size.y/2, 3): # Drawing vertices
		start = hex_map_size.x - i/3 - 1
		for j in range(start, grid_map_size.x/2):
			if abs(i%2 - j%2) != parity:
				# Down diagonal
				VisualServer.canvas_item_add_line(surf, grid_basis.x*j+grid_basis.y*(i+1)-offset, grid_basis.x*(j+1)+grid_basis.y*i-offset, color)
				VisualServer.canvas_item_add_line(surf, grid_basis.x*(grid_map_size.x-j)+grid_basis.y*(i+1)-offset, grid_basis.x*(grid_map_size.x-j-1)+grid_basis.y*i-offset, color)

				VisualServer.canvas_item_add_line(surf, grid_basis.x*j+grid_basis.y*(grid_map_size.y-i-1)-offset, grid_basis.x*(j+1)+grid_basis.y*(grid_map_size.y-i)-offset, color)
				VisualServer.canvas_item_add_line(surf, grid_basis.x*(grid_map_size.x-j)+grid_basis.y*(grid_map_size.y-i-1)-offset, grid_basis.x*(grid_map_size.x-j-1)+grid_basis.y*(grid_map_size.y-i)-offset, color)
			else:
				# Top diagonal
				VisualServer.canvas_item_add_line(surf, grid_basis.x*(j)+grid_basis.y*(i)-offset, grid_basis.x*(j+1)+grid_basis.y*(i+1)-offset, color)
				VisualServer.canvas_item_add_line(surf, grid_basis.x*(grid_map_size.x-j)+grid_basis.y*(i)-offset, grid_basis.x*(grid_map_size.x-j-1)+grid_basis.y*(i+1)-offset, color)

				VisualServer.canvas_item_add_line(surf, grid_basis.x*(j)+grid_basis.y*(grid_map_size.y-i)-offset, grid_basis.x*(j+1)+grid_basis.y*(grid_map_size.y-i-1)-offset, color)
				VisualServer.canvas_item_add_line(surf, grid_basis.x*(grid_map_size.x-j)+grid_basis.y*(grid_map_size.y-i)-offset, grid_basis.x*(grid_map_size.x-j-1)+grid_basis.y*(grid_map_size.y-i-1)-offset, color)

	for i in range(1, grid_map_size.y, 3):
		if i <= grid_map_size.y/2:
			start = hex_map_size.x-1 - i/3
		else:
			start = (i-grid_map_size.y/2)/3

		for j in range(abs(parity-i%2), grid_map_size.x+1, 2):
			if j >= start and j <= grid_map_size.x-start:
				VisualServer.canvas_item_add_line(surf, grid_basis.x*j+grid_basis.y*i-offset, grid_basis.x*j+grid_basis.y*(i+2)-offset, color, width, antialiasing)

Пример:

Вертикальная ориентация

func _draw_vert_hex_grid(surf:RID, color:Color, width=1.0, antialiasing=false):
	var parity = int(hex_map_size.x)%2
	var offset = grid_basis.x*2+grid_basis.y + (1-parity)*grid_basis.y
	var start
	for j in range(0, grid_map_size.x/2, 3): # Drawing vertices
		start = hex_map_size.x - j/3 - 1
		for i in range(start, grid_map_size.y/2):
			if abs(i%2 - j%2) != parity:
				# Down diagonal
				VisualServer.canvas_item_add_line(surf, grid_basis.x*(j+1)+grid_basis.y*(i)-offset, grid_basis.x*(j)+grid_basis.y*(i+1)-offset, color)
				VisualServer.canvas_item_add_line(surf, grid_basis.x*(grid_map_size.x-j-1)+grid_basis.y*(i)-offset, grid_basis.x*(grid_map_size.x-j)+grid_basis.y*(i+1)-offset, color)

				VisualServer.canvas_item_add_line(surf, grid_basis.x*(j+1)+grid_basis.y*(grid_map_size.y-i)-offset, grid_basis.x*(j)+grid_basis.y*(grid_map_size.y-i-1)-offset, color)
				VisualServer.canvas_item_add_line(surf, grid_basis.x*(grid_map_size.x-j-1)+grid_basis.y*(grid_map_size.y-i)-offset, grid_basis.x*(grid_map_size.x-j)+grid_basis.y*(grid_map_size.y-i-1)-offset, color)
			else:
				# Top diagonal
				VisualServer.canvas_item_add_line(surf, grid_basis.x*(j)+grid_basis.y*(i)-offset, grid_basis.x*(j+1)+grid_basis.y*(i+1)-offset, color)
				VisualServer.canvas_item_add_line(surf, grid_basis.x*(grid_map_size.x-j)+grid_basis.y*(i)-offset, grid_basis.x*(grid_map_size.x-j-1)+grid_basis.y*(i+1)-offset, color)

				VisualServer.canvas_item_add_line(surf, grid_basis.x*(j)+grid_basis.y*(grid_map_size.y-i)-offset, grid_basis.x*(j+1)+grid_basis.y*(grid_map_size.y-i-1)-offset, color)
				VisualServer.canvas_item_add_line(surf, grid_basis.x*(grid_map_size.x-j)+grid_basis.y*(grid_map_size.y-i)-offset, grid_basis.x*(grid_map_size.x-j-1)+grid_basis.y*(grid_map_size.y-i-1)-offset, color)

	for i in range(1, grid_map_size.x, 3):
		if i <= grid_map_size.x/2:
			start = hex_map_size.x-1 - i/3
		else:
			start = (i-grid_map_size.x/2)/3

		for j in range(abs(parity-i%2), grid_map_size.y+1, 2):
			if j >= start and j <= grid_map_size.y-start:
				VisualServer.canvas_item_add_line(surf, grid_basis.x*i+grid_basis.y*j-offset, grid_basis.x*(i+2)+grid_basis.y*(j)-offset, color, width, antialiasing)

Пример:

Рисование шестиугольников

Тут на самом деле все просто, можете расслабиться. После этой жести с четностями ничего хуже уже не будет. Для рисования шестиугольников вспомним функции для получения вершин, которые я приводил выше и просто соеденим массив вершин шестиугольника линиями:

Функции для получения вершин, если лень мотать неаверх

func _get_vert_hex_vertices(hex):
	var pixel = hex2pixel(hex)
	return PoolVector2Array([
		pixel+2*grid_basis.x,
		pixel+grid_basis.x+grid_basis.y,
		pixel-grid_basis.x+grid_basis.y,
		pixel-2*grid_basis.x,
		pixel-grid_basis.x-grid_basis.y,
		pixel+grid_basis.x-grid_basis.y
	])
	
func _get_hor_hex_vertices(hex):
	var pixel = hex2pixel(hex)
	return PoolVector2Array([
		pixel+grid_basis.x-grid_basis.y,
		pixel+grid_basis.x+grid_basis.y,
		pixel+2*grid_basis.y,
		pixel-grid_basis.x+grid_basis.y,
		pixel-grid_basis.x-grid_basis.y,
		pixel-2*grid_basis.y,
	])

И рисуем множество линий между точками, не забыв замкнуть цепь:

func _draw_hor_hex(hex, surf, color, width=1.0, antialiasing=false):
	var points = _get_hor_hex_vertices(hex)
	points.append(points[0]) # замыкаем
	VisualServer.canvas_item_add_polyline(surf, points, [color], width, antialiasing)
	
func _draw_vert_hex(hex, surf, color, width=1.0, antialiasing=false):
	var points = _get_vert_hex_vertices(hex)
	points.append(points[0]) # замыкаем
	VisualServer.canvas_item_add_polyline(surf, points, [color], width, antialiasing)

Для заливки шестиугольника, по аналогии с прямоугольником, рисуем полигон:

func _fill_hor_hex(hex, surf, color, antialiasing=false):
	var points = _get_hor_hex_vertices(hex)
	VisualServer.canvas_item_add_polygon(surf, points, [color], [], RID(), RID(), antialiasing)
	
func _fill_vert_hex(hex, surf, color, antialiasing=false):
	var points = _get_vert_hex_vertices(hex)
	VisualServer.canvas_item_add_polygon(surf, points, [color], [], RID(), RID(), antialiasing)

Выглядит все это как то так:

Шестиугольные сетки в изометрии

Что может быть лучше сетки шестиугольников? Правильно, сетка шестиугольников в изометрии. Вы могли заметить, что ни в одной функции я не использовал числа — везде я работал с векторами. А это значит, что поменяв базис, автоматически поменяются функции — так и должно работать программирование. Помните, в части про преобразование координат я все вычисления автоматизировал? Так вот, наконец то нам это пригодится.

Как вы уже наверняка поняли, шестиугольная сетка это лишь обертка над обычной прямоугольной, ведь все функции рано или поздно сходятся к работе с базисами вспомогательной сетки. Поэтому для создания изометрии не будем придумывать велосипед, просто зададим ее переменной, отвечающей за искажение отношений горизонтальных размеров к вертикальным:

...
const iso_scale = 2.0

Тогда для изменения вида делим y-координату каждого базиса вспомогательной сетки на это искажение:

# Вертикальная ориентация
grid_basis.x = Vector2(long, 0)
grid_basis.y = Vector2(0, short/iso_scale)
			
# Горизонтальная ориентация	
grid_basis.x = Vector2(short, 0)
grid_basis.y = Vector2(0, long/iso_scale)

И все, даже не нужно менять базисы шестиугольной сетки, ведь мы их задавали через базисы вспомогательной. Вот пример:

На самом деле, благодаря векторным преобразованиям мы можем делать с базисами вспомогательной сетки все что угодно, и все функции все равно будут работать. Поэтому давайте сделаем сетку не просто в изометрии, а еще и повернем ее на 45°, также, как мы это делали в статье про прямоугольные сетки:

# для вертикальных
var pw = int(long*cos(PI/4))
var ph = int(short*cos(PI/4))

grid_basis.x = Vector2(pw, pw/iso_scale)
grid_basis.y = Vector2(-ph, ph/iso_scale)

# для горизонтальных
var pw = int(short*cos(PI/4))
var ph = int(long*cos(PI/4))

grid_basis.x = Vector2(pw, pw/iso_scale)
grid_basis.y = Vector2(-ph, ph/iso_scale)

Напомню, что базисы шестиугольной сетки мы не трогаем, ведь они все так же заданы через базисы вспомогательной. Выглядит вся эта магия как то так:

Красиво, конечно, но игру на этом не сделать. Нужно также уметь что-то на этих сетках делать.

Изометрические преобразования

С преобразованиями тоже мудрить ничего не стоит, ведь, напомню, шестиугольная сетка — это только обертка над обычной, поэтому все функции будут работать в штатном режиме. Единственное, что наверно стоит рассмотреть, это получение ячейки вспомогательной сетки, левый верхний угол которой находится в центре шестиугольника.

Для этого вспомним то, как мы направляли базисы для различных ориентаций шестиугольников. Вот картинка из почти самого начала моего рассказа:

Посмотрев на нее, все сразу становится ясно. В случае горизонтальной ориентации при каждом перемещении по x на шестигольной сетке мы двигаемся на две ячейки вспомогательной, а при движении по y мы движемся на одну ячейку вправо и на три вниз. Для вертикальных применима эта же логика. По этим формулам написать функции можно проще простого:

# Для вертикальных
func get_center_cell(hex:Vector2):
		return Vector2(hex.x*3, hex.y*2+hex.x)

# для горизонтальных
func get_center_cell(hex:Vector2):
		return Vector2(hex.x*2+hex.y, hex.y*3)

В изометрии ближние объекты должны рисоваться раньше дальних, и, если помните, в прямоугольных изометрических сетках мы использовали сумму координат. Здесь делаем тоже самое, только находим сумму координат центральной ячейки в шестиугольнике, получаемую по алгоритму выше.

Расстояние на сетке

Часто бывает нужно найти расстояние между двумя шестиугольниками. Для этого заметим, что при перемещении в любой из соседних шестиугольников меняются сразу две координаты из трех, причем на единицу. Тогда сумма модулей всех трех координат либо меняется на два, либо не изменятся вовсе. В таком случае сеточное расстояние от начала координат можно найти как половину суммы модулей трех координат шетиугольника, а для нахождения расстояния между двумя шестиугольниками можно просто найти смещение одного относительно другого через разность. Получается вот такая небольшая функция:

func hex_distance(hex1:Vector2, hex2:Vector2):
	var dif = (hex2-hex1)
	return (abs(dif.x) + abs(dif.y) + abs(-dif.x-dif.y))/2 # z = -x-y

Сеточное направление

Для поворота объекта в сторону ячейки на прямоугольных картах мы, если помните, находили направляющую ячейку. Здесь будем делать то же самое.

Это один из немногих алгоритмов, где нам понадобится третья координата. Для нахождения направляющей разделим сетку по трем осям и заметим, что в каждой части получившейся сетки одна из трех координат максимальна по модулю:

Теперь все, что нам нужно, это выбрать нужную часть и, сравнив модули не наибольших координат, выдать одно из осевых направлений, представленное в виде направляющей ячейки. Прямо на осях одна из координат всегда равна нулю, поэтому просто перехватим их как особые случаи. Для указания вдоль оси будем использовать знак разности конечного и начального шестиугольников. Также заметим, что на диагональных ячейках модули не наибольших координат равны, поэтому мы можем смещаться в любую из двух осей. Я выбрал смещение в сторону оси по часовой стрелке, в коде это выражается строгостью знака сравнения. Для смещения против часовой стоит допустить равенство. Так выглядит этот алгоритм в коде:

func direct_hex(hex1:Vector2, hex2:Vector2):
	var dx = hex2.x - hex1.x
	var dy = hex2.y - hex1.y
	var dz = -hex2.x-hex2.y + hex1.x+hex1.y
	if dx == 0: # Ось y
		return Vector2(0, sign(dy)) # Возвращаем ось y
	elif dy == 0: # Ось x
		return Vector2(sign(dx), 0) # Возвращаем ось x
	elif dz == 0: # Ось z
		return Vector2(sign(dx), sign(dy)) # Возвращаем ось z
	else:
		if abs(dz) > abs(dx) and abs(dz) > abs(dy): # модуль разности по z оказался наибольшим
			if abs(dx) > abs(dy): # т.к. разность по x больше, значит мы отошли по x дальше, чем по y, значит выдаем ось x
				return Vector2(sign(dx), 0) # возвращаем ось x
			else: # т.к. разность по y больше, значит мы отошли по y дальше, чем по x, значит выдаем ось y
				return Vector2(0, sign(dy)) # возвращаем ось y
        
		elif abs(dy) > abs(dx): # модуль разности по y оказался наибольшим
			if abs(dz) > abs(dx): # по аналогии
				return Vector2(0, sign(dy)) # возвращаем y. Это связанно с представлением z-координаты через две другие
			else: # по аналогии
				return Vector2(sign(dx), sign(dy)) # возвращаем z
        
		else: # модуль разности по x оказался наибольшим
			if abs(dy) > abs(dz): # по аналогии
				return Vector2(sign(dx), sign(dy)) # возвращаем z
			else: # по аналогии
				return Vector2(sign(dx), 0) # возвращаем x

Принцип работы этого алгоритма тот же, что и в статье про прямоугольгные сетки. Мы смотрим на разницы координат и по ним определяем направляющую. Как мы видим, все рабоатет:

На всякий случай скажу, что этот алгоритм не зависит от ориентации шестиугольников, ведь работа идет с их координатами, а координатам внутри сетки вообще плевать на положение шестиугольников в пространстве.

Поиск пути

Основной алгоритм поиска пути тот же, что и у обычной прямоугольной сетки, отличаются только соседи и проверки на нахождение точки внутри карты. Главный алгоритм — A*, его не трогаем совсем.

Соседи у шестиугольника выглядят как то так:

Можно заметить, что они также не зависят от ориентации шестиугольников, поэтому в будущем будем пользоваться одной функцией для обоих случаев.

Также у разных видов карты отличаются проверки на принадлежность шестиугольниа им. Алгоритмы для разных ориентаций шестиугольников немного отличаются, но в целом они похожи, поэтому пояснять я буду только на примере горизонтальных, а для вертикальных оставлю уже готовые функции.

Начнем с прямоугольной карты. Для наглядности напомню как она выглядит:

Синим обозначены границы карты. Оси в такой сетке идут не параллельно сторонам прямоугольника, поэтому просто ограничить их нулем и границей карты не выйдет. Так сработает только для Y оси сетки, а горизонтальные границы зависят от смещения по Y. Перемещаясь вдоль оси Y, расстояние до левой границы в ячейках вспомогательной сетки увеличивается на единицу, значит на половину шестиугольника. Аналогично с правой границей, тоолько до нее расттояние уменьшается. При округлении левой границы используем floor, т.к. когда граница проходит ровно между шестиугольниками, мы выбираем тот, что внутри. По аналогии используем ceil для правой границы:

func _in_rect_grid_hor(hex):
	return hex.x >= -floor(hex.y/2) and hex.x < hex_map_size.x-ceil(hex.y/2) and hex.y < hex_map_size.y and hex.y >= 0

Для вертикальной ориентации логика точно такая же. Вот функция для нее:

func _in_rect_grid_vert(hex):
	return hex.x >= 0 and hex.x < hex_map_size.x and hex.y >= -floor(hex.x/2) and hex.y < hex_map_size.y-ceil(hex.x/2)

Теперь про шестиугольную карту. Ее вид:

Для простоты вычислений будем считать границы от центра карты. Просто потыкав и посмотрев на координаты я пришел к следующим формулам центров:

# для горизонтальных
func _get_hor_hex_map_center():
	return Vector2(int((hex_map_size.x-1)/2), hex_map_size.x-1)

# для вертикальных
func _get_vert_hex_map_center():
	return Vector2(hex_map_size.x-1, int((hex_map_size.x-1)/2))

Каждому смещению по Y соответствует уменьшение длины ряда на единицу, так и будем задавать границы по x. В качестве размеров, ограничивающих карту, возьмем диагональ. Как ее вычислять я рассказывал ранее. Тогда по Y границами будут просто половины этих диагоналей, а по X одна из граней всегда параллельна оси Y, поэтому уменьшаться будет либо правая либо левая граница. Какая именно можно понять по вертикальной половине шестиугольника. Если мы находимся в верхней, то уменьшается левая граница (т.к. правая параллельна оси Y), если в нижней то уменьшается правая граница (т.к. левая паралельна оси Y). А если мы находимся прямо на горизонтальной диагонали то нам плевать, ведь на ней смещение по Y равно нулю.

Вот функции, реализующие данную логику для обеих ориентаций:

# для горизонтальных
func _in_hex_grid_hor(hex):
    var center = _get_hor_hex_map_center()
    var diag = int(hex_map_size.x*2 - 1)
    hex -= center # Vector2 passed by value; getting hex regarding map center
    if hex.y < 0:
        return hex.x >= -diag/2+abs(hex.y) and hex.x <= diag/2 and hex.y >= -diag/2 and hex.y <= diag/2
    else:
        return hex.x >= -diag/2 and hex.x <= diag/2-abs(hex.y) and hex.y >= -diag/2 and hex.y <= diag/2

# для вертикальных
func _in_hex_grid_vert(hex):
    var center = _get_vert_hex_map_center()
    var diag = int(hex_map_size.x*2 - 1)
    hex -= center # Vector2 passed by value; getting hex regarding map center
    if hex.x < 0:
        return hex.y >= -diag/2+abs(hex.x) and hex.y <= diag/2 and hex.x >= -diag/2 and hex.x <= diag/2
    else:
        return hex.y >= -diag/2 and hex.y <= diag/2-abs(hex.x) and hex.x >= -diag/2 and hex.x <= diag/2

Для проверки поставим условие, что для рисования шестиугольника под курсором он должен быть внутри сетки:

Отлично, теперь можно спокойно реализовывать алгоритм поиска пути:

Ищем путь истинный

class PriorityStack:
	
	var items:Array
	
	func _init():
		items = Array()
		
	func empty() -> bool:
		return items.size() == 0
		
	func put(item, priority:int) -> void:
		if empty():
			items.append([item, priority])
		elif priority <= items[0][1]:
			items.insert(0, [item, priority])
		elif priority > items[-1][1]:
			items.append([item, priority])
		else:
			for i in range(len(items)):
				if priority <= items[i][1]:
					items.insert(i, [item, priority])
					break
					
	func take():
		return items.pop_front()[0]

func in_map(hex):
	match grid_type:
		GridTypes.hex:
			if hex_type == HexTypes.hor:
				return _in_hex_grid_hor(hex)
			else: # Vertical
				return _in_hex_grid_vert(hex)
		GridTypes.rect:
			if hex_type == HexTypes.vert:
				return _in_rect_grid_vert(hex)
			else: # Hor orientation
				return _in_rect_grid_hor(hex)

func can_stand(hex:Vector2, obsts:PoolVector2Array):
	return in_map(hex) and not (hex in obsts)
	
func neighbors(hex_pos:Vector2, obsts:PoolVector2Array):
	var res:PoolVector2Array = []
	var _neighbors = PoolVector2Array([Vector2(-1, 0), Vector2(1, -1), Vector2(0, -1), Vector2(1, 0), Vector2(0, 1), Vector2(-1, 1)])
	for i in _neighbors:
		if can_stand(i+hex_pos, obsts):
			res.append(i+hex_pos)
	return res
	
func find_path(start:Vector2, goal:Vector2, obsts:PoolVector2Array):
	var frontier = PriorityStack.new()
	frontier.put(start, 0)
	var came_from = {}
	var cost_so_far = {}
	came_from[start] = start
	cost_so_far[start] = 0
	
	var current:Vector2
	var new_cost:int
	
	if not can_stand(goal, obsts):
		return PoolVector2Array()
		
	while not frontier.empty():
		current = frontier.take()
		
		if current == goal:
			break
			
		for next in neighbors(current, obsts):
			new_cost = cost_so_far[current] + 1
				
			if not (next in cost_so_far) or new_cost < cost_so_far[next]:
				cost_so_far[next] = new_cost
				frontier.put(next, new_cost+hex_distance(goal, next))
				came_from[next] = current
				
	if frontier.empty() and current != goal:
		return PoolVector2Array()
		
	current = goal
	var path = PoolVector2Array([current])
	
	while current != start:
		current = came_from[current]
		path.append(current)
	
	path.invert()
	path.remove(0) # removes first position
	return path

func hex_distance(hex1:Vector2, hex2:Vector2):
	var dif = (hex2-hex1)
	return (abs(dif.x) + abs(dif.y) + abs(-dif.x-dif.y))/2

Данный код я взял напрямую из своей реализации, так что некоторые моменты не освещены, за ненадобностью. Поглазеть на полный код сможете кликнув по ссылке в конце статьи. Так это выглядит:

Растеризация отрезка

Вот с растеризацией у шестиугольной сетки большие проблемы. Можно, конечно, придумать что нибудь с алгоритмом брезенхема для растеризации отрезков, однако я не думаю что вам нужно растеризовывать по 1000 отрезков за кадр, поэтому на оптимизацию позволим себе немного подзабить и воспользуемся линейной интерполяцией, которую, кстати, и предлагает автор популярной англоязычной статьи. Думаю почти все знают что такое линейная интерполяция, поэтому просто оставлю тут реализацию алгоритма:

Растеризуем нерастеризуемое

func rast_line(hex1, hex2):
	var N = hex_distance(hex1, hex2)
	if N == 0: return PoolVector2Array([hex1])
	var res = PoolVector2Array()
	for i in range(N+1):
		res.append(round_hex(lerp(hex1, hex2, i/N)))
	return res

Вот так это выглядит:

Пару слов в завершение

Вот и подошел столь запутанный рассказ к концу. Я постарался объяснить все максимально подробно и вставлял как можно больше картинок, надеюсь не зря. Никакую маленькую игру я делать не стал, ибо тут и так хаватает над чем подумать, поэтому просто оставлю код получившегося класса на почти 500 строк. Я подразумеваю его использование через автозагрузку, как собственно я и делал во время работы над ним.

Если я забыл про что-то рассказать или упустил какие-то важные моменты, или же просто ошибаюсь, напишете об этом в комментарии.

Я надеюсь эта статья позволит вам полностью реализовать давние мечты по созданию «убийцы героев» или что она позволила просто интересно провести вечер. До скорого!

Прямоугольные тайловые миры / Хабр

Тайлы — пожалуй один из самых удобных способов построения игровой логики. Все происходит максимально дискретно, никаких тебе физик с просчетом коллизий и прочими трудностями.

Огромное множество игр на самом деле содержат тайлы — так просто проще представлять игровой мир. Такая упорядоченность помогает геймдизайнерам строить игровые механики, упрощает жизнь художников и делает код программистов понятнее. Самих видов тайлов тоже огромное количество — сегодня поговорим о прямоугольных и изометрических.

Не стоит воспринимать все сказанное здесь как научную истину, многие вещи выведены мной, так что не стесняйтесь исправлять, ругать и дополнять меня в комментариях. Все примеры сделаны на движке Godot Engine v. 3.2.3 с использованием его встроенного языка.

Думаю в целом язык понятен, но вот ссылки на некоторые функции из документации:

Данный метод рисования может быть вам не знаком, но я писал о нем ранее тут.

Прямоугольные сетки

Начнем с чего попроще — прямоугольных сеток. Такой тип представления игровой логики наверное максимально распространен в настольных играх, как пример — шахматы. В них фигуры ходят и бьют строго по клеткам на ограниченной размером 8×8 ячеек доске (ну мало ли кто то не знает). Не удивительно что из-за такой простоты и вариативности эта дисциплина быстро распространилась на компьютеры. Давайте же смотреть как это все устроено.

Система координат

Для понимания игрового мира необходима система координат. Обычно она состоит из двух осей (для двумерного мира) — X и Y. Внутри самой сетки направим оси как экранные — ось X вправо, ось Y вниз. Единичные отрезки представляют ячейки. Для связи сеточной системы отсчета с экранной необходимы базисные векторы, которые будут направлены вдоль осей сетки. Длины таких векторов будут равны размерам ячейки в пикселях, а начало системы отсчета, аналогично экранной, поместим в левый верхний угол:

В коде задаем ширину и высоту ячейки, и уже через эти размеры определяем базисы:

const cell_width = 48 # width of cell in pixels
const cell_height = 32 # height of cell in pixels
# Basis vectors
var srv = Vector2(cell_width, 0) # screen-right-vector
var sdv = Vector2(0, cell_height) # screen-down-vector

Преобразование координат

С преобразованием ячейки в пиксель проблем возникнуть не должно. Если клетка имеет координаты {x; y}, это значит, что на экране она находится на x горизонтальных и на y вертикальных базисов от начала координат:

func cell2pixel(cell:Vector2) -> Vector2:
	return srv*cell.x + sdv*cell.y

После такого преобразования получаем левый верхний угол ячейки. Для нахождения ее центра просто прибавляем по половинке базисных векторов:

func cell2pixel_center(cell:Vector2) -> Vector2: # To cell center
	return cell2pixel(cell)+srv/2+sdv/2 # cell2pixel returns left-top corner

В расчетах это понадобится вряд ли, а вот для рисования в самый раз. Например, для соединения двух ячеек линией гораздо больше подойдет соединение центров, ведь так просто понятнее и эстетичнее:

А как из пикселя получить ячейку? Если говорить простым языком, точка лежит в ячейке, пока она находится в пределах ее длины и высоты. Это означает, что для смещения к следующей ячейке необходимо переместится на ее размер на экране. Тогда точные координаты в сеточной системе отсчета можно найти через деление каждой координаты пикселя на соответствующий ей размер ячейки. В результате деления получится дробное число, вещественная часть которого показывает смещение пикселя внутри клетки относительно ее верхнего угла. Т.к. нас интересует только ячейка, округлим к ближайшему меньшему целому. Это важно, ведь при маленьких дробных отрицательных значениях (по модулю <1) приведение к int все равно покажет 0, хотя это уже отрицательная часть:

func pixel2cell(pixel:Vector2) -> Vector2:
	var x = floor(pixel.x/cell_width)
	var y = floor(pixel.y/cell_height)
	return Vector2(x, y)

Однако такие преобразования можно описать более точно, с помощью математики. Мы имеем базис из векторов srv{cell_width; 0} и sdv{0; cell_height}. Представив его в виде матрицы запишем преобразование координат ячейки в координаты пикселя как произведение матрицы и вектора:

А для нахождения отсюда pixel нужно обратить матрицу:

Раскрыв выражения получим то же самое, что и ранее. Я согласен с тем что этот подход тут неуместен, однако далее вы увидите всю его настоящую мощь.

Как видим, все прекрасно работает:

К сожалению, сетка и этот прекрасный желтый прямоугольник появляются не по щучьему велению, поэтому рисуем это тоже сами.

Рисование сетки

Алгоритм рисования не отличается от разлиновывания чистого листа — просто рисуем вертикальные и горизонтальные линии с одинаковым интервалом. Для рисования сетки необходимо знать ее размеры:

const map_width = 5
const map_height = 5

Тогда в качестве интервала между разделителями берем размеры ячейки, а в циклах идем от нуля до края карты. Т.к. нам нужна закрытая со всех сторон сетка, необходимо рисовать на одну линию больше, иначе какие-то две стороны останутся открытыми:

func draw_grid(surf:RID, color:Color, width=1.0, antialiasing=false) -> void:
	for i in range(map_width+1):
		VisualServer.canvas_item_add_line(surf, cell2pixel(Vector2(i, 0)), cell2pixel(Vector2(i, map_height)), color, width, antialiasing)
	for i in range(map_height+1):
		VisualServer.canvas_item_add_line(surf, cell2pixel(Vector2(0, i)), cell2pixel(Vector2(map_width, i)), color, width, antialiasing)

Получаем обычную прямоугольную сетку, то что нужно:

Если необходима открытая сетка, то начинаем с единицы, чтобы не было верхней и левой границ, и при этом рисуем линии до крайних ячеек, не закрывая их справа и снизу:

func draw_open_grid(surf:RID, color:Color, width=1.0, antialiasing=false) -> void:
	for i in range(1, map_width):
		VisualServer.canvas_item_add_line(surf, cell2pixel(Vector2(i, 0)), cell2pixel(Vector2(i, map_height)), color, width, antialiasing)
	for i in range(1, map_height):
		VisualServer.canvas_item_add_line(surf, cell2pixel(Vector2(0, i)), cell2pixel(Vector2(map_width, i)), color, width, antialiasing)

Рисование ячейки

В играх необходимо показать пользователю ячейку, на которую указывает курсор. Для этого чаще всего ее просто выделяют, обводят цветом. В случае прямоугольных тайлов нам необходимо нарисовать четыре линии, то бишь каждую сторону ячейки. В Godot есть удобная функция для рисования отрезков между точками, надо только не забыть замкнуть цепочку — именно поэтому левый верхний угол встречается дважды:

func draw_cell(cell:Vector2, surf:RID, color:Color, width=1.0, antialiasing=false):
	var points = PoolVector2Array([
		cell2pixel(cell), # Левый верхний угол
		cell2pixel(cell)+srv, # Прибавили правый базис, правый верхний угол
		cell2pixel(cell)+srv+sdv, # Прибавили оба базиса, правый нижний угол
		cell2pixel(cell)+sdv, # Прибавили нижний базис, левый нижний угол
		cell2pixel(cell) # Замыкаем цепочку
	])
	VisualServer.canvas_item_add_polyline(surf, points, [color], width, antialiasing) 

А для заливки ячейки рисуем залитый прямоугольник по координатам левого верхнего угла и с размерами ячейки:

func fill_cell(cell:Vector2, surf:RID, color:Color) -> void:
	VisualServer.canvas_item_add_rect(surf, Rect2(cell2pixel(cell), Vector2(cw, ch)), color)

Выглядит это как то так:

Изометрические сетки

Если вы промотали часть про прямоугольные сетки досюда — я не удивлен. Во всяком случае они выглядят не так красиво, как изометрические. Вообще такой стиль в свое время опередил технологии — он создал объем тогда, когда это еще не было доступно в виду ограниченности технологических ресурсов. Типичным представителем являются в свое время очень популярные казаки:

Казаки

А сейчас же изометрия используется в основном только инди студиями, да и спрайты выглядят гораздо проще — обычно это несложный пиксель-арт. Одним из ярчайших примеров является Into the Breach, обладатель нескольких наград и покоритель моего сердца своим шахмато-подобным геймплеем.

Into the Breach

Система координат

Часто в играх изометрию представляют как повернутую на 45° и сжатую по вертикали вдвое обычную сетку, поэтому система координат внутри сетки останется прежней, а базисные векторы все также направлены вдоль сеточных осей:

Для задания размера ячейки использовать ее сторону не очень удобно, ведь при вертикальных искажениях ее размер меняется. Гораздо практичнее взять какую то постоянную величину, тогда через нее можно задавать любые другие. В качестве такой отлично подойдет горизонтальная диагональ ячейки, ведь при любых изменениях она сохраняет свой размер:

Координаты базисных векторов можно найти как проекции на экранные оси. Тогда при проецировании проекции будут ровно попадать в диагонали, ведь они параллельны экранным осям. Для синего (X) базиса это будут половина горизонтальной диагонали по X и половина вертикальной по Y. Для красного (Y) все тоже самое, только его проекция на экранную ось X будет отрицательной.

Зададим размер ячейки и два значения — cw как половина горизонтальной диагонали и ch как половина вертикальной. Как упоминалось ранее, сетка сжимается по вертикали вдвое, значит вертикальная диагональ, изначально равная горизонтальной, тоже уменьшилась вдвое:

const cell_size = 60
# работать с int гораздо проще, поэтому убираем вещ. часть,
# от этого сильно ничего не поменяется.
cw = int(cell_size/2) # cell-width
ch = int(cw/2) # cell-height

Через эти значения базисные векторы можно задать проще простого:

...
right_basis = Vector2(cw, ch) # вектор по X
left_basis = Vector2(-cw, ch) # вектор по Y

Преобразование координат

С преобразованием ячейки в пиксель все точно так же, просто умножаем каждую координату на соответствующий ей базис:

func cell2pixel(cell:Vector2) -> Vector2:
	return cell.x*right_basis + cell.y*left_basis

Для получения центра ячейки аналогично прямоугольной сетке прибавляем по половинке базисов:

func cell2pixel_center(cell:Vector2) -> Vector2:
	return cell2pixel(cell)+right_basis/2+left_basis/2

А вот с преобразованием пикселя в ячейку все немного посложнее, просто логикой не обойдешься. Запишем перевод из сеточной системы отсчета в экранную:

Тогда для получения отсюда ячейки cell обращаем матрицу и раскрываем выражение:

После этого опять же получаются дробные значения, вещественная часть которых показывает смещение пикселя в ячейке, которое нас, напомню, не интересует, поэтому округляем значение к меньшему целому, по той же причине, что и у прямоугольной сетки. Также заметим, что 2^-1 можно вынести и разделить уже полученный результат, аккурат перед округлением:

func pixel2cell(pixel:Vector2) -> Vector2:
	var x = pixel.x/cw + pixel.y/ch
	var y = pixel.y/ch - pixel.x/cw
	return Vector2(floor(x/2), floor(y/2))

Кто ничего не понял, просто пользуется готовой формулой. Она работает, честно. А вот как это выглядит:

Преобразование угла

Как найти угол между двумя ячейками понятно — находим соединяющий их вектор через разность, потом определяем его угол. Но могут возникнуть проблемы когда нам известен только угол. Например, корабль хочет выстрелить вправо, т.е. под 0° относительно себя. Такое направление указывает вдоль горизонтальной оси, но мы знаем, что изометрическая ось не особенно то и совпадает с экранной. Как перевести одно в другое мы уже выяснили, а если угол произвольный? Тут тоже пригодятся описанные выше преобразования. Представим угол через вектор с координатами {cos a; sin a} и прогоним его через ту же функцию, после чего найдем угол вектора с преобразованными координатами:

func iso2linear(angle:float) -> float:
	var x = cos(angle)
	var y = sin(angle)
	return cell2pixel(Vector2(x, y)).angle()

Точно также преобразуется экранный угол в изометрический, только тут используются формулы напрямую, т.к. готовая функция округляет результат, а при работе с такими маленькими величинами целая часть всегда будет равна нулю. Также я опустил деление на 2, ведь от него направление все равно не меняется:

func linear2iso(angle:float) -> float:
	var x = cos(angle)
	var y = sin(angle)
	var x1 = x/cw + y/ch
	var y1 = y/ch - x/cw
	return Vector2(x1, y1).angle()

Тут красный вектор показывает изометрический угол между двумя ячейками, зеленый — преобразованный экранный угол:

Как мы видим, приближаясь к основанию ячейки (верхнему углу), зеленый вектор стремится к красному, значит все работает правильно.

Произвольное изометрическое искажение

Соотношение сторон 1:2 было выбрано не случайно, так просто удобнее художникам рисовать спрайты и компьютерам линии, ведь при рисовании отрезков одному шагу наверх соответствуют два шага вправо, тут не надо никаких алгоритмов Брезенхема. Однако вычислительные мощи подросли, поэтому мы можем позволить себе любые капризы. На самом деле все делается не сложнее того, что делалось ранее: достаточно поменять пару значений. Пусть за это соотношение отвечает некоторая переменная:

var iso_scale = 2.0

Тогда единственное, что нужно поменять, это значение переменной ch:

...
ch = int(cw/iso_scale)
...

И все. Все предыдущие функции будут работать как прежде. Вот, например, соотношение 1 к 1.43:

Порядок рисования объектов

Вряд ли вы хотите увидеть в своей игре что такое:

Те блоки, которые ближе к нам, перекрываются дальними, поэтому создается впечатление что мы строим в высоту, хотя это не так. Если в простой прямоугольной сетке мы можем определять порядок отрисовки по Y координате, то здесь оба базиса смотрят вниз и определить по одному из них порядок рисования не выйдет. В изометрии мы можем сортировать объекты по диагоналям, потому как их ряды идут точно вниз. Каждая ячейка в ряду имеет одну и ту же сумму координат, поэтому именно эту сумму мы и будем использовать как z_index объекта (в godot эта переменная у двумерных объектов обозначает порядок их рендера. Чем этот индекс выше, тем позже рисуется объект):

При изменении позиции приравниваем z_index к pos.x+pos.y (pos — позиция объекта на сетке):

func set_pos(cell):
	pos = cell # сохраняем значение в свою локальную переменную
	position = Grid.cell2pixel(pos) # ставим объект на экране в нужную точку
	z_index = pos.x+pos.y # устанавливаем порядок отрисовки

Теперь все рисуется как надо и создается необходимая иллюзия объема:

Прямоугольные изометрические сетки

Квадратные сетки конечно здорово, но с ними как то не особо разбежишься. Вдруг мне захочется сделать игру про кораблики, которые вытянуты вдоль? Тогда использовать квадратные тайлы нерентабельно, остается много пустого места. Для такой игры как раз подойдут прямоугольные сетки.

Система координат

Система координат внутри сетки все остается прежней, потому как, напоминаю, мы меняем только вид на нее. Базисы точно также будут направлены вдоль изометрических осей, а вот для задания их координат необходимо повозиться. Дело в том, что у таких ячеек нет размеров, независящих от вертикальных преобразований, все стороны и диагонали будут менять свои размеры. Но мы же знаем, что при вертикальных преобразованиях точки не перемещаются по X, а это значит что проекции всех величин на эту ось тоже сохраняются. В качестве размеров можно взять просто длину и высоту, как в случае с обычными прямоугольными сетками. Это будут размеры в натуральную величину, т.е. при отсутствии изометрических искажений, и именно при таком виде можно и найти проекции. Без искажений угол между экранной горизонтальной осью и обеими изометрическими будет 45°. Используя его, найдем проекции:

const cell_width = 93 # Real cell width
const cell_height = 67 # Real cell height

pw = int(round(cell_width*cos(PI/4))) # Проекция длины
ph = int(round(cell_height*cos(PI/4))) #  Проекция высоты

Тогда синий вектор будет иметь координаты {pw; pw}, а красный {-ph; ph}. Для создания изометрического искажения просто делим Y-компоненту каждого базиса на коэффициент этого искажения:

const iso_scale:float = 2.0
...
srd = Vector2(pw, pw/iso_scale) # screen-right-down
sld = Vector2(-ph, ph/iso_scale) # screen-left-down

Преобразование координат

С преобразованием ячейки в пиксель все точно также, просто умножаем координаты на базисы:

func cell2pixel(cell):
	return cell.x*srd+cell.y*sld

И с получением центра ничего не поменялось (да ладно):

func cell2pixel_center(cell): # To cell center
	return cell2pixel(cell)+srd/2+sld/2

Да и для преобразования пикселя в ячейку проворачиваем тот же трюк:

Повторение мать учения

Выносим двойку и округляем:

func pixel2cell(pixel):
	var x = pixel.x/pw + iso_scale*pixel.y/pw
	var y = iso_scale*pixel.y/ph-pixel.x/ph
	return Vector2(floor(x/2), floor(y/2))

Ну и куда же без визуализации:

Рисование сетки

С рисованием тоже особо ничего не поменялось, просто рисуем линии в цикле от начала до края карты:

func draw_grid(surf, color, width=1.0, antialiasing=false):
	for i in range(map_width+1):
		VisualServer.canvas_item_add_line(surf, cell2pixel(Vector2(i, 0)), cell2pixel(Vector2(i, map_height)), color, width, antialiasing)
	for i in range(map_height+1):
		VisualServer.canvas_item_add_line(surf, cell2pixel(Vector2(0, i)), cell2pixel(Vector2(map_width, i)), color, width, antialiasing)

И рисование ячейки не тоже изменилось:

func draw_cell(cell, surf, color, width=1.0, antialiasing=false):
	var points = PoolVector2Array([
		cell2pixel(cell),
		cell2pixel(cell)+srd,
		cell2pixel(cell)+srd+sld,
		cell2pixel(cell)+sld,
		cell2pixel(cell),
	])
	VisualServer.canvas_item_add_polyline(surf, points, [color], width, antialiasing)

Для заливки ячейки нарисуем полигон, ограниченный четырьмя вершинами тайла:

func fill_cell(cell, surf, color):
	var points = PoolVector2Array([
		cell2pixel(cell),
		cell2pixel(cell)+srd,
		cell2pixel(cell)+srd+sld,
		cell2pixel(cell)+sld
	])
	VisualServer.canvas_item_add_polygon(surf, points, [color])

Алгоритмы на сетках

Рисовать сетки конечно здорово, но на этом далеко не уедешь. В игре должны быть какие то механики, какое то движение и интерактивность, без этого это просто приложение, рисующее красивые (или не очень) картинки.

Поворот изометрического объекта

В играх часто нужно направить объект на курсор. В случае top-down вида это делается поворотом самого спрайта объекта, а вот в псевдо 3d вращать спрайт не очень хорошая затея:

Для создания объема необходимо несколько спрайтов, по одному на каждое направление. Для выбора нужного спрайта необходимо понять, какое из 8-ми направлений наиболее близко к направлению до курсора. Каждое из них можно задать как относительную ячейку, ({-1; 0} — влево, {-1, -1} — влево вверх и т.д.) и искать направление до клетки через направляющие. Звучит немного непонятно, поэтому поясню. Чтобы перейти из ячейки {1, 2} в ячейку {5, 2} нам необходимо передвинутся вправо 4 раза. Понять мы это можем вычитанием из конечной ячейки начальной (5-1 = 4). Сколько именно раз надо передвинутся нам не важно, нас интересует направление. В данном случае разница между координатами положительна, значит двигаемся вдоль оси X. Тоже самое и с вертикальными координатами. Однако если мы просто запишем знаки разностей в координаты направляющего вектора, получится неравномерное распределение, ведь достаточно разности в единицу, чтобы указывать на это направление. Тут лучше показать:

Как мы видим, кораблик смотрит вдоль осей только тогда, когда мы указываем прямо на них, а в остальных случаях он смотрит в какой то из углов. Так дело не пойдет, надо как то расширять осевые направления. Тут нам поможет разность модулей разностей координат (WAT). Например, прямо на угловом направлении разность разностей равна нулю, ведь мы сдвинулись на однинаковое количество тайлов по вертикали и горизонтали. Получается, чем разность разностей больше, тем мы дальше отошли от углов. Для создания ограничения мы можем поставить условие, что если разность разностей больше какого либо числа, то это уже осевое наравление. Какое именно можно узнать, сравнив модули разностей координат. Если разность больше по X, значит это горизонтальное направление, иначе вертикальное. В качестве значения этой константы я выбрал 4, мне она показалась наиболее правдоподобной:

func direct_cell(cell1, cell2):
	var res = cell2-cell1 # вектор разности
	if abs(abs(res.x)-abs(res.y)) > 4: # Проверяем, осевое ли это направление
		if abs(res.x) > abs(res.y): # Если да, то смотрим какое именно
			return Vector2(sign(res.x), 0) # Разница по x больше, значит горизонтальное
		else:
			return Vector2(0, sign(res.y)) # Разница по y боьше, значит вертикальное
	else:
		return Vector2(sign(res.x), sign(res.y)) # Угловове направление

Для удобной работы со спрайтами их можно разместить кругом:

И брать спрайт по тем же координатам относительно центра, какие имеет направляющая ячейка. В центре находится тот спрайт, который мы хотим показывать когда игрок указывает прямо на ячейку кораблика. В результате все работает как надо:

Поиск пути

Пожалуй это все еще самый животрепещущий вопрос, хотя на эту тему написано огромное количество статей разнообразной сложности. Долго тут я распинаться не буду, потому что за меня уже все сказали. Для погружения в эту тему порекомендую данную статью на английском со всякими интерактивными демками или ее перевод на Хабре с простыми картинками. От себя я лишь оставлю реализацию A* на godot:

Реализация

class PriorityStack:
	
	var items:Array
	
	func _init():
		items = Array()
		
	func empty() -> bool:
		return items.size() == 0
		
	func put(item, priority:int) -> void:
		if empty():
			items.append([item, priority])
		elif priority <= items[0][1]:
			items.insert(0, [item, priority])
		elif priority > items[-1][1]:
			items.append([item, priority])
		else:
			for i in range(len(items)):
				if priority <= items[i][1]:
					items.insert(i, [item, priority])
					break
					
	func take(): # "get" name already taken by Variant
		return items.pop_front()[0]

func in_map(grid_pos:Vector2, map_size:Vector2) -> bool:
	return grid_pos.x < map_size.x and grid_pos.x >= 0 and grid_pos.y >= 0 and grid_pos.y < map_size.y

func can_stand(grid_pos:Vector2, obsts:PoolVector2Array, map_size:Vector2) -> bool:
	return not (grid_pos in obsts) and in_map(grid_pos, map_size)

func neighbors(grid_pos:Vector2,  obsts:PoolVector2Array, map_size:Vector2) -> PoolVector2Array:
	var res:PoolVector2Array = []
	var _neighbors = PoolVector2Array([grid_pos+Vector2(-1, 0), grid_pos+Vector2(1, 0), 
		grid_pos+Vector2(0, -1), grid_pos+Vector2(0, 1)])
	for neigh in _neighbors:
		if can_stand(neigh, obsts, map_size):
			res.append(neigh)
	return res

func heuristic(a:Vector2, b:Vector2) -> int:
	return int(abs(a.x-b.x)+abs(a.y-b.y))

func find_path(start:Vector2, goal:Vector2, obsts:PoolVector2Array, map_size:Vector2) -> PoolVector2Array:
	var frontier = PriorityStack.new()
	frontier.put(start, 0)
	var came_from = {}
	var cost_so_far = {}
	came_from[start] = start
	cost_so_far[start] = 0
	
	var current:Vector2
	var new_cost:int
	
	if not can_stand(goal, obsts, map_size):
		return PoolVector2Array()
		
	while not frontier.empty():
		current = frontier.take()
			
		if current == goal:
			break
			
		for next in neighbors(current, obsts, map_size):
			new_cost = cost_so_far[current] + 1
				
			if not (next in cost_so_far) or new_cost < cost_so_far[next]:
				cost_so_far[next] = new_cost
				frontier.put(next, new_cost + heuristic(goal, next))
				came_from[next] = current
				
	if frontier.empty() and current != goal:
		return PoolVector2Array()
		
	current = goal
	var path:PoolVector2Array = PoolVector2Array([current])
	
	while current != start:
		current = came_from[current]
		path.append(current)
	
	path.invert()
	path.remove(0) # removes first position
	return path

Это версия алгоритма без различных модификаций для получения более красивых путей или для каких то определенных карт. Данный код не претендует на минимальный расход памяти и максимальную скорость, но он работает и работает надежно, я переношу его с платформы на платформу уже года 2 🙂 А вот доказательство:

Растеризация различных фигур

Также важными задачами являются растеризации фигур для их отображения на экране. К счастью, многие из них уже решены. На сайте национального открытого университета ИНТУИТ есть целый раздел, посвящённый растровой графике. Там в том числе есть и алгоритмы растеризации различных штук. В целом, рекомендую глянуть, хоть все и рассказано достаточно сложным для понимания языком. Стоит сказать что я не очень то силен в данной теме, поэтому здесь возможны грубые ошибки. Если таковые найдете, попрошу указать на них в комментариях.

Для растеризации отрезка еще в 1962 был предложен алгоритм Брезенхема. До сих пор он остается одним из самых быстрых и оброс огромным количеством модификаций, еще сильнее ускоряющих его работу. Пояснять смысл его работы я тоже не вижу смысла, это слишком обширная тема для данного поста. На Хабре есть хоть и небольшая, но информативная статья на эту тему. Я только оставлю реализацию на godot с примером работы:

Алгоритм брезенхема

Тут реализована максимально простая версия алгоритма, опять же не претендующая на максимум производительности:

func rast_line(start:Vector2, goal:Vector2) -> PoolVector2Array:
	var res:PoolVector2Array = []
	var steep = abs(goal.y-start.y) > abs(goal.x-start.x)
	if steep:
		start = Vector2(start.y, start.x)
		goal = Vector2(goal.y, goal.x)
	var reverse = start.x > goal.x
	if reverse:
		var x = start.x
		start.x = goal.x
		goal.x = x
		
		var y = start.y
		start.y = goal.y
		goal.y = y
		
	var dx = goal.x - start.x
	var dy = abs(goal.y - start.y)
	var error = dx/2
	var ystep = 1 if start.y < goal.y else -1
	var y = start.y
	for x in range(start.x, goal.x+1):
		if steep:
			res.append(Vector2(y, x))
		else:
			res.append(Vector2(x, y))
		error -= dy
		if error < 0:
			y += ystep
			error += dx
	if reverse:
		res.invert()
	return res

И вот так это все работает:

Растеризация окружности осуществляется модифицированным алгоритмом брезенхема. К сожалению, хороших и простых статей на эту тему я не нашел, но она косвенно затрагивается в уже упомянутой выше статье. Стоит сказать, что моя реализация немного отличается. Кстати, вот она:

Окружность

func rast_circle(center:Vector2, radius:int) -> PoolVector2Array:
	var x:int = 0
	var y:int = radius
	var delta:int = 1-2*radius
	var error:int = 0
	var res:PoolVector2Array = []
	while y >= 0:
		if not center+Vector2(x, -y) in res:
			res.append(center+Vector2(x, -y))
		if not center+Vector2(-x, y) in res:
			res.append(center+Vector2(-x, y))
		if not center+Vector2(-x, -y) in res:
			res.append(center+Vector2(-x, -y))
		if not center+Vector2(x, y) in res:
			res.append(center+Vector2(x, y))
		error = 2*(delta+y)-1
		if delta < 0 and error <= 0:
			x += 1
			delta += 2*x+1
		elif delta > 0 and error > 0:
			y -= 1
			delta -= 2*y+1
		else:
			x += 1
			y -= 1
			delta += 2*(x-y)
	return res

Скорость у этой реализации я думаю далека от возможной, однако она меня еще не подводила. Вот пример работы:

Также оставлю здесь растеризацию эллипса. Если говорить честно, я уже не помню, что это за алгоритм и где я его взял, однако он очень похож на очередную модификация алгоритма Брезенхема. Его реализация:

Эллипс

func rast_ellipse(center:Vector2, size:Vector2):
	var res = PoolVector2Array([])
	var x = 0
	var y = size.y
	var a_sqr = size.x*size.x
	var b_sqr = size.y*size.y
	var delta = 4*b_sqr*(x+1)*(x+1) + a_sqr*(2*y-1)*(2*y-1) - 4*a_sqr*b_sqr
	while (a_sqr*(2*y-1) > 2*b_sqr*(x+1)):
		res.append(center+Vector2(x, y))
		res.append(center+Vector2(-x, y))
		res.append(center+Vector2(x, -y))
		res.append(center+Vector2(-x, -y))
		if delta < 0:
			x += 1
			delta += 4*b_sqr*(2*x+3)
		else:
			x += 1
			delta = delta-8*a_sqr*(y-1)+4*b_sqr*(2*x+3)
			y -= 1
	delta = b_sqr*(2*x+1)*(2*x+1)+4*a_sqr*(y+1)*(y+1)-4*a_sqr*b_sqr
	while y+1 != 0:
		res.append(center+Vector2(x, y))
		res.append(center+Vector2(-x, y))
		res.append(center+Vector2(x, -y))
		res.append(center+Vector2(-x, -y))
		if delta < 0:
			y -= 1
			delta += 4*a_sqr*(2*y+3)
		else:
			y -= 1
			delta -= 8*b_sqr*(x+1) + 4*a_sqr*(2*y+3)
			x += 1
			
	return res

Выглядит это как то так:

Заключение

Мне хочется верить в то, что данная тирада была вам интересна и полезна. Я постарался изложить как можно больше материала в форме картинок и анимаций, в надежде, что это поспособствует пониманию происходящего. Как возможный результат я сделал простенькую демку:

Назвать ее игрой язык не поворачивается, однако пару минут позабавиться можно. Скачать ее исходники, код реализации сеток всех трех видов и файл с алгоритмами можно здесь.

В целом я считаю тайловые миры идеальным выбором для инди разработки, ведь это минимальный источник багов и простой способ обустроить локацию. А с шестиугольными сетками, о которых поговорим в следующий раз, можно добиться потрясающего результата.

UPD: я уже выпустил статью про шестиугольные карты, там тоже много чего интересного.

UPD2: в качестве дополнения оставлю тут свой пост про алгоритм тайлового освещения, он отлично подойдет для создания т.н. поля видимости (Field of view) на тайлмапах.

Я благодарен вам за прочтение и желаю такой удачи, какой не желал еще никто!

Установка изометрического стиля сетки и шаговой привязки. AutoCAD 2009. Учебный курс

Читайте также

Создание сетки

Создание сетки Создание колоночной сетки (юниты) В книжном дизайне размер юнитов и колонок ограничен параметрами страницы. Окончательный размер печатной страницы, плаката или рекламного щита напрямую влияет на расчет сетки. В веб-дизайне окно браузера, самый близкий

Создание базовой сетки

Создание базовой сетки После того как мы создали колоночную сетку, можно перейти к созданию базовой сетки. Напомню, что базовая линия – это невидимая линия, на которой расположены буквы. Сетка образуется множеством базовых линий. Расстояние между линиями определяется

Сетки

Сетки • Der typografische raster. The Typographic Grid, Hans Rudolf Bosshard.• A Practical Guide to Designing Grid Systems for the Web, Mark Boulton.• Grid Systems: Principles of Organizing Type, Kimberly Elam.• Geometry of Design, Kimberly Elam (Элам К. Геометрия дизайна. Пропорции и композиция. СПб.: Питер, 2011).• The Grid Book, Hannah В. Higgins.• The Grid, Allen Hurlburt (Хёрлберт А. Сетка:

6.1. Масштабирование координатной сетки Y

6.1. Масштабирование координатной сетки Y Если при заданной частоте в рассматриваемой последовательной цепи наступает электрический резонанс, вы, как хороший знаток теории, естественно, ожидаете, что при этом напряжения на конденсаторе и на катушке индуктивности должны

Привязки

Привязки Суть действия привязок заключается в следующем. Система анализирует объекты, ближайшие к текущему положению указателя, чтобы определить их характерные точки (например, конец или центр отрезка, центр окружности, точку пересечения двух линий и т. п.) и затем

Определение параметров сетки

Определение параметров сетки Сеткой называется упорядоченная последовательность точек, покрывающих область рисунка в пределах лимитов. Работа в режиме GRID подобна наложению на рисунок листа бумаги в клетку. Использование сетки помогает выравнивать объекты и оценивать

Использование направляющих и сетки

Использование направляющих и сетки При работе мы можем использовать направляющие линии и сетки для большей точности (рис. 11.42). Их настройку мы рассматривали в главе 7, говоря о настройках программы. Рис. 11.42. Использование направляющих (слева) и сетки документа (справа) для

При помощи сетки

При помощи сетки Если требуется конструировать на плоскостях, отличных от основных сеток, или использовать одну и ту же плоскость во всех окнах проекций, то удобно применять объект Grid (Координатная сетка). Объекты сетки весьма полезны при увеличении сложности модели и

Редактируемые сетки (Editable Mesh)

Редактируемые сетки (Editable Mesh) Объекты Editable Mesh (Редактируемая сетка) имеют следующую сетчатую структуру (рис. 5.1): Рис. 5.1. Структура сетчатой поверхности, присваиваемой по умолчанию• Polygon (Полигон) – это многоугольник или замкнутая последовательность, состоящая из трех или

Привязки (Binders)

Привязки (Binders) Привязки bind1st и bind2nd берут функциональный объект f двух параметров и значение x и возвращают функциональный объект одного параметра, созданный из f с первым или вторым параметром соответственно, связанным с х.template ‹class Predicate›class binder1st: public unary_function {protected: Operation

Определение параметров сетки

Определение параметров сетки Сеткой называется упорядоченная последовательность точек, покрывающих область рисунка в пределах лимитов. Работа в режиме GRID подобна наложению на рисунок листа бумаги в клетку. Использование сетки помогает выравнивать объекты и оценивать

Определение параметров сетки

Определение параметров сетки Сеткой называется упорядоченная последовательность точек, покрывающих область рисунка в пределах лимитов. Работа в режиме GRID подобна наложению на рисунок листа бумаги в клетку. Использование сетки помогает выравнивать объекты и оценивать

Совмещение шаговой привязки с полярным отслеживанием

Совмещение шаговой привязки с полярным отслеживанием При использовании полярного отслеживания можно установить такой режим шаговой привязки, в котором узлы располагаются только вдоль линий полярного отслеживания через заданные интервалы.Для настройки шаговой

Определение параметров сетки

Определение параметров сетки Сеткой называется упорядоченная последовательность точек, покрывающих область рисунка в пределах лимитов. Работа в режиме GRID подобна наложению на рисунок листа бумаги в клетку. Использование сетки помогает выравнивать объекты и оценивать

Установка стиля

Установка стиля Прежде чем начать ввод текста, обратите внимание на текущие параметры текста, которые можно увидеть на панели форматирования: высоту и цвет пера. Они не совпадают с теми настройками, которые мы установили для технических требований. Дело в том, что окно

Касание сетки

Касание сетки Касание сеткиАвтор: Виктор ШепелевОпубликовано в журнале «Компьютерра» N25-26 от 08 июля 2008 годаОсенью прошлого года Adobe выпустила технологию Adobe AIR, связанную с ее (точнее, купленными у Macromedia) технологиями Flash и Flex. Примерно тогда же в свет вышла Silverlight — прямой

Изометрическая проекция

Во многих случаях используется изометрическая проекция: в компьютерных играх для трёхмерных объектов и панорам, в рисовании схем проезда и т.д. Рассмотрим, как можно рисовать изометрическую проекцию в Inkscape.

Для начала немного теории. Начнем с Википедии: Изометрическая проекция — это разновидность аксонометрической проекции, при которой в отображении трёхмерного объекта на плоскость коэффициент искажения (отношение длины спроектированного на плоскость отрезка, параллельного координатной оси, к действительной длине отрезка) по всем трём осям один и тот же. Слово «изометрическая» в названии проекции пришло из греческого языка и означает «равный размер», отражая тот факт, что в этой проекции масштабы по всем осям равны. По западным стандартам изометрическая проекция, помимо равенства масштабов по осям, включает условие равенства 120° углов между проекциями любой пары осей.

В прямоугольной изометрической проекции аксонометрические оси образуют между собой углы в 120°, ось Z’ направлена вертикально. Коэффициенты искажения (kx,ky,kz) имеют числовое значение . Как правило, для упрощения построений изометрическую проекцию выполняют без искажений по осям, то есть коэффициент искажения принимают равным 1, в этом случае получают увеличение линейных размеров в раза.

Изометрический вид объекта можно получить, выбрав направление обзора таким образом, чтобы углы между проекцией осей x, y, и z были одинаковы и равны 120°. К примеру, если взять куб, это можно выполнить направив взгляд на одну из граней куба, после чего повернув куб на ±45° вокруг вертикальной оси и на ±arcsin (tan 30°) = 35.264° вокруг горизонтальной оси. Обратите внимание: при изометрической проекции куба контур проекции образует правильный шестиугольник — все рёбра равной длины и все грани равной площади.

Подобным же образом изометрический вид может быть получен, к примеру, в редакторе трёхмерных сцен: начав с камерой, выровненной параллельно полу и координатным осям, её нужно повернуть вниз на =35.264° вокруг горизонтальной оси и на ±45° вокруг вертикальной оси.

Попробуем нарисовать предмет в изометрической проекции. Для опытов возьмём некий блочный предмет. Это может быть коробка, дом, книга, полка и т.п.

Описываемый здесь способ удобен, когда нужно нарисовать готовый объект с картинками и текстами в изометрической проекции, так как к этим элементам композиции также будут правильно применены операции масштабирования и сдвига.

Нарисуем развертку блочного элемента при помощи инструмента Rectangle, состоящую из трёх частей: передняя часть, боковая часть и верхняя часть.

Обратите внимание, что должны совпадать высоты передней и боковой части, а также ширина боковой и высота верхней части (в противном случае фигура просто не сложится). Размеры прямоугольников выберите по своему вкусу.

Мы не будем сейчас добавлять текст и другие элементы украшения, а сфокусируемся на технике создания изометрической проекции.

Для удобства можно раскрасить каждый прямоугольник блока в собственный цвет. Далее откройте диалоговое окно Fill and Stroke (Shift+Ctrl+F) и на вкладке Stroke style установите ширину границ в 1 пиксель.

При создании проекции каждая сторона меняет свои размеры (сужается) и сдвигается (искажается). А верхняя часть к тому же ещё и вращается. Делается это за несколько шагов.

Начнем с передней части. Выберите её при помощи инструмента Select. Далее вызовите диалоговое окно Transform через меню Object | Transform… (Shift+Ctrl+M). Перейдите на вкладку Scale и установите ширину прямоугольника в 86.603%, что эквивалентно cos(30°). Щелкните на кнопке Apply. После этой операции прямоугольник станет уже и изменит свое местоположение. Подвиньте его к остальным прямоугольникам.

Далее нам необходимо произвести операцию сдвига на 30°. Это легко сделать при помощи инструмента Select. Щёлкните на прямоугольнике два раза, чтобы включить режим поворота и сдвига. Когда вы это сделаете, то в центре фигуры увидите крестик — центр поворота. Вокруг этой точки осуществляется поворот фигуры или сдвига. Перетащите крестик в верхний правый угол прямоугольника. Будьте аккуратны и постарайтесь разместить крестик точно в указанном углу.

Теперь необходимо сделать сдвиг прямоугольника. Удерживая клавишу Ctrl, щёлкните и потащите стрелку сдвига на левой стороне прямоугольника. По умолчанию, при нажатой клавише Ctrl сдвиг происходит по шагам на 15°. Смотрите на строку состояния и сдвиньте прямоугольник на -30°

Повторите предыдущие шаги для боковой стороны. Измените ее ширину на 86.603% и сдвиньте на 30°. Единственная разница заключается в том, что центр поворота теперь нужно расположить в верхнем левом углу.

Финальная часть нашего упражнения — работа с верхним прямоугольником. Здесь есть свои особенности. Во-первых, для верхнего прямоугольника необходимо масштабировать не ширину (её оставляем равным 100%), а высоту на 86.603%. Во-вторых, для сдвига перемещаем центр поворота в нижний левый угол и сдвигаем на 30° (удерживаем клавишу Ctrl для аккуратного точного сдвига). Но это еще не всё. Далее берёмся за верхнюю левую стрелку и поворачиваем фигуру по часовой стрелке на 30°, опять удерживая клавишу Ctrl.

Если вы всё сделали правильно, то у вас получилась изометрическая проекция объекта.

Аксонометрическая сетка

В Inkscape есть специальная аксонометрическая сетка (File | Document Properties… | Вкладка Grids/Файл | Свойства документа | Сетки). В выпадающем списке выберите Axonometric grid. Использование аксонометрической сетки позволят создавать объекты в изометрии. Чтобы облегчить рисование ещё больше, можно также включить прилипание. Настройка сетки включает в себя изменения параметров единицы, основной линии и интервала по оси Y. Для большего удобства, можно также задать свои цвета основным и обычным линиям сетки.

Далее вы можете трансформировать объекты, как в верхнем примере, но при этом вам будет помогать сетка.

Общий алгоритм: Object | Transform…| Scale/Объект | Трансформировать | Масштаб, уменьшить ширину на 86,603%. Затем, в том же меню трансформации, следует изменить наклон по вертикали на 30 или −30 градусов (в зависимости от желаемого угла). Либо менять наклон вручную.

Создание параллелепипедов в 3D

С помощью инструмента «Рисовать параллелепипеды в 3D» (Shift+F4) можно создать объекты в изометрической проекции. Необходимо изменить направление точек схода всех трех углов от «конечных» до «бесконечных». А углы параллелепипеда установить в следующие значениях: X:150, Y:90, Z:30.

Чтобы редактировать цвет и обводку отдельной грани, не потеряв свойства трехмерного объекта, можно воспользоваться инструментом «Редактирования узлов и рычагов» (F2). На изображении — верхняя грань сделана прозрачной и стали видны внутренние стенки. А если уменьшить высоту стенок, то можно увидеть и дно.

Реклама

Изометрическая сетка

— простое руководство по ее созданию (2021 г.)

Знаете ли вы, что лучший способ создать впечатляющий шаблон — использовать изометрическое представление? Изометрическая сетка широко используется для создания впечатляющих трехмерных визуальных представлений, добавляющих нотку реализма.

Будете ли вы создавать изометрическую иллюстрацию или вектор. Сетки в основном используются для придания безупречной отделки 3D-объектам дизайна.

Сегодня мы узнаем о различных деталях об изометрических углах, шаблонах и о том, как создать сетку в Illustrator и Photoshop.Наряду с этим мы покажем вам идеи изометрического дизайна, которые заставят вас восхититься своим следующим дизайнерским проектом.

Что такое изометрическая сетка?

Это метод инженерного черчения, позволяющий получить трехмерный вид объектов. Чтобы нарисовать что-то с симметрией с трех сторон одновременно, нужна очень специфическая сетка. Это создает красивый однородный вид для объектов с трехмерной перспективой относительно инфографики.

Как создать изометрическую сетку?

Вы всегда хотели создать свой изометрический дизайн, но никогда не знали, с чего точно начать.Что ж, мы проведем вас через весь процесс создания системы сетки изометрической перспективы. Процесс создания изометрической сетки несложен. Вы можете начать с простой статьи.

Как нарисовать изометрическую сетку на бумаге

Во-первых, вы можете начать практиковаться или создавать изометрические объекты и рисовать сетку на миллиметровой бумаге. Вы можете легко найти шаблон миллиметровой бумаги формата А4 в Интернете, скачать его и распечатать. Для вашей помощи вот ссылка на PDF-файл. Также можно купить изометрическую записную книжку.

Сетка изометрической миллиметровой бумаги для печати

Сетка бумажная чертеж

Как создавать на бумаге карандашом и бумагой

Посмотрите это видео для быстрого старта.

Бесплатный иллюстратор изометрической сетки

Загрузить сейчас — Бесплатный файл иллюстраций, который пригодится при построении изометрических объектов.

Как создать изометрическую сетку в Photoshop и Illustrator

Это видео, приведенное ниже, объяснит весь процесс без особых хлопот, чтобы разработать его самостоятельно в Adobe Photoshop и Illustrator менее чем за 2 минуты.

Сетевой генератор

Как только вы начнете проектировать свои проекты в изометрической перспективе, вам это понравится все больше и больше. Однако вы можете упростить эту задачу с помощью лучших генераторов трехмерных перспективных сеток и завершить ее всего за несколько минут. Не забывайте, что существуют различные профессиональные инструменты, такие как Adobe Illustrator или Photoshop, которые облегчат вам эту задачу.

Представленный ниже лучший инструмент, используемый всеми дизайнерами, и вы бы поблагодарили нас за то, что поделились им с вами!

Изометрическая миллиметровка

Изометрическая миллиметровая бумага — это онлайн-инструмент для создания пользовательской сетки в соответствии с вашими требованиями в кратчайшие сроки.С помощью этого генератора изометрической миллиметровой бумаги вы можете настроить форматирование линий сетки, шаг сетки, размер бумаги, макет бумаги и распечатать его на обычной бумаге.

Мы переходим к заключительному разделу этого обсуждения, сюрприз! Да, у нас есть бонусы, готовые специально для вас!

Превосходный изометрический дизайн, который нельзя пропустить!

Мы создали эту коллекцию изометрических макетов и шаблонов, вдохновляющих вас на создание изометрических иллюстраций, рисунков и векторов.Наряду с этим эти сложные, но простые идеи помогут вам наилучшим образом отобразить дизайн или логотипы вашего веб-сайта, дизайн новых приложений, нестандартные конверты или визитки и т. Д.

Ниже приведен полный список примеров изометрического дизайна, который обогатит ваш творческий ум тонкими изометрическими рисунками:

Изометрический город Валида Бено

Timekit, иллюстрация Дмитрия Харченко

Аналитика данных Дмитрия Харченко

Часто задаваемые вопросы

Как создать изометрическую сетку в Photoshop?

Создать изометрическую сетку в Photoshop очень просто.Выше мы упомянули несколько простых руководств, с помощью которых вы можете легко это сделать. Вы также можете скачать PSD шаблон и использовать его в Photoshop.

Есть ли в Photoshop инструмент сетки?

Да, в Photoshop есть сетка-линейка или инструмент сетки, но это простая квадратная сетка, а не изометрия. Вот сочетание клавиш для отображения сетки в Photoshop. Нажмите [ Ctrl + ‘] или коснитесь, чтобы Просмотреть ⮞ Показать ⮞ Сетка .

Как сделать изометрическую сетку вручную?

Вы можете легко создавать сетки с помощью бумаги и карандаша.Выше мы уже упоминали туториал, с помощью которого вы можете сделать сетку вручную. Вы также можете скачать шаблон и распечатать его.

Несколько заключительных слов

Изометрическое проектирование — это новый оттенок, и люди влюбляются в эту тенденцию. Мало того, как только вы начнете использовать изометрическую сетку для своего дизайн-проекта, вы увидите, насколько красиво получаются ваши проекты. Испытайте магию изометрии в своих лучших проектах по дизайну приложений и веб-сайтов.

Сообщите нам, насколько вам понравилось использование изометрических сеток для веб-дизайна и других вещей, в разделе комментариев ниже.Мы надеемся, что вы остались довольны информацией, которой мы с вами поделились! Мы рады услышать от вас!

Раджиндер Сингх

https://thehotskills.com

Fountainhead of Thehotskills — Вдохновение в веб-дизайне и безмерное искусство — Ведущее агентство веб-дизайна, базирующееся в Чандигархе, предлагающее передовые UX / UI консультации и дизайн, индивидуальную сборку и оптимизированный для SEO веб-дизайн и разработку, а также услуги интерактивного цифрового дизайна продуктов. Посмотреть больше сообщений

Как создать изометрическую сетку в Adobe Illustrator | автор: Райан Аллен

Ссылки обновлены 3 мая 2021 г.

Следуйте за мной или поговорите со мной в Twitter, linkedin или dribble.

Мне нравится играть с изометрическими сетками, но я давно не создавал ничего с ними. Последнему проекту, который я сделал в этом стиле, довольно много лет, и я не мог найти свою изометрическую сетку. Пора сделать новый уууу!

Вот пошаговое руководство о том, как я сделал свой собственный. Если вы не хотите создавать свой собственный, вы можете скачать eps файла, который я собираюсь сделать здесь.

Создайте новый документ размером 5000 x 5000 пикселей. (Я делаю это в пикселях, а не в дюймах, потому что дюймы никогда не совпадают точно.Вещи всегда немного не в порядке).

Перейдите к своим общим настройкам (на Mac щелкните иллюстратор в верхнем меню / настройках / общих) и установите шаг клавиатуры на 100 пикселей ».

Выберите инструмент« Линия »и щелкните в любом месте монтажной области. Установите длину 6000 пикселей. и угол до 30 °. Переместите эту линию где-нибудь ближе к середине монтажной области, чтобы края немного свисали с правой и левой сторон.

Выберите линию. Удерживая нажатой опцию (alt на ПК), нажмите стрелку вниз на клавиатуре.Это продублирует линию и переместит ее на шаг 100 пикселей, который вы установили ранее. Сделайте это вниз на , а затем на вверх на , пока весь артборд не будет заполнен линиями под углом 30 °.

Затем выберите все строки с помощью command + a (control + a на компьютере) и перейдите к Object / Transform / Reflect.

Настройте отражение на вертикальной оси и щелкните по копии . Не нажимайте «ОК», так как это перевернет ваши строки, нажатие на «Копировать» дублирует строки и переворачивает дубликаты.

Далее проведем вертикальные линии. Чтобы сделать это, вернитесь в Preferences / General и установите шаг клавиатуры на 86.6px

Нам нужно превратить все наклонные линии, которые вы сделали, в направляющие. Выделите все с помощью command + a и нажмите command + 5, чтобы превратить их в направляющие (также в View> Guides> Make Guides).

Выберите инструмент «Линия» и щелкните в любом месте монтажной области (без перетаскивания). Установите длину 5000 пикселей, установите угол 90 ° и нажмите ОК.

Поместите линию где-нибудь около середины монтажной области и полностью увеличьте масштаб.Убедитесь, что у вас включены Snap to Point и Smart Guides (в меню View .

Мне проще выстроить это в виде схемы вместо предварительного просмотра, View / Outline или Command + y (любой еще помните, когда контурный вид был единственным способом работы в иллюстраторе?).

Совместите новую вертикальную линию с точками пересечения линий 30 °. Если вам не удается добиться идеальной привязки к тому месту, где вы хотите уменьшить масштаб, попробуйте совместить его с некоторыми точками в другой области монтажной области.Мне повезло расположить его на дальнем левом краю.

Аааааааааааааааааааааааааааа, идеально.

Нажмите Command + Y, чтобы вернуться в режим предварительного просмотра. Выберите вертикальную линию и, удерживая нажатой кнопку, нажмите стрелку вправо на клавиатуре, чтобы дублировать и переместить линию. Делайте это, пока не будет покрыт весь артборд.

Выбрать все (команда + a) и преобразовать новые строки в направляющие (команда + 5).

Пришло время для горизонтальных линий. Нарисуйте горизонтальную линию длиной около 5100 пикселей и совместите ее с пересечением линий под углом 30 °.

Нам нужно снова изменить шаг клавиатуры, на этот раз на 50 пикселей.

Дублируйте горизонтальные линии до тех пор, пока монтажная область не заполнится (удерживая нажатой опцию и щелкните вверх или вниз).

Теперь выберите все (команда + a) и превратите эти строки в направляющие (команда + 5).

Теперь у вас должен быть артборд, заполненный великолепной изометрической сеткой: D

Не стесняйтесь загружать .eps, которые я только что сделал, для использования во всем, что вы хотите. Делитесь своими достижениями, если вы этим гордитесь ☺ Подписывайтесь на меня или говорите со мной в твиттере.

Как играть с изометрической сеткой — Руководство для Roll20 и других VTT

Это руководство научит вас внедрять функциональную изометрическую сетку в Roll20, но теоретически вы можете использовать этот метод на любой виртуальной столешнице, которая поддерживает гексагональную сетку.

Прежде чем мы начнем, я хотел бы поблагодарить Rootyful, который первым поделился со мной этим методом, создал исходный оверлей и позволил мне передать его. Спасибо, Рути!

Шаг 1. Загрузите изометрические сетки

Я подготовил шесть оверлеев изометрической сетки, упакованных в PNG с прозрачным фоном.Эти плитки практически незаметны и предназначены для использования в качестве наложения на холст с разрешением 70 точек на дюйм. Подробнее об этом позже.

Загрузите ZIP-файл здесь.

Шаг 2. Подготовьте виртуальную столешницу

Создайте новую сцену (известную как «страница» в Roll20) и откройте ее настройки, щелкнув значок шестеренки в меню выбора страницы. Установите любые размеры, которые вам могут понадобиться, затем прокрутите вниз до раздела Grid и внесите следующие изменения:

• Установите сетку Тип на шестигранник (H).
• Установите ширину ячейки на 70 пикселей (по умолчанию).
• Установите для Grid Color и Opacity что-нибудь видимое. Это временно.

Шаг 3. Загрузите и выровняйте изометрическую сетку

Сначала переключитесь на слой «Карта и фон» , используя вертикальную панель инструментов в левой части экрана. Вы должны оставаться на этом слое, чтобы выбирать и управлять сеткой и всем остальным, что вы можете здесь разместить.

Затем импортирует изометрическую сетку по вашему выбору в сцену. Если вы впервые импортируете эту сетку в Roll20, просто перетащите файл PNG (из шага 1) по вашему выбору из браузера файлов в сцену Roll20. Если вы делали это ранее, лучше загрузить существующую сетку из Художественной библиотеки.

Изометрическая сетка теперь должна появиться в вашей сцене как объект, хотя вначале она, скорее всего, будет иметь очень странный масштаб.Щелкните его правой кнопкой мыши и выберите Advanced> Set Dimensions , затем введите 16 × 16 единиц (или 1120 × 1120 пикселей). Нажмите «Установить», чтобы подтвердить изменения.

Теперь сетка будет настроена на правильный масштаб, и вы сможете перемещать ее и привязать к шестиугольной сетке под ней. Он должен быть выровнен по сетке так:

Изометрическая сетка, размещенная поверх временной красной шестиугольной сетки.

Сохраните этот образ в памяти! Эта лежащая в основе шестнадцатеричная сетка позволит всем привязкам токенов, измерениям и всем другим инструментам на основе сетки работать с вашей новой изометрической сеткой.

Последний шаг — вернуться к настройкам страницы и установить для параметра Непрозрачность сетки значение 0, чтобы скрыть шестиугольную сетку . Ваша изометрическая сетка останется вместе со всеми базовыми функциями, и теперь вы можете скопировать и вставить плитку сетки 16 × 16 так, как вам угодно, чтобы заполнить сцену.

Вот и все! Просто не забудьте отправить свои боевые карты и активы за сетку на слое «Карты и фон», нажав «Правый щелчок»> «Назад», и используйте слой «Объекты и жетоны» для всего, что вы будете перемещать во время игры.

Если у вас есть какие-либо вопросы или комментарии, продолжайте прокрутку вниз и поделитесь ими ниже. Повеселись!

Изометрическая миллиметровая бумага для бесплатной печати

Изометрическая миллиметровая бумага для бесплатной печати

Реклама

Водонепроницаемая бумага

PuffinPaper
Водонепроницаемая бумага для лазерных принтеров
Водонепроницаемая бумага для струйных принтеров
Водонепроницаемая бумага для копировальных аппаратов
Водонепроницаемые тетради
Водонепроницаемые полевые книги
Водонепроницаемая бумага iGage
Rite-In-The-Rain Paper
Военная бумага
Буфер обмена для хранения
Водонепроницаемые ручки

Бесплатные распечатки

Бесплатные печатные формы
Бесплатные печатные календари
Бесплатная миллиметровая бумага
Бесплатные карты для печати
Бесплатные мишени для печати

Главная страница »Бесплатные печатные формы» Миллиметровая бумага для печати »Изометрическая миллиметровая бумага

Загрузите и распечатайте столько листов с изометрической графикой, сколько вам нужно

Если вы делаете перспективные иллюстрации зданий, продуктов или других объектов, лист бумаги с направляющими линиями значительно упрощает сохранение согласованной перспективы на всей иллюстрации.Вот почему многие художники используют изометрическую миллиметровку. Он представляет собой светлые линии, направляющие ваши рисунки. Мы предлагаем его с серыми или голубыми линиями, а также в портретном или альбомном формате. Эти удобные для печати листы можно использовать практически на любом компьютере и принтере с установленным Adobe Reader. Наслаждаться!

Изометрическая миллиметровая бумага — серый вертикальный треугольник

Изометрическая миллиметровая бумага — синий вертикальный треугольник

Изометрическая миллиметровая бумага — серый горизонтальный треугольник

Изометрическая миллиметровая бумага — синий горизонтальный треугольник
Загрузите их бесплатно.pdf и распечатайте свою собственную изометрическую миллиметровку, также известную как «бумага для трехмерного рисования». Вы можете использовать эти файлы бесплатно и распечатать столько листов, сколько захотите. Эта бумага используется многими людьми для создания перспективных чертежей зданий, коробок с продуктами и многого другого. Для облегчения работы с этими рисунками была добавлена ​​вертикальная направляющая.

Вся наша миллиметровая бумага для печати предназначена для печати на стандартном листе бумаги размером 8 1/2 x 11 дюймов. Это позволяет распечатать листы миллиметровой бумаги дома. Мы предоставим их вам в удобном для вас виде.pdf файлы, которые можно загрузить и которые надежны при печати. Они работают практически на любом принтере.

О нас, Доставка, Возврат, Доставка по почте, Политика конфиденциальности
© 2003-2021 WaterproofPaper.com. Все права защищены.
Изображения, текст и код на этом веб-сайте являются собственностью WaterproofPaper.com. Использование без разрешения запрещено.

Как создать изометрическую иллюстрацию

Среди множества стилей иллюстрации изометрические иллюстрации особенно выделялись в последние несколько лет своей уникальностью, которую они могут привнести в композицию.

Изометрическая иллюстрация или изометрическая проекция — это метод, предназначенный для создания иллюзии глубины и перспективы без искажения основных размеров объекта. Это проекция, в которой три оси координат (X, Y и Z) кажутся одинаково уменьшенными, а угол между двумя из любых осей всегда будет составлять 120 градусов (« изометрия » означает « такая же мера, » по-гречески) .

Другими словами, это простой способ представить трехмерный элемент с помощью двухмерной иллюстрации.Все три видимые стороны объекта представлены одинаково, с выделением, средним тоном и тенью в зависимости от направления света, создавая иллюзию глубины.

На экране приветствия Gravit Designer оставьте поля Ширина и Высота пустыми и нажмите « Создать! ”, чтобы создать бесконечный холст.

Если ничего не выбрано, вы можете увидеть параметры сетки в нижней части панели инспектора справа.Переключить Изометрическая сетка .

Изометрическая сетка Gravit может быть скорректирована по размеру и углам путем редактирования Размер , Угол 1 и Угол 2 .

Для этого урока оставим Размер на 5 , Угол 1 на 21 ° и Угол 2 на -21 ° .

Когда изометрическая сетка настроена, вы можете создать что-либо, следуя линиям сетки. В этом уроке давайте создадим гостиную.

Не забудьте переключить «Привязать к сетке» на Привязка параметры (щелкнув маленькую стрелку справа рядом со значком магнита) на панели инструментов. Возможно, вы захотите отключить параметры «Snap to Full Pixels» , «Snap to Shapes», и «Snap to Pages» для этой иллюстрации, так как вы не хотите, чтобы ваша привязка сходила с ума, фокусируясь только на сетки.

Начнем с создания стен. Выберите инструмент «Перо» «Перо» (P) и создайте прямоугольник, следующий за сеткой, чтобы этот прямоугольник находился в правильной перспективе.

Создайте вторую стену, а также пол с помощью инструмента «Перо», следуя той же перспективе. Добавьте немного цвета, но пока не беспокойтесь о выборе окончательной цветовой палитры.

Пора приступить к созданию некоторых деталей для гостиной, таких как окно и мебель. Вы можете проверить несколько изображений, чтобы понять, что создавать. Начните с добавления окна к левой стене с помощью инструмента «Перо».

Из-за перспективы иллюстрации вам нужно добавить иллюзию глубины большинству элементов.В случае окна это означает отображение внутренней части стены, которая будет видна внизу и с правой стороны.

Совет: изометрическую сетку не нужно постоянно включать. Если вы будете следовать своим основным линиям, вы получите правильный угол. Вы можете время от времени включать сетку в качестве ориентира для проверки наклона ваших путей.

Теперь давайте добавим диван. Этот диван представляет собой серию прямоугольников, следующих за сеткой и схемой выделения / полутона / тени, показанной ранее.

Установите диван правильно, как если бы он был спиной к стене гостиной. Вы можете добавить еще немного деталей, добавив к дивану деревянные ножки. Используя инструмент «Перо » , нарисуйте маленькие линии и установите концы на со скругленными углами в дополнительных настройках границы. Поместите эту небольшую дорожку позади формы дивана, чтобы казалось, что эта ступня идет из-под дивана.

Из-за перспективы левая ступня позади дивана не отображается на иллюстрации.

Теперь давайте добавим ковер и центральный стол. Снова с помощью инструмента «Перо» нарисуйте прямоугольник, изображающий ковер.

Поскольку предполагается, что ковер имеет некоторую глубину, добавьте два прямоугольника внизу, следуя тому же правилу прямоугольника, показывающего три стороны и выделение / полутона / тени.

Подобно ковру, центральный стол представляет собой другой прямоугольник с глубиной, но нижние прямоугольники, используемые для представления глубины, имеют большую высоту, чем прямоугольники, используемые для ковра.

Давайте добавим ножки к столу, расположенные за фигурой стола, и разместим все правильно на ковре. Вы также можете добавить детали к таблице, добавив еще один прямоугольник с другим цветом в его центре.

Как видите, большинство объектов можно составить из прямоугольников, следующих за линиями изометрической сетки.

Дальше, давайте построим телевизор и столик для него. Мы увидим заднюю часть телевизора, которая представляет собой еще один прямоугольник с меньшим прямоугольником, представляющим его опору.

У опоры будут закругленные концы, поэтому выберите ее с помощью инструмента Subselect (D), вы можете выбрать углы индивидуально и скруглить угол на панели инспектора.

Добавьте детали на заднюю панель телевизора, чтобы создать иллюзию глубины.

Телевизор будет стоять на столе, похожем на центральную часть, которую вы создали ранее, но немного более вытянутой. Ножки этого стола будут размещены над формой стола, чтобы придать дизайну дополнительную деталь.

Закругленные соединения деталей таблицы устанавливаются в дополнительных настройках границы, в том же месте, где вы ранее устанавливали закругленные концы пути.

Теперь, когда у вас есть некоторые основы гостиной, давайте начнем добавлять дополнительные детали, чтобы оживить эту иллюстрацию. Начните с добавления деталей на стену, например часов и картины.

Подобно ранее созданным фигурам, картина, висящая на стене, образована серией прямоугольников.

Добавьте что-нибудь на свою картину, чтобы сделать ее более живой.Давайте добавим форму сердца с помощью инструмента Bezigon (B).

Для получения дополнительных сведений об использовании инструмента Bezigon щелкните здесь .
Для любых объектов, которые не состоят из простых прямоугольников, вы можете использовать панель Transform , чтобы получить правильную перспективу.

Панель «Преобразование» имеет множество параметров, но в этом руководстве мы сосредоточимся на параметрах Skew . Выделив форму сердца, добавьте тот же угол, что и на изометрической сетке (21 градус) на Skew Y , и нажмите Apply .Это гарантирует, что ваш объект будет правильно искажен в соответствии с той же перспективой, которую вы используете для остальных элементов.

Тот же принцип может быть применен к любым другим объектам, поэтому, если у вас есть какие-либо элементы, которые труднее рисовать, только ориентируясь с помощью изометрической сетки, создайте элемент на обычном 2D-виде, а затем примените Наклон с правильным углом. сделать его изометрическим. Давайте воспользуемся этой техникой, чтобы добавить часы на стену.

Теперь добавим растения.Поскольку наши вазы и растения будут цилиндрическими, это означает, что их вид не нужно искажать, так как он уже будет выглядеть правильно на этом изометрическом виде.

Совет. Переключайтесь между изометрической сеткой и нормальной сеткой в ​​любое время на панели «Инспектор» в зависимости от ваших потребностей.

Начните с создания вазы для цветов с помощью простого прямоугольника. Преобразуйте его в путь на Щелкните правой кнопкой мыши> Преобразовать в путь и с помощью инструмента Subselect tool переместите узлы, чтобы сделать основание более узким, и потяните верхние узлы вниз, если вы хотите, чтобы ваза была короче.Снова используйте инструмент «Частичное выделение», чтобы растянуть контур внизу, создав кривую.

Сделайте аналогичный процесс, чтобы создать растение, похожее на сосну. Создайте прямоугольник и преобразуйте его в кривые, переместите узлы и сделайте углы скругленными под панелью «Оформление» .

Вы можете использовать ту же вазу для создания других видов растений, чтобы ваша гостиная выглядела более живо.

К центральному столу добавим книгу и кофейную кружку. Кофе, как и растения, имеет цилиндрическую форму, поэтому вы можете создать его в обычном 2D-виде и разместить на столе.
Вы можете создать кофейную кружку из простых прямоугольников и эллипсов, а ручку можно создать с помощью инструмента Bezigon .

Создайте небольшой дым, исходящий от кофе, с помощью инструмента «Перо» и установите для параметра «Непрозрачность » значение 25% на панели «Инспектор » .

Книгу можно создать с помощью прямоугольников, следующих по изометрической сетке.

Последняя деталь, которую мы добавим в эту гостиную, — это подушка на диване.Эту подушку необязательно делать из прямоугольников, и вы можете использовать инструмент «Перо » , чтобы создать что-то более округлое по линиям сетки.

При наличии источника света на иллюстрации всегда полезно добавлять тени, чтобы подчеркнуть иллюзию глубины объектов. Поскольку мы создаем источник света, идущий со стороны окна, тень должна быть на полу с противоположной стороны.

Тень будет блеклым цветом, исходящим от некоторых объектов с объемом, таких как столы, диван, вазы с растениями и предметы, висящие на стене.Ковер, например, является плоским элементом, поэтому в данном случае он не отбрасывает тени.
Тени могут быть созданы с помощью инструмента Pen или инструмента Ellipse для закругленных объектов и помещены за элементом, которому они принадлежат. Чтобы все тени были единообразными, используйте черный цвет с непрозрачностью 9% для всех теней.

Последняя деталь, которую мы добавим, — деревянный пол. Создайте серию прямоугольников, следующих за линиями сетки. Между каждым прямоугольником один путь более темного цвета, чтобы обозначить разделение между деревянными досками.

Теперь, когда вы закончили добавлять элементы к своим иллюстрациям, пора определить окончательные цвета. В этом примере я изменю цвета стен и некоторых других элементов, включая окно, сделав его ночным небом с некоторыми звездами.

Стены самого дома по-прежнему выглядят немного плоскими, поэтому мы добавим стенам глубины, как если бы мы действительно видели кусок, вырезанный из дома с настоящими трехмерными стенами. Чтобы создать этот эффект, создайте «бордюр» вокруг дома.

Эта граница представляет толщину стенки. Как и для всех прямоугольников, созданных ранее, верх — это свет, левый — средний тон, а правый — тень, поэтому просто создайте еще две формы, расположенные поверх последней.

Ваша изометрическая гостиная готова!

График 3 «x5» для заметок 3M Post It®, изометрическая сетка

График 3 «x5» для заметок 3M Post It®, изометрическая сетка

Магазин не будет работать корректно, если куки отключены.

Похоже, в вашем браузере отключен JavaScript. Для наилучшего взаимодействия с нашим сайтом обязательно включите Javascript в своем браузере.

• Дом
• Графика 3 «x5» для заметок 3M Post It®, изометрическая сетка

Изометрические графики 3 «x5» заметки Post-It ® идеально подходят для вашего класса математики! Эти липкие графические заметки позволяют учащимся легко рисовать диаграммы или точки.Студенты могут наклеивать записи в свои тетради или на стол во время лекций! Площадки для графиков имеют размер 3 «x5». В комплекте 3 подкладки по 100 листов.

• Изометрическая графическая сетка
  
• Идеальный интерактивный инструмент для занятий в классе.
• Размер 3 x 5 дюймов. По 3 прокладки в упаковке. 100 листов на блокнот.
• Клейкий стик легко удаляется в любом месте. 100% перерабатываемый материал.

Изометрические графики 3 «x5» заметки Post-It ® идеально подходят для вашего класса математики! Эти липкие графические заметки позволяют учащимся легко рисовать диаграммы или точки.Студенты могут наклеивать записи в свои тетради или на стол во время лекций! Площадки для графиков имеют размер 3 «x5». В комплекте 3 подкладки по 100 листов.

• Изометрическая графическая сетка
  
• Идеальный интерактивный инструмент для занятий в классе.
• Размер 3 x 5 дюймов. По 3 прокладки в упаковке. 100 листов на блокнот.
• Клейкий стик легко удаляется в любом месте. 100% перерабатываемый материал.

Дополнительная информация

Цвет	Белый с красными полосками
Страна производитель	США
Материал	Бумага
Размеры продукта	3×5
Безопасность	Нет опасности дросселирования
UPC	652012001652

об обновлениях и акциях

×

Глубокие пачки | Как создать изометрический текст и изометрическую сетку в иллюстраторе »Deep Tuts

---

Этот урок посвящен созданию изометрического текста и изометрической сетки в Adobe Illustrator.В учебнике есть точное соотношение значений поворота, сдвига и высоты, благодаря которым ваш объект преобразуется в правильное положение изометрии. Также через сетку в этом режиме можно начинать создавать объекты и формы.

Шаги по созданию графики

ИЗОМЕТРИЧЕСКИЙ ТЕКСТ | иллюстратор

Шаг 01 — Введите любой текст и преобразуйте этот текст в контур.

Шаг 02 — Используйте данные значения.

Высота — 86.602%

Сдвиг -30

повернуть 30

Изометрический текст готов

ИЗОМЕТРИЧЕСКАЯ СЕТКА | иллюстратор

Шаг 01 — Сделайте прямоугольную сетку из инструмента линии длительного нажатия.

Шаг 02 — Преобразуйте его в Guide и начните создавать объекты.

Готово, спасибо

Некоторые другие учебники по текстовым эффектам:
Учебник по текстовым эффектам (Adobe Illustrator) (Текстовый эффект 8)
Учебник по текстовым эффектам (Adobe Illustrator) (Текстовый эффект 7)
Учебник по текстовым эффектам (Adobe Illustrator) (Текстовый эффект 6)
Как использовать создать неоновый эффект в Adobe Illustrator
Как создать изометрический трехмерный текст или объект в Adobe Illustrator
Как создать линейный текст в Adobe Illustrator
Как создать эффект нарезанного текста в Adobe Illustrator

——————————-
Посмотрите это руководство на Youtube
https: // youtu.be / yj__qjnYePc
——————————-
☆☆☆ ПОДПИШИТЕСЬ на наш канал YouTube для получения дополнительных видеоуроков:
http://bit.ly/2Nmn2Dn
——————————— —
☆☆☆ ПОСМОТРЕТЬ больше видео и БЕСПЛАТНЫХ уроков:
http://bit.ly/2IXX4Sk
——————————-
Учебные плейлисты
Adobe Illustrator: http://bit.ly/2XlYP4I
Adobe Photoshop: http://bit.ly/2xo0bfu
——————————-
Подпишитесь, подписывайтесь и свяжитесь с нами на:
Facebook: https://www.facebook.com/deeptuts/
Instagram: https: // www.instagram.com/deeptuts/
Pinterest: https://in.pinterest.com/deeptuts/
Youtube: http://bit.ly/2IXX4Sk
Twitter: https://twitter.com/Deep_Tuts

Похожие сообщения

.