Векторная форма — Большая Энциклопедия Нефти и Газа, статья, страница 1
Векторная форма
Cтраница 1
Векторная форма, в которой были записаны уравнения неразрывности, движения и энергии, имеет перед скалярной преимущество в краткости записи и независимости от выбора системы координат. Однако при решении конкретных задач течения необходимо выбрать систему координат и определить в ней компоненты векторных и тензорных величин. Выбор системы координат зависит главным образом от геометрии границ жидкости, Так как наиболее часто используются прямоугольная. [1]
Векторная форма применима и для описания одномерной системы, в которую входят элементы с одним входом и одним выходом. [3]
Векторная форма является одной из графических методик представления хода технологического процесса. [4]
Векторная форма описания геометрических фигур
Эта векторная форма разложения используется затем при подстановке в уравнение Больцмана. [7]
В векторной форме двучленный закон выведен из теории размерностей в гл. [8]
В векторной форме уравнение (7.1) имеет универсальный вид во всех инер-циальных системах отсчета и не зависит от выбора начала координат. Предположим, что мы выбрали в качестве такового некоторую точку О. [9]
В векторной форме условие (1.29) применять для решения задач неудобно. [10]
В векторной форме условие ( 28) применять для решения задач неудобно. [11]
В векторной форме это можно изобразить так, как показано на рис. 8.4 а. Такое геометрическое представление сигналов позволяет легко понять, почему ФМн-сиг-нал с двумя значениями фазы оказывается наиболее помехоустойчивым. В том случае, когда область принятия решения состоит только из двух частей, вероятность ошибки наименьшая. [13]
В векторной форме эту систему можно записать так: v Аи, где матрица А а носит название матрицы технологических коэффициентов или матрицы технологических затрат. [14]
В векторной форме абсолютная нуль-система может быть записана в виде иАж, где А — кс-сосимметрич. [15]
Страницы: 1 2 3 4
www.ngpedia.ru
Декартова система
Декартова системаВ. Г. Автор. Векторная и тензорная алгебра для будущих физиков и техников
Суперобложка / Обложка / Содержание
Базис, состоящий из произвольной тройки некомпланарных векторов, принято называть произвольной косоугольной системой координат. Такая система неудобна для практических вычислений и не очень естественна. На практике никто не измеряет длину в метрах, ширину в дюймах, а высоту в лаптях. Если мы и пользуемся произвольной косоугольной системой координат, то эта мера вынужденная. Например, даже если мы свяжем с упругим телом какую-либо удобную для нас систему координат, то в процессе деформации упругого тела эта система, мягко говоря, покоробится. Есть проблемы, при изучении которых, мы принципиально не можем воспользоваться какой-либо специальной системой координат.
В тех случаях, когда обстоятельства позволяют, и задача этого требует, удобнее использовать некую специальную систему координат. Таких систем изобретено достаточно много: цилиндрическая, сферическая, полярная, эллиптическая и т.д. Очень часто оказывается удобна так называемая декартовая система координат.
Декартовой называется система, базисные векторы которой взаимно ортогональны, по модулю равны единице и образуют правую тройку. Обозначаются базисные векторы латинскими буквами, которые называются, в соответствии с традицией, по-французски: i – и, j – жи, k – ка (рис. 14).
Рис. 14Правил, позволяющих отличить правую тройку векторов от левой, имеется несколько. Из них наиболее часто используются четыре:
1. Правило левой руки.
Если кисть левой руки направить по направлению первого вектора и расположить ее так, чтобы второй вектор был направлен в ладонь, и если при этом большой палец левой руки будет направлен так же как третий вектор, то векторы образуют правую тройку векторов.
2. Правило правого винта.
Если первый вектор поворачивать по кратчайшему расстоянию в сторону второго, то третий вектор правой тройки векторов должен быть направлен в ту же сторону, в которую при таком вращении будет заворачиваться правый винт. Это правило на рис. 14 проиллюстрировано изображением спирали.
Остальные два правила не имеют названия.
3. Три вектора образуют правую тройку векторов, если при наблюдении из конца третьего вектора вращение первого по кратчайшему расстоянию в сторону второго происходит против часовой стрелки.
4. Если мы находимся внутри трехгранного угла, образованного тройкой векторов, и если при этом поворот от первого вектора ко второму, а затем к третьему должны выполнить против часовой стрелки, то векторы образуют правую тройку векторов.
Можно предложить и еще одно правило:
5. Векторы , и в указанном порядке образуют правую тройку векторов, если, будучи выстроенными в том же порядке друг за другом, они образуют правую спираль (рис. 15).
Рис. 15Вектор i (и) обычно совмещают с осью x, вектор j (жи) – с осью y, а вектор k (ка) – с осью z.
Поскольку базисные векторы декартовой системы координат взаимно ортогональны, то координаты произвольного вектора в такой системе совпадают с его ортогональными проекциями.
Пример обозначения координат произвольного вектора (рис. 14).
, ;
, ;
, .
Следовательно, в декартовой системе координат произвольный вектор может быть представлен в виде:
.
Модуль вектора , как видно из рис. 14, вычисляется как корень квадратный из суммы квадратов его координат: .
Если обозначить углы между вектором и векторами i, j и k соответственно , и , то разложение вектора по векторам базиса запишется так: или .
Вектор, совпадающий по направлению с вектором и имеющий единичную длину, называется направляющим вектором, или ортом-вектором, или просто ортом. Орт-вектор обозначается обычно с ноликом в правом верхнем углу: – орт-вектор вектора .
Так как
и , то
.
Косинусы в последнем выражении, которые являются координатами орта-вектора, называются направляющими косинусами.
Вектор, проведенный из начала координат в некоторую точку M, называется радиусом-вектором этой точки. Координаты точки (, и ) и координаты ее радиуса-вектора совпадают: .
Если нам заданы в пространстве две точки и , то координаты вектора можно вычислить, воспользовавшись тем, что
(рис. 16).
Рис. 16Выразив координаты радиусов-векторов через координаты точек, мы получим:
.
Следовательно, координаты вектора, проведенного из точки в A точку B, равны разности соответствующих координат этих точек.
.. Различные формы записи векторов
Принято различать координатную и векторную формы записи векторов. До сих пор мы пользовались только векторной формой записи. Но если мы выберем и зафиксируем в пространстве некоторую систему координат, то для задания любого вектора нам будет достаточно задать его координаты. Координаты, то есть три числа, взятые в определенном порядке, однозначно определяют вектор в выбранной системе координат. Поэтому можно записать: . Слева в этом равенстве стоит вектор, следовательно, под таблицей чисел, стоящей справа, необходимо понимать вектор с соответствующими координатами. Такая форма записи часто используется в векторной алгебре и называется координатной.
Таблицу можно записать по-разному, например так, как это принято в матричной алгебре: или .
Если под этими таблицами также понимать вектор с соответствующими координатами, то все эти таблицы представляют один и тот же вектор. Значит, мы имеем право записать:
.
Если рассматривать это равенство, как векторное, то его следует признать правильным. Однако, с точки зрения матричной алгебры, таблицы и представляют собой различные матрицы, и между ними не может быть поставлен знак равенства. Можно было бы проигнорировать эту проблему, поскольку матричная алгебра является самостоятельной наукой и, если не смешивать матричную и векторную алгебры, то недоразумений не возникает. Кроме того, никто не заставляет использовать матричный формат записи координат векторов. Общепринятой является форма записи координат векторов в фигурных скобках, которая не используется в теории матриц. Выходит, что, если ограничиться только общепринятой формой, то проблем не возникает. Но дело все в том, что матричная и векторная алгебры близки и по духу, и по решаемым проблемам. Когда дело доходит до реальных вычислений с векторами, полезно использовать матричные методы и обозначения. Короче говоря, матричную и векторную алгебры полезно максимально интегрировать. Для того, чтобы при этом возникало меньше проблем, мы слегка модернизируем обозначения:
1. Обозначение точек , или .
Точки будем обозначать большими буквами латинского алфавита. То, что обведено зеленоватым цветом, является необязательной частью обозначения. К необязательной части обозначения относится матрица с координатами точки.
Примеры: A, , .
2. Обозначение векторов
, , , .
Примеры: , , .
Кроме того, чтобы легче было переходить от векторов к матрицам и наоборот, введем знак «соответствия» «» – знак «равно» с точкой наверху. Этим знаком мы будем объединять одинаковые по смыслу векторные и матричные выражения, например,
.
Прочитать это выражение можно так: «Разнице векторов слева соответствует разность матриц справа».
Мы не будем давать точного определения для введенного нами знака «соответствия», рассматривая его в качестве «осторожного» знака равенства. Он должен напоминать, что хотя выражения, объединенные им, в известной степени, равны по смыслу, следует соблюдать осторожность при формальных преобразованиях.
..Линейные операции над векторами в координатной форме
Линейные операции над векторами можно выполнять как в векторной, так и в координатной формах, например:
1. Сложение векторов.
Векторная форма.
.
Координатная форма.
.
2. Умножение вектора на число.
Векторная форма.
.
Координатная форма.
.
rdt45m.narod.ru
Векторная форма — Энциклопедия по машиностроению XXL
Условие равновесия ползуна, записанное в векторной форме, будет [c.98]Если поверхность представлена уравнением и векторной форме R = R(u, v). lo построению каркаса должны предшествовать вычисления координат точек, принадлежащих данной поверхности. [c.90]
Условия равновесия системы сил в векторной форме [c.45]
Дифференциальное уравнение движения материальной точки под действием силы F можно представить в следующей векторной форме [c.214]
Дифференциальное уравнение движения материальной точки в векторной форме имеег вид [c.241]
V. = Vo, + — x + с уу + e,-z + 0)д V -В векторной форме (II) примет вид г = ( , + а)хл + (5 . [c.284]
После умножения обеих частей этого уравнения на массу ючки М и деления на d получаем следующее дифференциальное уравнение движения точки переменной массы в векторной форме [c.554]
Чтобы определить реакцию в среднем шарнире В, напишем в векторной форме условие равновесия сил для звена 2 [c.88]
Равенство (1) и определяет закон движения тачки в векторной форме, так как оно позволяет в любой момент времени построить соответствующий вектор г и найти положение движущейся точки. [c.97]
Уравнения (13) представляют собой дифференциальные уравнения движения системы в векторной форме (в них Сл=Уй=Гй). Входящие в правые части уравнений силы могут в общем случае зависеть от времени, координат точек системы и их скоростей. [c.273]
Уравнение (25) представляет собой в векторной форме дифференциальное уравнение движения точки переменной массы, называемое уравнением Мещерского. [c.288]
Сформулируйте теорему об измеиении количества движения мехаиической системы ири ударе в векторной форме и в проекциях на оси координат. [c.279]
В векторной форме теорема о моменте количества движения выражается так производная по времени от момента количества движения материальной точки относительно какого-либо неподвижного центра О равна моменту действующей силы относительно того же центра, т. е. [c.293]
Пусть, как и в предыдущем случае (см. 1.55), на точку действует система постоянных сил, равнодействующая которых Fst и ради упрощения рассуждений допустим, что силы действуют вдоль одной прямой. Тогда основному закону динамики в векторной форме эквивалентно равенство [c.142]
Здесь и ], к — орты (единичные векторы) осей координат. Если в (2 ) принять за X, у, X текущие координаты точки 7И, определяемые уравнениями (1 ), то (2 ) дает закон движения точки в векторной форме. [c.217]
Задача 330. По заданным в векторной форме уравнениям движения точки определить ее траекторию [c.133]
Есл движение точки задано уравнением в векторной форме [c.287]
Уравнение мгновенной винтовой оси. Уравнение мгновенной винтовой оси получим, исходя из того, что эта ось есть геометрическое место точек, направление скоростей которых в данный момент совпадает с направлением вектора ft). В векторной форме условие коллинеарности г и (й будет [c.158]
Это — условие равновесия в векторной форме. В проекциях на прямоугольные декартовы оси координат, т. е. в аналитической форме, условия равновесия, согласно (5), представляются в виде [c.192]
Равенство (9) выражает уравнение центральной оси в векторной форме, причем текущей координатой является вектор 00. [c.238]
Линия действия этой силы есть прямая, относительно всех точек О которой главный момент системы равен нулю, т. е. центральная ось системы уравнение ее в векторной форме есть уравнение (4). Заменяя в нем его значением из равенства (9), получим уравнение центральной оси в виде [c.244]
Условия равновесия плоской системы сил. В случае плоской системы сил условий равновесия в векторной форме будет также два, а именно [c.247]
Равенства (19) представляют собой известные из элементарной статики условия равновесия свободного абсолютно твердого тела в векторной форме. Заметим, что условия (19) необходимы для равновесия всякой системы материальных точек, потому что, предполагая эту систему отвердевшей, мы налагаем добавочные связи и не нарушаем равновесия системы, но достаточными эти условия будут только для абсолютно твердого тела. [c.302]
Равенство (1) выражает дифференциальное уравнение равновесия нити в векторной форме. [c.310]
Данный учебник отличается от аналогичных учебников бйльшим вниманием к современным способам формирования, задания и изображения поверхностей. Графическая информация о многих геометрических фигурах дополняется их уравнениями в векторной форме, позволяющими получить необходимые числовые характеристики о строении. линий и поверхностей. [c.2]
Можно получить уравнение прямой и векторной форме, если яланы ралиус-вектор ) олпой [c.25]
Выразим скорость, касательное, nopMajnjiioe и nojnioe ускорения точки тела в векторной форме. Скорость точки по модулю и направлению можно представить векторным произведением [c.142]
Переходя в уравнениях движения вязкой несжимаемой жидкосги (42) к безразмерным величинам и выразив для краткос 1и первые три уравнения в векторной форме, имеем [c.579]
Наблюдая пузыри различных форм, Маррей [564] изучал движение псевдоожиженных слоев и их устойчивость. Он показал, что псевдоожиженные слои неустойчивы по отношению к малым внутренним возмущениям и в общем случае устойчивы по отношению к малыш колебаниям поверхности. На основе наблюдаемых форм пузырей Маррей исследовал случай установившегося движения фаз, когда отношение плотностей твердой и жидкой фаз велико, т. е. Рр р, пренебрегая инерцией жидкой фазы. Уравнения (6.32), (6.33), (6.41), (6.42), (6.30) и (6.26) в векторной форме приобретают следующий вид [5651 [c.415]
Как формулируется теорема об н 1мснении кинетического момента механической системы в относительном движении по отношению к центру масс в векторной форме и в проекцлял на оси координат [c.241]
В векторной форме теорему о количестве движемия можно выразить двумя способами [c.280]
По отношению к системе отсчета Oxyz, движущейся произвольным образом относительно ииерциальнон системы O x y z, урав-пение движения материальной точки в векторной форме имеет вид [c.475]
Уравнения (1.36) огут быть записаны в векторной форме [c.22]
mash-xxl.info
Основные формы записи комплексных векторов
Рассмотрим запись комплексных векторов в показательной и алгебраической формах на комплексной плоскости в зависимости от угла и их величин.
В зависимости от угла , а следовательно его расположения в определенном квадранте, знаки действительной и мнимой части могут быть различными (рис. 3.43).
В I-м квадранте имеет место (рис. 3.43,а) и .
В II-м квадранте имеет место (рис. 3.43,б) и .
В III-м квадранте имеет место (рис. 3.43,в) и . Аргумент в третьем квадранте рационально записывать со знаком ” ”. В этом случае, вектор откладывается по часовой стрелке со знаком ”-”.
Например, комплексный вектор .
В IV-м квадранте имеет место (рис. 3.43,г) и . Аргумент в четвертом квадранте рационально записывать со знаком ” ”. В этом случае, вектор откладывается по часовой стрелке. Например, комплексный вектор .
В операциях с комплексными векторами используется понятие комплексно сопряженного вектора (рис. 3.44). Для комплексного вектора сопряженный комплексный вектор равен . Комплексно сопряженный вектор может быть получен в показательной форме из комплексного вектора путем замены знака аргумента на противоположный, либо заменой знака мнимой величины на противоположный в алгебраической форме.
Похожие статьи:
poznayka.org
Векторы и операции над векторами
Векторы занимают особое место среди объектов, рассматриваемых в высшей математике, поскольку каждый вектор имеет не только числовое значение — длину, но и физическое и геометрическое — направленность. Вектор, представленный направленным отрезком, идущим от точки A к точке B, обозначается так: .
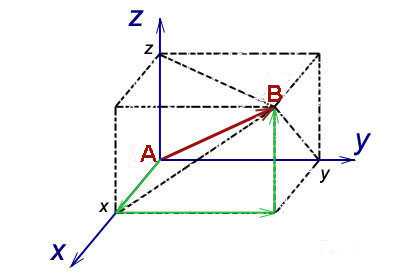
Вектор — это вид представления точки, до которой требуется добраться из некоторой начальной точки. Например, трёхмерный вектор, как правило, записывается в виде (х, y, z). Говоря совсем просто, эти числа означают, как далеко требуется пройти в трёх различных направлениях, чтобы добраться до точки.
Пусть дан вектор. При этом x = 3 (правая рука указывает направо), y = 1 (левая рука указывает вперёд), z = 5 (под точкой стоит лестница, ведущая вверх). По этим данным вы найдёте точку, проходя 3 метра в направлении, указываемом правой рукой, затем 1 метр в направлении, указываемом левой рукой, а далее Вас ждёт лестница и, поднимаясь на 5 метров, Вы, наконец, окажетесь в конечной точке.
Все остальные термины — это уточнения представленного выше объяснения, необходимые для различных операций над векторами, то есть, решения практических задач. Пройдёмся по этим более строгим определениям, останавливаясь на типичных задачах на векторы.
Физическими примерами векторных величин могут служить смещение материальной точки, двигающейся в пространстве, скорость и ускорение этой точки, а также действующая на неё сила.
Геометрический вектор представлен в двумерном и трёхмерном пространстве в виде направленного отрезка. Это отрезок, у которого различают начало и конец.
Если A — начало вектора, а B — его конец, то вектор обозначается символом или одной строчной буквой . На рисунке конец вектора указывается стрелкой (рис. 1)
Длиной (или модулем) геометрического вектора называется длина порождающего его отрезка
Два вектора называются равными, если они могут быть совмещены (при совпадении направлений) путём параллельного переноса, т.е. если они параллельны, направлены в одну и ту же сторону и имеют равные длины.
В физике часто рассматриваются закреплённые векторы, заданные точкой приложения, длиной и направлением. Если точка приложения вектора не имеет значения, то его можно переносить, сохраняя длину и направление в любую точку пространства. В этом случае вектор называется свободным. Мы договоримся рассматривать только свободные векторы.
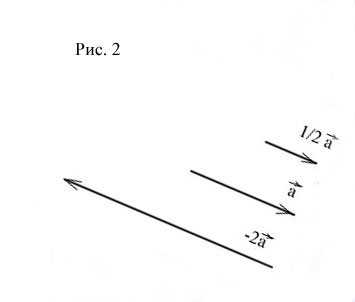
Умножение вектора на число
Сложение и вычитание векторов
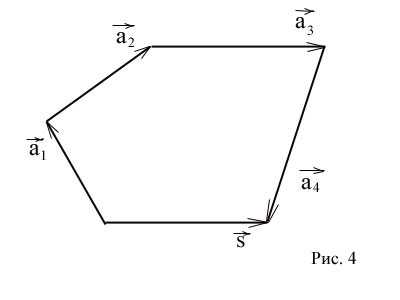
Слагаемые называются составляющими вектора , а сформулированное правило — правилом многоугольника. Этот многоугольник может и не быть плоским.
Пример 1. Упростить выражение:
.
Решение:
,
то есть, векторы можно складывать и умножать на числа так же, как и многочлены (в частности, также задачи на упрощение выражений). Обычно необходимость упрощать линейно подобные выражения с векторами возникает перед вычислением произведений векторов.
Пример 2. Векторы и служат диагоналями параллелограмма ABCD (рис. 4а). Выразить через и векторы , , и , являющиеся сторонами этого параллелограмма.
Решение. Точка пересечения диагоналей параллелограмма делит каждую диагональ пополам. Длины требуемых в условии задачи векторов находим либо как половины сумм векторов, образующих с искомыми треугольник, либо как половины разностей (в зависимости от направления вектора, служащего диагональю), либо, как в последнем случае, половины суммы, взятой со знаком минус. Результат — требуемые в условии задачи векторы:
Решить задачи на векторы самостоятельно, а затем посмотреть решения
Как найти длину суммы векторов?
Эта задача занимает особое место в операциях с векторами, так как предполагает использование тригонометрических свойств. Допустим, Вам попалась задача вроде следующей:
Даны длины векторов и длина суммы этих векторов . Найти длину разности этих векторов .
Решения этой и других подобных задач и объяснения, как их решать — в уроке «Сложение векторов: длина суммы векторов и теорема косинусов«.
А проверить решение таких задач можно на Калькуляторе онлайн «Неизвестная сторона треугольника (сложение векторов и теорема косинусов)».
А где произведения векторов?
Произведения вектора на вектор не являются линейными операциями и рассматриваются отдельно. И у нас есть уроки «Скалярное произведение векторов» и «Векторное и смешанное произведения векторов».
Проекция вектора на ось равна произведению длины проектируемого вектора на косинус угла между вектором и осью:
Как известно, проекцией точки A на прямую (плоскость) служит основание перпендикуляра , опущенного из этой точки на прямую (плоскость).
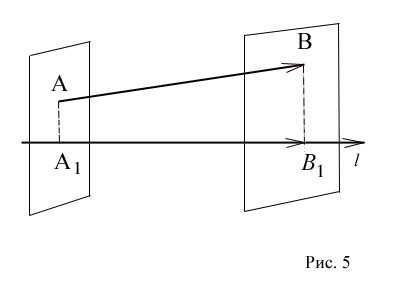
Пусть — произвольный вектор (Рис. 5), а и — проекции его начала (точки A) и конца (точки B) на ось l. (Для построения проекции точки A) на прямую проводим через точку A плоскость, перпендикулярную прямой. Пересечение прямой и плоскости определит требуемую проекцию.
Составляющей вектора на оси l называется такой вектор , лежащий на этой оси, начало которого совпадает с проекцией начала, а конец — с проекцией конца вектора .
Проекцией вектора на ось l называется число
,
равное длине составляющего вектора на этой оси, взятое со знаком плюс, если направление составляюшей совпадает с направлением оси l, и со знаком минус, если эти направления противоположны.
Основные свойства проекций вектора на ось:
1. Проекции равных векторов на одну и ту же ось равны между собой.
2. При умножении вектора на число его проекция умножается на это же число.
3. Проекция суммы векторов на какую-либо ось равна сумме проекций на эту же ось слагаемых векторов.
4. Проекция вектора на ось равна произведению длины проектируемого вектора на косинус угла между вектором и осью:
Пример 5. Рассчитать проекцию суммы векторов на ось l, если , а углы —
.
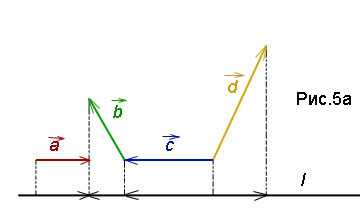
Решение. Спроектируем векторы на ось l как определено в теоретической справке выше. Из рис.5а очевидно, что проекция суммы векторов равна сумме проекций векторов. Вычисляем эти проекции:
Находим окончательную проекцию суммы векторов:
.
Знакомство с прямоугольной декартовой системой координат в пространстве состоялось в соответствующем уроке, желательно открыть его в новом окне.
В упорядоченной системе координатных осей 0xyz ось Ox называется осью абсцисс, ось 0y – осью ординат, и ось 0z – осью аппликат.
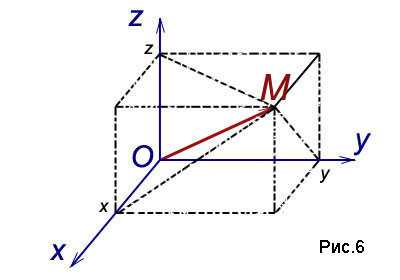
С произвольной точкой М пространства свяжем вектор
,
называемый радиус-вектором точки М и спроецируем его на каждую из координатных осей. Обозначим величины соответствующих проекций:
Числа x, y, z называются координатами точки М , соответственно абсциссой, ординатой и аппликатой, и записываются в виде упорядоченной точки чисел: M (x; y; z) (рис.6).
Вектор единичной длины, направление которого совпадает с направлением оси, называют единичным вектором(или ортом) оси. Обозначим через
Соответственно орты координатных осей Ox, Oy, Oz
Теорема. Всякий вектор может быть разложен по ортам координатных осей:
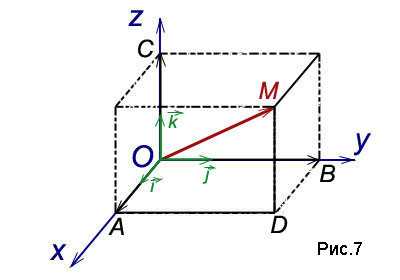
(2)
Равенство (2) называется разложением вектора по координатным осям. Коэффициентами этого разложения являются проекции вектора на координатные оси. Таким образом, коэффициентами разложения (2) вектора по координатным осям являются координаты вектора.
После выбора в пространстве определённой системы координат вектор и тройка его координат однозначно определяют друг друга, поэтому вектор может быть записан в форме
(3)
Представления вектора в виде (2) и (3) тождественны.
Как мы уже отмечали, векторы называются коллинеарными, если они связаны отношением
.
Пусть даны векторы . Эти векторы коллинеарны, если координаты векторов связаны отношением
,
то есть, координаты векторов пропорциональны.
Пример 6. Даны векторы . Коллинеарны ли эти векторы?
Решение. Выясним соотношение координат данных векторов:
.
Координаты векторов пропорциональны, следовательно, векторы коллинеарны, или, что то же самое, параллельны.
Вследствие взаимной перпендикулярности координатных осей длина вектора
равна длине диагонали прямоугольного параллелепипеда, построенного на векторах
и выражается равенством
(4)
Вектор полностью определяется заданием двух точек (начала и конца), поэтому координаты вектора можно выразить через координаты этих точек.
Пусть в заданной системе координат начало вектора находится в точке
а конец – в точке
(рис.8).
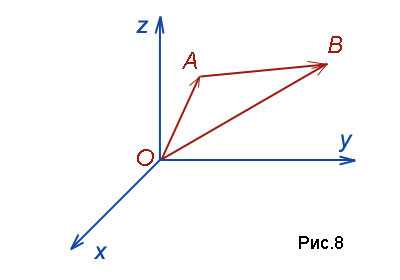
Тогда
Из равенства
следует, что
Отсюда
или в координатной форме
(5)
Следовательно, координаты вектора равны разностям одноимённых координат конца и начала вектора. Формула (4) в этом случае примет вид
(6)
Направление вектора определяют направляющие косинусы. Это косинусы углов, которые вектор образует с осями Ox, Oy и Oz. Обозначим эти углы соответственно α, β и γ. Тогда косинусы этих углов можно найти по формулам
,
,
.
Направляющие косинусы вектора являются также координатами орта этого вектора и, таким образом, орт вектора
или
.
Учитывая, что длина орта вектора равна одной единице, то есть
,
получаем следующее равенство для направляющих косинусов:
.
Пример 7. Найти длину вектора x = (3; 0; 4).
Решение. Длина вектора равна
Пример 8. Даны точки:
Выяснить, равнобедренный ли треугольник, построенный на этих точках.
Решение. По формуле длины вектора (6) найдём длины сторон и установим, есть ли среди них две равные:
Две равные стороны нашлись, следовательно необходимость искать длину третьей стороны отпадает, а заданный треугольник является равнобедренным.
Пример 9. Найти длину вектора и его направляющие косинусы, если .
Решение. Координаты вектора даны:
.
Длина вектора равна квадратному корню из суммы квадратов координат вектора:
.
Находим направляющие косинусы:
Решить задачу на векторы самостоятельно, а затем посмотреть решение
Пусть даны два вектора и , заданные своими проекциями:
или
или
Укажем действия над этими векторами.
1.Сложение:
или, что то же
(при сложении двух векторов одноимённые координаты складываются).
2.Вычитание:
или, что то же
,
(при вычитании двух векторов одноимённые координаты вычитаются).
3.Умножение вектора на число:
или, что то же
,
(при умножении вектора на число все координаты умножаются на это число).
Пример 11. Даны два вектора, заданные координатами:
.
Найти заданный координатами вектор, являющийся суммой этих векторов: .
Решение:
.
Решить задачи на координаты векторов самостоятельно, а затем посмотреть решение
При изучении многих вопросов, в частности, экономических, оказалось удобным обобщить рассмотренные приёмы установления соответствия между числами и точками двумерного и трёхмерного пространства и рассматривать последовательности n действительных чисел как «точки» некоторого абстрактного «n-мерного пространства», а сами числа — как «координаты» этих точек. За составляющие n-мерного вектора можно принимать такие данные, как урожайность различных культур, объёмы продаж товаров, технические коэффициенты, номенклатура товаров на складах и т.д.
n-мерным вектором называется упорядоченный набор из n действительных чисел, записываемых в виде
,
где - i – й элемент (или i – я координата) вектора x.
Возможна и другая запись вектора – в виде столбца координат:
Размерность вектора определяется числом его координат и является его отличительной характеристикой. Например, (2; 5) – двухмерный вектор, (2; -3; 0) – трёхмерный, (1; 3; -2; -4; 7) – пятимерный,
—
n – мерный вектор.
Нулевым вектором называется вектор, все координаты которого равны нулю:
0 = (0; 0; …; 0).
Введём операции над n-мерными векторами.
Произведением вектора
на действительное число называется вектор
(при умножении вектора на число каждая его координата умножается на это число).
Зная вектор
можно получить противоположный вектор
Суммой векторов
и
называется вектор
,
(при сложении векторов одной и той же размерности их соответствующие координаты почленно складываются).
Если в плане продаж сети торговых предприятий продажи товаров определить как положительные уровни товаров, а затраты на продажи – как отрицательные, то получим вектор затрат-продаж
,
где
—
продажи (затраты) k – м предприятием товара i, а k = 1, 2, 3,…, m .
Суммарный вектор затрат-продаж y определяется суммированием векторов затрат-продаж всех m предприятий сети:
Сумма противоположных векторов даёт нулевой вектор:
При вычитании двух векторов одной и той же размерности их соответствующие координаты почленно вычитаются:
Операции над n-мерными векторами удовлетворяют следующим свойствам.
Свойство 1.
Свойство 2.
Свойство 3.
Свойство 4.
Свойство 5.
Свойство 6.
Поделиться с друзьями
Весь блок «Аналитическая геометрия»
- Векторы
- Плоскость
- Прямая на плоскости
function-x.ru
20) Векторная форма представления синусоидальных величин
На декартовой плоскости из начала координат проводят векторы, равные по модулю амплитудным значениям синусоидальных величин, и вращают эти векторы против часовой стрелки (в ТОЭ данное направление принято за положительное) с угловой частотой, равнойw. Фазовый угол при вращении отсчитывается от положительной полуоси абсцисс. Проекции вращающихся векторов на ось ординат равны мгновенным значениям ЭДСе1ие2(рис. 3). Совокупность векторов, изображающих синусоидально изменяющиеся ЭДС, напряжения и токи, называютвекторными диаграммами. При построении векторных диаграмм векторы удобно располагать для начального момента времени(t=0), что вытекает из равенства угловых частот синусоидальных величин и эквивалентно тому, что система декартовых координат сама вращается против часовой стрелки со скоростьюw. Таким образом, в этой системе координат векторы неподвижны (рис. 4). Векторные диаграммы нашли широкое применение при анализе цепей синусоидального тока. Их применение делает расчет цепи более наглядным и простым. Это упрощение заключается в том, что сложение и вычитание мгновенных значений величин можно заменить сложением и вычитанием соответствующих векторов.
|
Пусть, например, в точке разветвления цепи (рис. 5) общий ток равен сумме токовидвух ветвей:
.
Каждый из этих токов синусоидален и может быть представлен уравнением
и.
Результирующий ток также будет синусоидален:
.
Определение амплитудыи начальной фазыэтого тока путем соответствующих тригонометрических преобразований получается довольно громоздким и мало наглядным, особенно, если суммируется большое число синусоидальных величин. Значительно проще это осуществляется с помощью векторной диаграммы. На рис. 6 изображены начальные положения векторов токов, проекции которых на ось ординат дают мгновенные значения токов дляt=0. При вращении этих векторов с одинаковой угловой скоростьюw их взаимное расположение не меняется, и угол сдвига фаз между ними остается равным.
Так как алгебраическая сумма проекций векторов на ось ординат равна мгновенному значению общего тока, вектор общего тока равен геометрической сумме векторов токов:
.
Построение векторной диаграммы в масштабе позволяет определить значенияииз диаграммы, после чего может быть записано решение для мгновенного значенияпутем формального учета угловой частоты: .
21) Представление синусоидальных величин в комплексной плоскости
Геометрические операции с векторами можно заменить алгебраическими операциями с комплексными числами, что существенно повышает точность получаемых результатов.
Каждому вектору на комплексной плоскости соответствует определенное комплексное число, которое может быть записано в :
показательной
тригонометрической или
алгебраической —формах.
Например, ЭДС , изображенной на рис. 7 вращающимся вектором, соответствует комплексное число
.
Фазовый угол определяется по проекциям вектора на оси “+1” и “+j” системы координат, как
.
В соответствии с тригонометрической формой записи мнимая составляющая комплексного числа определяет мгновенное значение синусоидально изменяющейся ЭДС:
, | (4) |
Комплексное число удобно представить в виде произведения двух комплексных чисел:
, | (5) |
Параметр , соответствующий положению вектора дляt=0 (или на вращающейся со скоростьюw комплексной плоскости), называюткомплексной амплитудой:, а параметр—комплексом мгновенного значения.
Параметр являетсяоператором поворотавектора на уголwt относительно начального положения вектора.
Вообще говоря, умножение вектора на оператор поворота есть его поворот относительно первоначального положения на угол±a.
Следовательно, мгновенное значение синусоидальной величины равно мнимой части без знака “j”произведения комплекса амплитудыи оператора поворота:
.
Переход от одной формы записи синусоидальной величины к другой осуществляется с помощью формулы Эйлера:
, | (6) |
Если, например, комплексная амплитуда напряжения задана в виде комплексного числа в алгебраической форме:
,
— то для записи ее в показательной форме, необходимо найти начальную фазу , т.е. угол, который образует векторс положительной полуосью +1:
.
Тогда мгновенное значение напряжения:
,
где .
При записи выражения для определенности было принято, что , т.е. что изображающий вектор находится в первом или четвертом квадрантах. Если, то при(второй квадрант)
, | (7) |
а при (третий квадрант)
(8) |
или
(9) |
Если задано мгновенное значение тока в виде , то комплексную амплитуду записывают сначала в показательной форме, а затем (при необходимости) по формуле Эйлера переходят к алгебраической форме:
.
Следует указать, что при сложении и вычитании комплексов следует пользоваться алгебраической формой их записи, а при умножении и делении удобна показательная форма.
Итак, применение комплексных чисел позволяет перейти от геометрических операций над векторами к алгебраическим над комплексами. Так при определении комплексной амплитуды результирующего тока по рис. 5 получим:
где ;
.
studfiles.net

