Комбинаторика: основные правила и формулы.
КОМБИНАТОРИКА
Комбинаторика – раздел математики, который изучает задачи выбора и расположения элементов из некоторого основного множества в соответствии с заданными правилами. Формулы и принципы комбинаторики используются в теории вероятностей для подсчета вероятности случайных событий и, соответственно, получения законов распределения случайных величин. Это, в свою очередь, позволяет исследовать закономерности массовых случайных явлений, что является весьма важным для правильного понимания статистических закономерностей, проявляющихся в природе и технике.
Правила сложения и умножения в комбинаторике
Правило суммы. Если два действия А и В взаимно исключают друг друга, причем действие А можно выполнить m способами, а В – n способами, то выполнить одно любое из этих действий (либо А, либо В) можно n + m способами.
Пример 1.
В классе учится 16 мальчиков и 10 девочек. Сколькими способами можно назначить одного дежурного?
Решение
Дежурным можно назначить либо мальчика, либо девочку, т.е. дежурным может быть любой из 16 мальчиков, либо любая из 10 девочек.
По правилу суммы получаем, что одного дежурного можно назначить 16+10=26 способами.
Правило произведения. Пусть требуется выполнить последовательно k действий. Если первое действие можно выполнить n1 способами, второе действие n2 способами, третье – n3 способами и так до k-го действия, которое можно выполнить nk способами, то все k действий вместе могут быть выполнены:
способами.
Пример 2.
В классе учится 16 мальчиков и 10 девочек. Сколькими способами можно назначить двух дежурных?
Решение
Первым дежурным можно назначить либо мальчика, либо девочку. Т.к. в классе учится 16 мальчиков и 10 девочек, то назначить первого дежурного можно 16+10=26 способами.
После того, как мы выбрали первого дежурного, второго мы можем выбрать из оставшихся 25 человек, т.е. 25-ю способами.
По теореме умножения двое дежурных могут быть выбраны 26*25=650 способами.
Сочетания без повторений. Сочетания с повторениями
Классической задачей комбинаторики является задача о числе сочетаний без повторений, содержание которой можно выразить вопросом:
Пример 3.
Необходимо выбрать в подарок 4 из 10 имеющихся различных книг. Сколькими способами можно это сделать?
Решение
Нам из 10 книг нужно выбрать 4, причем порядок выбора не имеет значения. Таким образом, нужно найти число сочетаний из 10 элементов по 4:
.
Рассмотрим задачу о числе сочетаний с повторениями: имеется по r одинаковых предметов каждого из n различных типов; сколькими способами
.
Пример 4.
В кондитерском магазине продавались 4 сорта пирожных: наполеоны, эклеры, песочные и слоеные. Сколькими способами можно купить 7 пирожных?
Решение
Т.к. среди 7 пирожных могут быть пирожные одного сорта, то число способов, которыми можно купить 7 пирожных, определяется числом сочетаний с повторениями из 7 по 4.
.
Размещения без повторений. Размещения с повторениями
Классической задачей комбинаторики является задача о числе размещений без повторений, содержание которой можно выразить вопросом:
Пример 5.
В некоторой газете 12 страниц. Необходимо на страницах этой газеты поместить четыре фотографии. Сколькими способами можно это сделать, если ни одна страница газеты не должна содержать более одной фотографии?
Решение.
В данной задаче мы не просто выбираем фотографии, а размещаем их на определенных страницах газеты, причем каждая страница газеты должна содержать не более одной фотографии. Таким образом, задача сводится к классической задаче об определении числа размещений без повторений из 12 элементов по 4 элемента:
Таким образом, 4 фотографии на 12 страницах можно расположить 11880 способами.
Также классической задачей комбинаторики является задача о числе размещений с повторениями, содержание которой можно выразить вопросом: сколькими способами можно выбрать и разместить по m различным местам m из n предметов, среди которых есть одинаковые?
Пример 6.
У мальчика остались от набора для настольной игры штампы с цифрами 1, 3 и 7. Он решил с помощью этих штампов нанести на все книги пятизначные номера– составить каталог. Сколько различных пятизначных номеров может составить мальчик?
Решение
Можно считать, что опыт состоит в 5-кратном выборе с возращением одной из 3 цифр (1, 3, 7). Таким образом, число пятизначных номеров определяется числом размещений с повторениями из 3 элементов по 5:
.
Перестановки без повторений. Перестановки с повторениями
Классической задачей комбинаторики является задача о числе перестановок без повторения, содержание которой можно выразить вопросом:
Пример 7.
Сколько можно составить четырехбуквенных «слов» из букв слова«брак»?
Решение
Генеральной совокупностью являются 4 буквы слова «брак» (б, р, а, к). Число «слов» определяется перестановками этих 4 букв, т. е.
Для случая, когда среди выбираемых n элементов есть одинаковые (выборка с возвращением), задачу о числе перестановок с повторениями можно выразить вопросом: сколькими способами можно переставить n предметов, расположенных на n различных местах, если среди n предметов имеются k различных типов (k < n), т. е. есть одинаковые предметы.
Пример 8.
Сколько разных буквосочетаний можно сделать из букв слова «Миссисипи»?
Решение
Здесь 1 буква «м», 4 буквы «и», 3 буквы «c» и 1 буква «п», всего 9 букв. Следовательно, число перестановок с повторениями равно
ОПОРНЫЙ КОНСПЕКТ ПО РАЗДЕЛУ «КОМБИНАТОРИКА»
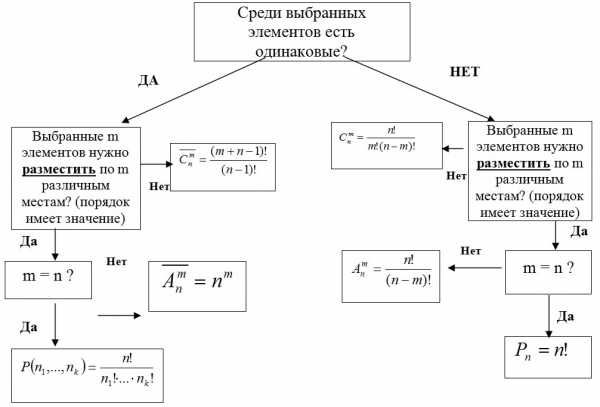
ya-znau.ru
Комбинаторика. Размещения, перестановки, сочетания | Математика, которая мне нравится
В комбинаторике изучают вопросы о том, сколько комбинаций определенного типа можно составить из данных предметов (элементов).
Рождение комбинаторики как раздела математики связано с трудами Б. Паскаля и П. Ферма по теории азартных игр. Большой вклад в развитие комбинаторных методов внесли Г.В. Лейбниц, Я. Бернулли и Л. Эйлер.
Французский философ, писатель, математик и физик Блез Паскаль (1623–1662) рано проявил свои выдающиеся математические способности. Круг математических интересов Паскаля был весьма разнообразен. Паскаль доказал одну
из основных теорем проективной геометрии (теорема Паскаля), сконструировал суммирующую машину (арифмометр Паскаля), дал способ вычисления биномиальных коэффициентов (треугольник Паскаля), впервые точно определил и применил для доказательства метод математической индукции, сделал существенный шаг в развитии анализа бесконечно малых, сыграл важную роль в зарождении теории вероятности. В гидростатике Паскаль установил ее основной закон (закон Паскаля). “Письма к провинциалу” Паскаля явились шедевром французской классической прозы.
Готфрид Вильгельм Лейбниц (1646–1716) — немецкий философ, математик, физик и изобретатель, юрист, историк, языковед. В математике наряду с И. Ньютоном разработал дифференциальное и интегральное исчисление. Важный вклад внес в комбинаторику. С его именем, в частности, связаны теоретико-числовые задачи.
Готфрид Вильгельм Лейбниц имел мало внушительную внешность и поэтому производил впечатление довольно невзрачного человека. Однажды в Париже он зашел в книжную лавку в надежде приобрести книгу своего знакомого философа. На вопрос посетителя об этой книге книготорговец, осмотрев его с головы до ног, насмешливо бросил: “Зачем она вам? Неужели вы способны читать такие книги?” Не успел ученый ответить, как в лавку вошел сам автор книги со словами: “Великому Лейбницу привет и уважение!” Продавец никак не мог взять втолк, что перед ним действительно знаменитый Лейбниц, книги которого пользовались большим спросом среди ученых.
В дальнейшем важную роль будет играть следующая
Лемма.
Доказательство. Действительно, с одним элементом из множества мы можем составить таких различных пар, а всего в множестве элементов.
Размещения, перестановки, сочетания
Пусть у нас есть множество из трех элементов . Какими способами мы можем выбрать из этих элементов два? .
Определение. Размещениями множества из различных элементов по элементов называются комбинации, которые составлены из данных элементов по > элементов и отличаются либо самими элементами, либо порядком элементов.
Число всех размещений множества из элементов по элементов обозначается через (от начальной буквы французского слова “arrangement”, что означает размещение), где и .
Теорема. Число размещений множества из элементов по элементов равно
Доказательство. Пусть у нас есть элементы . Пусть — возможные размещения. Будем строить эти размещения последовательно. Сначала определим — первый элемент размещения. Из данной совокупности элементов его можно выбрать различными способами. После выбора первого элемента для второго элемента остается способов выбора и т.д. Так как каждый такой выбор дает новое размещение, то все эти выборы можно свободно комбинировать между собой. Поэтому имеем:
Пример. Сколькими способами можно составить флаг, состоящий из трех горизонтальных полос различных цветов, если имеется материал пяти цветов?
Решение. Искомое число трехполосных флагов:
Определение. Перестановкой множества из элементов называется расположение элементов в определенном порядке.
Так, все различные перестановки множества из трех элементов — это
Очевидно, перестановки можно считать частным случаем размещений при >.
Число всех перестановок из элементов обозначается (от начальной буквы французского слова “permutation”, что значит “перестановка”, “перемещение”). Следовательно, число всех различных перестановок вычисляется по формуле
Пример. Сколькими способами можно расставить ладей на шахматной доске так, чтобы они не били друг друга?
Решение. Искомое число расстановки ладей
по определению!
Определение. Сочетаниями из различных элементов по элементов называются комбинации, которые составлены из данных элементов по элементов и отличаются хотя бы одним элементом (иначе говоря, -элементные подмножества данного множества из элементов).
Как видим, в сочетаниях в отличие от размещений не учитывается порядок элементов. Число всех сочетаний из элементов по элементов в каждом обозначается (от начальной буквы французского слова “combinasion”, что значит “сочетание”).
Числа
Все сочетания из множества по два — .
.
Свойства чисел {\sf C}_n^k
1. .
Действительно, каждому -элементному подмножеству данного -элементного множества соответствует одно и только одно -элементное подмножество того же множества.
2. .
Действительно, мы можем выбирать подмножества из элементов следующим образом: фиксируем один элемент; число -элементных подмножеств, содержащих этот элемент, равно ; число -элементных подмножеств, не содержащих этот элемент, равно .
Треугольник Паскаля
В этом треугольнике крайние числа в каждой строке равны 1, а каждое не крайнее число равно сумме двух чисел предыдущей строки, стоящих над ним. Таким образом, этот треугольник позволяет вычислять числа .

.
Теорема.
Доказательство. Рассмотрим множество из элементов и решим двумя способами следующую задачу: сколько можно составить последовательностей из элементов данного
множества, в каждой из которых никакой элемент не встречается дважды?
1 способ. Выбираем первый член последовательности, затем второй, третий и т.д. член
2 способ. Выберем сначала элементов из данного множества, а затем расположим их в некотором порядке
Домножим числитель и знаменатель этой дроби на :
Пример. Сколькими способами можно в игре “Спортлото” выбрать 5 номеров из 36?
Искомое число способов
Задачи.
1. Номера машин состоят из 3 букв русского алфавита (33 буквы) и 4 цифр. Сколько существует различных номеров автомашин?
2. На рояле 88 клавиш. Сколькими способами можно извлечь последовательно 6 звуков?
3. Сколько есть шестизначных чисел, делящихся на 5?
4. Сколькими способами можно разложить 7 разных монет в три кармана?
5. Сколько можно составить пятизначных чисел, в десятичной записи которых хотя бы один раз встречается цифра 5?
6. Сколькими способами можно усадить 20 человек за круглым столом, считая способы одинаковыми, если их можно получить один из другого движением по кругу?
7. Сколько есть пятизначных чисел, делящихся на 5, в записи которых нет одинаковых цифр?
8. На клетчатой бумаге со стороной клетки 1 см нарисована окружность радиуса 100 см, не проходящая через вершины клеток и не касающаяся сторон клеток. Сколько клеток может пересекать эта окружность?
9. Сколькими способами можно расставить в ряд числа так, чтобы числа стояли рядом и притом шли в порядке возрастания?
10. Сколько пятизначных чисел можно составить из цифр , если каждую цифру можно использовать только один раз?
11. Из слова РОТ перестановкой букв можно получить еще такие слова: ТОР, ОРТ, ОТР, ТРО, РТО. Их называют анаграммами. Сколько анаграмм можно составить из слова ЛОГАРИФМ?
12. Назовем разбиением натурального числа представление его в виде суммы натуральных чисел. Вот, например, все разбиения числа :
Разбиения считаются разными, если они отличаются либо числами, либо порядком слагаемых.
Сколько существует различных разбиений числа на слагаемых?
13. Сколько существует трехзначных чисел с невозрастающим порядком цифр?
14. Сколько существует четырехзначных чисел с невозрастающим порядком цифр?
15. Сколькими способами можно рассадить в ряд 17 человек, чтобы и оказались рядом?
16. девочек и мальчиков рассаживаются произвольным образом в ряду из мест. Сколькими способами можно их рассадить так, чтобы никакие две девочки не сидели рядом?
17. девочек и мальчиков рассаживаются произвольным образом в ряду из мест. Сколькими способами можно их рассадить так, чтобы все девочки сидели рядом?
hijos.ru
Свойства сочетаний.
1) 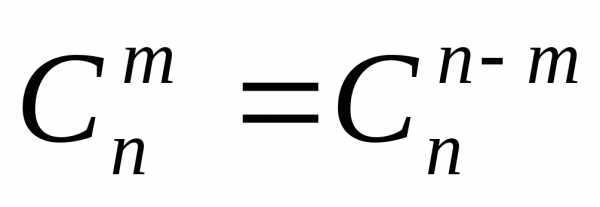 (1.8)
(1.8)
Действительно,
2) (1.9)
Покажем, что правая часть (1.9) равна левой части (1.9)
3) (1.10)
В соответствии с формулой бинома Ньютона
Пример 1. 10.
Сколькими способами можно составить дозор из трех солдат, если на заставе 20 солдат.
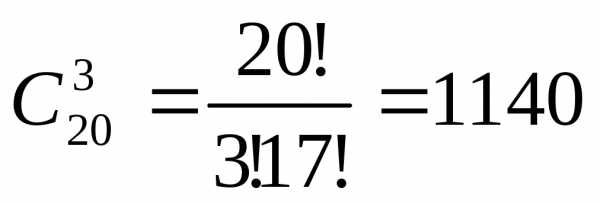
Пример 1.11.
В полуфинале первенства страны по шахматам участвуют 20 чел. В финал выходят трое. Найти число различных исходов полуфинала шахматного первенства.
Здесь нас не интересует порядок, в котором располагается первая тройка. Поэтому число исходов
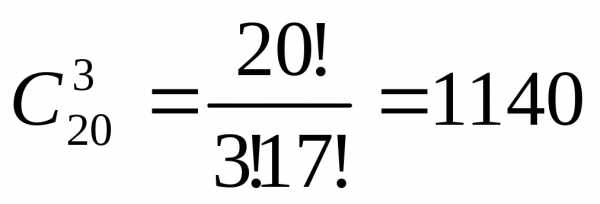
Пример 1.12.
В турнире участвуют 8 игроков. Из трех человек, занявших первые места, формируется команда для поездки на соревнование. Каким количеством способов может быть сформирована команда?
Вопрос сводится к следующему: каким количеством способов можно выбрать трех человек из восьми? (порядок выбора роли не играет) По определению – это число сочетаний из восьми по три:
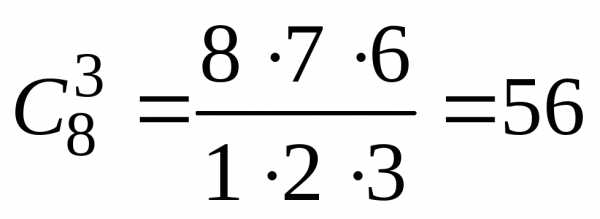 .
.
Пример 1.13.
В магазине 12 сортов пирожных. Покупатель хочет купить шесть разных пирожных. Сколько вариантов выбора у него есть?
Решение
Количество способов выбора здесь
.
В последнем примере было поставлено ограничение – разные пирожные. Если же ограничение снять, то количество вариантов выбора возрастет. Для того чтобы подсчитать количество способов выбора шести любых пирожных из 12 сортов (количество пирожных каждого сорта полагается неограниченным), нужно ввести еще одно определение – сочетание с повторениями.
Рассмотрим
неограниченное количество предметов 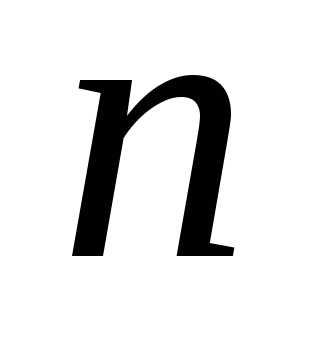 различных сортов. Пусть предметы одного
сорта не различаются.
различных сортов. Пусть предметы одного
сорта не различаются.
Сочетания с повторениями
Сочетанием
с повторениями из 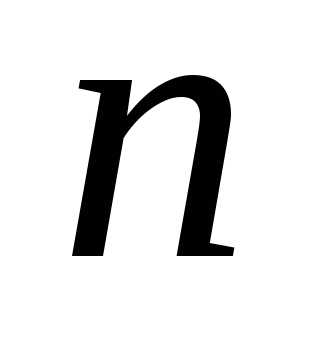 элементов по
элементов по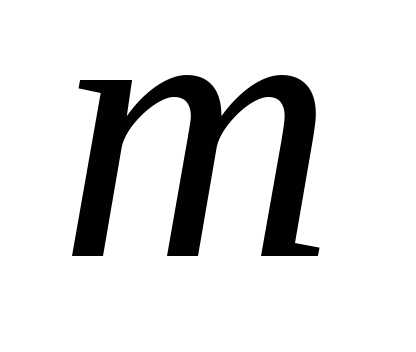 называется
выборка
называется
выборка 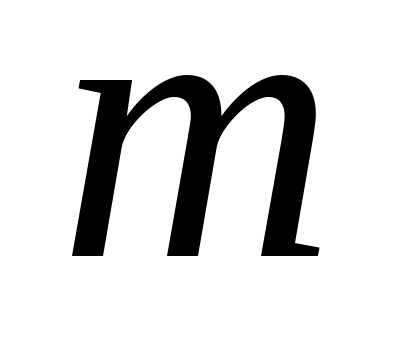 предметов из неограниченного количества
предметов
предметов из неограниченного количества
предметов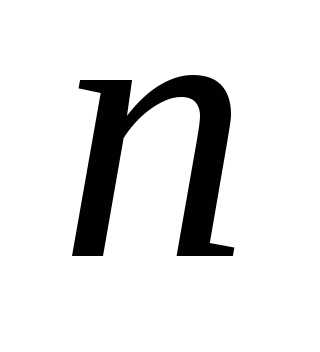 различных сортов. Такие выборки должны
отличаться хотя бы одним элементом,
т.е. порядок элементов во внимание не
принимается
различных сортов. Такие выборки должны
отличаться хотя бы одним элементом,
т.е. порядок элементов во внимание не
принимается
Число
вариантов выбора или количество таких
сочетаний обычно обозначается 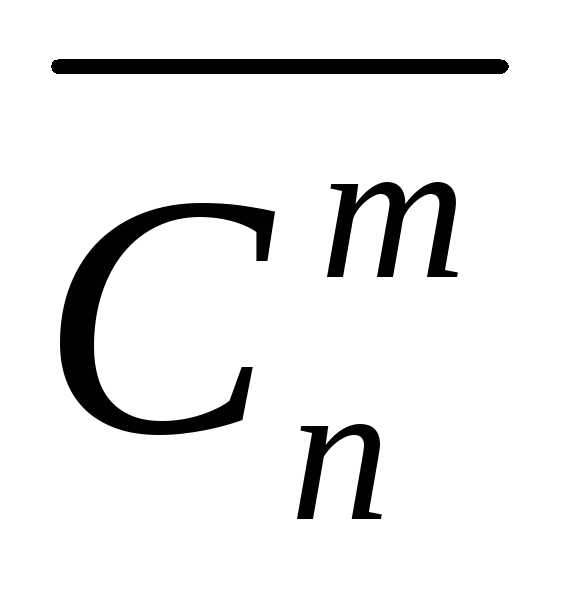 и вычисляется по формуле
и вычисляется по формуле
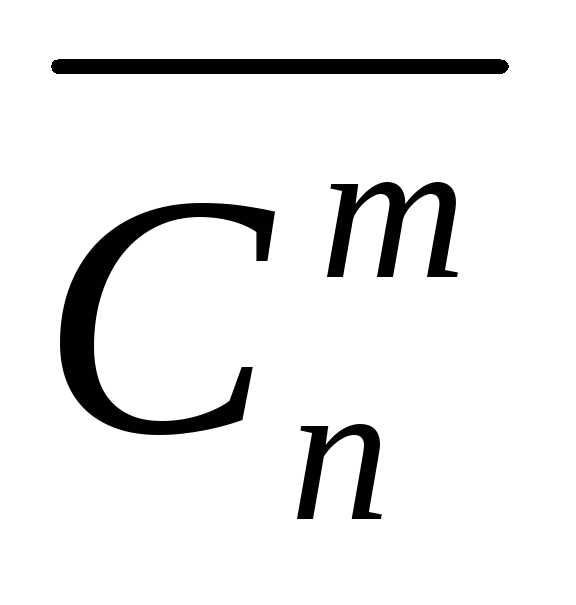 .
(1.11)
.
(1.11)
Каждое
сочетание полностью определяется , если
указать, сколько элементов каждого из 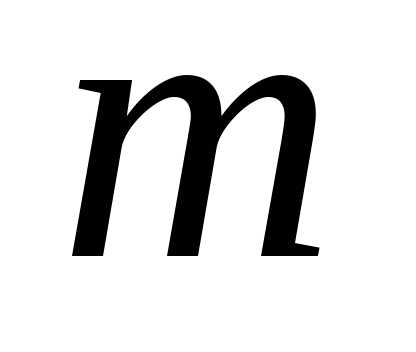 типов в него входит. Назовем кратностью
элемента число повторений данного
элемента в сочетании с повторениями.
Например, в сочетанииэлемент
типов в него входит. Назовем кратностью
элемента число повторений данного
элемента в сочетании с повторениями.
Например, в сочетанииэлемент имеет кратность
имеет кратность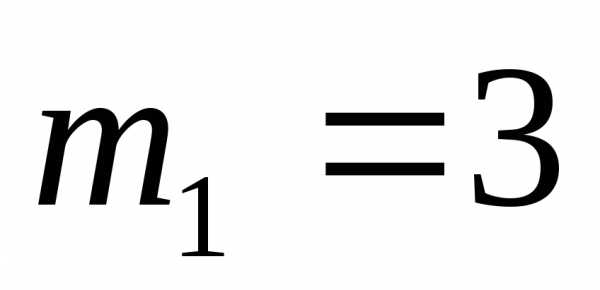 ,
элемент
,
элемент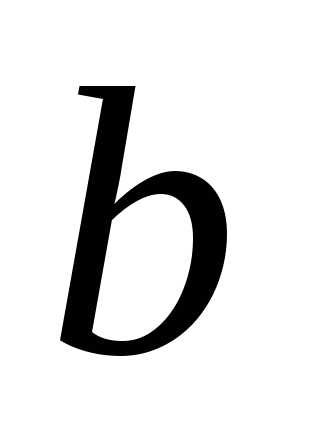 имеет кратность
имеет кратность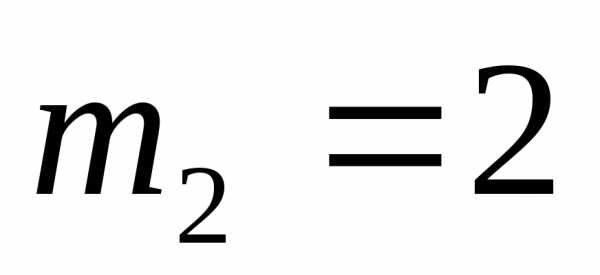 ,
элемент
,
элемент имеет кратность
имеет кратность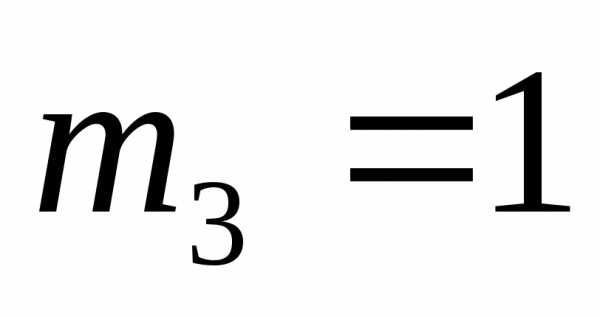 ,
элемент
,
элемент имеет кратность
имеет кратность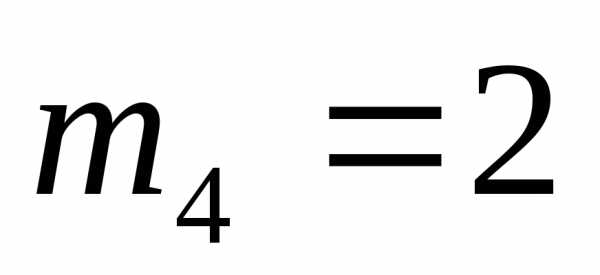 .
Сумма всех кратностей равна порядку
сочетания,
т.е..
Поставим каждому сочетанию в соответствие
последовательность из нулей и единиц,
составленную по такому правилу: напишем
подряд столько единиц, сколько элементов
первого типа в него входит, затем нуль,
затем напишем столько единиц, сколько
элементов второго типа в него входит,
затем нуль и т.д. Например, сочетанию с
повторениями
.
Сумма всех кратностей равна порядку
сочетания,
т.е..
Поставим каждому сочетанию в соответствие
последовательность из нулей и единиц,
составленную по такому правилу: напишем
подряд столько единиц, сколько элементов
первого типа в него входит, затем нуль,
затем напишем столько единиц, сколько
элементов второго типа в него входит,
затем нуль и т.д. Например, сочетанию с
повторениями соответствует последовательность
11101101011. Если некоторый элемент не
содержится в данном сочетании с
повторениями, т.е. его кратность равна
нулю, то тогда группа единиц не пишется
и в последовательности появится 0 по
меньшей мере два раза. В элементах
последовательности из нулей и единиц,
соответствующих сочетаниям с повторениями
из
соответствует последовательность
11101101011. Если некоторый элемент не
содержится в данном сочетании с
повторениями, т.е. его кратность равна
нулю, то тогда группа единиц не пишется
и в последовательности появится 0 по
меньшей мере два раза. В элементах
последовательности из нулей и единиц,
соответствующих сочетаниям с повторениями
из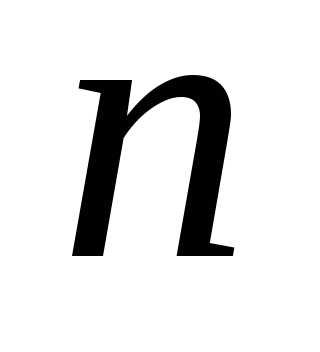 элементов по
элементов по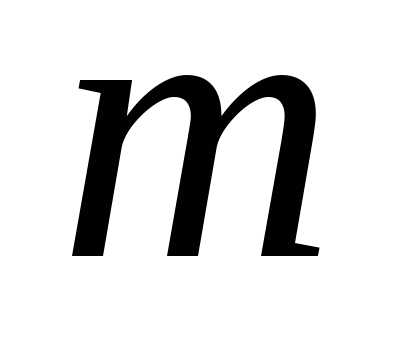 цифра 1 встречается
цифра 1 встречается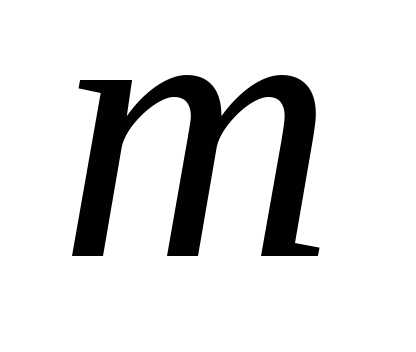 раз, а цифра 0 встречается
раз, а цифра 0 встречается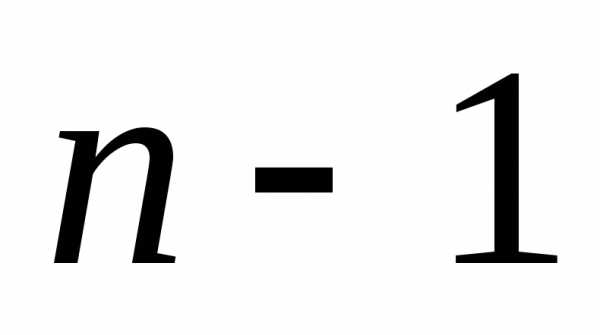 раз. Для сочетания
раз. Для сочетания соответственно 8 и 3. Всевозможные
сочетания с повторениями получатся,
если подвергнуть перестановке нули и
единицы в соответствующей последовательности.
соответственно 8 и 3. Всевозможные
сочетания с повторениями получатся,
если подвергнуть перестановке нули и
единицы в соответствующей последовательности.
Каждому
сочетанию с повторениями из 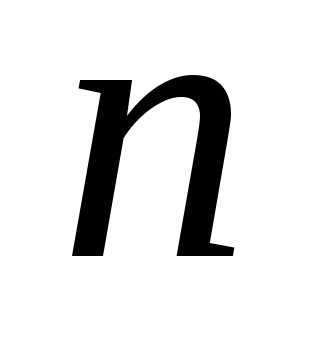 элементов по
элементов по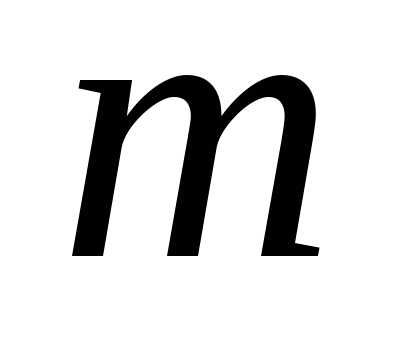 соответствует последовательность из
соответствует последовательность из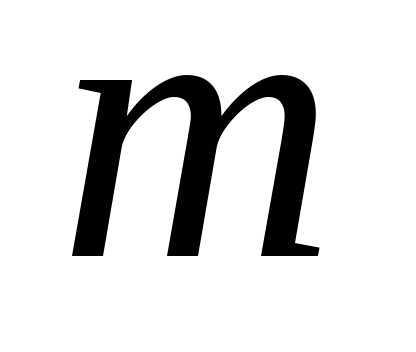 единиц и
единиц и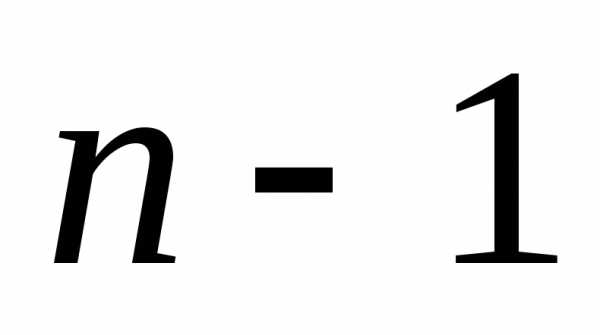 нулей. Следовательно, число сочетаний
с повторениями из
нулей. Следовательно, число сочетаний
с повторениями из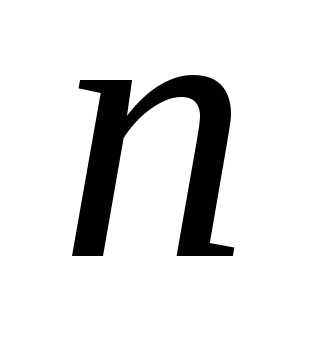 элементов по
элементов по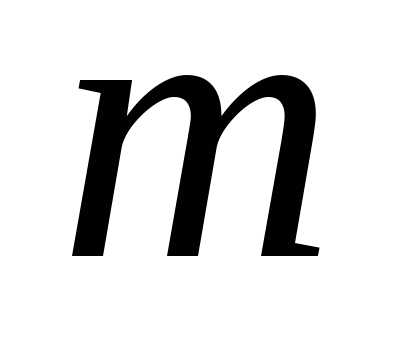 равно числу последовательностей из
равно числу последовательностей из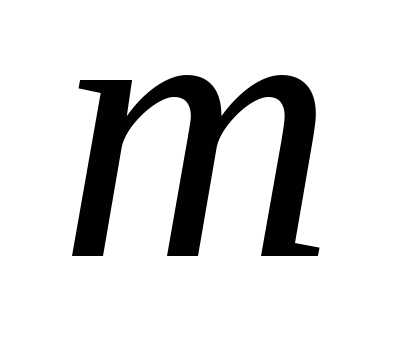 единиц и
единиц и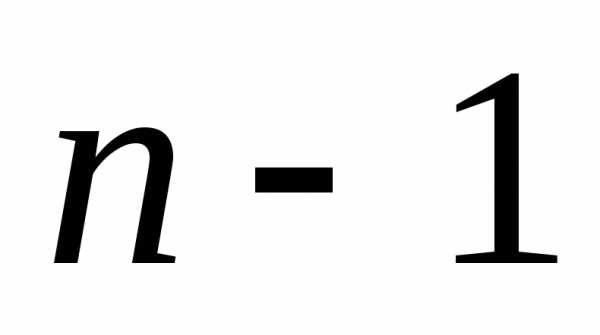 нулей. Это число определяется числом
перестановок с повторениями
нулей. Это число определяется числом
перестановок с повторениями
, т.е. .
Например,
сочетания из 4-х элементов 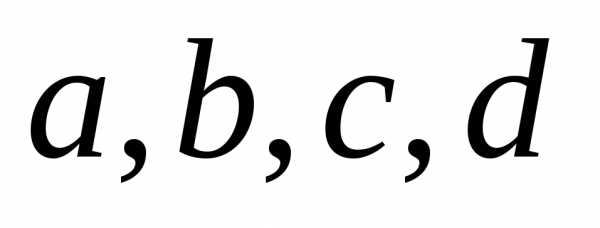 по 2 с повторениями будут.
Им соответствуют следующие последовательности
из нулей и единиц
по 2 с повторениями будут.
Им соответствуют следующие последовательности
из нулей и единиц
Пример 1.14.
В магазине 12 сортов пирожных. Покупатель хочет купить шесть пирожных, не обязательно разных. Сколько вариантов выбора у него есть?
Здесь производится выбор шести предметов из неограниченного количества предметов 12-ти различных сортов.
,
то есть шесть пирожных, не обязательно разных, можно выбрать 12376 способами.
studfiles.net
Сочетания.
1) Сочетания без повторений.
Определение
3: Сочетания
из 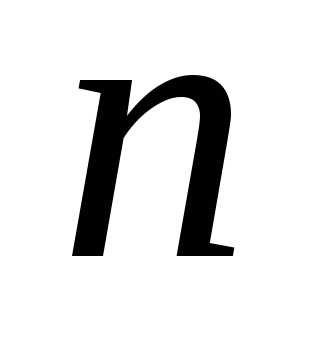 элементов по
элементов по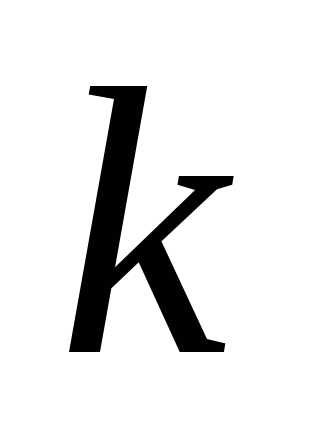 элементов (
элементов (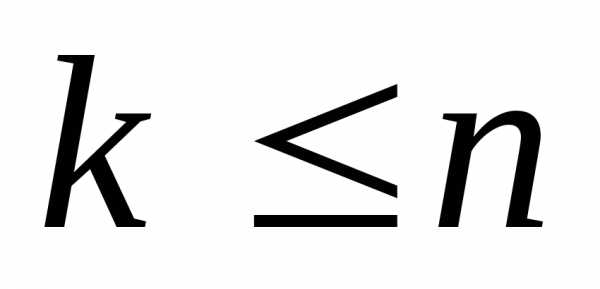 )
– это расстановки, отличающиеся друг
от другасоставом,
но не порядком элементов. Обозначают:
)
– это расстановки, отличающиеся друг
от другасоставом,
но не порядком элементов. Обозначают: 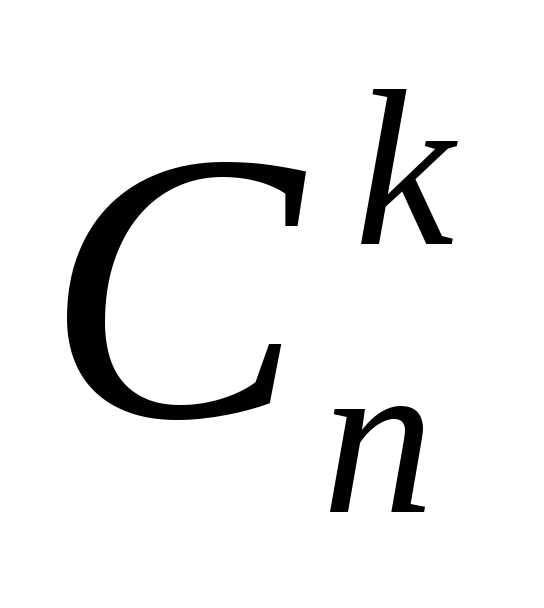 .
.
Теорема 4: Число сочетаний находится по следующей формуле:
.
Доказательство: 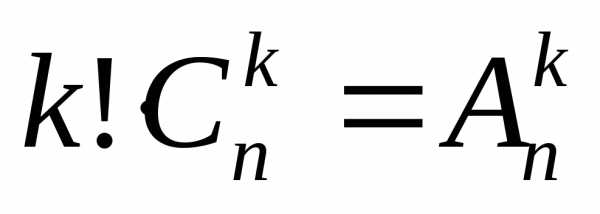 .
.
Следствие: Выведенная формула совпадает с формулой
для числа повторений из 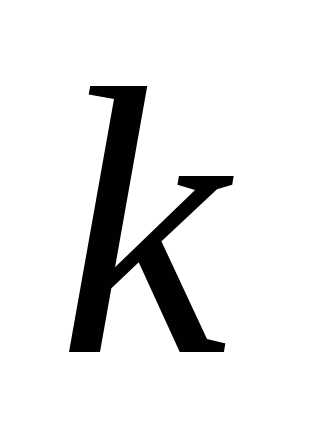 элементов одного типа и
элементов одного типа и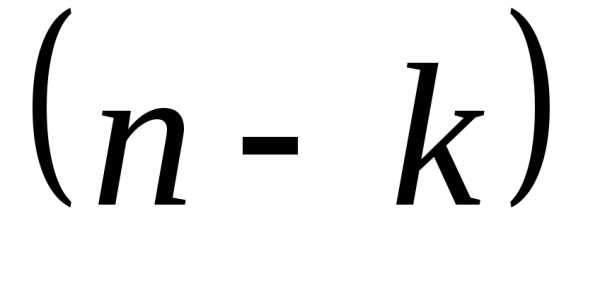 элементов второго типа:
элементов второго типа:
.
Иными словами справедливо равенство: .
Примеры: Выбор делегации, число призеров в соревновании и т. д.
Замечание: 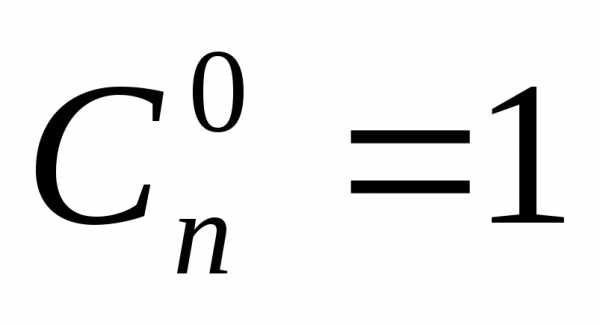 ,
, 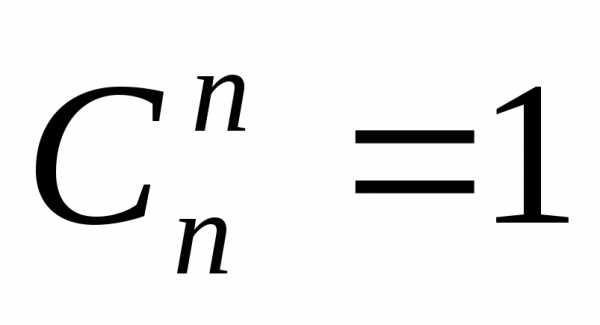 .
.
Существенное отличие числа сочетаний от числа соответствующих размещений состоит в том, что для размещений важен состав и порядок элементов в подмножествах, а для сочетаний важен только состав.
2) Сочетания с повторениями.
Пусть
имеется предметы 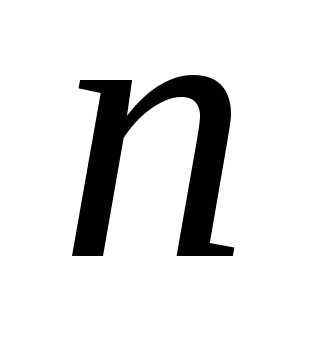 различных типов. Сколько
различных типов. Сколько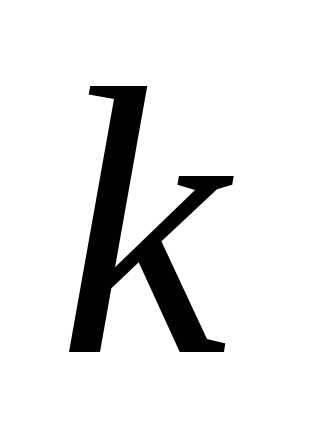 комбинаций можно сделать из них, если
не принимать во внимание порядок
элементов? Эту задачу в общем виде можно
решать точно так же, как задачу с
пирожными.
комбинаций можно сделать из них, если
не принимать во внимание порядок
элементов? Эту задачу в общем виде можно
решать точно так же, как задачу с
пирожными.
Задача: В кондитерском магазине продаются пирожные 4 сортов: наполеон, эклеры, песочные и слоеные. Сколькими способами можно купить 7 пирожных?
Зашифруем каждую покупку с помощью нулей и единиц. Напишем столько единиц, сколько куплено наполеонов, затем пишем 0, чтобы отделить пирожные одного типа от другого и т.д. Тогда каждой покупке будет соответствовать последовательность из семи единиц и трех нулей в различном порядке. Число всех таких покупок тогда будет равно:
.
Для числа сочетаний с повторениями существует формула:
.
§2. Свойства сочетаний. Бином Ньютона.
Одной из наиболее распространённых комбинаторных формул является формула числа сочетаний. Для упрощения подсчётов и для доказательства некоторых утверждений удобно использовать следующие свойства сочетаний:
1. 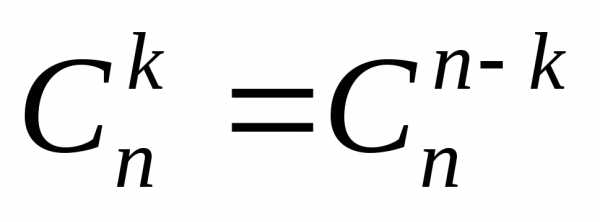 .
.
2. .
Доказательство:
1) .
2) .
Сочетания можно встретить и в школьном курсе математики. Например, в качестве коэффициентов бинома Ньютона выступают именно сочетания. Формула бинома Ньютона в общем виде и её доказательство приводятся в следующей теореме.
Теорема 1: .
Доказательство: Применим индукцию по 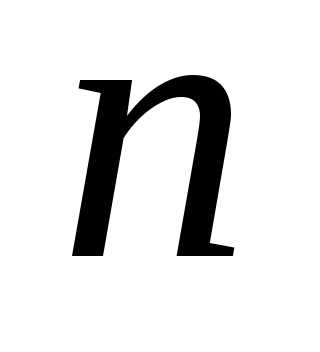 .
.
При 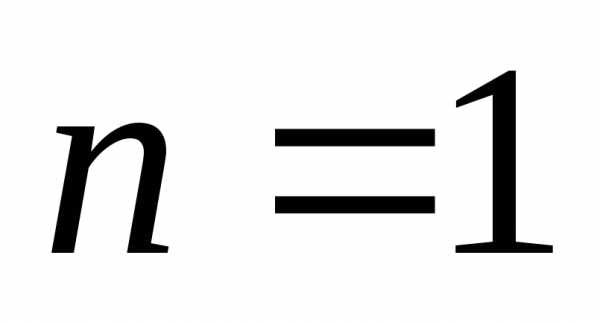 :.
:.
Пусть формула верна, для случая, когда . В этом случае следующее равенство будем считать выполненным:
.
Покажем,
что формула выполняется для 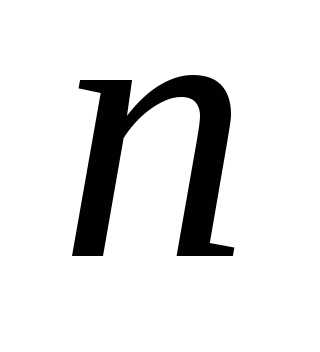 —
й степени:
—
й степени:
.
В доказательстве можно также использовать свойство: .
Следствие: Рассмотрим некоторые частные случаи формулы бинома Ньютона:
1) если , то.
2) если , то.
Определение
1: Коэффициенты 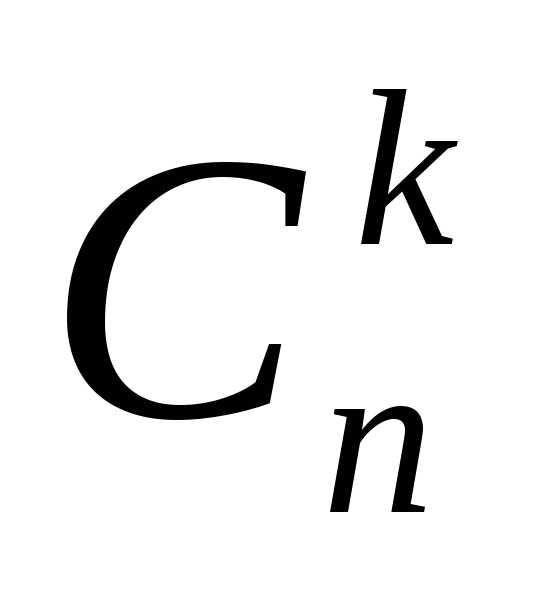 бинома Ньютонаназываются
биномиальными коэффициентами.
бинома Ньютонаназываются
биномиальными коэффициентами.
Числовые
значения биномиальных коэффициентов
вычисляются по формуле числа сочетаний: 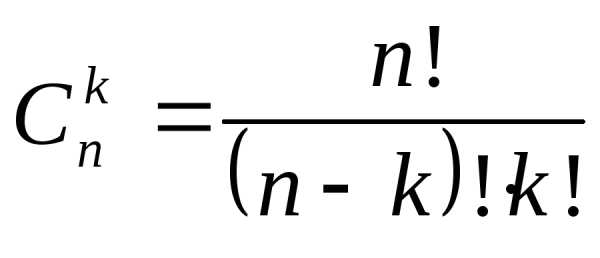 .
Готовые значения этих коэффициентов
располагаются в строкахтреугольника
Паскаля.
.
Готовые значения этих коэффициентов
располагаются в строкахтреугольника
Паскаля.
1 n = 0
1 1 n = 1
1 2 1 n = 2
1 3 3 1 n = 3
1 4 6 4 1 n = 4
1 5 10 10 5 1 n = 5
. . . . . . . . . . . . . . . . . . . . . . . . .
Треугольник
Паскаля строится следующим образом.
Боковые стороны состоят из единиц.
Числа, находящиеся внутри, являются
суммой вышестоящих чисел. Каждая строка
треугольника соответствует некоторой
степени для суммы 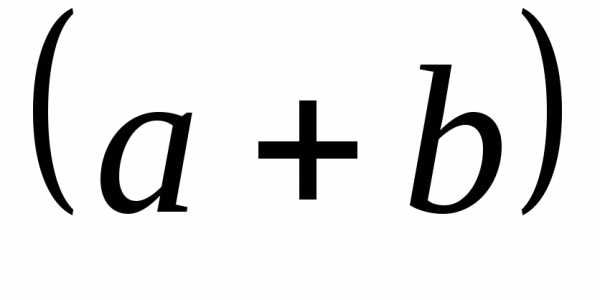 и содержит соответствующие биномиальные
коэффициенты. Таким образом, для того,
чтобы раскрыть степень суммы
и содержит соответствующие биномиальные
коэффициенты. Таким образом, для того,
чтобы раскрыть степень суммы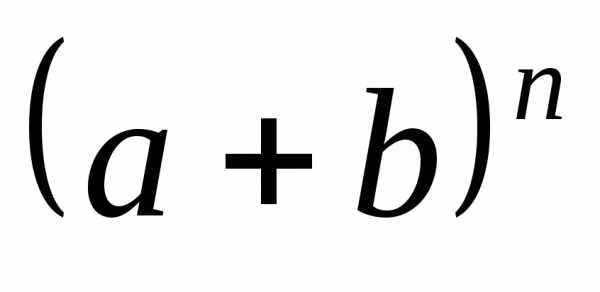 ,
нужно из треугольника Паскаля взять
строку, соответствующую данной степени
,
нужно из треугольника Паскаля взять
строку, соответствующую данной степени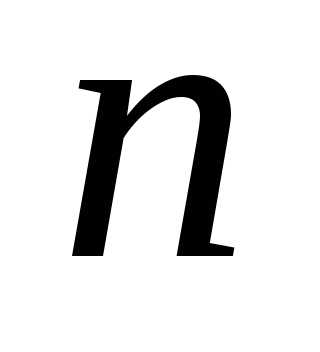 .
Эта строка будет содержать нужные
коэффициенты
.
Эта строка будет содержать нужные
коэффициенты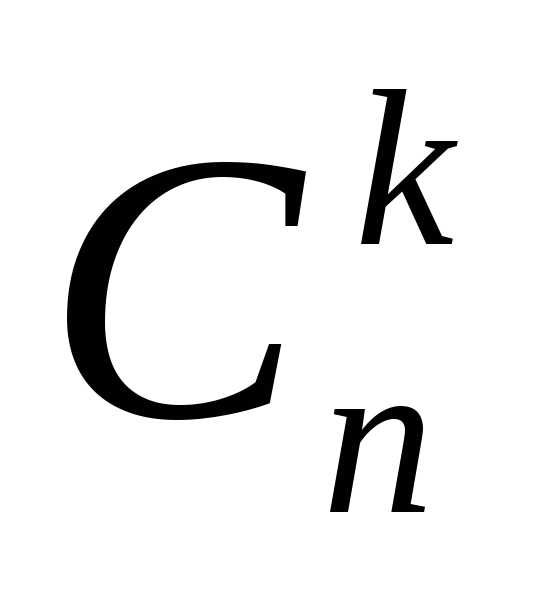 ,
к которым приписываются соответствующие
буквенные выражения. Можно заметить,
что строки треугольника Паскаля
симметричны, поэтому достаточно взять
только половину биномиальных коэффициентов
и, если нужно, средний элемент.
,
к которым приписываются соответствующие
буквенные выражения. Можно заметить,
что строки треугольника Паскаля
симметричны, поэтому достаточно взять
только половину биномиальных коэффициентов
и, если нужно, средний элемент.
Формула бинома Ньютона применяется, когда нужно возвести в целую степень сумму двух слагаемых. Если же это требуется произвести для суммы трёх и более слагаемых, тогда применяют полиномиальную формулу:
Сумма
в правой части формулы строится по
аналогии с формулой бинома. Она
представляет собой сумму слагаемых,
состоящих из коэффициента
и буквенной части.
Сумма этих слагаемых берется по
всевозможным разбиениям числа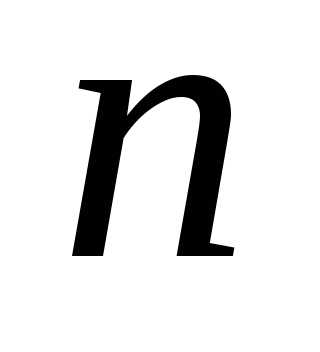 на
на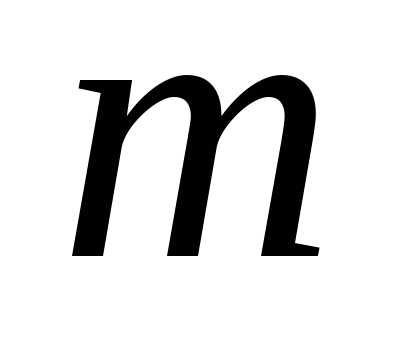 целых неотрицательных слагаемых,
при этом коэффициент находится по
формуле числа перестановок с повторениями:
целых неотрицательных слагаемых,
при этом коэффициент находится по
формуле числа перестановок с повторениями:
.
Если
числа 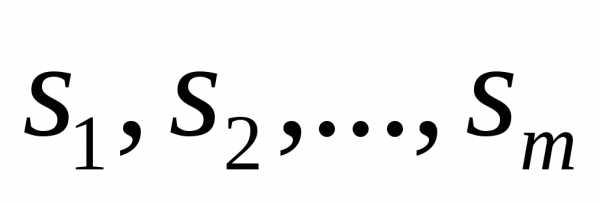 получаются перестановкой из чисел,
то считается, что
получаются перестановкой из чисел,
то считается, что
.
Пример: Возвести в пятую степень сумму трёх слагаемых.
Здесь учитывается, что 5 можно разбить на 3 слагаемых пятью способами:
;;;;.
Тогда
для каждого такого разбиения известны
числа 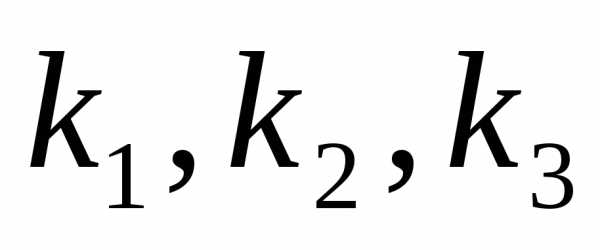 ,
,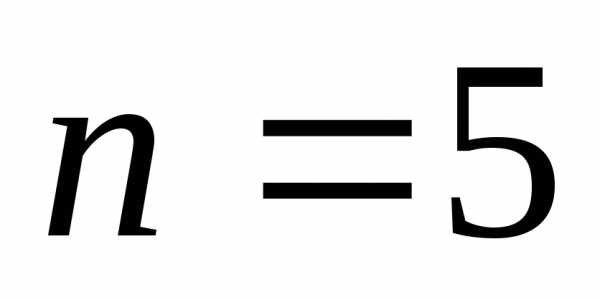 .
Значит, все коэффициенты можно для
каждого случая найти по формуле:
.
Значит, все коэффициенты можно для
каждого случая найти по формуле:
.
Полученные
коэффициенты: 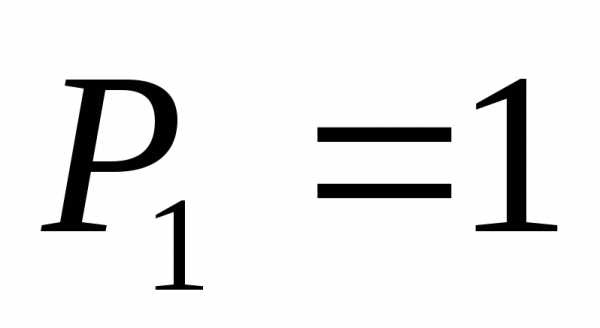 ,
,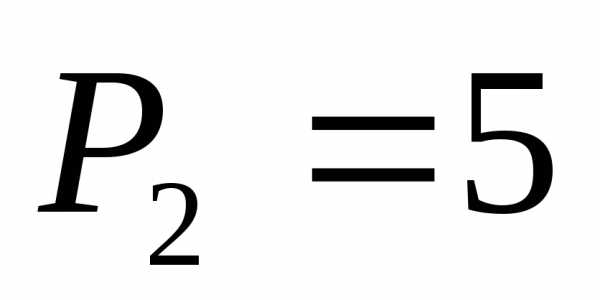 ,
,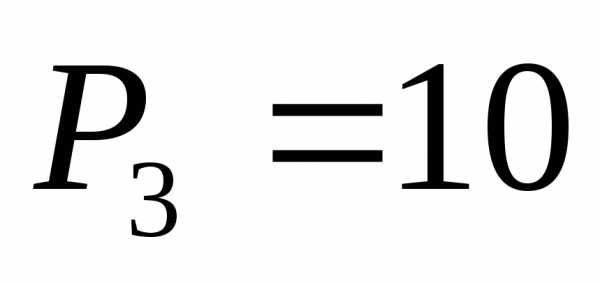 ,
,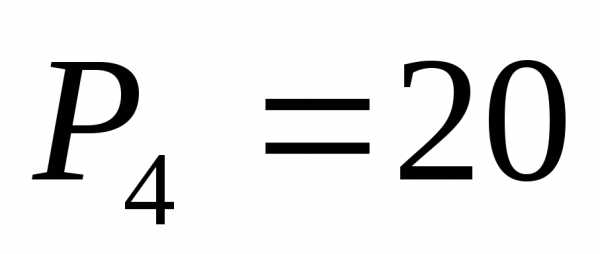 ,
,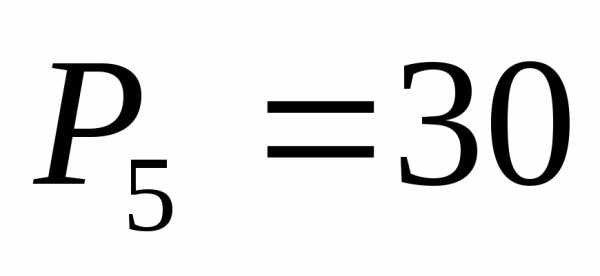 .
Буквенная часть также формируется в
связи с разложениями числа 5 на 3 слагаемых.
Таким образом, получается разложение,
приведённое выше.
.
Буквенная часть также формируется в
связи с разложениями числа 5 на 3 слагаемых.
Таким образом, получается разложение,
приведённое выше.
Замечание: Сумма полиномиальных коэффициентов может быть найдена по формуле:
.
Для коэффициентов из рассмотренного примера можно проверить:
,
.
Рассмотрим 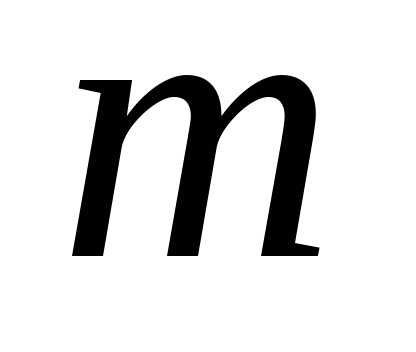 —
сочетания с повторениями, составленные
из элементов
—
сочетания с повторениями, составленные
из элементов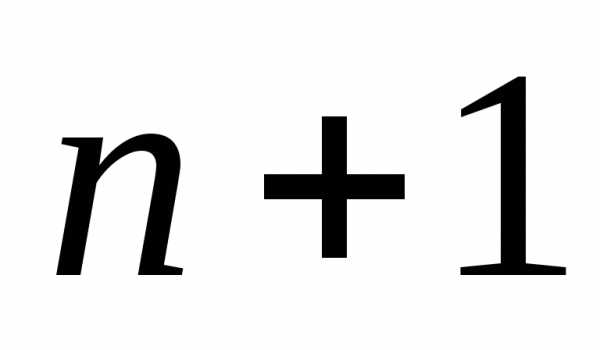 типа, например из
типа, например из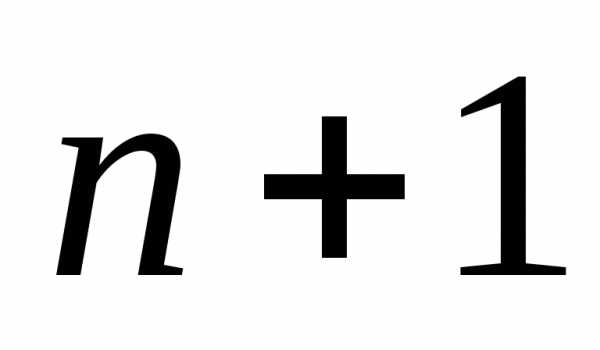 буквы.
Число таких сочетаний равно:
буквы.
Число таких сочетаний равно: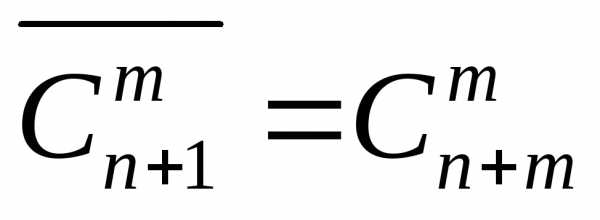 .
Разобьём все эти сочетания на классы,
отнеся к
.
Разобьём все эти сочетания на классы,
отнеся к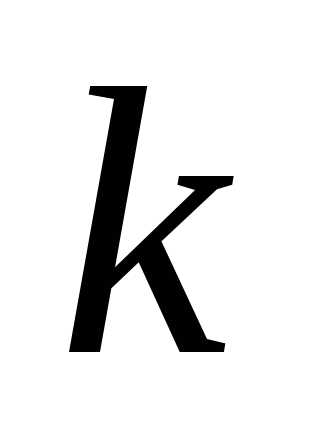 ‑
му классу сочетания, в которых
‑
му классу сочетания, в которых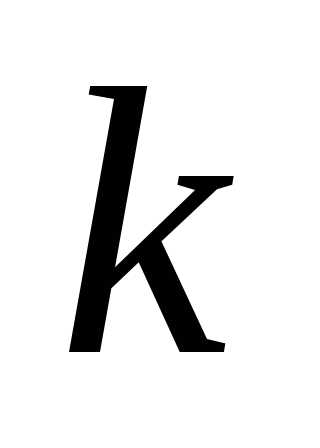 раз входит буква
раз входит буква .
Остальные
.
Остальные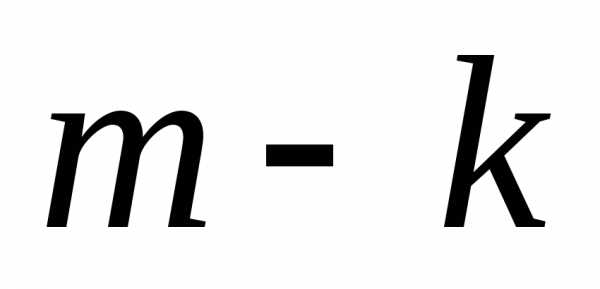 мест могут быть заняты оставшимися
буквами
мест могут быть заняты оставшимися
буквами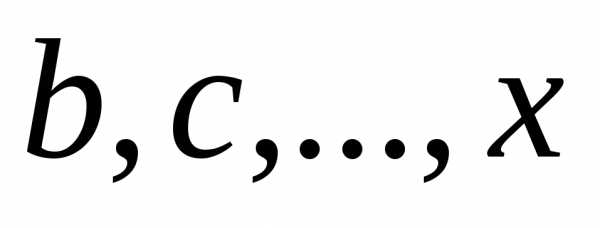 ,
число которых равно
,
число которых равно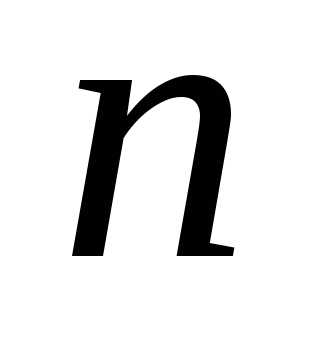 .
Поэтому в
.
Поэтому в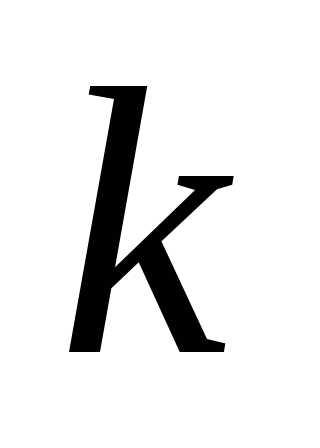 —
й класс входит столько сочетаний, сколько
можно составить
—
й класс входит столько сочетаний, сколько
можно составить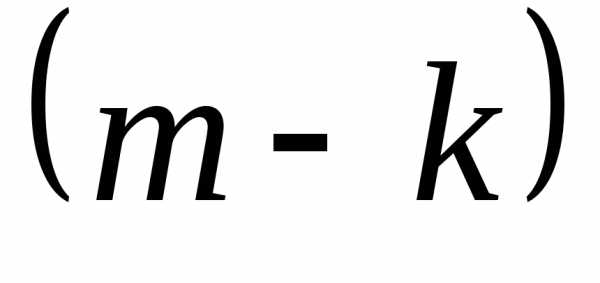 сочетаний с повторениями из элементов
сочетаний с повторениями из элементов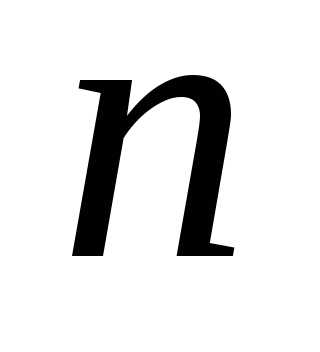 типов, т.е.
типов, т.е.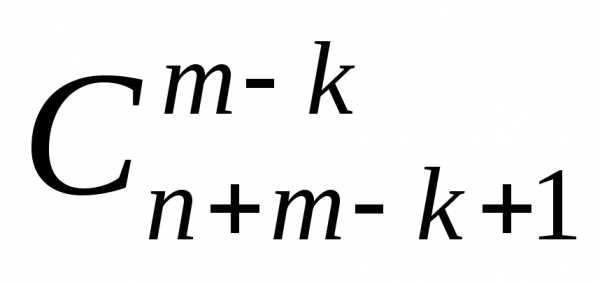 .
.
Значит общее число всех таких сочетаний равно:
, т.е.
.
Меняя
теперь 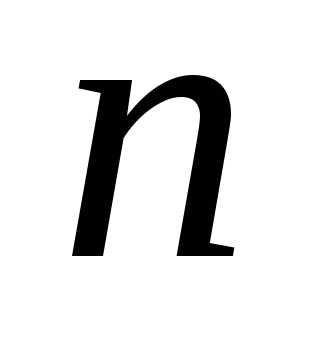 на
на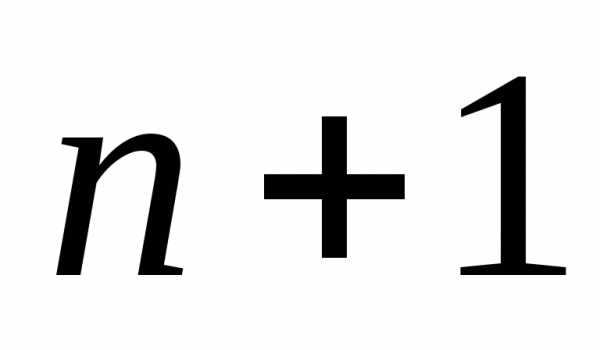 и
и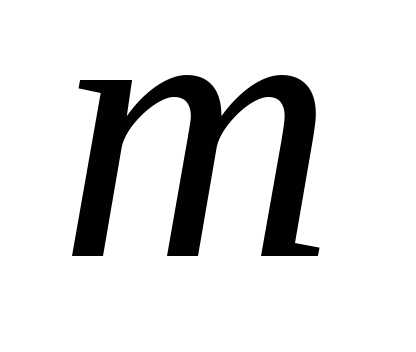 на
на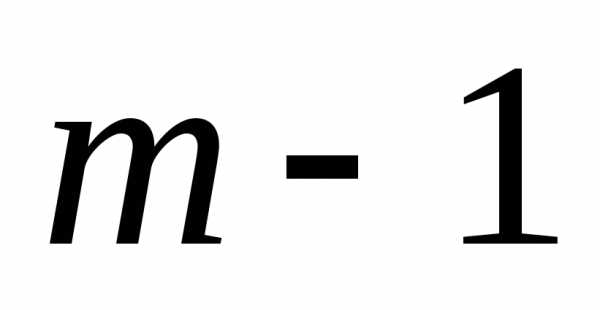 и используя равенство
и используя равенство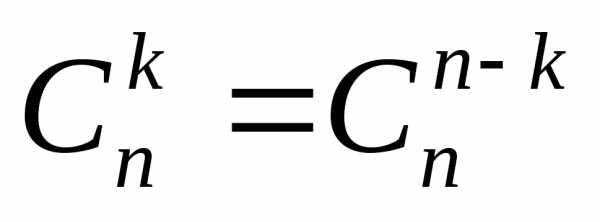 ,
получаем зависимость между биномиальными
коэффициентами:
,
получаем зависимость между биномиальными
коэффициентами:
.
Доказать
эту формулу можно методом математической
индукции по числу слагаемых в правой
части. Используя эту зависимость, можно
получить формулы для подсчёта суммы
чисел натурального ряда от 1 до 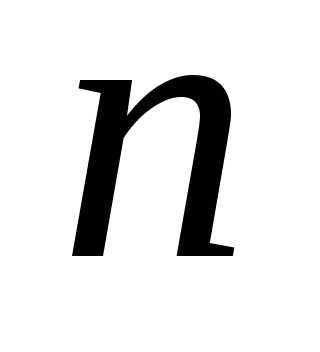 (при
(при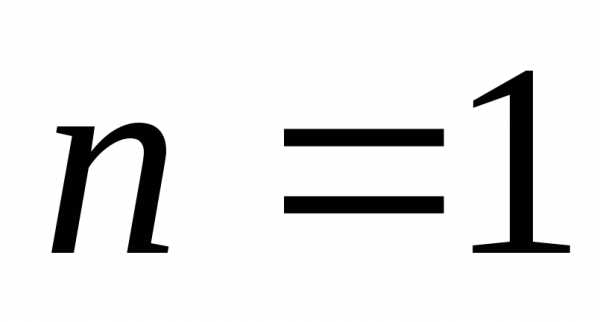 ),
суммы квадратов натуральных чисел (при
),
суммы квадратов натуральных чисел (при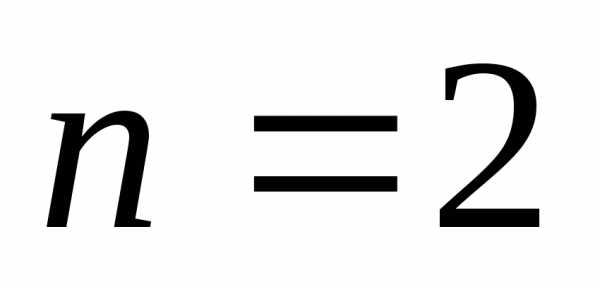 ),
сумму кубов (при
),
сумму кубов (при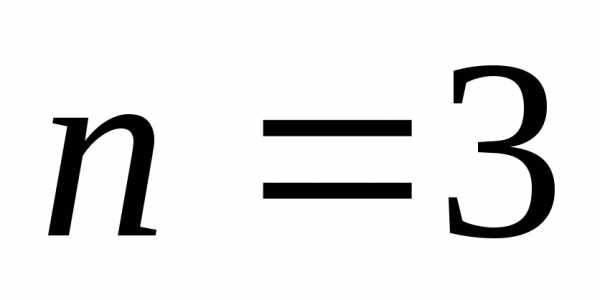 ).
).
Если 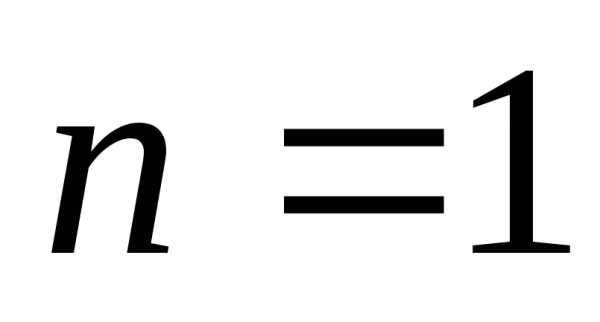 ,
то искомая зависимость имеет вид:
,
то искомая зависимость имеет вид:
.
Для 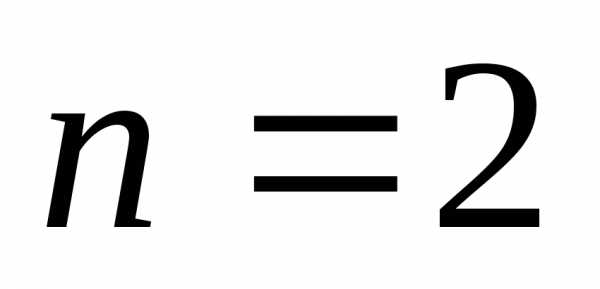 имеем:
имеем:
,
или окончательно:
.
Для 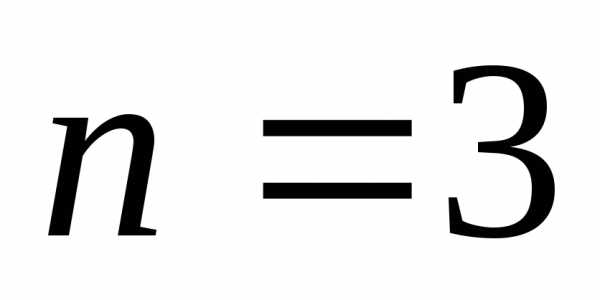 получаем:
получаем:
,
или после преобразований:
.
Таким образом, можно получить формулы для сумм более высоких степеней натуральных чисел.
studfiles.net
35 Элементы комбинаторики-перестановки,размещения, сочетания
В комбинаторике изучают вопросы о том, сколько комбинаций определенного типа можно составить из данных предметов (элементов).
Рождение комбинаторики как раздела математикисвязано с трудами Б. Паскаля и П. Ферма по теории азартных игр. Большой вклад в развитие комбинаторных методов внесли Г.В. Лейбниц, Я. Бернулли и Л. Эйлер.
Французский философ, писатель, математик и физик Блез Паскаль (1623–1662) рано проявил свои выдающиеся математические способности. Круг математических интересов Паскаля был весьма разнообразен. Паскаль доказал одну из основных теорем проективной геометрии (теорема Паскаля), сконструировал суммирующую машину (арифмометр Паскаля), дал способ вычисления биномиальных коэффициентов (треугольник Паскаля), впервые точно определил и применил для доказательства метод математической индукции, сделал существенный шаг в развитии анализа бесконечно малых, сыграл важную роль в зарождении теории вероятности. В гидростатике Паскаль установил ее основной закон (закон Паскаля). “Письма к провинциалу” Паскаля явились шедевром французской классической прозы.
Готфрид Вильгельм Лейбниц (1646–1716) — немецкий философ, математик, физик и изобретатель, юрист, историк, языковед. В математике наряду с И. Ньютоном разработал дифференциальное и интегральное исчисление. Важный вклад внес в комбинаторику. С его именем, в частности, связаны теоретико-числовые задачи.
Готфрид Вильгельм Лейбниц имел мало внушительную внешность и поэтому производил впечатление довольно невзрачного человека. Однажды в Париже он зашел в книжную лавку в надежде приобрести книгу своего знакомого философа. На вопрос посетителя об этой книге книготорговец, осмотрев его с головы до ног, насмешливо бросил: “Зачем она вам? Неужели вы способны читать такие книги?” Не успел ученый ответить, как в лавку вошел сам автор книги со словами: “Великому Лейбницу привет и уважение!” Продавец никак не мог взять втолк, что перед ним действительно знаменитый Лейбниц, книги которого пользовались большим спросом среди ученых.
В дальнейшем важную роль будет играть следующая
Лемма. Пусть в множестве элементов, а в множестве—элементов. Тогда число всех различных пар, гдебудет равно.
Доказательство. Действительно, с одним элементом из множества мы можем составитьтаких различных пар, а всего в множествеэлементов.
Размещения, перестановки, сочетания
Пусть у нас есть множество из трех элементов . Какими способами мы можем выбрать из этих элементов два?.
Определение. Размещениями множества из различных элементов поэлементовназываются комбинации, которые составлены из данныхэлементов поэлементов и отличаются либо самими элементами, либо порядком элементов.
Число всех размещений множества из элементов поэлементов обозначается через(от начальной буквы французского слова “arrangement”, что означает размещение), гдеи.
Теорема. Число размещений множества из элементов поэлементов равно
Доказательство. Пусть у нас есть элементы . Пусть— возможные размещения. Будем строить эти размещения последовательно. Сначала определим— первый элемент размещения. Из данной совокупностиэлементов его можно выбратьразличными способами. После выбора первого элементадля второго элементаостаетсяспособов выбора и т.д. Так как каждый такой выбор дает новое размещение, то все эти выборы можно свободно комбинировать между собой. Поэтому имеем:
Пример. Сколькими способами можно составить флаг, состоящий из трех горизонтальных полос различных цветов, если имеется материал пяти цветов?
Решение. Искомое число трехполосных флагов:
Определение. Перестановкой множества из элементов называется расположение элементов в определенном порядке.
Так, все различные перестановки множества из трех элементов — это
Очевидно, перестановки можно считать частным случаем размещений при .
Число всех перестановок из элементов обозначается(от начальной буквы французского слова “permutation”, что значит “перестановка”, “перемещение”). Следовательно, число всех различных перестановок вычисляется по формуле
Пример. Сколькими способами можно расставить 8 ладей на шахматной доске так, чтобы они не били друг друга?
Решение. Искомое число расстановки 8 ладей
по определению!
Определение. Сочетаниями из различных элементов поэлементов называются комбинации, которые составлены из данныхэлементов поэлементов и отличаются хотя бы одним элементом (иначе говоря,-элементные подмножества данного множества изэлементов).
Как видим, в сочетаниях в отличие от размещений не учитывается порядок элементов. Число всех сочетаний из элементов поэлементов в каждом обозначается(от начальной буквы французского слова “combinasion”, что значит “сочетание”).
Числа
Все сочетания из множества по два —.
.
studfiles.net
Сочетание — Википедия
Материал из Википедии — свободной энциклопедии
В комбинаторике сочетанием из n{\displaystyle n} по k{\displaystyle k} называется набор k{\displaystyle k} элементов, выбранных из данного множества, содержащего n{\displaystyle n} различных элементов.
Наборы, отличающиеся только порядком следования элементов (но не составом), считаются одинаковыми, этим сочетания отличаются от размещений.
Так, например, наборы (3-элементные сочетания, подмножества, k=3{\displaystyle k=3}) {2, 1, 3} и {3, 2, 1} 6-элементного множества {1, 2, 3, 4, 5, 6} (n=6{\displaystyle n=6}) являются одинаковыми (в то время как размещения были бы разными) и состоят из одних и тех же элементов {1,2,3}.
В общем случае число, показывающее, сколькими способами можно выбрать k{\displaystyle k} элементов из множества, содержащего n{\displaystyle n} различных элементов, стоит на пересечении k{\displaystyle k}
ru.wikipedia.org
Основные формулы комбинаторики. Комбинаторика: формула перестановки, размещения
В данной статье речь пойдет об особом разделе математики под названием комбинаторика. Формулы, правила, примеры решения задач – все это вы сможете найти здесь, прочитав статью до самого конца.
Итак, что же это за раздел? Комбинаторика занимается вопросом подсчета каких-либо объектов. Но в данном случае объектами выступают не сливы, груши или яблоки, а нечто иное. Комбинаторика помогает нам находить вероятность какого-либо события. Например, при игре в карты – какова вероятность того, что у противника есть козырная карта? Или такой пример – какова вероятность того, что из мешка с двадцатью шариками вы достанете именно белый? Именно для подобного рода задач нам и нужно знать хотя бы основы данного раздела математики.
Комбинаторные конфигурации
Рассматривая вопрос основных понятий и формул комбинаторики, мы не можем не уделить внимание комбинаторным конфигурациям. Они используются не только для формулировки, но и для решения различных комбинаторных задач. Примерами таких моделей служат:
- размещение;
- перестановка;
- сочетание;
- композиция числа;
- разбиение числа.
О первых трех мы поговорим более подробно далее, а вот композиции и разбиению мы уделим внимание в данном разделе. Когда говорят о композиции некого числа (допустим, а), то подразумевают представление числа а в виде упорядоченной суммы неких положительных чисел. А разбиение – это неупорядоченная сумма.
Разделы

Прежде чем мы перейдем непосредственно к формулам комбинаторики и рассмотрению задач, стоит обратить внимание на то, что комбинаторика, как и другие разделы математики, имеет свои подразделы. К ним относятся:
- перечислительная;
- структурная;
- экстремальная;
- теория Рамсея;
- вероятностная;
- топологическая;
- инфинитарная.
В первом случае речь идет об исчисляющей комбинаторике, задачи рассматривают перечисление или подсчет разных конфигураций, которые образованы элементами множеств. На данные множества, как правило, накладываются какие-либо ограничения (различимость, неразличимость, возможность повтора и так далее). А количество этих конфигураций подсчитывается при помощи правила сложения или умножения, о которых мы поговорим немного позже. К структурной комбинаторике относятся теории графов и матроидов. Пример задачи экстремальной комбинаторики – какова наибольшая размерность графа, который удовлетворяет следующим свойствам… В четвертом пункте мы упомянули теорию Рамсея, которая изучает в случайных конфигурациях наличие регулярных структур. Вероятностная комбинаторика способна нам ответить на вопрос – какова вероятность того, что у заданного множества присутствует определенное свойство. Как нетрудно догадаться, топологическая комбинаторика применяет методы в топологии. И, наконец, седьмой пункт – инфинитарная комбинаторика изучает применение методов комбинаторики к бесконечным множествам.
Правило сложения
Среди формул комбинаторики можно найти и довольно простые, с которыми мы достаточно давно знакомы. Примером является правило суммы. Предположим, что нам даны два действия (С и Е), если они взаимоисключаемы, действие С выполнимо несколькими способами (например а), а действие Е выполнимо b-способами, то выполнить любое из них (С или Е) можно а+b способами.

В теории это понять достаточно трудно, постараемся донести всю суть на простом примере. Возьмем среднюю численность учеников одного класса — допустим, это двадцать пять. Среди них пятнадцать девочек и десять мальчиков. Ежедневно в классе назначается один дежурный. Сколько есть способов назначить дежурного по классу сегодня? Решение задачи достаточно простое, мы прибегнем к правилу сложения. В тексте задачи не сказано, что дежурными могут быть только мальчики или только девочки. Следовательно, им может оказаться любая из пятнадцати девочек или любой из десяти мальчиков. Применяя правило суммы, мы получаем достаточно простой пример, с которым без труда справится школьник начальных классов: 15 + 10. Подсчитав, получаем ответ: двадцать пять. То есть существует всего двадцать пять способов назначить на сегодня дежурного класса.
Правило умножения
К основным формулам комбинаторики относится и правило умножения. Начнем с теории. Допустим, нам необходимо выполнить несколько действий (а): первое действие выполняется с1 способами, второе – с2 способами, третье – с3 способами и так далее до последнего а-действия, выполняемого са способами. Тогда все эти действия (которых всего у нас а) могут быть выполнены N способами. Как высчитать неизвестную N? В этом нам поможет формула: N = с1 * с2 * с3 *…* са.

Опять же, в теории ничего не понятно, переходим к рассмотрению простого примера на применение правила умножения. Возьмем все тот же класс из двадцати пяти человек, в котором учится пятнадцать девочек и десять мальчиков. Только на этот раз нам необходимо выбрать двух дежурных. Ими могут быть как только мальчики или девочки, так и мальчик с девочкой. Переходим к элементарному решению задачи. Выбираем первого дежурного, как мы решили в прошлом пункте, у нас получается двадцать пять возможных вариантов. Вторым дежурным может быть любой из оставшихся человек. У нас было двадцать пять учеников, одного мы выбрали, значит вторым дежурным может быть любой из оставшихся двадцати четырех человек. Наконец, применяем правило умножения и получаем, что двоих дежурных можно избрать шестью сотнями способов. Мы данное число получили умножением двадцати пяти и двадцати четырех.
Перестановка
Сейчас мы рассмотрим еще одну формулу комбинаторики. В данном разделе статьи мы поговорим о перестановках. Рассмотреть проблему предлагаем сразу же на примере. Возьмем бильярдные шары у нас их n-ое количество. Нам нужно подсчитать: сколько есть вариантов расставить их в ряд, то есть составить упорядоченный набор.
Начнем, если у нас нет шаров, то и вариантов расстановки у нас так же ноль. А если у нас шар один, то и расстановка тоже одна (математически это можно записать следующим образом: Р1 = 1). Два шара можно расставить двумя разными способами: 1,2 и 2,1. Следовательно, Р2 = 2. Три шара можно расставить уже шестью способами (Р3=6): 1,2,3; 1,3,2; 2,1,3; 2,3,1; 3,2,1; 3,1,2. А если таких шаров не три, а десять или пятнадцать? Перечислять все возможные варианты очень долго, тогда нам на помощь приходит комбинаторика. Формула перестановки поможет нам найти ответ на интересующий нас вопрос. Pn = n *P (n-1). Если попытаться упростить формулу, то получаем: Pn = n* (n — 1) *…* 2 * 1. А это и есть произведение первых натуральных чисел. Такое число называется факториалом, а обозначается как n!

Рассмотрим задачу. Вожатый каждое утро выстраивает свой отряд в шеренгу (двадцать человек). В отряде есть три лучших друга – Костя, Саша и Леша. Какова вероятность того, что они будут стоять рядом? Чтобы найти ответ на вопрос, нужно вероятность «хорошего» исхода поделить на общее количество исходов. Общее число перестановок составляет 20! = 2,5 квинтиллиона. Как посчитать количество «хороших» исходов? Предположим, что Костя, Саши и Леша – это один сверхчеловек. Тогда мы имеем всего восемнадцать субъектов. Число перестановок в данном случае равняется 18 = 6,5 квадриллионов. При всем этом, Костя, Саша и Леша могут произвольно перемещаться между собой в своей неделимой тройке, а это еще 3! = 6 вариантов. Значит всего «хороших» расстановок у нас 18! * 3! Нам остается только найти искомую вероятность: (18! * 3!) / 20! Что равняется примерно 0,016. Если перевести в проценты, то это получается всего 1,6%.
Размещение
Сейчас мы рассмотрим еще одну очень важную и необходимую формулу комбинаторики. Размещение – это наш следующий вопрос, который предлагаем вам рассмотреть в данном разделе статьи. Мы идем на усложнение. Предположим, что мы хотим рассмотреть возможные перестановки, только не из всего множества (n), а из меньшего (m). То есть мы рассматриваем перестановки из n предметов по m.
Основные формулы комбинаторики стоит не просто заучивать, а понимать их. Даже несмотря на то, что они усложняются, так как у нас не один параметр, а два. Предположим, что m = 1, то и А = 1, m = 2, то А = n * (n — 1). Если далее упрощать формулу и перейти на запись при помощи факториалов, то получится вполне лаконичная формула: А = n! / (n — m)!
Сочетание
Мы рассмотрели практически все основные формулы комбинаторики с примерами. Теперь перейдем к заключительному этапу рассмотрения базового курса комбинаторики – знакомство с сочетанием. Сейчас мы будем выбирать m предметов из имеющихся у нас n, при этом всем мы будем выбирать всеми возможными способами. Чем же тогда это отличается от размещения? Мы не будем учитывать порядок. Этот неупорядоченный набор и будет являться сочетанием.

Сразу введем обозначение: С. Берем размещения m шариков из n. Мы перестаем обращать внимание на порядок и получаем повторяющиеся сочетания. Чтобы получить число сочетаний нам надо поделить число размещений на m! (m факториал). То есть С = А / m! Таким образом, способов выбрать из n шаров немножко, равняется примерно столько, сколько выбрать почти все. Этому есть логическое выражение: выбрать немножко все равно, что выкинуть почти все. Еще в данном пункте важно упомянуть и то, что максимальное число сочетаний можно достигнуть при попытке выбрать половину предметов.
Как выбрать формулу для решения задачи?
Мы подробно рассмотрели основные формулы комбинаторики: размещение, перестановка и сочетание. Теперь наша задача – облегчить выбор необходимой формулы для решения задачи по комбинаторике. Можно воспользоваться следующей довольно простой схемой:
- Задайте себе вопрос: порядок размещения элементов учитывается в тексте задачи?
- Если ответ нет, то воспользуйтесь формулой сочетания (С = n! / (m! * (n — m)!)).
- Если ответ нет, то необходимо ответить на еще один вопрос: все ли элементы входят в комбинацию?
- Если ответ да, то воспользуйтесь формулой перестановки (Р = n!).
- Если ответ нет, то воспользуйтесь формулой размещения (А = n! / (n — m)!).
Пример
Мы рассмотрели элементы комбинаторики, формулы и некоторые другие вопросы. Теперь перейдем к рассмотрению реальной задачи. Представьте, что перед вами лежат киви, апельсин и банан.

Вопрос первый: сколькими способами их можно переставить? Для этого воспользуемся формулой перестановок: Р = 3! = 6 способов.
Вопрос второй: сколькими способами можно выбрать один фрукт? Это очевидно, у нас всего три варианта – выбрать киви, апельсин или банан, но применим формулу сочетаний: С = 3! / (2! * 1!) = 3.
Вопрос третий: сколькими способами можно выбрать два фрукта? Какие есть у нас вообще варианты? Киви и апельсин; киви и банан; апельсин и банан. То есть три варианта, но это легко проверить при помощи формулы сочетания: С = 3! / (1! * 2!) = 3
Вопрос четвертый: сколькими способами можно выбрать три фрукта? Как видно, выбрать три фрукта можно одним-единственным способом: взять киви, апельсин и банан. С = 3! / (0! * 3!) = 1.
Вопрос пятый: сколькими способами можно выбрать хотя бы один фрукт? Это условие подразумевает, что мы можем взять один, два или все три фрукта. Следовательно, мы складываем С1 + С2 + С3 =3 + 3 + 1 = 7. То есть у нас есть семь способов взять со стола хотя бы один фрукт.
fb.ru
