Портрет из треугольников или низкополигональный рисунок
Решила я разнообразить свои аватарки в ВК и добавить новое фото, что-нибудь нарисовав. Думала-думала и пришли на ум полигоны.
В сети гуляет множество рисунков с треугольниками: цветные и чёрно-белые, несложные и замысловатые, есть даже потрясающие эскизы низкополигональных татуировок. Но как же сделать подобное фото, и в какой программе?
Для меня проще всего это было сделать во флэше. Открываем программу Macromedia Flash Professional. Создаём новый документ, кидаем в него нужное фото.
Лучше выбрать фотографию с минимумом деталей и цветов, ведь множество мелочей на фото вы устанетесь превращать в треугольники, да и изображение в итоге должно быть легкоугадываемое, а не «рябь на картинке», по которой невозможно узнать, кто или что там на рисунке.
Я масштабирую на 400% изображение, и оно становится размытым. Не беда, ведь треугольники мы нарисуем в векторе. Готовую иллюстрацию можно будет уменьшать и увеличивать как угодно, она не потеряет качества.
Теперь создадим новый слой (сверху слева на фото, где написано Layer 1, и на новом слое начнем инструментом Line Tool (N) рисовать треугольники, соединяя их друг с другом.
Затем нужно их залить заливкой Paint Bucket Tool (K), взяв пипеткой преобладающий в данном треугольнике цвет прямо с изображения (фото).
Получается примерно так:
Когда вы обрисуете нужную вам часть, треугольники нарисованные инструментом Line Tool, можно удалить все разом, фото тоже следует удалить. Останутся лишь полигоны:
Такое готовое низкополигональное изображение можно трансформировать как угодно — бесконечно увеличивать или уменьшать, качества оно не потеряет.
Также есть способ сделать подобную картинку в Фотошопе. Подробно вы можете изучить кучу видео по теме размещённых на youtube, благо их там тьма.
Но кратенько я расскажу. Открываем Фотошоп, оздаем новый документ, на него новым слоем добавляем нужное вам фото. Можете сделать копию слоя с фото на всякий случай, но я прямо по фото начинаю рисовать полигоны — треугольники.
На видео советуют сделать сетку и много чего еще, но проще всего рисовать магнитным лассо прямо по фото. Выбираем какую-то деталь на фото и начинаем рисовать треугольники, примерно ориентируясь на форму или цвет изображения:
Рисуем магнитным лассо 2 стороны треугольника и кликаем 2 раза, третья сторона автоматически добавляется сама.
Теперь заливаем тругольник цветом, который является усреднённым в этом полигоне: Filter-Blur-Average. В следующий раз — просто команда ctrl+F повторит этот фильтр.
Рисуем несколько таких треугольников, сразу же заливая их средним цветом. Вот, что получается:
Обведя так нужное пространство, остальное — ненужное, обводим магнитным лассо и заливаем белой заливкой (как вариант).
Вот и всё!
Урок 28. треугольники — Математика — 5 класс
Математика
5 класс
Урок №28
Треугольники
Перечень рассматриваемых вопросов:
— треугольники;
— элементы треугольника;
— виды треугольников.
Тезаурус
Треугольник – это геометрическая фигура, состоящая из трёх точек, не лежащих на одной прямой и соединённых между собой.
Периметр треугольника – сумма длин всех сторон треугольника.
Обязательная литература
Никольский С. М. Математика. 5 класс. Учебник для общеобразовательных учреждений. // С. М. Никольский, М. К. Потапов, Н. Н. Решетников и др. – М.: Просвещение, 2017. – 272 с.
Дополнительная литература
1. Чулков П. В. Математика: тематические тесты. 5 класс. // П. В. Чулков, Е. Ф. Шершнёв, О. Ф. Зарапина. – М.: Просвещение, 2009. – 142 с.
2. Шарыгин И. Ф. Задачи на смекалку: 5-6 классы. // И. Ф. Шарыгин, А. В. Шевкин. – М.: Просвещение, 2014. – 95 с.
Теоретический материал для самостоятельного изучения
Среди всех многоугольников наименьшее число сторон и углов имеет треугольник. Он является простейшей фигурой, и казалось бы, его изучение не может быть интересным. Однако существует множество видов треугольников.
О них мы и поговорим.
Отметим какие-нибудь три точки, не лежащие на одной прямой – например, А, В, С. Соединим их с помощью линейки. Получим геометрическую фигуру, которая называется треугольником. Отмеченные три точки А, В, С называются вершинами, отрезки АВ, ВС, АС – сторонами треугольника, а углы А, В, С – углами треугольника.
Все треугольники можно разделить на группы по сторонам:
— если равных сторон нет – это разносторонний треугольник;
— если две стороны равны – это равнобедренный треугольник;
— если все стороны равны – это равносторонний треугольник.
Треугольники можно разделить на группы в зависимости от углов:
— если есть тупой угол – это тупоугольный треугольник;
— если все углы острые – это остроугольный треугольник;
— если есть прямой угол – это прямоугольный треугольник.
Треугольники, соединяясь друг с другом, могут образовывать другие фигуры.
Попробуем нарисовать прямоугольный треугольник на листе в клетку.
По сторонам клетки проведём отрезки заданной длины из одной точки. В нашем случае из точки А проведём отрезки длиной четыре и три сантиметра, что соответствует восьми и шести клеткам. На концах отрезков поставим точки В и С и соединим их между собой. Таким образом, мы построили прямоугольный треугольник АВС.
А теперь рассмотрим свойства треугольников. Одно из них – жёсткость. Это свойство заключается в том, что, если взять три рейки и соединить их попарно, то получится треугольник, изменить форму которого можно лишь сломав рейку.
Рассмотрим ещё одно свойство треугольников. Оно заключается в том, что длина каждой стороны треугольника всегда меньше суммы двух других сторон.
Это свойство можно использовать для проверки возможности построения треугольника по определённым сторонам. То есть, если свойство не выполняется, то такого треугольника не может быть.
Если мы знаем стороны треугольника, то можем найти его периметр как сумму длин всех его сторон. Например, периметр треугольника АВС – это сумма сторон АВ, АС и ВС.
Р = АВ + ВС + АС
Измерим с помощью линейки стороны треугольника и рассчитаем его периметр.
По результатам измерения стороны, соответственно, равны пяти, шести и семи сантиметрам.
Значит, периметр равен восемнадцати сантиметрам, то есть сумме всех сторон.
Говоря о треугольниках, стоит упомянуть, что они бывают как одинаковыми, так и разными. Определить, равные или разные треугольники, можно способом наложения. Если треугольник полностью накладывается на другой треугольник, такие треугольники равны. В противном случае треугольники не будут равными.
Рисунки из треугольников
Многие люди, как маленькие, так и взрослые, очень любят рисовать. Но иногда одного желания рисовать недостаточно. Для того чтобы облегчить процесс создания простейших картинок, инженер Эриф Мд. Вейлиула Байан, разработчик инновационного контента для детей, создал схемы, по которым, имея базовые навыки работы с чертёжными инструментами, можно создать милые и забавные картинки с животными и птицами.
Похожие схемы частично есть в открытом доступе, поэтому каждый желающий может приобщиться к миру изобразительного искусства через поэтапное прорисовывание простых картинок.
Тренировочные задания
№ 1. В треугольнике все стороны равны 15 см. Чему равен периметр треугольника?
Решение: для нахождения периметра используем формулу Р = АВ + АС + ВС.
Так как у этого треугольника стороны равны, то Р = 15 см + 15 см + 15 см = 45 см
№ 2. Сопоставьте треугольники с их видами (по углам).
Решение: в задаче требуется сопоставить треугольники со следующими видами по углам: остроугольный, прямоугольный, тупоугольный. Согласно определению, прямоугольный треугольник имеет один угол 90 градусов: этому треугольнику соответствует второй треугольник. А тупоугольный треугольник имеет один угол больше 90 градусов: он отображён третьим по счёту. Как мы знаем, остроугольный треугольник имеет три угла меньше 90 градусов, так что в этом случае подходит треугольник, изображённый первым слева.
%d1%82%d1%80%d0%b5%d1%83%d0%b3%d0%be%d0%bb%d1%8c%d0%bd%d0%b8%d0%ba PNG, векторы, PSD и пнг для бесплатной загрузки
Мемфис дизайн геометрические фигуры узоры мода 80 90 х годов
4167*4167
поп арт 80 х патч стикер
3508*2480
естественный цвет bb крем цвета
1200*1200
аудиокассета изолированные вектор старая музыка ретро плеер ретро музыка аудиокассета 80 х пустой микс
5000*5000
поп арт 80 х патч стикер
3508*2480
Мемфис шаблон 80 х 90 х годов стилей фона векторные иллюстрации
4167*4167
green environmental protection pattern garbage can be recycled green clean
2000*2000
три группы 3d реалистичное декоративное яйцо с золотым цветом на гнезде bd с золотым всплеском текстовый баннер
5000*5000
80 основных форм силуэта
5000*5000
80 летний юбилей дизайн шаблона векторные иллюстрации
4083*4083
дизайн плаката премьера фильма кино с белым вектором экрана ба
1200*1200
поп арт 80 х патч стикер
3508*2480
Мемфис бесшовные модели 80 х 90 х стилей
4167*4167
мемфис бесшовной схеме 80s 90 все стили
4167*4167
3d Изометрические номера 76 80
1200*1200
скейтборд в неоновых цветах 80 х
1200*1200
Минимализм Супер Продажа до 80 ramadan label
2000*2000
80 е брызги краски дизайн текста
1200*1200
3d визуализация текста 80 процентов от большой продажи
1200*1200
пентаграмма наклейки 80 х мультик звезд мультика стикер
2003*2003
поп арт 80 х патч стикер
3508*2480
чат комментарий образование синий значок на абстрактных облако сообщение
5556*5556
al ba ith 99 ИМЯ АЛЛАХ
1200*1200
ценю хорошо как плоская цвет значок векторная icon замечания
5556*5556
число 80
2000*2000
ba угол звезда голографическая радуга лазерная наклейка
1200*1200
Красивая розовая и безупречная воздушная подушка bb крем косметика постер розовый красивый розовый Нет времени На воздушной
3240*4320
Векторная иллюстрация мультфильм различных овощей на деревянном ба
800*800
Мемфис шаблон 80 х 90 х годов на белом фоне векторная иллюстрация
4167*4167
поп арт 80 х патч стикер
2292*2293
80 летие векторный дизайн шаблона иллюстрация
4167*4167
blue series frame color can be changed text box streamer
1024*1369
Персонаж из партии 80 х годов
1200*1200
поп арт 80 х патч стикер
3508*2480
prohibited use mobile phone illustration can not be used
2048*2048
цвет перо на воздушной подушке bb крем трехмерный элемент
1200*1200
поп арт 80 х патч стикер
3508*2480
но логотип компании вектор дизайн шаблона иллюстрация
4083*4083
Косметический bb Крем Дизайн Плаката косметический Косметика постер Реклама косметики Плакат
3240*4320
be careful to slip fall warning sign carefully
2500*2775
ретро стиль 80 х годов диско дизайн неон плакат
5556*5556
милая ретро девушка 80 х 90 х годов
800*800
Ретро мода неоновый эффект 80 х тема художественное слово
1200*1200
Ручная роспись борода ба zihu большая борода
1200*1200
Ретро ТВ игра 80 х годов в стиле арт дизайн
1200*1200
простая инициализация bb b геометрическая линия сети и логотип цифровых данных
2276*2276
Кассета для вечеринок в стиле ретро 80 х
1200*1200
Ретро мода 80 х градиент цвета художественного слова
1200*1200
bd письмо 3d круг логотип
1200*1200
80 х годов ретро слово градиент цвета искусства
1200*1200
смысл, история, фото рисунков, эскизы
Тут вы прочитаете все самое важное про значение тату «треугольник и круг», варианты и особенности рисунков, сможете выяснить их смысл, толкование, историю появления.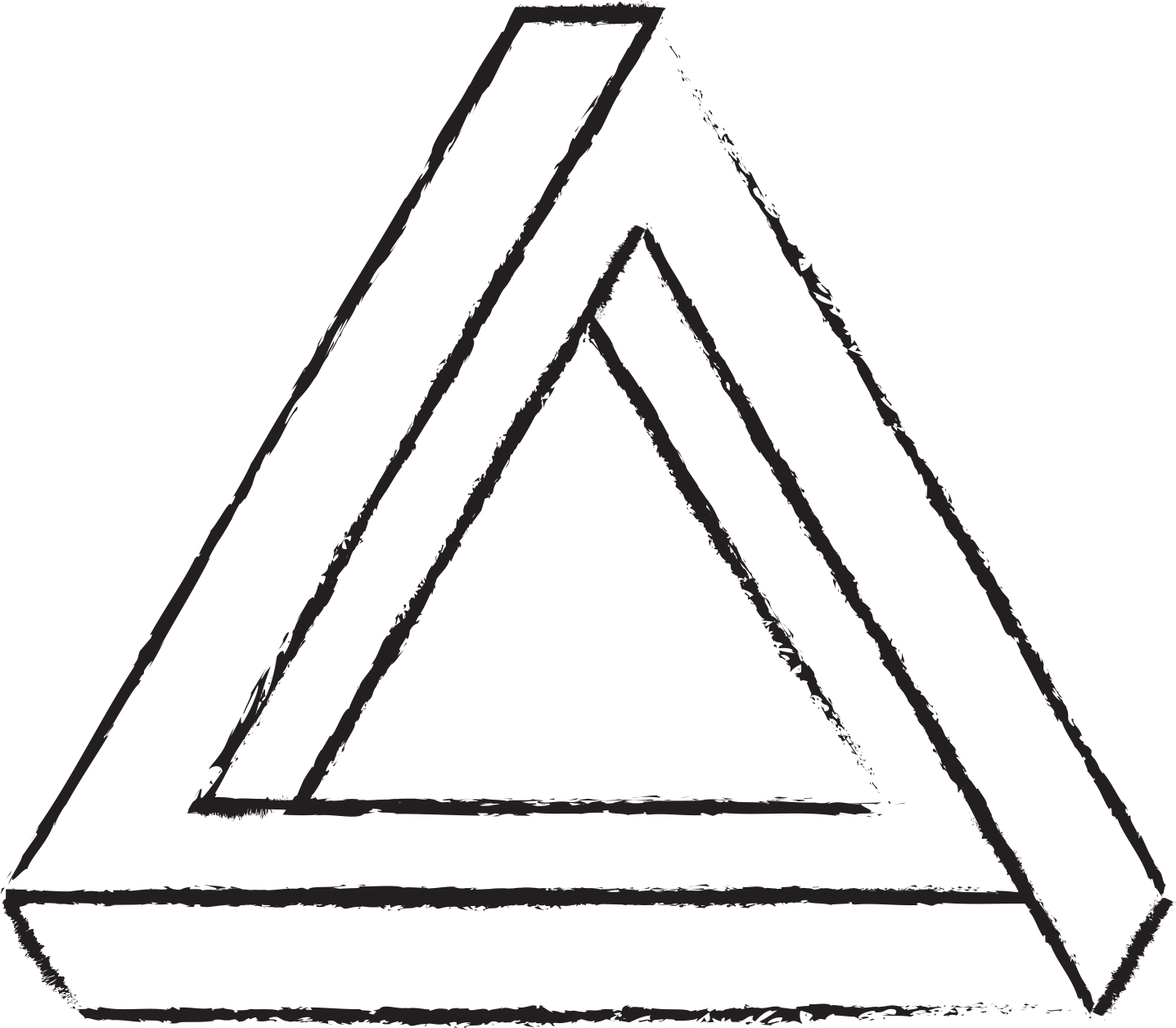
Больше примеров мы собрали для вас тут:
- Фото тату «треугольник и круг»
- Эскизы тату «треугольник и круг»
Все про варианты рисунка, особенности и значение тату «треугольник и круг»
Среди татуировок можно найти самый подходящий рисунок на собственные вкус и цвет. Поскольку с тату хозяину потом жить и жить, выбор и образ татуировки индивидуальный. Причём татуировка – это не только рисунок. Это обозначение чего-либо. В каждой тату есть смысл, значение, олицетворение или же просто какой-либо знак. И, чтобы знать, о чём тату, надо тратить много времени на чтение литературы, тратить на поиски информации уйму времени. Но, чтобы облегчить выбор рисунка, расскажем об одном из многочисленных и очень популярных рисунков под названием «Круг в треугольнике».
Казалось бы, просто треугольник, круг и, возможно, что-то ещё вдобавок, линия, в пример.
Тут не так сложно и абсурдно, как с чёрным квадратом всеми известного Малевича. На самом же деле тату символизирует несколько значений сразу. Да, бывает и такое. Пройдёмся по порядку.
Фото готовых рисунков татуировки «треугольник и круг»:
Во-первых, по одной из версий, человек – это часть Вселенной, это роль человека в ней. Также каждый человек является маленькой Вселенной в самом себе, с чем сложно не согласиться.
Во-вторых, по иному замыслу, этот символ обладает некой магией, силами духов, природы. Для особого ритуала (экзорцизм), после которого злые Духи обладают возможностью покинуть человека, как раз-таки необходим этот символ.
В-третьих, ещё знак есть в литературе, кино. Например, произведение «Гарри Поттер», в котором один из героев обладал клоном с таким символом. По сюжету это означает Дары смерти.
И в-четвёртых. Даже история не осталась в стороне. По слухам, давний правитель Израиля, Соломон, пользовался магией, включая и круг с треугольником, чтобы облегчить решение той или иной проблемы. Как говорится, на войне все способы хороши! Причём это очень даже хорошее средство решения проблем, если, конечно, уметь правильно использовать его. Соломон не один такой умный. Есть и другие исторические примеры, но они не особо важны. Главное, что и история имеет отношение к магии и этому замечательному символу – круг в треугольнике.
В-пятых, напоследок ещё одно из многочисленных значений. Тоже немного связано с волшебством. Человек с этим тату принимает триединственные принципы, принимая веру в последующие возрождения. Также он принимает цикличность развития природы, веря в божественность всех живых, полностью доверяя своей и только своей судьбе.
И каким бы не стал Ваш выбор, пусть он будет обдуманным, рисунок будет неповторимым и красивым! Красочной всем татуировок! И помните, что татуировки потом останутся на долго, если не навсегда, именно поэтому не стоит несерьёзно относиться к выбору.
Смотреть видео:
Вы можете посмотреть:
ЭСКИЗ ТАТУ ТРЕУГОЛЬНИК И КРУГ
ФОТО ТАТУ ТРЕУГОЛЬНИК И КРУГ
Символ треугольник | Истории плюс рисунки
Любой инженер вам скажет, что треугольник – жесткая фигура, она не подвержена деформации. Опорные конструкции стараются делать так, чтобы в них присутствовали треугольники. А вот что такое треугольник с символической точки зрения? Эта фигура часто встречается на религиозных и эзотерических изображениях. Что она означает?
Возможно, физическое свойство жесткости треугольника, которое часто используют в строительстве, связано и с ментальным значением фигуры. Это некая основа, фундаментальный образ. Он присутствует в религиях, философии, эзотерике.
Значение в религии и философии
Платон говорил, что поверхность состоит из треугольников, подразумевая этим, что площадь любой плоской фигуры можно измерить, разбив ее на треугольники.
В Древнем Египте прямоугольный треугольник с соотношением сторон 3:4:5 являлся крайне важным, так как помогал точно построить прямой угол. Вертикальная его сторона символизировала мужчину, горизонтальная – женщину, а гипотенуза (наклонная) – их потомство.
В религии треугольник обозначает единение тела, души и духа.
Есть и такое объяснение – время, пространство и универсум (система объектов).
Три треугольника – это целостность и совершенство вселенной.
Треугольник в круге – упорядоченность мира в окружении хаоса.
Любое тройственное понятие можно представить в образе треугольника. Ему соответствует цифра три.
Три сплетенных треугольника – валькнут древнескандинавский символ (бога Одина). Одно из значений – объединение прошлого, настоящего и будущего. Еще одно – девять миров, в которые дается доступ.
Всевидящее око – это изображение глаза в треугольнике. Это масонский символ, который обозначает Великого Архитектора (считай Бога), наблюдающего за деяниями вольных каменщиков (масонов).
Символ также носит название «лучезарная дельта».
Такой же образ всевидящего ока присутствует и в христианстве, означая практически то же, что и в масонстве. Фактически, как ни крути, он означает, что Творец все видит, что делает человек. Стало быть, нам за все придется отвечать. И мы еще при этом остерегаемся наблюдения в глобальной сети. Да что оно значит вообще, по сравнению с Таким! Высшим наблюдением. Хотя, везде есть свои нюансы.
Звезда Давида
Два равносторонних треугольника, пересекающихся так, что они образуют гексаграмму (шесть углов), называются звездой Давида (или щитом Давида). Это довольно древний символ. Гексаграмма – шестиконечная звезда, в отличие от пентаграммы – пятиконечной звезды. Иногда этот символ называют также печатью царя Соломона. Это еврейский символ, но он встречается и на эмблемах некоторых других государств, городов.
Гексаграмма встречается в Древней Индии, и похоже, появилась там еще раньше, чем на Ближнем Востоке и в Европе. Встречается символ у римлян, у кельтов и многих других народностей.
В средние века его активно использовали алхимики. Такой знак можно встретить на печатях европейский правителей, принадлежащих христианской церкви. Есть он в арабских книгах. Значение его порой меняется, но везде он призван работать в качестве амулета, некой защиты, магической силы.
Причиной такой популярности, несомненно, является использование двух треугольников – сильных, жестких, фундаментальных фигур.
Трактовок гексаграммы множество. Есть мнение, что это объединение женского и мужского начала. Второе предположение – объединение небесного и земного.
Третье объяснение символа – объединение четырех стихий: двух нижних (земля и вода), и двух высоких (воздух, огонь).
Шестиконечная звезда может также означать управление всем миром – всеми четырьмя сторонами света.
Согласно каббале – это символ семи сфирот (шесть треугольников и центр). Идеальные цифры или сферы, образующие царство проявления Бога. Там вообще все сложно.
Есть и другие толкования.
В основном они связаны с религиозными или философскими размышлениями на этот счет.
Орнаменты с треугольниками
Треугольник – одна из первых геометрических фигур, встречающихся в орнаментах. Нарисовать с ее помощью можно много чего красивого.
Треугольник Пенроуза — пример невозможной фигуры.
Вообще же сила любой фигуры или символа зависит от того, как мы ее применим, и какое значение вложим. Ка по мне, лучше рисовать из них узоры и применять в строительстве.
Высоты медианы биссектрисы треугольника — материалы для подготовки к ЕГЭ по Математике
Высоты, медианы и биссектрисы треугольника постоянно встречаются нам в задачах по геометрии. Мы начнем с таблицы, в которой показано, что такое высоты, медианы и биссектрисы, и какими свойствами они обладают. Затем — подробные объяснения и решение задач.
Напомним, что высота треугольника — это перпендикуляр, опущенный из его вершины на противоположную сторону.
Три высоты треугольника всегда пересекаются в одной точке. Вот как это выглядит в случае остроугольного треугольника.
Попробуйте провести три высоты в тупоугольном треугольнике. Получилось? Да, редкий выпускник справляется с этим заданием. Действительно, мы не можем опустить перпендикуляр из точки на отрезок , зато можем опустить его на прямую — то есть на продолжение стороны .
В этом случае в одной точке пересекаются не сами высоты, а их продолжения.
А как выглядят три высоты в прямоугольном треугольнике? В какой точке они пересекаются?
Медиана треугольника — отрезок, соединяющий его вершину с серединой противоположной стороны.
Три медианы треугольника пересекаются в одной точке и делятся в ней в отношении , считая от вершины.
Биссектриса треугольника — отрезок, соединяющий вершину треугольника с точкой на противоположной стороне и делящий угол треугольника пополам.
У биссектрисы угла есть замечательное свойство — точки, принадлежащие ей, равноудалены от сторон угла. Поэтому три биссектрисы треугольника пересекаются в одной точке, равноудаленной от всех сторон треугольника. Эта точка является центром окружности, вписанной в треугольник.
Еще одно свойство биссектрисы пригодится тем, кто собирается решать задачу . Биссектриса треугольника делит противоположную сторону в отношении длин прилежащих сторон.
Ты нашел то, что искал? Поделись с друзьями!
Разберем несколько задач, в которых речь идет о высотах, медианах и биссектрисах треугольника. Все задачи взяты из Банка заданий ФИПИ.
1. Найдите острый угол между биссектрисами острых углов прямоугольного треугольника. Ответ дайте в градусах.
Пусть биссектрисы треугольника (в котором угол равен ) пересекаются в точке .
Рассмотрим треугольник .
,
, тогда
Острый угол между биссектрисами на рисунке обозначен .
Угол смежный с углом , следовательно, .
Поскольку треугольник — прямоугольный, то .
Тогда .
Ответ: .
2. Острые углы прямоугольного треугольника равны и . Найдите угол между высотой и биссектрисой, проведенными из вершины прямого угла. Ответ дайте в градусах.
Пусть — высота, проведенная из вершины прямого угла , — биссектриса угла .
Тогда
.
Угол между высотой и биссектрисой — это угол .
Ответ: .
3. Два угла треугольника равны и . Найдите тупой угол, который образуют высоты треугольника, выходящие из вершин этих углов. Ответ дайте в градусах.
Из треугольника (угол — прямой) найдем угол . Он равен .
Из треугольника ( — прямой) найдем угол . Он равен .
В треугольнике известны два угла. Найдем третий, то есть угол , который и является тупым углом между высотами треугольника :
.
Ответ: .
4. В треугольнике угол равен , и — биссектрисы, пересекающиеся в точке .
Найдите угол . Ответ дайте в градусах.
Пусть в треугольнике угол равен , угол равен .
Рассмотрим треугольник .
, тогда .
Из треугольника получим, что .
Тогда .
Ответ: .
5. В треугольнике угол равен , угол равен . , и — биссектрисы, пересекающиеся в точке . Найдите угол . Ответ дайте в градусах.
Найдем угол . Он равен .
Тогда .
Из треугольника найдем угол . Он равен .
Рассмотрим треугольник .
, . Значит
Ответ: .
6. В треугольнике , — медиана, угол равен , угол равен . Найдите угол . Ответ дайте в градусах.
Как решать эту задачу? У медианы прямоугольного треугольника, проведенной из вершины прямого угла, есть особое свойство. Мы докажем его в теме «Прямоугольник и его свойства».
Подсказка: Сделайте чертеж, найдите на нем равнобедренные треугольники и докажите, что они равнобедренные.
Правильный ответ: .
Рисунок из трех треугольников
Этот видеоурок доступен по абонементу
У вас уже есть абонемент? Войти
Рис. 1. Иллюстрация к примеру
Мы видим, что фигуры № 1, 2, 3, 5 – четырехугольники. Каждая из них имеет свое название (рис. 2).
Рис. 2. Четырехугольники
Значит, «лишней» фигурой является треугольник (рис. 3).
Рис. 3. Иллюстрация к примеру
Треугольником называется фигура, которая состоит из трех точек, не лежащих на одной прямой, и трех отрезков, попарно соединяющих эти точки.
Точки называются вершинами треугольника, отрезки – его сторонами. Стороны треугольника образуют в вершинах треугольника три угла.
Знакомство с основными свойствами треугольника
Основными признаками треугольника являются три стороны и три угла. По величине угла треугольники бывают остроугольные, прямоугольные и тупоугольные.
Знакомство с видами треугольников по величине угла
Треугольник называется остроугольным, если все три угла его острые, то есть меньше 90° (рис. 4).
Рис. 4. Остроугольный треугольник
Треугольник называется прямоугольным, если один из его углов равен 90° (рис. 5).
Рис. 5. Прямоугольный треугольник
Треугольник называется тупоугольным, если один из его углов тупой, то есть больше 90° (рис. 6).
Рис. 6. Тупоугольный треугольник
Знакомство с видами по числу равных сторон
По числу равных сторон треугольники бывают равносторонние, равнобедренные, разносторонние.
Равнобедренным называется треугольник, у которого две стороны равны (рис. 7).
Рис. 7. Равнобедренный треугольник
Эти стороны называются боковыми, третья сторона – основанием. В равнобедренном треугольнике углы при основании равны.
Равнобедренные треугольники бывают остроугольными и тупоугольными (рис. 8).
Рис. 8. Остроугольный и тупоугольный равнобедренные треугольники
Равносторонним называется треугольник, у которого все три стороны равны (рис. 9).
Рис. 9. Равносторонний треугольник
В равностороннем треугольнике все углы равны. Равносторонние треугольники всегда остроугольные.
Разносторонним называется треугольник, у которого все три стороны имеют разную длину (рис. 10).
Рис. 10. Разносторонний треугольник
Выполнение тренировочных упражнений, деление на группы
Выполните задание. Распределите данные треугольники на три группы (рис. 11).
Рис. 11. Иллюстрация к заданию
Сначала распределим по величине углов.
Остроугольные треугольники: № 1, № 3.
Прямоугольные треугольники: № 2, № 6.
Тупоугольные треугольники: № 4, № 5.
Эти же треугольники распределим на группы по числу равных сторон.
Разносторонние треугольники: № 4, № 6.
Равнобедренные треугольники: № 2, № 3, № 5.
Равносторонний треугольник: № 1.
Решение геометрической задачи
Подумайте, из какого куска проволоки сделали каждый треугольник (рис. 12).
Рис. 12. Иллюстрация к заданию
Можно рассуждать так.
Первый кусок проволоки разделен на три равные части, поэтому из него можно сделать равносторонний треугольник. На рисунке он изображен третьим.
Второй кусок проволоки разделен на три разные части, поэтому из него можно сделать разносторонний треугольник. На рисунке он изображен первым.
Третий кусок проволоки разделен на три части, где две части имеют одинаковую длину, значит, из него можно сделать равнобедренный треугольник. На рисунке он изображен вторым.
Сегодня на уроке мы познакомились с различными видами треугольников.
Список литературы
- М.И. Моро, М.А. Бантова и др. Математика: Учебник. 3 класс: в 2-х частях, часть 1. – М.: «Просвещение», 2012.
- М.И. Моро, М.А. Бантова и др. Математика: Учебник. 3 класс: в 2-х частях, часть 2. – М.: «Просвещение», 2012.
- М.И. Моро. Уроки математики: Методические рекомендации для учителя. 3 класс. – М.: Просвещение, 2012.
- Нормативно-правовой документ. Контроль и оценка результатов обучения. – М.: «Просвещение», 2011.
- «Школа России»: Программы для начальной школы. – М.: «Просвещение», 2011.
- С.И. Волкова. Математика: Проверочные работы. 3 класс. – М.: Просвещение, 2012.
- В.Н. Рудницкая. Тесты. – М.: «Экзамен», 2012.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
Домашнее задание
1. Закончите фразы.
а) Треугольником называется фигура, которая состоит из …, не лежащих на одной прямой, и …, попарно соединяющих эти точки.
б) Точки называются …, отрезки – его …. Стороны треугольника образуют в вершинах треугольника ….
в) По величине угла треугольники бывают … , … , … .
г) По числу равных сторон треугольники бывают … , … , … .
а) прямоугольный треугольник;
б) остроугольный треугольник;
в) тупоугольный треугольник;
г) равносторонний треугольник;
д) разносторонний треугольник;
е) равнобедренный треугольник.
3. Составьте задание по теме урока для своих товарищей.
Если вы нашли ошибку или неработающую ссылку, пожалуйста, сообщите нам – сделайте свой вклад в развитие проекта.
Главное нужно указать файл картинки на вашем компьютере или телефоне, нажать кнопку ОК. Остальные настройки выставлены по умолчанию.
Пример фотографии розы без изменений и сделанная на этом сайте картинка из треугольников:
Обратите внимание, что обработка длится около 1 минуты, на выходе получается картинка из треугольников не более 0.5 мегапикселей, примерно 800×600 и этого размера хватит с запасом, например, чтобы выложить на сайте vk.com. Если нужна картинка из треугольников без уменьшения, то присылайте на контактный ящик фото или картинку, которую нужно обработать и выставленные настройки (если они изменялись) — будет сделано бесплатно в течение суток.
Ещё картинку можно сделать из: квадратов | треугольников | кругов | звёзд
Исходное изображение никак не изменяется. Вам будет предоставлена другая обработанная картинка.
Веселые и красочные задания для детей «Рисунки из геометрических фигур» являются очень удобным обучающим материалом для детей дошкольного и младшего школьного возраста по изучению и запоминанию основных геометрических форм: треугольника, круга, овала, квадрата, прямоугольника и трапеции. Все задания предназначены для самостоятельной работы ребенка под наблюдением взрослых. Родитель или педагог должны правильно объяснить ребенку, что он должен сделать в каждом задании.
Также вам может понравиться наш онлайн тренажер по математике для 1 класса «Геометрические фигуры»:
Геометрические фигуры 1 класс — Онлайн-тренажер
Онлайн-тренажер по математике «Геометрические фигуры 1 класс» поможет первоклассникам потренироваться в умении различать основные геометрические фигуры: квадрат, круг, овал, прямоугольник и треугольник.
1. Рисунки из геометрических фигур — Условия к выполнению заданий:
Чтобы начать выполнять задания, скачайте во вложениях бланк, в котором вы найдете 2 типа заданий: рисунки из геометрических фигур для раскрашивания и задание для рисования фигур с помощью логического и образного мышления. Распечатайте скачанную страницу на цветном принтере и дайте ребенку вместе с цветными карандашами или фломастерами.
- В первом задании малышу нужно мысленно соединить каждые две части представленных фигур в одну и нарисовать полученную геометрическую форму в соответствующей клетке. Объясните ребенку, что детали можно поворачивать в уме в разные стороны до тех пор, пока он не получит нужную комбинацию для составления фигуры. Например, два треугольника можно повернуть так, чтобы получился квадрат. После этого квадрат нужно нарисовать в клетке рядом с треугольником. По такому же принципу необходимо сделать и остальные рисунки.
- Во втором задании дети должны правильно назвать фигуры из которых состоят нарисованные картинки. Затем эти картинки нужно раскрасить, используя цвета рядом с геометрическими фигурами. Каждую фигуру нужно раскрасить только в указанный цвет.
Чтобы придать занятию больше энергии и энтузиазма — можно объединить несколько детей в группу и предоставить им выполнение заданий на время. Тот ребенок, который первый выполнит все задания без ошибок, признается победителем. В качестве приза можно повесить его работу на стену достижений (такая стена обязательно должна присутствовать как дома, так и в детском саду).
Скачать задание «Рисунки из геометрических фигур» вы можете во вложениях внизу страницы.
2. Геометрические фигуры в рисунках — 3 задания-раскраски:
Следующее занятие также скрывает основные геометрические фигуры в рисунках. Ребенку нужно найти эти фигуры, назвать их, а затем раскрасить таким образом, чтобы каждой фигуре соответствовал определенный цвет (руководствуясь инструкцией на бланке с заданием).
Во втором задании нужно нарисовать на всех этажах любые геометрические фигуры, но при этом необходимо соблюдать условие: на каждом этаже фигуры должны находиться в разном порядке. В последствии можно это задание видоизменить. Для этого достаточно начертить на бумаге точно такой домик и попросить ребенка заполнить его фигурами так, чтобы в каждом подъезде не встречались одинаковые фигуры (подъезд — вертикальный ряд квадратов).
В третьем задании нужно, руководствуясь стрелками, нарисовать точно такие же геометрические фигуры внутри или снаружи данных фигур.
Не торопите ребенка и не подсказывайте ему, пока он сам вас об этом не попросит. Если у малыша что-то получилось неправильно — вы всегда можете распечатать еще один экземпляр учебного бланка с заданием.
Скачать задание «Геометрические фигуры в рисунках» вы можете во вложениях внизу страницы.
3. Развивающая раскраска для детей — Смешные рисунки из фигур
В этом занятии детям опять предстоит отыскать геометрические фигуры среди рисунков. После предыдущих занятий им будет уже легче ориентироваться в знакомых формах, так что, я думаю, оба задания не вызовут у них затруднений.
Второе задание также дает возможность малышу повторить математические знаки и усвоить счет до десяти, так как ему понадобится посчитать количество фигур и поставить знаки «больше» «меньше» между картинками.
Скачать раскраску «Смешные рисунки из фигур» вы можете во вложениях внизу страницы.
Также вам будут полезны и другие материалы по изучению геометрических фигур:
Здесь вы с ребенком можете изучить геометрические фигуры и их названия с помощью веселых заданий в картинках.
Задания ознакомят ребенка с основными фигурами геометрии — кругом, овалом, квадратом, прямоугольником и треугольником. Только здесь не занудное зазубривание названий фигур, а своеобразная игра-раскраска.
Как правило, геометрию начинают изучать, рисуя плоские геометрические фигуры. Восприятие правильной геометрической формы невозможно без выведения ее своими руками на листе бумаги.
Это занятие изрядно позабавит ваших юных математиков. Ведь теперь им придется находить знакомые формы геометрических фигур среди множества картинок.
Наложение фигур друг на друга — это занятие по геометрии для дошкольников и младших школьников. Смысл упражнения состоит в решении примеров на сложение. Только это необычные примеры. Вместо цифр здесь нужно складывать геометрические фигуры.
Это задание составлено в виде игры, в которой ребенку предстоит менять свойства геометрических фигур: форму, цвет или размер.
Здесь вы можете скачать задания в картинках, в которых представлен счет геометрических фигур для занятий по математике.
В этом задании ребенок познакомится с таким понятием, как чертежи геометрических тел. По сути, это занятие представляет собой мини-урок по начертательной геометрии
Здесь мы подготовили для вас объемные геометрические фигуры из бумаги, которые нужно вырезать и склеить. Куб, пирамиды, ромб, конус, цилиндр, шестигранник, распечатать их на картоне (или цветной бумаге, а затем наклеить на картон), а затем дать ребенку для запоминания.
Дети любят раскрашивать и обводить, поэтому данные задания сделают ваши занятия по обучению счету максимально эффективными.
И еще можете поиграть в математические игры онлайн от лисенка Бибуши:
В этой развивающей онлайн игре ребенку предстоит определить, что является лишним среди 4 картинок. При этом необходимо руководствоваться признаками геометрических форм.
«>
MAU ГЛОССАРИЙ ИСКУССТВА И ДИЗАЙНА ｜ Университет искусств Мусасино
Треугольник — это инструмент для рисования, используемый для рисования точных параллельных линий, вертикальных линий и других наклонных линий. Как правило, два прямоугольных треугольных элемента с разными углами образуют один набор. На одной детали углы составляют 90 °, 60 ° и 30 °; с другой стороны, образуется равнобедренный треугольник с углами 90 °, 45 ° и 45 °. Один масштабируется; другой нет. Некоторые прозрачные треугольники из пластика и акрила имеют решетки. Помимо пластиковых и акриловых треугольников, есть еще треугольники из нержавеющей стали и дерева.Размеры треугольников различаются, но для черчения обычно от 10 см до 40 см. Треугольники большего размера часто используются для рисования линий на доске в классах начальной школы.
Когда вы используете треугольник для рисования горизонтальных или вертикальных линий, вам нужно использовать два треугольника вместе в тандеме. Комбинируя их, вы можете рисовать линии под углами 30 °, 45 °, 60 ° и 90 °. Вы также можете использовать треугольник в тандеме с Т-образным квадратом. Например, чтобы провести параллельные линии, надежно скрепите две линейки вместе, а затем переместите линейку с правой стороны вниз от вершины, проведя линию слева направо.См. Схему этой процедуры на рисунке.
Треугольник впервые появляется в литературе раннего периода Мэйдзи под названием «треугольный правитель» (санкакуки). В то время он в основном использовался для наблюдения за прямыми углами и, таким образом, имел пестрый ассортимент других маркировок, отличных от прямого угла, но в середине периода Мэйдзи люди начали использовать треугольники в двух комбинациях — 90 °, Углы 60 °, 30 ° и углы 90 °, 45 °, 45 ° — которые мы видим сегодня для рисования горизонтальных, вертикальных и диагональных линий.
Существует также другой вид линейки, которая напоминает треугольник и может рисовать линии с одинаковым углом: регулируемый треугольник. Сделанный из двух подвижных треугольных частей, соединенных на градуированной доске с прикрепленным к ней транспортиром, регулируемый треугольник позволяет художнику регулировать углы двух частей, используя градацию. Можно сделать разные углы, сочетая углы с треугольником. Однако при использовании регулируемого треугольника вы можете рисовать другие дополнительные угловые линии, а также измерять углы.Треугольники, используемые для других целей рисования, включают навигационные треугольники, которые помогают пользователям читать навигационные карты. Треугольники, регулируемые треугольники и другие подобные инструменты доступны для покупки в магазинах канцелярских товаров, художественных принадлежностей и других магазинах, занимающихся разработкой товаров.
Начните с данного отрезка линии и двух углов. | Примечание: Два заданных угла служат только для обозначения меры двух углов. Линии, образующие данные углы, имеют случайную длину, не имеющую значения при построении. |
| Первая часть этой конструкции (шаги 1–4) — скопировать линейный сегмент в образуют одну сторону нового треугольника. (См. Копирование сегмента линии). | |
| 1. Отметьте точку A, которая будет одной вершиной нового треугольника. | |
| 2. Установите ширину циркуля на длину отрезка AB. | |
| 3. С помощью циркуля на A нарисуйте дугу возле будущей вершины B треугольника. | |
| 4. Отметьте точку B на этой дуге. Затем проведите линию AB. Это будет одна сторона нового треугольника. | |
| Сейчас мы по сути копируем два угла.(См. Копирование угла). | |
| 5. С помощью циркуля любой удобной ширины проведите дугу через обе линии с заданным углом A. | |
| 6. Не меняя ширины циркуля, нарисуйте дугу в точке A на новом треугольнике. Дуга должна пересекать AB и также пересекать будущую сторону треугольника. | |
| 7. Установите циркуль на ширину дуги под заданным углом A.Это расстояние между точками, где дуга пересекает стороны угла. | |
| 8. Ближайшая точка A нарисуйте дугу в аналогичном месте, чтобы она пересекала дугу, нарисованную ранее. Это, по сути, «копирует» угол в точке P в угол в точке A. | |
| 9. Проведите линию от A через точку пересечения дуг. Это станет второй стороной треугольника. Рисуем долго. | |
| 10. Повторите этот процесс для B. Копирование угловой меры из данного угла B в новый треугольник в B. Точка пересечения линий — C, третья вершина треугольника. | |
| Готово. У синего треугольника ABC есть сторона и два желаемых угла. | |
Рисование треугольников — углы и многоугольники — Mathigon
В этом разделе мы рассмотрим, как рисовать треугольники.Например, если я дам вам три числа, сможете ли вы сделать треугольник с такой длиной сторон?
Вот несколько примеров — перемещайте вершины треугольника, пока три стороны не совпадут с одной из троек слева.
Похоже, есть несколько случаев, когда три числа просто не могут образовать треугольник. Это особенно происходит, когда одна сторона намного длиннее, чем намного короче, чем длина двух других.
Представьте, что три стороны треугольника представляют собой металлические стержни, соединенные петлями.Поместим самый длинный стержень посередине, а более короткий — по бокам.
Теперь легко увидеть, что невозможно соединить концы более коротких стержней, если их общая длина меньше, чем длина большего стержня. Продолжить
Давайте перепишем это наблюдение в математических терминах:
Неравенство треугольника
Сумма длин любых двух сторон треугольника должна быть больше длины третьей.
Другими словами, если треугольник имеет стороны a , b и c , то мы знаем, что a + b> c и a + c> b и b + c> a.
Неравенство треугольника позволяет нам быстро проверить, могут ли три числа составить треугольник. Какие из этих троек возможны?
Неравенство треугольника также позволяет нам оценить длину третьей стороны треугольника, если мы знаем длину двух других.
Представьте, что треугольник имеет две стороны длиной 4 и 6. Назовем c длиной третьей стороны. Тогда мы знаем, что
4 + 6> c, 4 + c> 6 и 6 + c> 4
Мы можем изменить эти неравенства так, чтобы получить
И снова мы можем думать об этом, используя физические объекты: две стороны треугольника — это металлические стержни длиной 4 и 6, а третья сторона — резина. группа, которая может расширяться или сжиматься.
Теперь вы можете видеть, что длина резинки всегда будет не менее 6−4 = 2 и не более 6 + 4 = 10.
Обратите внимание, что это строгих неравенств . Если третья сторона равна , точно 2 или 10, мы получим прямую линию, а не треугольник.Однако 2,1 или 9,9 будет достаточно, чтобы образовался треугольник.
СКОРО В НАЛИЧИИ — Подробнее о рисовании треугольников, углах в треугольниках, сходстве и конгруэнтности.
7.2.4: Рисование треугольников (часть 1)
Урок
Давайте посмотрим, сколько разных треугольников мы можем нарисовать с определенными размерами.
Упражнение \ (\ PageIndex {1} \): какое из них не принадлежит: треугольники
Какой из них не принадлежит?
Рисунок \ (\ PageIndex {1} \): четыре треугольника A, B, C, D.Треугольник A имеет 3 угла по 60 градусов и 2 стороны с длиной 3. Треугольник B имеет углы, обозначенные как 130 градусов, 20 градусов, а длина стороны между ними 7. Треугольник C имеет две стороны длиной 9, угол 55 градусов. Треугольник D имеет один угол 90 градусов.Упражнение \ (\ PageIndex {2} \): совпадает ли ваш треугольник с их?
Трое учеников нарисовали треугольник. За каждое описание:
- Перетащите вершины, чтобы создать треугольник с заданными размерами.
- Обратите внимание на разные длины сторон и размеры углов в вашем треугольнике.
- Решите, должен ли нарисованный вами треугольник быть идентичной копией треугольника, нарисованного учеником. Объясните свои рассуждения.
Треугольник Джады имеет угол 75 °.
Треугольник Андре имеет один угол 75 ° и один угол 45 °.
Треугольник Лина имеет один угол 75 °, один угол 45 ° и одну сторону 5 см.
Упражнение \ (\ PageIndex {3} \): сколько вы можете нарисовать?
- Нарисуйте как можно больше разных треугольников с помощью каждого из этих наборов измерений:
- Два угла имеют размер \ (60 ^ {\ circ} \), а длина одной стороны 4 см.{\ circ} \), длина одной стороны — 4 см.
- Какие наборы измерений определяют один уникальный треугольник? Объясните или покажите свои рассуждения.
Вы готовы к большему?
Рисунок \ (\ PageIndex {2} \)На схеме 9 зубочисток используются для создания трех равносторонних треугольников. Придумайте способ переместить только 3 зубочистки так, чтобы на схеме было ровно 5 равносторонних треугольников.
Резюме
Иногда нам дают два разных размера угла и длину стороны, и невозможно нарисовать треугольник.{\ circ} \):
Рисунок \ (\ PageIndex {3} \): На рисунке нарисован горизонтальный линейный сегмент и помечен как 2. На левом конце линейного сегмента пунктирная линия проведена вверх и влево. Угол между пунктирной линией и горизонтальной линией обозначен как 120 градусов. На правом конце горизонтальной линии проведена пунктирная линия вверх и вправо. Угол между пунктирной линией и горизонтальной линией обозначен как 100 градусов.Иногда нам дают два разных размера угла и длину стороны между ними, и мы можем нарисовать уникальный треугольник.{\ circ} \) углы.
- Нарисуйте этот треугольник и пометьте свой эскиз заданными размерами.
- Сколько уникальных треугольников вы можете нарисовать таким образом?
Упражнение \ (\ PageIndex {6} \)
- Найдите значение для \ (x \), при котором \ (- x \) меньше \ (2x \).
- Найдите значение для \ (x \), которое делает \ (- x \) больше, чем \ (2x \).
(из блока 5.4.1)
Упражнение \ (\ PageIndex {7} \)
Одна из частиц в атомах называется электроном.Имеет заряд -1. Другая частица в атомах — протон. Имеет заряд +1.
Общий заряд атома — это сумма зарядов электронов и протонов. Вот список общих элементов.
| заряд от электронов | заряд от протонов | общий заряд | |
|---|---|---|---|
| углеродистый | \ (- 6 \) | \ (+ 6 \) | \ (0 \) |
| алюминий | \ (- 10 \) | \ (+ 13 \) | |
| фосфид | \ (- 18 \) | \ (+ 15 \) | |
| йодид | \ (- 54 \) | \ (+ 53 \) | |
| банка | \ (- 50 \) | \ (+ 50 \) |
Найдите общий заряд для остальных атомов в списке.
(из блока 5.2.2)
Упражнение \ (\ PageIndex {8} \)
Завод производит 3 бутылки газированной воды на каждые 7 бутылок простой воды. Если это единственные два продукта, которые они производят, какой процент их продукции составляет газированная вода? Какой процент просто?
(начиная с блока 4.1.3)
Многочисленные способы построения треугольника I
$ m_ {a}, m_ {b}, m_ {c} $
Через $ A $ и $ C $ нарисуйте линии, параллельные $ CM_ {c} $ и $ AM_ {a}, $, соответственно.Пусть $ P $ — точка пересечения. $ APCG $ — это параллелограмм, поэтому его диагонали делятся пополам из-за точки пересечения. Следовательно, они пересекаются в $ M_ {b}, $ и $ CM_ {b} $ — это медиана $ GPC. $ $ PC $ равен $ AG $ и параллелен ему, тогда как $ GM_ {a} $ составляет половину $ AG $ и, следовательно, $ PC. $ Следовательно, медиана $ GK $ для $ GPC $ параллельна $ BC $ и равна $ a / 2. $ Третья медиана в $ GPC $ аналогично параллельна $ AB $ и равна $ в / 2. $
Тогда есть строительство. Возьмите 2/3 доллара от каждой заданной медианы.Используйте $ SSS $, чтобы построить треугольник $ GPC. $ Найдите в этом треугольнике медианы. Удвойте их. Это даст три стороны искомого треугольника. Нарисуйте его снова, используя $ SSS. $
$ M_ {a}, M_ {b}, M_ {c}
$Треугольник $ M_ {a} M_ {b} M_ {c} $ похож на $ \ Delta ABC $ и вдвое меньше. Двойные его стороны. Затем используйте $ SSS $, чтобы построить $ ABC. $
$ a, b, m_ {c} $
Треугольник $ M_ {c} M_ {b} C $ имеет следующие стороны: $ a / 2, $ $ b / 2, $ $ m_ {c}. $ Следовательно, его можно построить с помощью $ SSS.$ Теперь увеличьте $ CM_ {b} $ до удвоенной длины, чтобы получить $ A. $ Затем увеличьте $ AM_ {c} $ до удвоенной длины, чтобы получить $ B. $
$ a, b, m_ {b}
$Треугольник $ BM_ {b} C $ состоит из следующих сторон: $ m_ {b}, $ $ b / 2, $ $ a. $ Мы можем построить его с помощью $ SSS. $ После этого расширить $ CM_ {b} $ в два раза больше длины, чтобы получить $ A. $
$ H_ {a}, H_ {b}, H_ {c}
$Треугольник $ H_ {a} H_ {b} H_ {c} $ известен как ортогональный треугольник $ \ Delta ABC. $ (Это треугольник педали ортоцентра.) Среди других интересных особенностей ортического треугольника можно отметить тот факт, что высоты $ \ Delta ABC $ являются биссектрисами угла $ H_ {a} H_ {b} H_ {c}. $ Чтобы доказать это, заметим, что $ HH_ {b } CH_ {a} $ — это четырехугольник, который можно вписать в круг диаметром $ CH $, потому что его два угла $ HH_ {b} C $ и $ HH_ {a} C $ правильные. Отсюда углы $ HH_ {a} H_ {b} $ и $ ACH $ равны. Однако $ ACH $ дополняет $ C $ в треугольнике $ ACH_ {c} $, а $ HH_ {a} H_ {b} $ дополняет $ H_ {b} H_ {a} C. $ Следовательно, последний равно $ C.$ Аналогично $ \ angle H_ {c} H_ {a} B = \ angle C. $ Что дает $ \ angle H_ {c} H_ {a} B = \ angle H_ {b} H_ {a} C. $ углы в $ H_ {b} $ и $ H_ {c} $ обрабатываются аналогичным образом.
Таким образом, мы получаем следующую конструкцию. Дан треугольник $ H_ {a} H_ {b} H_ {c}. $ Нарисуйте его биссектрисы. Через вершины проведите прямые, перпендикулярные соответствующим биссектрисам.
(Омар X. из старого CTKExchange отметил, что если все три точки различны, то конструкция фактически приводит к четырем решениям.Однако, имея в виду прямоугольные треугольники, проблема может иметь бесконечно много решений при условии, что две ножки совпадают.)
$ A, B, p $
Начните с рисования треугольника $ AB’C ‘$ с двумя заданными углами $ A $ и $ B. $ Как бы вы это ни сделали, полученный треугольник будет похож на треугольник $ \ Delta ABC $, который мы должны найти. На $ cc, $, начиная с точки $ A, $ измеряет перимитер $ p $ точек $ AB’C ‘$ (точка $ P) $ и $ 2p $ (точка $ Q). $ Соедините $ P $ и $ C ‘. $ Через $ Q проведите линию, параллельную $ PC’ $, которая пересекает $ bb $ в точке $ C.$ От $ C $ нарисуйте линию, параллельную $ C’B ‘$, чтобы получить $ B. $
Здесь уместно сделать замечание. Два угла полностью определяют форму треугольника . Для однозначного определения треугольника необходимо зафиксировать его размер . Поскольку в подобных треугольниках все линейные элементы находятся в одинаковом соотношении, любой линейный элемент в треугольнике однозначно определяет этот треугольник. Следовательно, вышеуказанное решение будет работать и в других случаях. Например, когда нам даны $ A, B, $ и, скажем, $ l_ {c} $ или $ H_ {a} M_ {b}.$
$ А, м_б, х_а $
Строительство принадлежит Рене Спербу.
Вершина $ A $ имеет своим локусом $ (O) $ с хордами $ BM_b $ длины $ m_b $, соединяющим угол $ A. $ Вершина $ C $ находится на $ AM_b $ на том же расстоянии от $ M_b $, что и $ A, $ означает, что геометрическое место точек $ C $ является окружностью $ (O ‘) $, симметричной $ (O) $ в $ M_b. $
Расстояние от середины $ M_b $ до стороны $ BC $ равно $ \ displaystyle \ frac {h_a} {2}. $ Отсюда следует, что основание перпендикуляра от $ M_b $ до $ BC $ лежит на пересечении окружности $ (BM_b) $ диаметром $ BM_b $ с кругом $ \ displaystyle C (M_b, \ frac {h_a} {2}).$ У двух окружностей всегда есть две точки пересечения. Обозначьте одну из них, скажем, $ X, $ и проведите линию $ BX. $ Эта линия пересекает окружность $ (O ‘) $ в одной (когда она касается окружности) или в двух точках. Любая из этих точек может служить вершиной $ C. $ После выбора вершина $ A $ будет найдена как второе пересечение $ CM_b $ и $ (O). $ Может быть $ 0,1,2,3,4 $ решения.
Открытые учебники | Сиявула
Математика
Наука
- Читать онлайн
Учебники
Английский
Класс 7A
Марка 7Б
7 класс (A и B вместе)
Африкаанс
Граад 7А
Граад 7Б
Граад 7 (A en B saam)
Пособия для учителя
- Читать онлайн
Учебники
Английский
Марка 8A
Сорт 8Б
Оценка 8 (вместе A и B)
Африкаанс
Граад 8А
Граад 8Б
Граад 8 (A en B saam)
Пособия для учителя
- Читать онлайн
Учебники
Английский
Марка 9А
Марка 9Б
9 класс (A и B вместе)
Африкаанс
Граад 9А
Граад 9Б
Граад 9 (A en B saam)
Пособия для учителя
- Читать онлайн
Учебники
Английский
Класс 4A
Класс 4Б
Класс 4 (вместе A и B)
Африкаанс
Граад 4А
Граад 4Б
Граад 4 (A en B saam)
Пособия для учителя
- Читать онлайн
Учебники
Английский
Марка 5А
Марка 5Б
Оценка 5 (вместе A и B)
Африкаанс
Граад 5А
Граад 5Б
Граад 5 (A en B saam)
Пособия для учителя
- Читать онлайн
Учебники
Английский
Марка 6А
Марка 6Б
6 класс (A и B вместе)
Африкаанс
Граад 6А
Граад 6Б
Граад 6 (A en B saam)
Пособия для учителя
Наша книга лицензионная
Эти книги не просто бесплатные, они также имеют открытую лицензию! Один и тот же контент, но разные версии (брендированные или нет) имеют разные лицензии, как объяснено:
CC-BY-ND (фирменные версии)
Вам разрешается и поощряется свободное копирование этих версий.Вы можете делать ксерокопии, распечатывать и распространять их сколько угодно раз. Вы можете скачать их на свой мобильный телефон, iPad, ПК или флешку. Вы можете записать их на компакт-диск, отправить по электронной почте или загрузить на свой веб-сайт. Единственным ограничением является то, что вы не можете адаптировать или изменять эти версии учебников, их содержание или обложки, поскольку они содержат соответствующие бренды Siyavula, спонсорские логотипы и одобрены Департаментом базового образования. Для получения дополнительной информации посетите Creative Commons Attribution-NoDerivs 3.0 Непортированный.
Узнайте больше о спонсорстве и партнерстве с другими, которые сделали возможным выпуск каждого из открытых учебников.
CC-BY (версии без марочного знака)
Эти небрендовые версии одного и того же контента доступны для вас, чтобы вы могли делиться ими, адаптировать, трансформировать, изменять или дополнять их любым способом, с единственным требованием — дать соответствующую оценку Siyavula. Для получения дополнительной информации посетите Creative Commons Attribution 3.0 Unported.
Как нарисовать невозможный треугольник
Легкое, пошаговое руководство по рисованию невозможного треугольникаНажмите ЗДЕСЬ, чтобы сохранить руководство в Pinterest!
Невозможный треугольник, также называемый треугольником Пенроуза или невозможным треугольником, был впервые нарисован шведским художником по имени Оскар Реутерсвард в 1934 году.
Он использовался в работах психиатра Лайонела Пенроуза, математика Роджера Пенроуза и голландского художника-математика М. Эшера, а также других художников.
Форма была описана как «невозможная в чистом виде».
Невозможный треугольник — это разновидность оптической иллюзии — изображение, которое из-за восприятия глазами и мозгом отличается от реальности.
Невозможные объекты — это оптические иллюзии, в которых двухмерная фигура (что-то плоское, например, рисунок на бумаге) интерпретируется мозгом как трехмерный объект — объект, который на самом деле не может существовать из-за своих физических пропорций.
Присмотритесь к невозможному треугольнику, и вы увидите, что его стороны необычным образом соединяются.
Прокрутите вниз, чтобы загрузить этот учебник в формате PDF.
В то время как невозможные объекты не могут существовать в реальном мире — вот почему их называют невозможными — художники приложили усилия, чтобы приблизить их.
Скульптура на открытом воздухе, показанная в Восточном Перте, Австралия, например, при взгляде под определенным углом принимает вид невозможного треугольника.
Однако, если смотреть под другим углом, становится очевидно, что линии «треугольника» на самом деле не соединяются.
Психологи и другие ученые издавна интересовались оптическими иллюзиями.
Леонардо да Винчи, возможно, был первым, кто нарисовал оптическую иллюзию, серию линий, которые, когда вы наклонили бумагу под правильным углом, превратились в глаз.
Исследователи говорят, что оптические иллюзии возникают потому, что когда наш мозг узнает о нашем окружении, он начинает делать предположения.Иногда эти предположения ошибочны, например, когда плоский рисунок выглядит трехмерным, и этот сдвиг может вызвать чувство замешательства.
Хотите нарисовать невозможный треугольник? Это не невозможно. На самом деле, это легко сделать с помощью этого простого пошагового руководства по рисованию.
Все, что вам понадобится, это карандаш, ручка или маркер и лист бумаги.
Вы также можете использовать линейку, чтобы рисовать прямые линии, и мелки, цветные карандаши или краски, чтобы закрасить законченный рисунок.
Если вам понравился этот урок, см. Также следующие руководства по рисованию: Кристалл, Звезда и Снежинка.
Разблокируйте БЕСПЛАТНЫЕ и ПЕЧАТНЫЕ уроки рисования и раскраски! Узнать большеПошаговые инструкции по рисованию невозможного треугольника
Рисование невозможного треугольника — шаг 11. Начните с рисования небольшого равностороннего треугольника, то есть треугольника со сторонами равной длины. Это сформирует отверстие в середине невозможного треугольника.
Рисование невозможного треугольника — шаг 22. Вытяните короткую прямую линию по диагонали от каждой точки треугольника. Эти линии образуют основу трехмерного изображения невозможного треугольника.
Рисование невозможного треугольника — шаг 33. От самой верхней диагональной линии проведите прямую линию, параллельную стороне маленького треугольника. Затем от этой линии проведите еще одну прямую, параллельную нижней части маленького треугольника.
Рисование невозможного треугольника — шаг 44.Нарисуйте прямую горизонтальную линию от самой нижней из исходных диагоналей. Эта линия должна быть параллельна двум другим горизонтальным линиям и на равном расстоянии от них.
Рисование невозможного треугольника — шаг 55. Проведите длинную прямую линию вверх от оставшейся диагональной линии, параллельную стороне маленького треугольника.
Рисование невозможного треугольника — шаг 66. Из самой верхней точки линии, проведенной на предыдущем шаге, проведите длинную прямую линию, параллельную противоположной стороне треугольника.
Рисование невозможного треугольника — шаг 77. От средней горизонтальной линии вытяните длинную прямую линию вверх, параллельно стороне существующего треугольника.
Рисование невозможного треугольника — шаг 88. Осталось только заключить фигуру невозможного треугольника. Начните с закрытия одного из углов короткой прямой линией.
Рисование невозможного треугольника — шаг 99. Используйте короткие прямые линии, чтобы обвести оставшиеся углы невозможного треугольника.
Завершите рисунок «Невозможный треугольник»10. Раскрасьте свой рисунок.
Готовы к другим геометрическим рисункам? Ознакомьтесь с нашими руководствами по рисованию кристаллов, снежинок и звезд.
Прокрутите вниз, чтобы загрузить этот учебник в формате PDF.
Учебник по рисованию для печати
УСТРАНЕНИЕ НЕПОЛАДОК УЧАСТНИКА
Все еще видите рекламу или не можете загрузить PDF-файл?
Сначала убедитесь, что вы вошли в систему.