Соотношение золотого сечения – Золотое сечение и симметрия — Мастерок.жж.рф — LiveJournal

Золотое сечение. Божественная пропорция – Ярмарка Мастеров

Золотое сечение (лат. Sectio aurea) — термин, знакомый многим. Освежим немного нашу память, друзья!

Золотое сечение, или золотая пропорция — идеальное соотношение величин, лежащее в основе гармонии природы и человека. «Золотое сечение» имеет массу удивительных свойств (из разряда «Ух, ты! Занимательная геометрия»), возможно, именно поэтому, ему приписывается некое божественное происхождение и ряд вымышленных свойств.

Если выражаться сухо по-научному, то ЗС — это соотношение величин или отрезков, при котором отношение большей части к меньшей равно отношению всей величины к большей части. Приблизительное округленное процентное соотношение частей — 62% и 38%.

Числовая величина золотого сечения – 1, 6180339887 (и это еще округление =)) до десятого знака!)

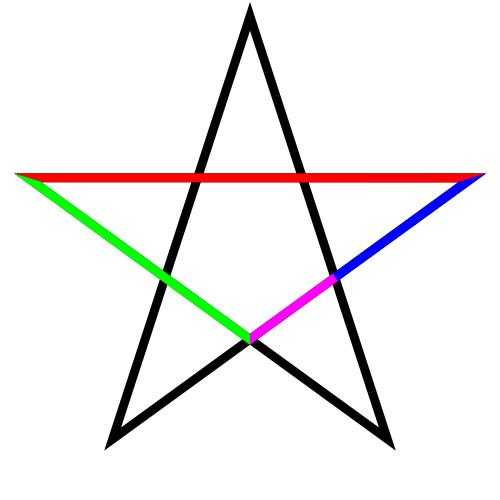
Пример золотого сечения в лучах пятиконечной звезды.

С Вашего позволения, я опущу многострочные математические фомулы и фомулировки =) Перейдем сразу к Прекрасному!

Зачатки этого понятия встречаются еще в античной литературе, датированной 300 гг. до нашей эры, а «божественная пропорция» широко применялась в трудах и работах мастеров Эпохи Возрождения. Иоган Кеплер, астроном 16 в. назвал золотое сечение одним из сокровищ геометрии. Он впервые обращает внимание то, как проявляется ЗС в ботанике (рост растений и строение стеблей и соцветий).

В середине 19 в. немецкий исследователь золотого сечения профессор Цейзинг опубликовал свой труд «Эстетические исследования». Цейзинг проделал колоссальную работу. Он измерил около двух тысяч человеческих тел и пришел к выводу, что золотое сечение лежит в основе некой среднестатистической пропорции человеческого тела. Деление тела точкой пупка – важнейший показатель золотого сечения. Пропорции мужского тела колеблются в пределах среднего отношения 13 к 8 = 1,625 и несколько ближе подходят к ЗС, чем пропорции женского тела, в отношении которого среднее значение пропорции выражается в соотношении 8 к 5 = 1,6. Пропорции золотого сечения проявляются и в отношении всех частей тела – длина плеча, предплечья и кисти, кисти и пальцев и т.д.

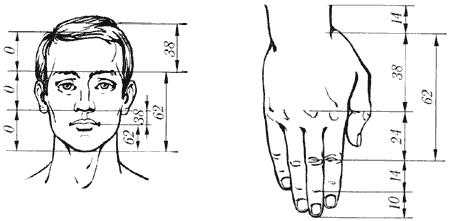
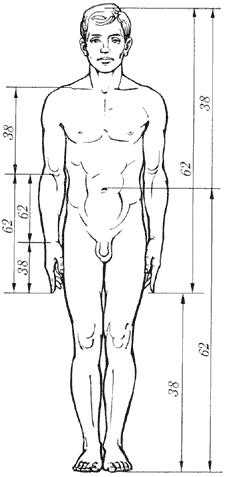
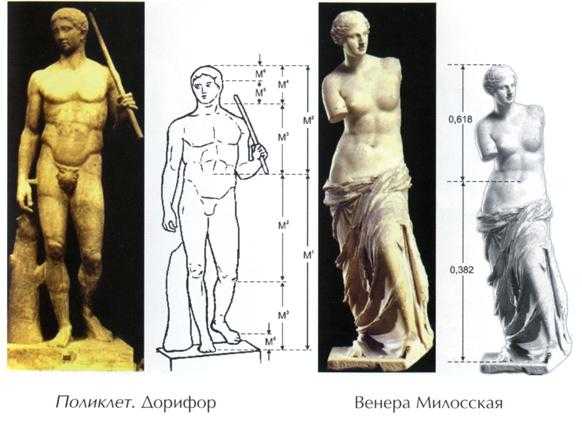
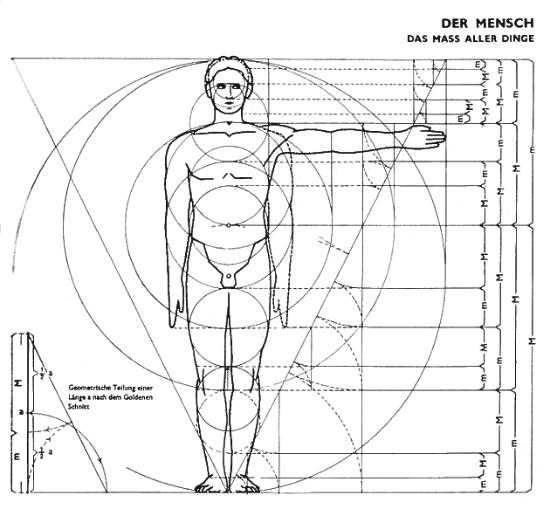
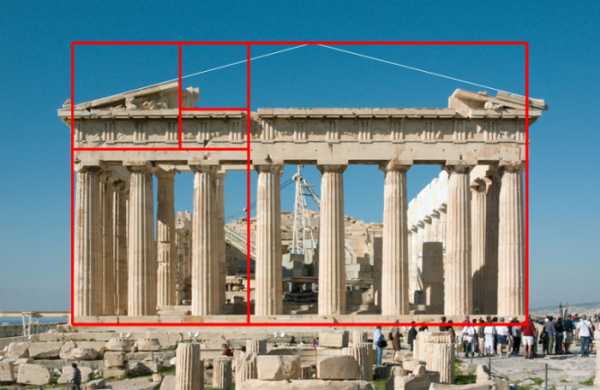
На протяжении веков существовало общеприянтое мнение, что рукотворные объекты, созданные с применением принципа ЗС, воспринимаются Человеком как наиболее гармоничные, совершенные. Пропорции золотого сечения можно выделить в проекциях египетских пирамид. Соотношение сторон плана Парфенона в Афинском Акрополе также являет собой не простое кратное число, а бесконечно дробное (догадайтесь, какое?). Таковыми же являются соотношение сторон планов и фасадов многих византийских церквей, романских готических соборов. Принято считать, что еще со времен Ренессанса многие художники и архитекторы сознательно используют принципы золотого сечения в своих творениях.

Золотое сечение на примере фасада храма Парфенона

Однако же, бытует и мнение, что значение ЗС в искусстве сильно преувеличенно, порой притянуто за уши исследователями, либо основано наошибочных расчетах. Тут каждый останется при своем. Помню, как на втором курсе в архитектурном нас, лопоухих, профессора пытались приобщить к прекрасному и долго-долго втолковывали про принципы золотого сечения в зодчестве, ряды Фибоначчи и прочее-прочее =)) Но настоящее понимание этой волшебной геометрии пришло ко мне много позже, при изучении бионики (один из стилей архитектуры), которая базируется именно на совершенстве природных форм. Согласитесь, мы не в силах оспаривать очевидное, а примеры идеальной пропорции встречаются сплошь и рядом: в раковинах аммонитов, в расположении ветвей на стебле растения, прожилках листьев. Ведь все, что приобретало какую-то форму, образовывалось, росло, осуществляло свое развитие в основном в двух вариантах – рост вверх или расстилание по поверхности земли и закручивание по спирали. Раковина закручена по спирали. И вообще, представление о золотом сечении будет неполным, если не сказать о спирали. Форма спирально завитой раковины привлекла внимание Архимеда. Он изучал ее и вывел уравнение спирали: увеличение ее шага всегда равномерно.

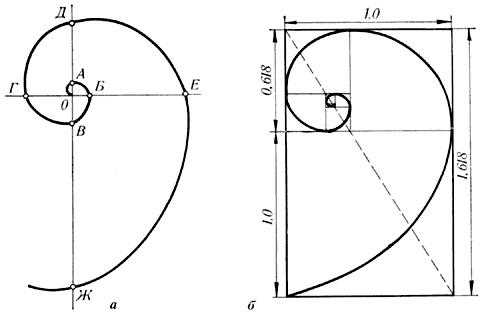
Спираль Архимеда

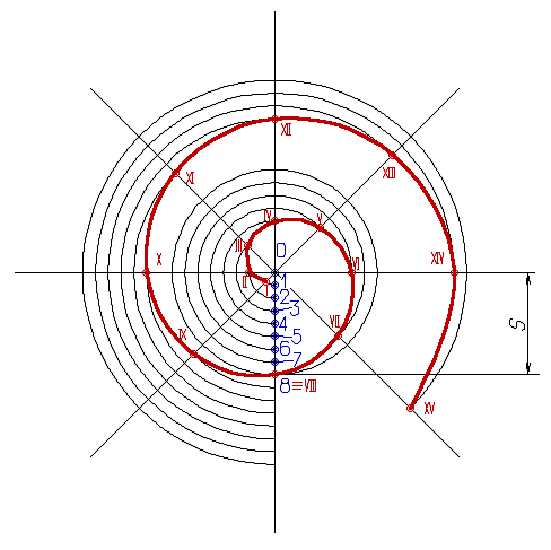
Винтообразное и спиралевидное расположение листьев на ветках деревьев подметили давно. Спираль увидели в расположении семян подсолнечника, в шишках сосны, ананасах, кактусах и т.д. Совместная работа ботаников и математиков пролила свет на эти удивительные явления природы. Выяснилось, что в расположении листьев на ветке , семян подсолнечника, шишек сосны проявляет себя закон золотого сечения. Паук плетет паутину спиралеобразно. Спиралью закручивается ураган. Испуганное стадо северных оленей разбегается по спирали. Молекула ДНК закручена двойной спиралью. Гете называл спираль «кривой жизни».

Стебель цикория

Полюбуйтесь, как наглябно иллюстрирует природа принципы Золотого сечения! Совершенные спирали без изъян, соотношения витков которых строго соответсвует канонам и принципам построения ЗС.

© Copyright: Tihomir Balkonskiy

© Copyright: Kibardindesign

Материалы взяты из Интернета.

Текст преимущественно авторский =)

Спасибо за Ваше внимание, Даша Самаркина

www.livemaster.ru

Золотое сечение

Любому человеку, которому хотя бы косвенно приходилось сталкиваться с геометрией пространственных объектов в интерьерном дизайне и архитектуре, наверняка хорошо известен принцип золотого сечения. Еще недавно, несколько десятков лет назад, популярность золотого сечения была настолько высокой, что многочисленные сторонники мистических теорий и устройства мира его называют универсальным гармоническим правилом.

Сущность универсальной пропорции

Удивительно другое. Причиной предвзятого, почти мистического отношения к столь простой числовой зависимости послужило несколько необычных свойств:

• Большое количество объектов живого мира, от вируса до человека, имеют основные пропорции тела или конечностей, очень близкие к значению золотого сечения;
• Зависимость 0,63 или 1,62 характерна только для биологических существ и некоторых разновидностей кристаллов, неживые объекты, от минералов до элементов ландшафта, обладают геометрией золотого сечения крайне редко;
• Золотые пропорции в строении тела оказались наиболее оптимальными для выживания реальных биологических объектов.

Сегодня золотое сечение находят в строении тела животных, панцирей и раковин моллюсков, пропорций листьев, веток, стволов и корневых систем у достаточно большого числа кустарников и трав.

Многими последователями теории универсальности золотого сечения неоднократно предпринимались попытки доказать тот факт, что его пропорции являются наиболее оптимальными для биологических организмов в условиях их существования.

Обычно в качестве примера приводится устройство раковины Astreae Heliotropium, одного из морских моллюсков. Панцирь представляет собой свернутую спиралью кальцитовую оболочку с геометрией, практически совпадающей с пропорциями золотого сечения.

Более понятным и очевидным примером является обычное куриное яйцо.

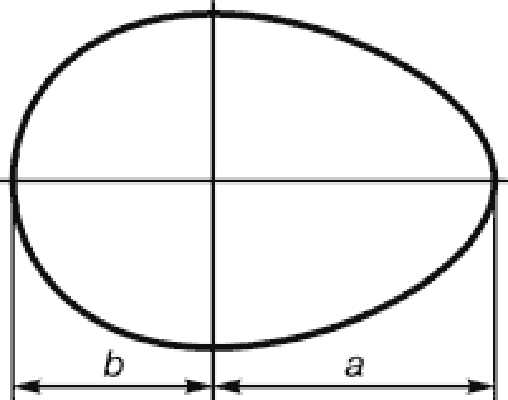
Соотношение основных параметров, а именно, большого и малого фокуса, или расстояний от равноудаленных точек поверхности до центра тяжести, будет также соответствовать золотому сечению. При этом форма скорлупы птичьего яйца является наиболее оптимальной для выживания птицы, как биологического вида. При этом прочность скорлупы играет далеко не главную роль.

Происхождение универсальной пропорции

О золотой пропорции сечения знали древнегреческие математики Евклид и Пифагор. В одном из памятников древней архитектуры — пирамиде Хеопса соотношение сторон и основания, отдельные элементы и настенные барельефы выполнены в соответствии с универсальной пропорцией.

Методика золотого сечения широко использовалась в средние века художниками и архитекторами, при этом суть универсальной пропорции считалась одной из тайн вселенной и тщательно скрывалась от простого обывателя. Композиция многих картин, скульптур и зданий выстраивалась строго в соответствии с пропорциями золотого сечения.

Впервые суть универсальной пропорции документально была сформулирована в 1509 г монахом-францисканцем Лукой Пачоли, обладавшим блестящими математическими способностями. Но настоящее признание состоялось после проведения немецким ученым Цейзингом всестороннего изучения пропорций и геометрии человеческого тела, древних скульптур, произведений искусства, животных и растений.

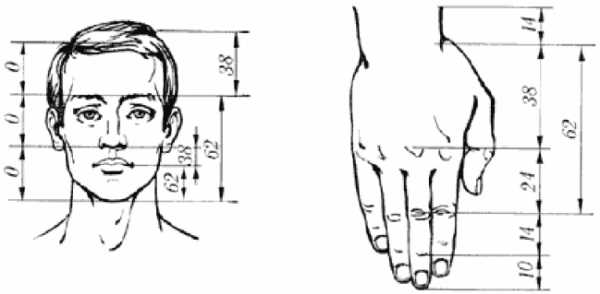
У большинства живых объектов некоторые размеры тела подчиняются одним и тем же пропорциям. В 1855 г ученым был сделан вывод о том, что пропорции золотого сечения являются своеобразным стандартом гармонии тела и формы. Речь идет, прежде всего, о живых существах, для мертвой природы золотое сечение встречается значительно реже.

Как получили золотое сечение

Пропорцию золотого сечения проще всего представить, как отношение двух частей одного объекта разной длины, разделенных точкой.

Проще говоря, сколько длин маленького отрезка поместится внутри большого, или отношение самой большей из частей ко всей длине линейного объекта. В первом случае соотношение золотого сечения составляет 0,63, во втором варианте соотношение сторон равняется 1,618034.

На практике золотое сечение представляет собой всего лишь пропорцию, соотношение отрезков определенной длины, сторон прямоугольника или других геометрических форм, родственных или сопряженных размерных характеристик реальных объектов.

Первоначально золотые пропорции были выведены эмпирическим путем с помощью геометрических построений. Существует несколько способов построения или выведения гармонической пропорции:

• Классическим разбиением одной из сторон прямоугольного треугольника и построением перпендикуляров и секущих дуг. Для этого из одного конца отрезка необходимо восстановить перпендикуляр высотой в ½ его длины и построить прямоугольный треугольник, как на схеме.
  
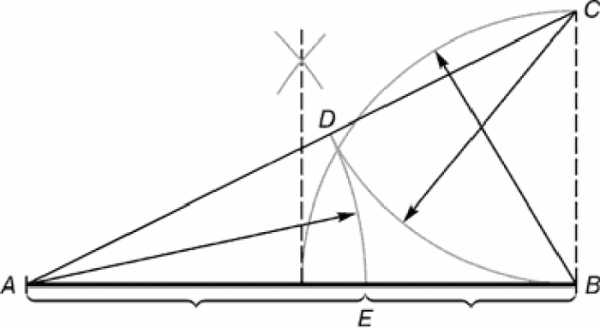
  Если на гипотенузе отложить высоту перпендикуляра, то радиусом, равным оставшемуся отрезку, основание рассекается на два отрезка с длинами, пропорциональными золотому сечению;
• Методом построения пентаграммы Дюрера, гениального немецкого графика и геометра. Сегодня мы знаем метод золотого сечения Дюрера, как способ построения звезды или пентаграммы, вписанной в окружность, в которой как минимум четыре отрезка гармоничной пропорции;
• В архитектуре и строительстве золотое сечение чаще используется в усовершенствованном виде. В этом случае используется разбиение прямоугольного треугольника не по катету, а по гипотенузе, как схеме.

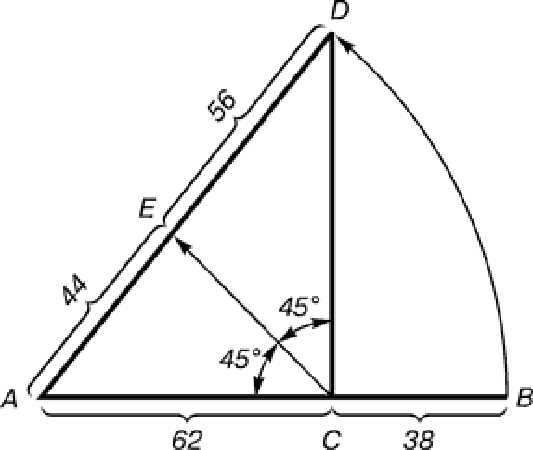
Если стандартный вариант золотого сечения для живых существ, живописи, графики, скульптур и античных построек рассчитывался, как 37:63, то золотое сечение в архитектуре с конца XVII века все чаще стало использоваться 44:56. Большинство специалистов считают изменение в пользу более «квадратных» пропорций распространением высотного строительства.

Главный секрет золотого сечения

Если природные проявления универсального сечения в пропорциях тел животных и человека, стеблевой основы растений еще можно объяснить эволюцией и приспосабливаемостью к влиянию внешней среды, то открытие золотого сечения в строительстве домов XII-XIX века стало определенной неожиданностью. Мало того, знаменитый древнегреческий Парфенон был построен с соблюдением универсальной пропорции, многие дома и замки состоятельных вельмож и зажиточных людей в средние века строились сознательно с параметрами, очень близкими к золотому сечению.

Золотое сечение в архитектуре

Многие из построек, сохранившихся до сегодняшних дней, свидетельствуют, что архитекторы средневековья знали о существовании золотого сечения, и, конечно, при строительстве дома руководствовались своими примитивными расчетами и зависимостями, с помощью которых пытались добиться максимальной прочности. Особенно проявлялось желание строить максимально красивые и гармоничные дома в постройках резиденций царствующих особ, церквей, ратуш и зданий, имеющих особое социальное значение в обществе.

Например, знаменитый собор Парижской богоматери в своих пропорциях имеет немало участков и размерных цепей, соответствующих золотому сечению.

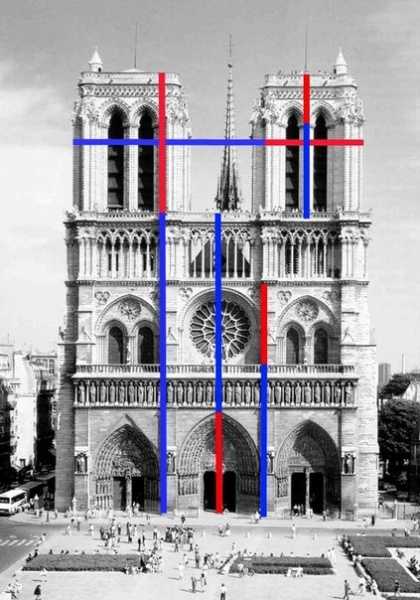
Еще до публикации своих исследований в 1855 году профессором Цейзингом, в конце XVIII века были построены знаменитые архитектурные комплексы Голицынской больницы и здания сената в Санкт-Петербурге, дома Пашкова и Петровского дворца в Москве с использованием пропорций золотого сечения.

Разумеется, дома с точным соблюдением правила золотого сечения строили и ранее. Стоит упомянуть памятник древней архитектуры церкви Покрова на Нерли, изображенный на схеме.

Всех их объединяет не только гармоничное сочетание форм и высокое качество строительства, но и, в первую очередь, наличие золотого сечения в пропорциях здания. Удивительная красота постройки становится еще более загадочной, если принять во внимание возраст, здание церкви Покрова датируется XIII веком, но современный архитектурный облик постройка получила на рубеже XVII века в результате реставрации и перестройки.

Особенность золотого сечения для человека

Старинная архитектура зданий и домов средневековья остается притягательной и интересной для современного человека по многим причинам:

• Индивидуальный художественный стиль в оформлении фасадов позволяет избежать современного штампа и серости, каждое здание представляет собой произведение искусства;
• Массовое использование для декорирования и украшения статуй, скульптур, лепнины, необычных сочетаний строительных решений разных эпох;
• Пропорции и композиции здания притягивают взор к наиболее важным элементам постройки.

Важно! При проектировании дома и разработке внешнего вида средневековые архитекторы применяли правило золотого сечения, неосознанно используя особенности восприятия подсознания человека.

Современные психологи экспериментально доказали, что золотое сечение является проявлением неосознанного желания или реакции человека на гармоничное сочетание или пропорцию в размерах, формах и даже цветах. Был проведен эксперимент, в ходе которого группе людей, незнакомых между собой, не имеющих общих интересов, разных профессий и возрастных категорий, предложили ряд тестов, среди которых была задача согнуть лист бумаги в наиболее оптимальной пропорции сторон. По результатам тестирования было установлено, что в 85 случаях из 100 лист сгибался испытуемыми практически точно по золотому сечению.

Поэтому современная наука считает, что феномен универсальной пропорции является психологическим явлением, а не действием каких-либо метафизических сил.

Использование фактора универсального сечения в современном дизайне и архитектуре

Принципы применения золотой пропорции в последние несколько лет стали необыкновенно популярны в строительстве частных домов. На смену экологии и безопасности строительных материалов пришли гармоничность конструкции и правильное распределение энергии внутри дома.

Современная интерпретация правила всеобщей гармонии давно распространилась за пределы привычной геометрии и формы объекта. Сегодня правилу подчиняются не только размерные цепи длины портика и фронтона, отдельных элементов фасада и высоты здания, но и площадь комнат, оконных и дверных проемов, и даже цветовая гамма внутреннего интерьера помещения.

Проще всего построить гармоничный дом на модульной основе. В этом случае большинство отделений и комнат изготавливаются в виде самостоятельных блоков или модулей, спроектированных с соблюдением правила золотого сечения. Построить здание в виде набора гармоничных модулей значительно проще, чем строить одну коробку, в которой большая часть фасада и внутренних помещений должна быть в жестких рамках пропорций золотого сечения.

Немало строительных фирм, выполняющих проектирование частных домовладений, используют принципы и понятия золотого сечения для увеличения сметы и создания у клиентов впечатления глубокой проработки конструкции дома. Как правило, такой дом декларируется, как очень удобный и гармоничный в пользовании. Правильно подобранное соотношение площадей комнат гарантирует душевный комфорт и отменное здоровье хозяев.

Если дом был построен без учета оптимальных соотношений золотого сечения, можно выполнить перепланировку комнат так, чтобы пропорции помещения соответствовали соотношению стен в пропорции 1:1,61. Для этого может перемещаться мебель или устанавливаться дополнительные перегородки внутри комнат. Аналогичным образом меняются размеры оконных и дверных проемов так, чтобы ширина проема была меньше высоты дверного полотна в 1,61 раза. Таким же способом выполняется планирование мебели, бытовой техники, отделки стен и пола.

Сложнее выбрать цветовое оформление. В этом случае вместо привычного соотношения 63:37 последователями золотого правила принята упрощенная трактовка – 2/3. То есть основной цветовой фон должен занимать 60% пространства помещения, оттеняющему цвету отдают не более 30%, и остальное отводится под различные родственные тона, призванные усилить восприятие цветового решения.

Внутренние стены помещения делятся горизонтальным поясом или бордюром на высоте 70 см, установленная мебель должна соизмеряться с высотой потолков по соотношению золотого сечения. То же правило касается распределения длин, например, размер дивана не должен превышать 2/3 длины простенка, а общая площадь, занимаемая мебелью, относится к площади комнаты, как 1:1,61.

Золотую пропорцию сложно в массовом порядке применять на практике из-за всего лишь одного значения сечения, поэтому при проектировании гармоничных зданий нередко прибегают к ряду чисел Фибоначчи. Это позволяет расширить количество возможных вариантов пропорций и геометрических форм основных элементов дома. В этом случае ряд чисел Фибоначчи, связанных между собой четкой математической зависимостью, называют гармоническим или золотым.

В современной методике проектирования жилья на основе принципа золотого сечения, кроме ряда Фибоначчи, широко используется принцип, предложенный известным французским архитектором Ле Корбюзье. В этом случае в качестве отправной единицы измерения, по которой рассчитываются все параметры здания и внутреннего интерьера, выбирается рост будущего владельца или средняя высота человека. Такой подход позволяет спроектировать дом не только гармоничный, но и по-настоящему индивидуальный.

Заключение

На практике, по отзывам тех, кто решился на строительство дома по правилу золотого сечения, качественно построенное здание действительно оказывается достаточно удобным для проживания. Но стоимость строения из-за индивидуального проектирования и применения стройматериалов нестандартных размеров возрастает на 60-70%. И в этом подходе нет ничего нового, так как большинство зданий прошлого века строилось именно под индивидуальные особенности будущих хозяев.

bouw.ru

🍀 Божественная гармония: что такое золотое сечение: пропорции и принципы

Эта гармония поражает своими масштабами…

Здравствуйте, друзья!

Вы что-нибудь слышали о Божественной гармонии или Золотом сечении? Задумывались ли о том, почему нам что-то кажется идеальным и красивым, а что-то отталкивает?

Если нет, то вы удачно попали на эту статью, потому что в ней мы обсудим золотое сечение, узнаем что это такое, как оно выглядит в природе и в человеке. Поговорим о его принципах, узнаем что такое ряд Фибоначчи и многое многое другое, включая понятие золотой прямоугольник и золотая спираль.

Да, в статье много изображений, формул, как-никак, золотое сечение — это еще и математика. Но все описано достаточно простым языком, наглядно. А еще, в конце статьи, вы узнаете, почему все так любят котиков =)

Что такое золотое сечение?

Если по-простому, то золотое сечение — это определенное правило пропорции, которое создает гармонию?. То есть, если мы не нарушаем правила этих пропорций, то у нас получается очень гармоничная композиция.

Наиболее емкое определение золотого сечения гласит, что меньшая часть относится к большей, как большая ко всему целому.

Но, кроме этого, золотое сечение — это математика: у него есть конкретная формула и конкретное число. Многие математики, вообще, считают его формулой божественной гармонии, и называют «асимметричной симметрией».

До наших современников золотое сечение дошло со времен Древней Греции, однако, бытует мнение, что сами греки уже подсмотрели золотое сечение у египтян. Потому что многие произведения искусства Древнего Египта четко построены по канонам этой пропорции.

Золотое сечение в математике

Считается, что первым ввел понятие золотого сечения Пифагор. До наших дней дошли труды Евклида (он при помощи золотого сечения строил правильные пятиугольники, именно поэтому такой пятиугольник назван «золотым»), а число золотого сечения названо в честь древнегреческого архитектора Фидия. То есть, это у нас число «фи» (обозначается греческой буквой φ), и равно оно 1.6180339887498948482… Естественно, это значение округляют: φ = 1,618 или φ = 1,62, а в процентном соотношении золотое сечение выглядит, как 62% и 38%.

В чем же уникальность этой пропорции (а она, поверьте, есть)? Давайте для начала попробуем разобраться на примере отрезка. Итак, берем отрезок и делим его на неравные части таким образом, чтобы его меньшая часть относилась к большей, как большая ко всему целому. Понимаю, не очень пока ясно, что к чему, попробую проиллюстрировать наглядней на примере отрезков:

Итак, берем отрезок и делим его на два других, таким образом, чтобы меньший отрезок а, относился к большему отрезку b, так же, как и отрезок b относится к целому, то есть ко всей линии (a + b). Математически это выглядит так:

Этот правило работает бесконечно, вы можете делить отрезки сколь угодно долго. И, видите, как это просто. Главное один раз понять и все.

Но теперь рассмотрим более сложный пример, который попадается очень часто, так как золотое сечение еще представляют в виде золотого прямоугольника (соотношение сторон которого равно φ = 1,62). Это очень интересный прямоугольник: если от него «отрезать» квадрат, то мы снова получим золотой прямоугольник. И так бесконечно много раз. Смотрите:

Но математика не была бы математикой, если бы в ней не было формул. Так что, друзья, сейчас будет немножко «больно». Решение золотой пропорции спрятала под спойлер, очень много формул, но без них не хочу оставлять статью.

Ряд Фибоначчи и золотое сечение

Продолжаем творить и наблюдать за магией математики и золотого сечения. В средние века был такой товарищ — Фибоначчи (или Фибоначи, везде по-разному пишут). Любил математику и задачи, была у него и интересная задачка с размножением кроликов =) Но не в этом суть. Он открыл числовую последовательность, числа в ней так и зовутся «числа Фибоначчи».

Сама последовательность выглядит так:

0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233… и дальше до бесконечности.

Если словами, то последовательность Фибоначчи — это такая последовательность чисел, где каждое последующее число, равно сумме двух предыдущих.

Причем здесь золотое сечение? Сейчас увидите.

Спираль Фибоначчи

Чтобы увидеть и прочувствовать всю связь числового ряда Фибоначчи и золотого сечения, нужно снова взглянуть на формулы.

Иными словами, с 9-го члена последовательности Фибоначчи мы начинаем получать значения золотого сечения. И если визуализировать всю эту картину, то мы увидим, как последовательность Фибоначчи создает прямоугольники все ближе и ближе к золотому прямоугольнику. Вот такая вот связь.

Теперь поговорим о спирали Фибоначчи, ее еще называют «золотой спиралью».

Золотая спираль — логарифмическая спираль, коэффициент роста которой равен φ4, где φ — золотое сечение.

В общем и целом, с точки зрения математики, золотое сечение — идеальная пропорция. Но на этом ее чудеса только начинаются. Принципам золотого сечения подчинен почти весь мир, эту пропорцию создала сама природа. Даже эзотерики, и те, видят в ней числовую мощь. Но об этом точно не в этой статье будем говорить, поэтому, чтобы ничего не пропустить, можете подписаться на обновления сайта.

Золотое сечение в природе, человеке, искусстве

Прежде, чем мы начнем, хотелось бы уточнить ряд неточностей. Во-первых, само определение золотого сечения в данном контексте не совсем верно. Дело в том, что само понятие «сечение» — это термин геометрический, обозначающий всегда плоскость, но никак не последовательность чисел Фибоначчи.

И, во-вторых, числовой ряд и соотношение одного к другому, конечно, превратили в некий трафарет, который можно накладывать на все, что кажется подозрительным, и очень радоваться, когда есть совпадения, но все же, здравый смысл терять не стоит.

Однако, «все смешалось в нашем королевстве» и одно стало синонимом другого. Так что в общем и целом, смысл от этого не потерялся. А теперь к делу.

Вы удивитесь, но золотое сечение, точнее пропорции максимально приближенные к нему, можно увидеть практически везде, даже в зеркале. Не верите? Давайте с этого и начнем.

Пропорции золотого сечения в человеке

Знаете, когда я училась рисовать, то нам объясняли, как проще строить лицо человека, его тело и прочее. Все надо рассчитывать, относительно чего-то другого.

Все, абсолютно все пропорционально: кости, наши пальцы, ладони, расстояния на лице, расстояние вытянутых рук по отношению к телу и так далее. Но даже это не все, внутреннее строение нашего организма, даже оно, приравнивается или почти приравнивается к золотой формуле сечения. Вот какие расстояния и пропорции:

• от плеч до макушки к размеру головы = 1:1.618

• от пупка до макушки к отрезку от плеч до макушки = 1:1.618

• от пупка до коленок и от коленок до ступней = 1:1.618

• от подбородка до крайней точки верхней губы и от нее до носа = 1:1.618

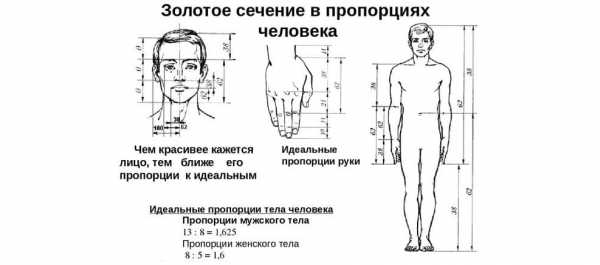
Разве это не удивительно!? Гармония в чистом виде, как внутри, так и снаружи. И именно поэтому, на каком-то подсознательном что-ли уровне, некоторые люди не кажутся нам красивыми, даже если у них крепкое подтянутое тело, бархатная кожа, красивые волосы, глаза и прочее и все остальное. Но, все равно, малейшее нарушений пропорций тела, и внешность уже слегка «режет глаза».

Короче говоря, чем красивее кажется нам человек, тем ближе его пропорции к идеальным. И это, кстати, не только к человеческому телу можно отнести.

Золотое сечение в природе и ее явлениях

Классическим примером золотого сечения в природе является раковина моллюска Nautilus pompilius и аммонита. Но это далеко не все, есть еще много примеров:

• в завитках человеческого уха мы можем увидеть золотую спираль;

• ее же (или приближенную к ней) в спиралях, по которым закручиваются галактики;

• и в молекуле ДНК;

• по ряду Фибоначчи устроен центр подсолнуха, растут шишки, середина цветов, ананас и многие другие плоды.

Друзья, примеров настолько много, что я просто оставлю тут видеоролик (он чуть ниже), чтобы не перегружать текстом статью. Потому что, если эту тему копать, то можно углубиться в такие дебри: еще древние греки доказывали, что Вселенная и, вообще, все пространство, — спланировано по принципу золотого сечения.

Вы удивитесь, но эти правила можно отыскать даже в звуке. Смотрите:

• Наивысшая точка звука, вызывающая боль и дискомфорт в наших ушах, равна 130 децибелам.

• Делим пропорцией 130 на число золотого сечения φ = 1,62 и получаем 80 децибел — звук человеческого крика.

• Продолжаем пропорционально делить и получаем, скажем так, нормальную громкость человеческой речи: 80 / φ = 50 децибел.

• Ну, а последний звук, который получим благодаря формуле – приятный звук шепота = 2,618.

По данному принципу можно определить оптимально-комфортное, минимальное и максимальное число температуры, давления, влажности. Я не проверяла, и не знаю, насколько эта теория верна, но, согласитесь, звучит впечатляюще.

Абсолютно во всем живом и не живом можно прочесть высшую красоту и гармонию.

Главное, только не увлекаться этим, ведь если мы хотим что-то в чем-то увидеть, то увидим, даже если этого там нет. Вот я, например, обратила внимание на дизайн PS4 и увидела там золотое сечение =) Впрочем, эта консоль настолько классная, что не удивлюсь, если дизайнер, и правда, что-то там мудрил.

Золотое сечение в искусстве

Тоже очень большая и обширная тема, которую стоит рассмотреть отдельно. Тут лишь помечу несколько базовых моментов. Самое примечательное, что многие произведения искусства и архитектурные шедевры древности (и не только) сделаны, по принципам золотого сечения.

• Египетские и пирамиды Майя, Нотр-дам де Пари, греческий Парфенон и так далее.

• В музыкальных произведениях Моцарта, Шопена, Шуберта, Баха и прочих.

• В живописи (там это наглядно видно): все самые знаменитые картины известных художников сделаны с учетом правил золотого сечения.

• Эти принципы можно встретить и в стихах Пушкина, и в бюсте красавицы Нефертити.

• Даже сейчас правила золотой пропорции используются, например, в фотографии. Ну, и конечно, во всем остальном искусстве, включая кинематограф и дизайн.

Золотые котики Фибоначчи

Ну и, наконец, о котиках! Вы задумывались о том, почему все так любят котеек? Они же ведь заполонили Интернет! Котики везде и это чудесно =)

А все дело в том, что кошки — идеальны! Не верите? Сейчас докажу вам это математически!

Видите? Тайна раскрыта! Котейки идеальны с точки зрения математики, природы и Вселенной =)

* Я шучу, конечно. Нет, кошки, действительно, идеальны) Но математически их никто не измерял, наверное.

На этом, в общем-то, все, друзья! Мы увидимся в следующих статьях. Удачи вам!

P. S. Изображения взяты с сайта medium.com.

pearative.ru

Золотое сечение: как это работает

Золотое сечение — это универсальное проявление структурной гармонии. Оно встречается в природе, науке, искусстве – во всем, с чем может соприкоснуться человек. Однажды познакомившись с золотым правилом, человечество больше ему не изменяло.

Определение

Наиболее емкое определение золотого сечения гласит, что меньшая часть относится к большей, как большая ко всему целому. Приблизительная его величина – 1,6180339887. В округленном процентном значении пропорции частей целого будут соотноситься как 62% на 38%. Это соотношение действует в формах пространства и времени. Древние видели в золотом сечении отражение космического порядка, а Иоганн Кеплер называл его одним из сокровищ геометрии. Современная наука рассматривает золотое сечение как «ассиметричную симметрию», называя его в широком смысле универсальным правилом отражающим структуру и порядок нашего мироустройства.

История

Принято считать, что понятие о золотом делении ввёл в научный обиход Пифагор, древнегреческий философ и математик (VI в. до н.э.). Есть предположение, что Пифагор своё знание золотого деления позаимствовал у египтян и вавилонян. И действительно, пропорции пирамиды Хеопса, храмов, барельефов, предметов быта и украшений из гробницы Тутанхамона свидетельствуют, что египетские мастера пользовались соотношениями золотого деления при их создании. Французский архитектор Ле Корбюзьенашёл, что в рельефе из храма фараона Сети I в Абидосе и в рельефе, изображающем фараона Рамзеса, пропорции фигур соответствуют величинам золотого деления. Зодчий Хесира, изображённый на рельефе деревянной доски из гробницы его имени, держит в руках измерительные инструменты, в которых зафиксированы пропорции золотого деления.

Греки были искусными геометрами. Даже арифметике обучали своих детей при помощи геометрических фигур. Квадрат Пифагора и диагональ этого квадрата были основанием для построения динамических прямоугольников.

Платон (427…347 гг. до н.э.) также знал о золотом делении. Его диалог «Тимей» посвящён математическим и эстетическим воззрениям школы Пифагора и, в частности, вопросам золотого деления.

В фасаде древнегреческого храма Парфенона присутствуют золотые пропорции. При его раскопках обнаружены циркули, которыми пользовались архитекторы и скульпторы античного мира. В Помпейском циркуле (музей в Неаполе) также заложены пропорции золотого деления.

     Рис.  Античный циркуль золотого сечения

В дошедшей до нас античной литературе золотое деление впервые упоминается в «Началах» Евклида. Во 2-й книге «Начал» даётся геометрическое построение золотого деления. После Евклида исследованием золотого деления занимались Гипсикл (II в. до н.э.), Папп (III в. н.э.) и др. В средневековой Европе с золотым делением познакомились по арабским переводам «Начал» Евклида. Переводчик Дж. Кампано из Наварры (III в.) сделал к переводу комментарии. Секреты золотого деления ревностно оберегались, хранились в строгой тайне. Они были известны только посвящённым.

Представление о золотых пропорциях имели и на Руси, но впервые научно золотое сечение объяснил монах Лука Пачоли в книге «Божественная пропорция» (1509), иллюстрации к которой предположительно сделал Леонардо да Винчи. Пачоли усматривал в золотом сечении божественное триединство: малый отрезок олицетворял Сына, большой – Отца, а целое – Святой дух. По мнению современников и историков науки, Лука Пачоли был настоящим светилом, величайшим математиком Италии в период между Фибоначчи и Галилеем. Лука Пачоли был учеником художника Пьеро делла Франчески, написавшего две книги, одна из которых называлась «О перспективе в живописи». Его считают творцом начертательной геометрии.

Лука Пачоли прекрасно понимал значение науки для искусства. В 1496 г. по приглашению герцога Моро он приезжает в Милан, где читает лекции по математике. В Милане при дворе Моро в то время работал и Леонардо да Винчи. 

Непосредственным образом с правилом золотого сечения связано имя итальянского математика Леонардо Фибоначчи. В результате решения одной из задач ученый вышел на последовательность чисел, известную сейчас как ряд Фибоначчи: 1, 2, 3, 5, 8, 13, 21, 34, 55 и т.д. На отношение этой последовательности к золотой пропорции обратил внимание Кеплер: «Устроена она так, что два младших члена этой нескончаемой пропорции в сумме дают третий член, а любые два последних члена, если их сложить, дают следующий член, причем та же пропорция сохраняется до бесконечности». Сейчас ряд Фибоначчи это арифметическая основа для расчетов пропорций золотого сечения во всех его проявлениях.

Леонардо да Винчи также много времени посвятил изучению особенностей золотого сечения, скорее всего именно ему принадлежит и сам термин. Его рисунки стереометрического тела, образованного правильными пятиугольниками, доказывают, что каждый из полученных при сечении прямоугольников дает соотношения сторон в золотом делении.

Со временем правило золотого сечения превратилось в академическую рутину, и только философ Адольф Цейзинг в 1855 году вернул ему вторую жизнь. Он довел до абсолюта пропорции золотого сечения, сделав их универсальными для всех явлений окружающего мира. Впрочем, его «математическое эстетство» вызывало много критики.

Природа

Астроном XVI в. Иоганн Кеплер назвал золотое сечение одним из сокровищ геометрии. Он первый обращает внимание на значение золотой пропорции для ботаники (рост растений и их строение).

Кеплер называл золотую пропорцию продолжающей саму себя «Устроена она так, – писал он, – что два младших члена этой нескончаемой пропорции в сумме дают третий член, а любые два последних члена, если их сложить, дают следующий член, причём та же пропорция сохраняется до бесконечности».

Построение ряда отрезков золотой пропорции можно производить как в сторону увеличения (возрастающий ряд), так и в сторону уменьшения (нисходящий ряд).

Если на прямой произвольной длины, отложить отрезок m, рядом откладываем отрезок M. На основании этих двух отрезков выстраиваем шкалу отрезков золотой пропорции восходящего и нисходящего рядов.

    Рис. Построение шкалы отрезков золотой пропорции

     Рис. Цикорий

Даже не вдаваясь в расчеты, золотое сечение можно без труда обнаружить в природе. Так, под него попадают соотношение хвоста и тела ящерицы, расстояния между листьями на ветке, есть золотое сечение и в форме яйца, если условную линию провести через его наиболее широкую часть.

     Рис. Ящерица живородящая

     Рис. Яйцо птицы

Белорусский ученый Эдуард Сороко, который изучал формы золотых делений в природе, отмечал, что все растущее и стремящееся занять свое место в пространстве, наделено пропорциями золотого сечения. По его мнению, одна из самых интересных форм это закручивание по спирали.

Еще Архимед, уделяя внимание спирали, вывел на основе ее формы уравнение, которое и сейчас применяется в технике. Позднее Гёте отмечал тяготение природы к спиральным формам, называя спираль «кривой жизни». Современными учеными было установлено, что такие проявления спиральных форм в природе как раковина улитки, расположение семян подсолнечника, узоры паутины, движение урагана, строение ДНК и даже структура галактик заключают в себе ряд Фибоначчи.

Человек

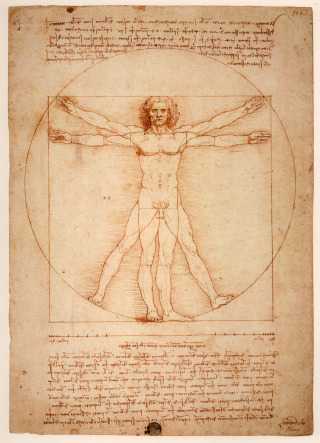
Модельеры и дизайнеры одежды все расчеты делают, исходя из пропорций золотого сечения. Человек – это универсальная форма для проверки законов золотого сечения. Конечно, от природы далеко не у всех людей пропорции идеальны, что создает определенные сложности с подбором одежды.

В дневнике Леонардо да Винчи есть рисунок вписанного в окружность обнаженного человека, находящегося в двух наложенных друг на друга позициях. Опираясь на исследования римского архитектора Витрувия, Леонардо подобным образом пытался установить пропорции человеческого тела. Позднее французский архитектор Ле Корбюзье, используя «Витрувианского человека» Леонардо, создал собственную шкалу «гармонических пропорций», повлиявшую на эстетику архитектуры XX века. Адольф Цейзинг, исследуя пропорциональность человека, проделал колоссальную работу. Он измерил порядка двух тысяч человеческих тел, а также множество античных статуй и вывел, что золотое сечение выражает среднестатистический закон. В человеке ему подчинены практически все части тела, но главный показатель золотого сечения это деление тела точкой пупа.

В результате измерений исследователь установил, что пропорции мужского тела 13:8 ближе к золотому сечению, чем пропорции женского тела – 8:5.

Искусство пространственных форм

Художник Василий Суриков говорил, «что в композиции есть непреложный закон, когда в картине нельзя ничего ни убрать, ни добавить, даже лишнюю точку поставить нельзя, это настоящая математика». Долгое время художники следователи этому закону интуитивно, но после Леонардо да Винчи процесс создания живописного полотна уже не обходится без решения геометрических задач. Например, Альбрехт Дюрер для определения точек золотого сечения использовал изобретенный им пропорциональный циркуль.

Искусствовед Ф. В. Ковалев, подробно исследовав картину Николая Ге «Александр Сергеевич Пушкин в селе Михайловском», отмечает, что каждая деталь полотна будь-то камин, этажерка, кресло или сам поэт строго вписаны в золотые пропорции. Исследователи золотого сечения без устали изучают и замеряют шедевры архитектуры, утверждая, что они стали таковыми, потому что созданы по золотым канонам: в их списке Великие пирамиды Гизы, Собор Парижской Богоматери, Храм Василия Блаженного, Парфенон.

И сегодня в любом искусстве пространственных форм стараются следовать пропорциям золотого сечения, так как они, по мнению искусствоведов, облегчают восприятие произведения и формируют у зрителя эстетическое ощущение.

Гёте, поэт, естествоиспытатель и художник (он рисовал и писал акварелью), мечтал о создании единого учения о форме, образовании и преобразовании органических тел. Это он ввёл в научный обиход термин морфология.

Пьер Кюри в начале нашего столетия сформулировал ряд глубоких идей симметрии. Он утверждал, что нельзя рассматривать симметрию какого-либо тела, не учитывая симметрию окружающей среды.

Закономерности «золотой» симметрии проявляются в энергетических переходах элементарных частиц, в строении некоторых химических соединений, в планетарных и космических системах, в генных структурах живых организмов. Эти закономерности, как указано выше, есть в строении отдельных органов человека и тела в целом, а также проявляются в биоритмах и функционировании головного мозга и зрительного восприятия.

Золотое сечение и симметрия

Золотое сечение нельзя рассматривать само по себе, отдельно, без связи с симметрией. Великий русский кристаллограф Г.В. Вульф (1863…1925) считал золотое сечение одним из проявлений симметрии.

Золотое деление не есть проявление асимметрии, чего-то противоположного симметрии. Согласно современным представлениям золотое деление – это асимметричная симметрия. В науку о симметрии вошли такие понятия, как статическая и динамическая симметрия. Статическая симметрия характеризует покой, равновесие, а динамическая – движение, рост. Так, в природе статическая симметрия представлена строением кристаллов, а в искусстве характеризует покой, равновесие и неподвижность. Динамическая симметрия выражает активность, характеризует движение, развитие, ритм, она – свидетельство жизни. Статической симметрии свойственны равные отрезки, равные величины. Динамической симметрии свойственно увеличение отрезков или их уменьшение, и оно выражается в величинах золотого сечения возрастающего или убывающего ряда.

Слово, звук и кинолента

Формы временно̀го искусства по-своему демонстрируют нам принцип золотого деления. Литературоведы, к примеру, обратили внимание, что наиболее популярное количество строк в стихотворениях позднего периода творчества Пушкина соответствует ряду Фибоначчи – 5, 8, 13, 21, 34.

Действует правило золотого сечения и в отдельно взятых произведениях русского классика. Так кульминационным моментом «Пиковой дамы» является драматическая сцена Германа и графини, заканчивающаяся смертью последней. В повести 853 строки, а кульминация приходится на 535 строке (853:535=1,6) – это и есть точка золотого сечения.

Советский музыковед Э. К. Розенов отмечает поразительную точность соотношений золотого сечения в строгих и свободных формах произведений Иоганна Себастьяна Баха, что соответствует вдумчивому, сосредоточенному, технически выверенному стилю мастера. Это справедливо и в отношении выдающихся творений других композиторов, где на точку золотого сечения обычно приходится наиболее яркое или неожиданное музыкальное решение.

Кинорежиссер Сергей Эйзенштейн сценарий своего фильма «Броненосец Потёмкин» сознательно согласовывал с правилом золотого сечения, разделив ленту на пять частей. В первых трех разделах действие разворачивается на корабле, а в последних двух – в Одессе. Переход на сцены в городе и есть золотая середина фильма.

Источники: http://russian7.ru; http://n-t.ru.

Приглашаем к обсуждению темы в нашей группе — https://vk.com/dostoyanieplaneti

* * *

 

Рекомендуем к ознакомлению: 

Геометрия Великой пирамиды

Наука вторит индийским ведам

 

dostoyanieplaneti.ru

Золотое сечение – это… Золотое сечение пирамиды. Формула золотого сечения

Геометрия – точная и достаточно сложная наука, которая при всем этом является своеобразным искусством. Линии, плоскости, пропорции – все это помогает создавать много действительно прекрасных вещей. И как ни странно, в основе этого лежит именно геометрия в самых разных ее формах. В этой статье мы рассмотрим одну очень необычную вещь, которая непосредственно связанна с этим. Золотое сечение – это именно тот геометрических подход, о котором пойдет речь.

Форма предмета и ее восприятие

Люди чаще всего ориентируются на форму предмета для того, чтобы распознавать его среди миллионов других. Именно по форме мы определяем, что за вещь лежит перед нами или стоит вдали. Мы в первую очередь узнаем людей по форме тела и лица. Поэтому с уверенностью можем утверждать, что сама форма, ее размеры и вид – одна из самых важных вещей в восприятии человека.

Для людей форма чего бы то ни было представляет интерес по двум главным причинам: либо это диктуется жизненной необходимостью, либо же вызывается эстетическим наслаждением от красоты. Самое лучшее зрительное восприятие и ощущение гармонии и красоты чаще всего приходит, когда человек наблюдает форму, в построении которой использовались симметрия и особое соотношение, которое и называется золотым сечением.

Понятие золотого сечения

Итак, золотое сечение – это золотая пропорция, которая также является гармоническим делением. Для того чтобы объяснить это более понятно, рассмотрим некоторые особенности формы. А именно: форма является чем-то целым, ну а целое, в свою очередь, всегда состоит из некоторых частей. Эти части, вероятнее всего, обладают разными характеристиками, по крайней мере разными размерами. Ну а такие размеры всегда находятся в определенном соотношении как между собой, так и по отношению к целому.

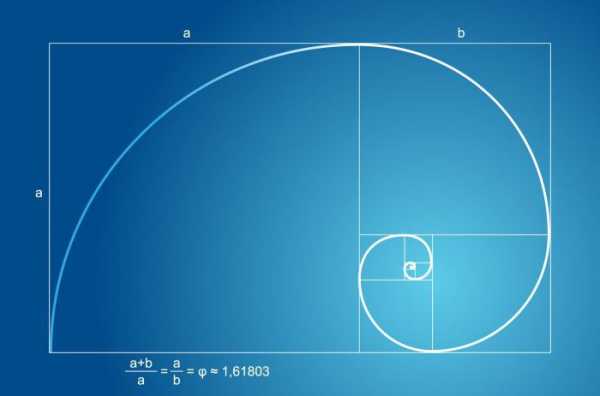
Значит, другими словами, мы можем утверждать, что золотое сечение – это соотношение двух величин, которое имеет свою формулу. Использование такого соотношения при создании формы помогает сделать ее максимально красивой и гармоничной для человеческого глаза.

Из древней истории золотого сечения

Соотношение золотого сечения часто используют в самых разных сферах жизни прямо сегодня. Но история этого понятия уходит еще в древние времена, когда только зарождались такие науки, как математика и философия. Как научное понятие золотое сечение вошло в обиход во времена Пифагора, а именно в VI веке до нашей эры. Но еще до того знания о подобном соотношении на практике использовали в Древнем Египте и Вавилоне. Ярким свидетельством этого являются пирамиды, для построения которых использовали именно такую золотую пропорцию.

Новый период

Эпоха Возрождения стала новым дыханием для гармонического деления, особенно благодаря Леонардо да Винчи. Это соотношение все больше начали использовать как в точных науках, таких как геометрия, так и в искусстве. Ученные и художники стали более глубоко изучать золотое сечение и создавать книги, рассматривающие этот вопрос.

Одна из самых важных исторических работ, связанных с золотой пропорцией, – это книга Луки Панчоли под названием «Божественная пропорция». Историки подозревают, что иллюстрации этой книги были выполнены самим Леонардо до Винчи.

Математика дает очень четкое определение пропорции, которое говорит о том, что она является равенством двух соотношений. Математически это можно выразить таким равенством: а:b=с:d, где а, b, с, d – это некоторые определенные значения.

Если рассматривать пропорцию отрезка, разделенного на две части, то можем встретить всего несколько ситуаций:

• Отрезок разделен на две абсолютно ровные части, а значит, АВ:АС= АВ:ВС, если АВ – это точна начала и конца отрезка, а С – точка, которая и разделяет отрезок на две равные части.
• Отрезок разделен на две неравные части, которые могут находиться в самом разном соотношении между собой, а значит, здесь они абсолютно непропорциональны.
• Отрезок разделен так, что АВ:АС= АС:ВС.

Что же касается золотого сечения, то это такое пропорциональное деление отрезка на неравные между собой части, когда весь отрезок относится к большей части, как и сама большая часть относится к меньшей. Существует и другая формулировка: меньший отрезок так относится к большему, как и больший ко всему отрезку. В математическом соотношении это выглядит следующим образом: а:b = b:с или с:b = b:а. Именно такой вид имеет формула золотого сечения.

Золотая пропорция в природе

Золотое сечение, примеры которого мы сейчас рассмотрим, относится к невероятным явлениям в природе. Это очень красивые примеры того, что математика – это не просто цифры и формулы, а наука, которая имеет более чем реальное отражение в природе и нашей жизни вообще.

Для живых организмов одна из главных жизненных задач – это рост. Такое стремление занять свое место в пространстве, по сути, осуществляется в нескольких формах – рост вверх, практически горизонтальное расстилание по земле или закручивание по спирали на некой опоре. И как бы ни было это невероятно, много растений растут в соответствии с золотой пропорцией.

Еще один почти невероятный факт – это соотношения в теле ящериц. Их тело выглядит достаточно приятно для человеческого глаза, и это возможно благодаря тому же золотому соотношению. Если быть точнее, то длина их хвоста относится к длине всего тела как 62 : 38.

Интересные факты о правилах золотого сечения

Золотое сечение – это поистине невероятное понятие, а значит, на протяжении всей истории мы можем встретить много действительно интересных фактов о такой пропорции. Представляем вам некоторые из них:

• Правило золотого сечения активно применялось в построении пирамид. Например, всемирно известные гробницы Тутанхамона и Хеопса возводили с использованием такого соотношения. И золотое сечение пирамиды до сих пор остается загадкой, ведь по сей день не известно, случайно или же специально выбирались такие размеры для их оснований и высот.
• Правило золотого сечения четко видно в фасаде Парфенона – одного из самых красивых сооружений в архитектуре Древней Греции.
• То же касается здания собора Парижской Богоматери (Нотр-Дам де Пари), то здесь не только фасады, но и другие части конструкции возводили, опираясь на эту невероятную пропорцию.
• В русской архитектуре можно встретить невероятно много примеров зданий, полностью соответствующих золотому сечению.
• Гармоничное деление присуще также и человеческому телу, а значит, и скульптуре, в частности, статуям людей. Например Аполлон Бельведерский – статуя, где у человека рост делится пупочной линией в золотом сечении.
• Живопись – отдельная история, особенно если учесть роль Леонарда да Винчи в истории золотого соотношения. Его известная Джоконда, конечно же, подлежит этому закону.

Золотое сечение в человеческом теле

В этом разделе нужно упомянуть очень значимую персону, а именно – С. Цейзинга. Это немецкий исследователь, который провел огромнейшую работу в сфере изучения золотой пропорции. Он опубликовал труд под названием «Эстетические исследования». В своей работе он представил золотое сечение как абсолютное понятие, которое является универсальным для всех явлений как в природе, так и в искусстве. Здесь можно вспомнить золотое сечение пирамиды наряду с гармоничной пропорцией человеческого тела и так далее.

Именно Цейзинг смог доказать, что золотое сечение, по сути, есть средним статистическим законом для человеческого тела. Это было показано на практике, ведь во время своей работы ему пришлось измерять очень много человеческих тел. Историки считают, что в этом опыте принимали участие более двух тысяч людей. По исследования Цейзинга, главный показатель золотого соотношения – это деление тела точкой пупка. Так, мужское тело со средним соотношением 13:8 немного ближе к золотому сечению, чем женское, где число золотого сечения составляет 8:5. Также золотую пропорцию можно наблюдать в других частях тела, таких как, например, рука.

О построении золотого сечения

На самом деле, построение золотого сечения – дело нехитрое. Как мы видим, еще древние люди справлялись с этим довольно легко. Что уже говорить о современных знаниях и технологиях человечества. В этой статье мы не будем показывать, как подобное можно сделать просто на листке бумаги и с карандашом в руках, но с уверенностью заявим, что это, на самом деле, возможно. Более того, сделать это можно далеко не одним способом.

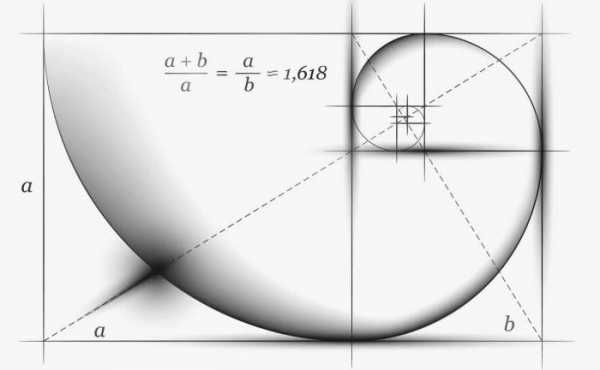
Так как это достаточно несложная геометрия, золотое сечение является довольно простым для построения даже в школе. Поэтому информацию об этом можно легко найти в специализированных книгах. Изучая золотое сечение 6 класс полностью способен понять принципы его построения, а значит, даже дети достаточно умны для того, чтобы осилить подобную задачу.

Золотая пропорция в математике

Первое знакомство с золотым сечением на практике начинается с простого деления отрезка прямой все в тех же пропорциях. Чаще всего это реализуется с помощью линейки, циркуля и, конечно же, карандаша.

Отрезки золотой пропорции выражают как бесконечную иррациональную дробь AE = 0,618…, если АВ принимается за единицу, ВЕ = 0,382… Для того чтобы сделать эти вычисления более практическими, очень часто используют не точные, а приближенные значения, а именно – 0,62 и 0,38. Если же отрезок АВ принимать за 100 частей, то большая его часть будет равна 62, ну а меньшая – 38 частям соответственно.

Главное свойство золотого соотношения можно выразить уравнением: х²-х-1=0. При решении мы получаем следующие корни: х_1,2=. Хотя математика и есть точной и строгой наукой, как и ее раздел – геометрия, но именно такие свойства, как закономерности золотого сечения, наводят таинственность на эту тему.

Гармония в искусстве через золотое сечение

Для того чтобы подвести итоги, рассмотрим коротко то, о чем уже говорили.

В основном под правило золотого соотношения подпадает много образцов искусства, где соблюдается соотношение близкое к 3/8 и 5/8. Это и есть грубая формула золотого сечения. В статье уже очень много упоминалось о примерах использования сечения, но мы еще раз посмотрим на него через призму древнего и современного искусства. Итак, самые яркие примеры из древних времен:

• Золотое сечение пирамиды Хеопса и Тутанхамона выражается буквально во всем: храмы, барельефы, предметы быта и, конечно же, украшения самых гробниц.
• Храм фараона Сети І в Абидосе славится рельефами с разными изображениями, и все это соответствует все тому же закону.

Что касается уже наверняка сознательного использования пропорции, то, начиная с времен Леонардо да Винчи, она вошла в использование практически во всех отраслях жизни – от науки и до искусства. Даже биология и медицина доказали, что золотое соотношение работает даже в живых системах и организмах.

fb.ru

Золотое сечение — Википедия. Что такое Золотое сечение

1,6180339887 4989484820 4586834365 6381177203 0917980576 2862135448 6227052604 6281890244 9707207204 1893911374 8475408807 5386891752 1266338622 2353693179 3180060766 7263544333 8908659593 9582905638 3226613199 2829026788 0675208766 8925017116 9620703222 1043216269 5486262963 1361443814 9758701220 3408058879 5445474924 6185695364 8644492410 4432077134 4947049565 8467885098 7433944221 2544877066 4780915884 6074998871 2400765217 0575179788 3416625624 9407589069 7040002812 1042762177 1117778053 1531714101 1704666599 1466979873 1761356006 7087480710 1317952368 9427521948 4353056783 0022878569 9782977834 7845878228 9110976250 0302696156 1700250464 3382437764 8610283831 2683303724 2926752631 1653392473 1671112115 8818638513 3162038400 5222165791 2866752946 5490681131 7159934323 5973494985 0904094762 1322298101 7261070596 1164562990 9816290555 2085247903 5240602017 2799747175 3427775927 7862561943 2082750513 1218156285 5122248093 9471234145 1702237358 0577278616 0086883829 5230459264 7878017889 9219902707 7690389532 1968198615 1437803149 9741106926 0886742962 2675756052 3172777520 3536139362

---

Первая тысяча знаков значения Φ^[1].

Золотое сечение (золотая пропорция, деление в крайнем и среднем отношении, гармоническое деление) — соотношение двух величин b и a, a > b, когда справедливо a/b = (a+b)/a. Число, равное отношению a/b, обычно обозначается прописной греческой буквой Φ{\displaystyle \Phi }, в честь древнегреческого скульптора и архитектора Фидия^[2], реже — греческой буквой τ{\displaystyle \tau }. Из исходного равенства нетрудно получить, что число

Φ=1+52{\displaystyle \Phi ={\frac {1+{\sqrt {5}}}{2}}}

Обратное число, обозначаемое строчной буквой φ{\displaystyle \varphi }^[2],

φ=1Φ=−1+52{\displaystyle \varphi ={\frac {1}{\Phi }}={\frac {-1+{\sqrt {5}}}{2}}}

Отсюда следует, что

φ=Φ−1{\displaystyle \varphi =\Phi -1}.

Для практических целей ограничиваются приблизительным значением Φ{\displaystyle \Phi } = 1,618 или Φ{\displaystyle \Phi } = 1,62. В процентном округлённом значении золотое сечение — это деление какой-либо величины в отношении 62 % и 38 %.

Исторически изначально золотым сечением именовалось деление отрезка АВ точкой С на две части (меньший отрезок АС и больший отрезок ВС), чтобы для длин отрезков было верно AC/BC = BC/AВ. Говоря простыми словами, золотым сечением отрезок рассечён на две неравные части так, что меньшая часть относится к большей, как большая ко всему отрезку. Позже это понятие было распространено на произвольные величины.

Иллюстрация к определению

Число Φ{\displaystyle \Phi } называется также золотым числом.

Золотое сечение имеет множество замечательных свойств, но, кроме того, ему приписывают и многие вымышленные свойства^[3][4][5].

История

В дошедшей до нас античной литературе деление отрезка в крайнем и среднем отношении (ἄκρος καὶ μέσος λόγος) впервые встречается в «Началах» Евклида (ок. 300 лет до н. э.), где оно применяется для построения правильного пятиугольника.

Лука Пачоли, современник и друг Леонардо да Винчи, усматривал в этом отношении «божественную суть», выражающую триединство Бога Отца, Сына и Святого Духа^[6].

Неизвестно точно, кто и когда именно впервые ввел в обращение термин «золотое сечение». Несмотря на то, что некоторые авторитетные авторы связывают появление этого термина с Леонардо да Винчи в XV веке^[7] или относят появление этого термина к XVI веку^[8], самое раннее употребление этого термина находится у Мартина Ома в 1835 году в примечании ко второму изданию его книги «Чистая элементарная математика»^[9], в котором Ом пишет, что это сечение часто называют золотым сечением (нем. goldener Schnitt). Из текста примечания Ома следует, что Ом не придумал этот термин сам^[10][11], хотя некоторые авторы утверждают обратное^[12]. Тем не менее, исходя из того, что Ом не употребляет этот термин в первом издании своей книги^[13], Роджер Герц-Фишлер делает вывод о том, что этот термин, возможно, появился в первой четверти XIX века.^[14]Марио Ливио считает, что он получил популярность в устной традиции около 1830 года.^[15] В любом случае, этот термин стал распространён в немецкой математической литературе после Ома.^[16]

Математические свойства

1Φ=φ=tg⁡(arctg⁡(2)2)=21+1+22=21+5=5−12.{\displaystyle {\frac {1}{\Phi }}=\varphi =\operatorname {tg} \left({\frac {\operatorname {arctg} (2)}{2}}\right)={\frac {2}{1+{\sqrt {1+2^{2}}}}}={\frac {2}{1+{\sqrt {5}}}}={\frac {{\sqrt {5}}-1}{2}}.}

• Φ{\displaystyle \Phi } представляется в виде бесконечной цепочки квадратных корней:

  Φ=1+1+1+1+….{\displaystyle \Phi ={\sqrt {1+{\sqrt {1+{\sqrt {1+{\sqrt {1+\dots }}}}}}}}.}

• Φ{\displaystyle \Phi \;} представляется в виде бесконечной цепной дроби

  Φ=1+11+11+11+…,{\displaystyle \Phi =1+{\cfrac {1}{1+{\cfrac {1}{1+{\cfrac {1}{1+\dots }}}}}},}

подходящими дробями которой служат отношения последовательных чисел Фибоначчи Fn+1Fn{\displaystyle {\frac {F_{n+1}}{F_{n}}}}. Таким образом,

Отрезание квадрата от прямоугольника, построенного по принципу золотого сечения

• Отрезав квадрат от прямоугольника, построенного по принципу золотого сечения, мы получаем новый, уменьшенный прямоугольник с тем же отношением сторон Φ=a/b{\displaystyle \Phi =a/b}, что и у исходного прямоугольника Φ=(a+b)/a{\displaystyle \Phi =(a+b)/a}.

Золотое сечение в пятиконечной звезде

• В правильной пятиконечной звезде каждый отрезок делится пересекающим его отрезком в золотом сечении. На приведённом рисунке отношения красного отрезка к зелёному, зелёного к синему и синего к пурпурному равны Φ{\displaystyle \Phi }. Кроме того, отношение красного отрезка к расстоянию между соседними вершинами звезды, которое равно зелёному отрезку, также равно Φ{\displaystyle \Phi }.

Построение золотого сечения

Φ=|AB||AE|=|AE||BE|.{\displaystyle \Phi ={\frac {|AB|}{|AE|}}={\frac {|AE|}{|BE|}}.}

Другой способ построить отрезок, равный по длине числу золотого сечения

• Другой способ построить отрезок, равный по длине числу золотого сечения, — начертить сначала квадрат ABCD со стороной 1. После этого одну из сторон, например сторону AD, разделить точкой E пополам, так что AE=DE=1/2. От точки B или C до точки E провести гипотенузу треугольника АВЕ или DCE. Согласно теореме Пифагора ВE=СE=52{\displaystyle {\frac {\sqrt {5}}{2}}}. Затем провести дугу с центром в точке Е от точки В или точки С до момента её пересечения с продолжением стороны АD (точкой пересечения дуги и продолжения стороны АD пусть будет точка Н). Как радиусы круга BE=СЕ=ЕН. Так как АН=АЕ+ЕН, результатом будет отрезок АН длиной Φ{\displaystyle \Phi }. Так как DH=EH-ED, другим результатом будет отрезок DH длиной φ{\displaystyle \varphi }^[17].

• Отношение диагонали правильного пятиугольника к стороне равно золотому сечению.
• Значения дроби после запятой для Φ{\displaystyle \Phi }, 1Φ{\displaystyle {\frac {1}{\Phi }}} и Φ2{\displaystyle \Phi ^{2}} в любой системе счисления будут равны^[18].
• ∑n=1∞(−1)n+1n2(2nn)=2ln2⁡φ{\displaystyle \sum _{n=1}^{\infty }{\frac {(-1)^{n+1}}{n^{2}{\binom {2n}{n}}}}=2\ln ^{2}\varphi }

Тогда как ∑n=1∞1n2(2nn)=π218{\displaystyle \sum _{n=1}^{\infty }{\frac {1}{n^{2}{\binom {2n}{n}}}}={\frac {\pi ^{2}}{18}}}^{[источник не указан 992 дня]}

Золотое сечение в науке

Общее сопротивление этой бесконечной цепи равно Фr.

Золотое число возникает в разных задачах, в том числе в физике. Например, бесконечная электрическая цепь, приведенная на рисунке имеет общее сопротивление (между двумя левыми концами) Ф·r.

Отношение амплитуд колебаний и частот ~ Ф.

Существуют колебательные системы, физические характеристики которых (отношения частот, амплитуд и др.) пропорциональны золотому сечению. Самый простой пример — система из двух шариков, соединенных последовательно пружинами одинаковой жесткости (см. рисунок).

Полностью эти две задачи рассматривается в книге «В поисках пятого порядка», глава «Две простые задачки»^[19]. Более сложные примеры на механические колебания и их обобщения рассматриваются в этой же книге, в главе «Обобщения одной простой задачи по механике». В книге приведено много примеров проявления и применения золотого сечения в различных областях наук — небесной механике, физике, геофизике, биофизике, физической химии, биологии, физиологии.

Золотое сечение сильно связано с симметрией пятого порядка, наиболее известными трехмерными представителями которой являются додекаэдр и икосаэдр. Можно сказать, что всюду, где в структуре проявляются додекаэдр, икосаэдр или их производные, там в описании будет появляться и золотое сечение. Например, в пространственных группировках из Бора: В-12, В-50, В-78, В-84, В-90, …, В-1708, имеющих икосаэдрическую симметрию^[20]. Молекула воды, у которой угол расхождения связей Н-О равен 104.7⁰ , то есть близок к 108 градусам (угол в правильном пятиугольнике), может соединяться в плоские и трехмерные структуры с симметрией пятого порядка. Так в разреженной плазме был обнаружен Н⁺(Н₂0)₂₁, который представляет из себя ион Н₃0⁺, окруженный 20 молекулами воды, расположенными в вершинах додекаэдра^[21]. В 80-х годах XX века были получены клатратные соединения, содержащие гексааквакомплекс кальция, окруженный 20 молекулами воды, расположенными в вершинах додекаэдра^[22]. Есть и клатратные модели воды, в которых обыкновенная вода отчасти состоит из молекул воды, соединенных в структуры с симметрией пятого порядка. Такие структуры могут состоять из 20, 57, 912 молекул воды^[23].

Золотое сечение и гармония в искусстве

Золотое сечение и зрительные центры

Некоторые из утверждений в доказательство гипотезы знания древними правила золотого сечения:

• Пропорции пирамиды Хеопса, храмов, барельефов, предметов быта и украшений из гробницы Тутанхамона свидетельствуют, что египетские мастера пользовались соотношениями золотого сечения при их создании.
• Согласно Ле Корбюзье, в рельефе из храма фараона Сети I в Абидосе и в рельефе, изображающем фараона Рамзеса, пропорции фигур соответствуют золотому сечению. В фасаде древнегреческого храма Парфенона также присутствуют золотые пропорции. В циркуле из древнеримского города Помпеи (музей в Неаполе) также заложены пропорции золотого деления, и т. д. При обсуждении оптимальных соотношений сторон прямоугольников (размеры листов бумаги A0 и кратные, размеры фотопластинок (6:9, 9:12) или кадров фотоплёнки (часто 2:3), размеры кино- и телевизионных экранов — например, 4:3 или 16:9) были испытаны самые разные варианты. Оказалось, что большинство людей не воспринимает золотое сечение как оптимальное и считает его пропорции «слишком вытянутыми»^{[источник не указан 3360 дней]}.
• Следует отметить, что сама пропорция является, скорее, эталонным значением, матрицей, отклонения от которой у биологических видов, возможно, вызваны приспособлением к окружающей среде в процессе жизни. Примером таких «отклонений» может служить морская камбала.

Примеры сознательного использования

Начиная с Леонардо да Винчи, многие художники сознательно использовали пропорции «золотого сечения». Российский зодчий И. В. Жолтовский использовал золотое сечение в своих проектах^[24]. Иоганн Себастьян Бах в своей трёхголосной инвенции E-dur № 6 BWV 792 использовал двухчастную форму, в которой соотношение размеров частей соответствует пропорциям золотого сечения. 1 часть — 17 тактов, 2 часть — 24 такта (небольшие несоответствия выравниваются за счёт ферматы в 34 такте)^{[источник не указан 585 дней]}.

Одним из современных примеров применения золотого сечения может служить мозаика Пенроуза.

Золотое сечение в биологии и медицине

Золотое сечение в природе

Живые системы также обладают свойствами, характерными для «золотого сечения». Например: пропорции тел, спиральные структуры или параметры биоритмов^{[25][неавторитетный источник?]} и др.

См. также

Примечания

1. ↑ Взята из примера результата компьютерного расчета (1996 года) с гораздо большим числом знаков, чем 1000 Golden ratio 1000 digits
2. ↑ ^{1 2} Савин А. Число Фидия — золотое сечение (рус.) // «Квант» : Научно-популярный физико-математический журнал (издается с января 1970 года). — 1997. — № 6.
3. ↑ Радзюкевич А. В. Красивая сказка о «золотом сечении»
4. ↑ Mario Livio, The Golden Ratio: The Story of Phi, The World’s Most Astonishing Number
5. ↑ Devlin’s Angle, The Myth That Will Not Go Away
6. ↑ В. Лаврус, Золотое сечение
7. ↑ François Lasserre. The birth of mathematics in the age of Plato. — American Research Council, 1964-01-01. — 200 с. — P. 76.
8. ↑ Boyer, Carl B. A History of Mathematics. — Second Edition. — John Wiley & Sons, Inc., 1991. — P. 50. — ISBN 0-471-54397-7.
9. ↑ Martin Ohm. Die reine Elementar-Mathematik. — 2-е изд. — Jonas Verlags-buchhandlung, 1835. — С. 194. — 454 с.
10. ↑ Herz-Fischler, 2013, p. 168.
11. ↑ Livio, 2008, p. 6-7.
12. ↑ Василенко С. Л. Знак-символ золотого сечения // Академия Тринитаризма. — М., 05.02.2011. — № Эл № 77-6567, публ. 16335.
13. ↑ Martin Ohm. Die reine Elementar-Mathematik. — 1-е изд.. — Berlin, 1826. — 492 с. — P. 188.
14. ↑ Herz-Fischler, 2013, p. 169.
15. ↑ Livio, 2008, p. 7.
16. ↑ Herz-Fischler, 2013, p. 169-170.
17. ↑ Тони Крилли. Математика: 50 идей, о которых нужно знать = 50 Mathematical Ideas you really need to know. — Phantom Press. — 209 с. — ISBN 9785864716700.
18. ↑ Системы счисления.
19. ↑ Ковалев А.Н. В поисках пятого порядка. — 2017. — 374 с. — ISBN 978-5-4485-3753-0.
20. ↑ Современная Кристаллография / под ред. Вайнштейна Б. К.. — Т.2. — М.: Мир, 1979.
21. ↑ Holland P. M. Casteiman A. W. A model for the formation and stabilization of chorqed water cluthrates // J. Chem. Phys.. — 1980. — Т. 72, № 1(11). — С. 5984.
22. ↑ Электромагнитные поля в биосфере. — Сборник трудов конференции, Т.2. — М., 1984. — С. 22.
23. ↑ Зенин С.В. Структурированное состояние воды как основа управления поведением и безопасностью живых систем. — Диссертация докт. биол. наук. — М., 1999.
24. ↑ Золотой запас зодчества Архивная копия от 29 января 2009 на Wayback Machine
25. ↑ Цветков, В. Д. Сердце, золотое сечение и симметрия. — Пущино: ПНЦ РАН, 1997. — 170 с.

Литература

• Аракелян Г. Б. Математика и история золотого сечения. — М.: Логос, 2014, 404 с. — ISBN 978-5-98704-663-0.
• Бендукидзе А. Д. Золотое сечение «Квант» № 8, 1973
• Васютинский Н. А. Золотая пропорция. — М.: Молодая гвардия, 1990. — 238[2]c. — (Эврика).
• Власов В. Г. Новый энциклопедический словарь изобразительного искусства: В 10 т. — Т.3. — СПб.: Азбука-Классика, 2005. — С.725-732.
• Власов В. Г. Искусство России в пространстве Евразии. — Т.3. Классическое искусствознание и «русский мир». — СПб.: Дмитрий Буланин, 2012. — С.156-192.
• Мазель, Л.А. Опыт исследования золотого сечения в музыкальных построениях в свете общего анализа форм // Музыкальное образование. – 1930. – № 2. – С. 24-33.
• Сабанеев Л. Л. Этюды Шопена в освещении закона золотого сечения. Опыт позитивного обоснования законов формы // Искусство. — 1925. — № 2. — С. 132—145; 1927. — № 2-3. — С. 32-56.
• Шмигевский Н. В. Формула совершенства // Страна знаний. — 2010. — № 4. — С.2-7.
• Mario Livio. The Golden Ratio: The Story of PHI, the World’s Most Astonishing Number. — Crown/Archetype, 2008. — 303 с. — ISBN 9780307485526. Русский перевод в

Марио Ливио. φ – Число Бога. Золотое сечение – формула мироздания. — Litres, 2015-04-17. — 481 с. — ISBN 9785457762732.

Ссылки

wiki.sc

Калькулятор золотого сечения (золотой пропорции) онлайн

Золотое сечение — это особое соотношение сторон фигуры, которое наиболее приятно для созерцания. Это число известно с античных времен, а ученые эпохи Возрождения называли его божественной пропорцией. Число Фи — золотое сечение, приблизительно равное 1,618.

История

Особую красоту деления отрезка на стороны в соотношении 1/1,618 заметили еще античные ученые. Евклид в своих началах использовал этот метод при построении пентагона, а пифогорейцы рассматривали весь мир как царство математической гармонии и уделяли большое внимание соотношению 1/1,618. В 1202 году Леонардо Фибоначчи вывел особую последовательность, отношение членов которой стремилось к числу Фибоначчи. Лука Пачоли, один из величайших алгебраистов Италии, назвал это соотношение божественной пропорцией, связав свойства бога с числом Фи. Именно с этого момента золотое сечение начало активно использоваться в работах художников эпохи Возрождения и получило буквально мистический статус. По словам Кеплера, число Фи — бесценная жемчужина математики.

Число Фи в математике

Золотое сечение часто встречается в геометрии. Золотой прямоугольник — фигура на плоскости, длина и ширина которой соотносятся как 1/1,618. Примечательное свойство такого прямоугольника состоит в том, что при удалении из фигуры любого квадрата образуется новый прямоугольник с точно таким же соотношением сторон. Стоит упомянуть и пентаграмму — звездчатый многоугольник, стороны которого пересекаются в соответствии с правилом золотого сечения.

В арифметике число Фи встречается в упоминаемой выше последовательности Фибоначчи, так как lim(Fn/Fn-1) -> Фи. Кроме того, золотое сечение имеет интересное представление в других формах записи. Так, Фи представляется как бесконечная цепочка квадратных корней из единицы. А если привести Фи к цепному виду, то получится бесконечная дробь вида [1; 1, 1, 1, 1, 1…]

Число Фи в реальности

Мистический ореол вокруг золотого сечения возник благодаря такому явлению как «золотой числизм». Энтузиасты, задавшиеся целью найти эту пропорцию в как можно большем количестве реальных объектов или явлений, часто подгоняли результаты. К примеру, храм Парфенон всегда присутствует в списке объектов, которые построены с учетом божественной пропорции. Однако на деле соотношение ширины храма к его высоте составляет 1,74, а если исключить фронтон, то и вовсе 3.

После придания числу божественных свойств, многие художники и музыканты начали сознательно использовать это соотношение в своих работах. Леонардо да Винчи, Альбрехт Дюрер, Иоганн Бах, Ле Корбюзье, Густав Фехнер намеренно придавали своим произведениям форму, соответствующую числу Фи. Одним из современных примеров использования золотого сечения является мозаика Пенроуза — метод непериодического разбиения плоскости.

Несмотря на явное преувеличение свойств золотой пропорции, она все же встречается в реальности. Большинство спиралевидных объектов связны с числом Фи: раковины моллюсков, атмосферные вихри и даже галактики действительно соответствуют божественной пропорции.

Калькулятор золотого сечения

Если вы хотите использовать божественную пропорцию в своей работе, то наш калькулятор к вашим услугам. Для определения сторон золотого прямоугольника вам понадобится ввести одну из сторон, а программа определит вторую, соответствующую правилу золотого сечения. Прелесть калькулятора состоит в том, что он не просто умножает сторону на 1,618, а подбирает целое значение. Именно поэтому вам потребуется оперировать целыми числами, что удобно на практике.

Пример из реальной жизни

Живопись

Допустим, вы хотите сделать приятную с точки зрения математики картину, следовательно, вам нужно нарисовать ее на золотом прямоугольнике. Вам потребуется заказать холст определенного размера, и чтобы определить его размеры, используйте наш калькулятор. Пусть вы хотите писать на холсте, длина которого составит 120 см. Как узнать необходимую ширину? Введите это значение в ячейку A и получите ответ, равный 74 см.

Заключение

Божественная пропорция — мистическое соотношение, которое занимает умы математиков уже несколько тысячелетий. Возможно, именно число Фи содержит ответы на вечные вопросы о тайнах мироздания. Если вам потребуется создать объекты, соответствующие золотому сечению, используйте наш калькулятор, при помощи которого вы сможете подобрать целые числа.

bbf.ru