Рисунок сферы: Урок 8. сфера и шар — Геометрия — 11 класс

Академический рисунок.| Конструктивное рисование Шар и Куб.

Что такое «перспектива» в рисунке?  

Перспектива — («видеть насквозь»). Выделяют понятия линейной, прямой, обратной и воздушной перспективы. Для верного построения в академическом рисунке, при передаче пространства и конструктивном построении предметов, используется прямая и воздушная перспектива.

Закономерности линейной перспективы:

• Параллельные линии в горизонтальной плоскости, уходящие в глубину, сойдутся в точке схода на линии горизонта. В пределах рисунка или за пределами.
• Предметы одного размера, находящиеся на разной удаленности кажутся разными по размеру.
• Линия горизонта проходит горизонтально и параллельно полу на уровне глаз, независимо сидит или стоит наблюдатель.

Конструктивное построение куба.

Академический рисунок. Тональное решение куба.

Куб — элементарная геометрическая фигура, рисование куба научит мыслить в рисунке объёмно и конструктивно.

Эта фигура состоит из 6 поверхностей, верхней, нижней, переднюю, задней и двух боковых. Освоив логику рисования куба, её применяют к построению других предметов. Например: стульев, шкафов, комнат, одним словом всего, что содержит в себе логику формы куба и строится по тем же принципам.

Приступим непосредственно к работе над кубом. Как уже говорилось, одной из задач академического рисунка — обозначить трехмерность. На этапе построения куба необходимо построить грани и плоскости, не теряя при этом пропорций. Правильно построенный куб должен выглядеть как конструкция, каркас к будущей фигуре. Вертикальные грани — перпендикулярны полу и параллельны вертикальному краю листа. Куб не должен разъезжаться, казаться деформированным, стороны и грани ощущаются параллельными.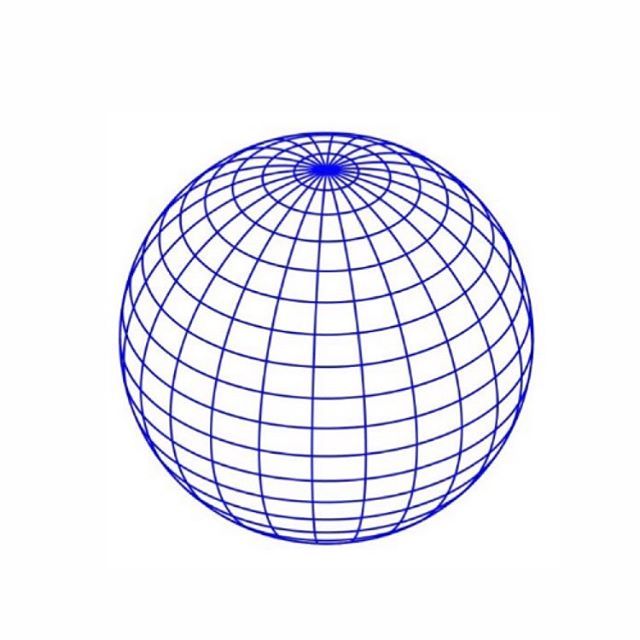

Рисование куба кажется неинтересным и бесполезным делом, но это не так. Стоит приложить усилия, закончить, и оценить насколько фигура получилась удачной. Это упражнение даст понимание законов построения в академическом рисунке. Уроки рисунка Киев.

Рисование перспективы сферы.

Академический рисунок. Тональное решение шара.

Сфера или шар — геометрический примитив. И как ни странно, при своей сложности восприятия в академическом рисунке, шар имеет необходимые поверхности для существования трехмерного пространства и вписывается в уже знакомый куб. Помните, что при вписывании правильного шара в куб, вершина будет в центре стороны куба, который находится пересечением диагоналей этой стороны.

Самым простым способом создания правильного шара — вписать в квадрат.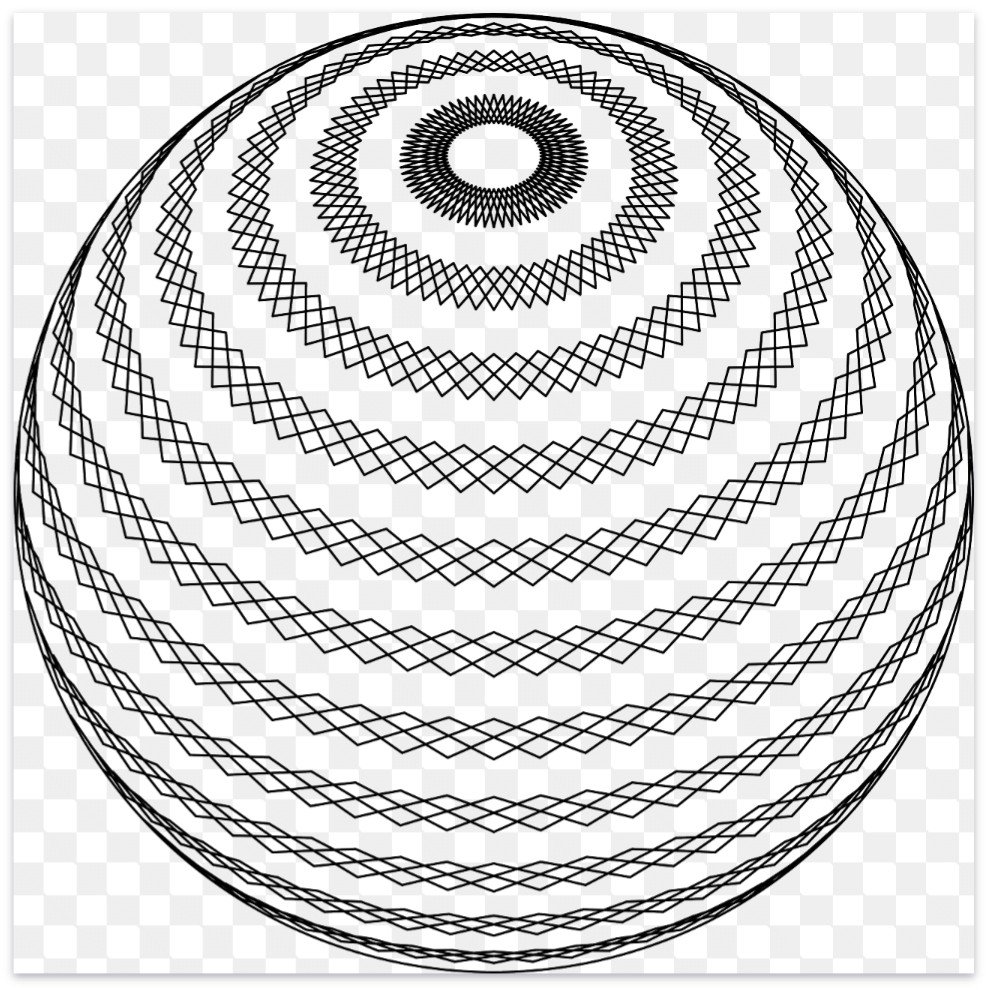 Стоит провести две осевые, придерживаясь вертикали и горизонтали. От центра пересечения осевых – согласно пропорциональным отношениям шара с другими геометрическими предметами (если они есть) —  отложить одинаковые отрезки на осевых и построить окружность. Таким образом, получаем двухмерную фигуру под названием круг. Шаром, эта плоская фигура, станет только после добавления третьей плоскости — глубины. 

Как же создать объем шара? Нужно горизонтальную осевую раскрыть до состояния квадратной плоскости в перспективе (трапеция). Положения плоскости будет зависеть от угла зрения наблюдателя на предмет. Вписанный круг в квадрат плюс окружное сечение в виде эллипса, через четыре точки и создадут объёмность изображаемого объекта. Аналогично разворачиваем и вертикальную осевую до состояния плоскости (вертикально расположенной трапеции), это поможет сделать конструктивный рисунок изображаемого объекта и дадут понимание об объёме объекта. Так можно получить две вершины и указать самую высокую точку шара и точку опоры.

Конструктивное построение в академическом рисунке.

Конструктивное построение натюрморта.

К конструктивному построению геометрических фигур художник приступает только после того, как лист правильно скомпонован и пропорции взяты верно. Проверка пропорций в рисунке происходит  несколько раз в начале работы. Конструктивное построение — важнейший этап, и происходит он только после верной компоновки и взятия сходства. Приступая к построению, не отвлекайтесь на внешние эффекты и детали.

Курсы рисования карандашом Киев

В рисунке необходимо создать иллюзию объёма, сохраняя ощущение объема, и ощущение конструкции в заданном ракурсе. Помните, на каждом из этапов рисования фигуры должны выглядеть объёмно.

Пространство — среда, в которой размещен рисуемый предмет, будь то простая геометрическая фигура или обнаженная модель. Объекты в пространстве имеют свою высоту, ширину, глубину, то есть находятся в трёхмерном пространстве. В начале обучения рисунку, умение передавать объём лучше закрепляется в рисовании простых фигур, ведь на нее действуют те же законы, что и на живую модель.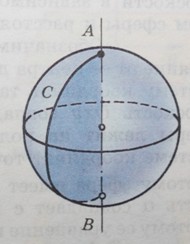

Старайтесь не спешить рисовать сложные формы, поработайте над конструктивным построением куба, шара, призм и конусов, это крайне важно. Школа рисования Киев.

Сфера, шар, сегмент и сектор. Формулы и свойства

Определение.

Сфера (поверхность шара) — это совокупность всех точек в трехмерном пространстве, которые находятся на одинаковом расстоянии от одной точки, называемой центром сферы (О).

Сферу можно описать, как объёмную фигуру, которая образуется вращением окружности вокруг своего диаметра на 180° или полуокружности вокруг своего диаметра на 360°.

Определение.

Шар — это совокупность всех точек в трехмерном пространстве, расстояние от которых не превышает определенного расстояния до точки, называемой центром шара (О) (совокупность всех точек трехмерного пространства ограниченных сферой).

Шар можно описать как объёмную фигуру, которая образуется вращением круга вокруг своего диаметра на 180° или полуокружности вокруг своего диаметра на 360°.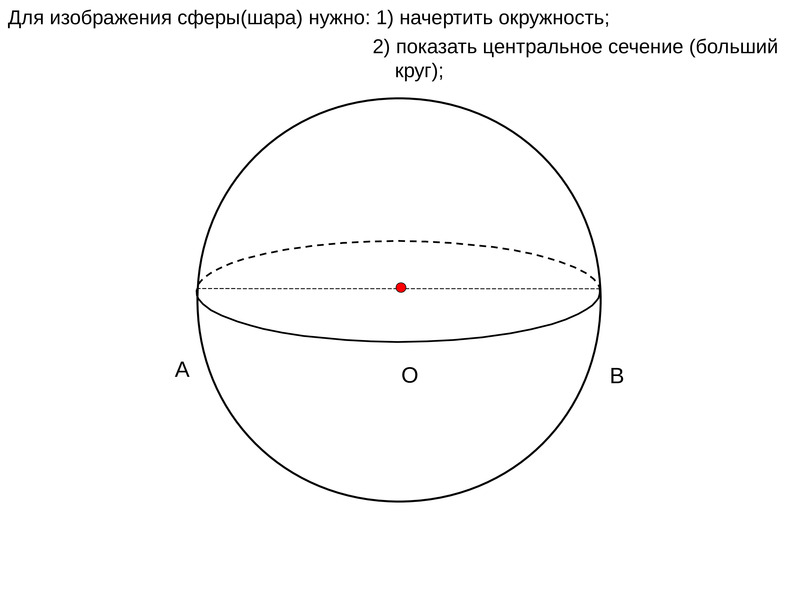

Определение. Радиус сферы (шара) (R) — это расстояние от центра сферы (шара) O к любой точке сферы (поверхности шара).

Определение. Диаметр сферы (шара) (D) — это отрезок, соединяющий две точки сферы (поверхности шара) и проходящий через ее центр.

Формула. Объём шара: Формула. Площадь поверхности сферы через радиус или диаметр:

S = 4πR² = πD²

Уравнение сферы

1. Уравнение сферы с радиусом R и центром в начале декартовой системе координат:

x² + y² + z² = R²

2. Уравнение сферы с радиусом R и центром в точке с координатами (x₀, y₀, z₀) в декартовой системе координат:

(x — x₀)² + (y — y₀)² + (z — z₀)² = R²

3. Параметрическое уравнение сферы с центром в точке (x₀, y₀, z₀):
x = x₀ + R · sin θ · cos φy = y₀ + R · sin θ · sin φz = z₀ + R · cos θ
где θ ϵ [0,π], φ ϵ [0,2π].

Определение. Диаметрально противоположными точками называются любые две точки на поверхности шара (сфере), которые соединены диаметром.

Основные свойства сферы и шара

1. Все точки сферы одинаково удалены от центра.

2. Любое сечение сферы плоскостью является окружностью.

3. Любое сечение шара плоскостью есть кругом.

4. Сфера имеет наибольший объём среди всех пространственных фигур с одинаковой площадью поверхности.

5. Через любые две диаметрально противоположные точки можно провести множество больших окружностей для сферы или кругов для шара.

6. Через любые две точки, кроме диаметрально противоположных точек, можно провести только одну большую окружность для сферы или большой круг для шара.

7. Любые два больших круга одного шара пересекаются по прямой, проходящей через центр шара, а окружности пересекаются в двух диаметрально противоположных точках.

8. Если расстояние между центрами любых двух шаров меньше суммы их радиусов и больше модуля разности их радиусов, то такие шары пересекаются, а в плоскости пересечения образуется круг.

Секущая, хорда, секущая плоскость сферы и их свойства

Определение. Секущая сферы — это прямая, которая пересекает сферу в двух точках. Точки пересечения называются точками протыкания поверхности или точками входа и выхода на поверхности.

Определение. Хорда сферы (шара) — это отрезок, соединяющий две точки сферы (поверхности шара).

Определение. Секущая плоскость — это плоскость, которая пересекает сферу.

Определение. Диаметральная плоскость — это секущая плоскость, проходящая через центр сферы или шара, сеченме образует соответственно большую окружность и большой круг. Большая окружность и большой круг имеют центр, который совпадают с центром сферы (шара).

Любая хорда, проходящая через центр сферы (шара) является диаметром.

Хорда является отрезком секущей прямой.

Расстояние d от центра сферы до секущей всегда меньше чем радиус сферы:

d < R

Расстояние m между секущей плоскостью и центром сферы всегда меньше радиуса R:

m < R

Местом сечения секущей плоскости на сфере всегда будет малая окружность, а на шаре местом сечения будет малый круг. Малая окружность и малый круг имеют свои центры, не совпадающих с центром сферы (шара). Радиус r такого круга можно найти по формуле:

r = √R² — m²,

где R — радиус сферы (шара), m — расстояние от центра шара до секущей плоскости.

Определение. Полусфера (полушар) — это половина сферы (шара), которая образуется при ее сечении диаметральной плоскостью.

Касательная, касательная плоскость к сфере и их свойства

Определение.Касательная к сфере — это прямая, которая касается сферы только в одной точке.

Определение.Касательная плоскость к сфере — это плоскость, которая соприкасается со сферой только в одной точке.

Касательная пряма (плоскость) всегда перпендикулярна радиусу сферы проведенному к точке соприкосновения

Расстояние от центра сферы до касательной прямой (плоскости) равно радиусу сферы.

Определение. Сегмент шара — это часть шара, которая отсекается от шара секущей плоскостью. Основой сегмента называют круг, который образовался в месте сечения. Высотой сегмента h называют длину перпендикуляра проведенного с середины основы сегмента к поверхности сегмента. Формула. Площадь внешней поверхности сегмента сферы с высотой h через радиус сферы R:

S = 2πRh

Формула. Объём сегмента сферы с высотой h через радиус сферы R: Определение. Срез шара — это часть шара, которая образуется в результате его сечения двумя параллельными плоскостями и находится между ними. Определение. Сектором называется часть шара, ограниченная совокупностью всех лучей, исходящих из центра шара О и образующих круг на его поверхности с радиусом r. Формула. Площадь поверхности сектора S с высотой O₁H (h) через радиус шара OH (R):

S = πR(2h + √2hR — h²)

Формула. Объём сектора V с высотой O₁H (h) через радиус шара OH (R):

Определение. Касательными сферами (шарами) называются любые две сферы (шара), которые имеют одну общую точку соприкосновения. Если расстояние между центрами больше суммы радиусов, то фигуры не касаются и не пересекаются.

Определение. Концентрическими сферами называются любые две сферы, которые имеют общий центр и радиусы различной длины.

Сфера и шар / Многогранники / Справочник по геометрии 7-9 класс

1. Главная
2. Справочники
3. Справочник по геометрии 7-9 класс
4. Многогранники
5. Сфера и шар

Сфера — поверхность, состоящая из всех точек пространства, расположенных на заданном расстоянии от данной точки.

Центр сферы — данная точка (точка О на рисунке выше).

Радиус сферы — данное расстояние (R на рисунке выше), также это любой отрезок, соединяющий центр сферы с какой-либо ее точкой.

Диаметр сферы — отрезок, соединяющий две точки сферы и проходящий через ее центр. Диаметр сферы в два раза больше ее радиуса, т.е. если радиус сферы — R, то ее диаметр — 2R.

Определение

Шар — тело, ограниченное сферой.

Центр, радиус и диаметр сферы называются также центром, радиусом и диаметром шара. Шар радиуса R с центром О содержит все точки пространства, расположенные от точки О на расстоянии, не превышающем R (включая и саму точку О), и не содержит других точек.

Шар также может быть получен вращением полукруга вокруг его диаметра. При этом сфера образуется в результате вращения полуокружности.

Объем шара

Доказательство

Дано: шар радиуса R и объемом V.

Доказать: .

Доказательство:

Воспользуемся принципом Кавальери*. Рассмотрим два тела: половину шара радиуса R и тело Т, представляющее собой цилиндр радиуса R с высотой R, из которого вырезан конус с радиусом основания и высотой R. Представим себе, что оба тела «стоят» на плоскости (смотри рисунок ниже). Проведем секущую плоскость , параллельную плоскости и пересекающую радиус шара ОА, перпендикулярный к плоскости , в точке А₁, а высоту ВН конуса — в точке В₁.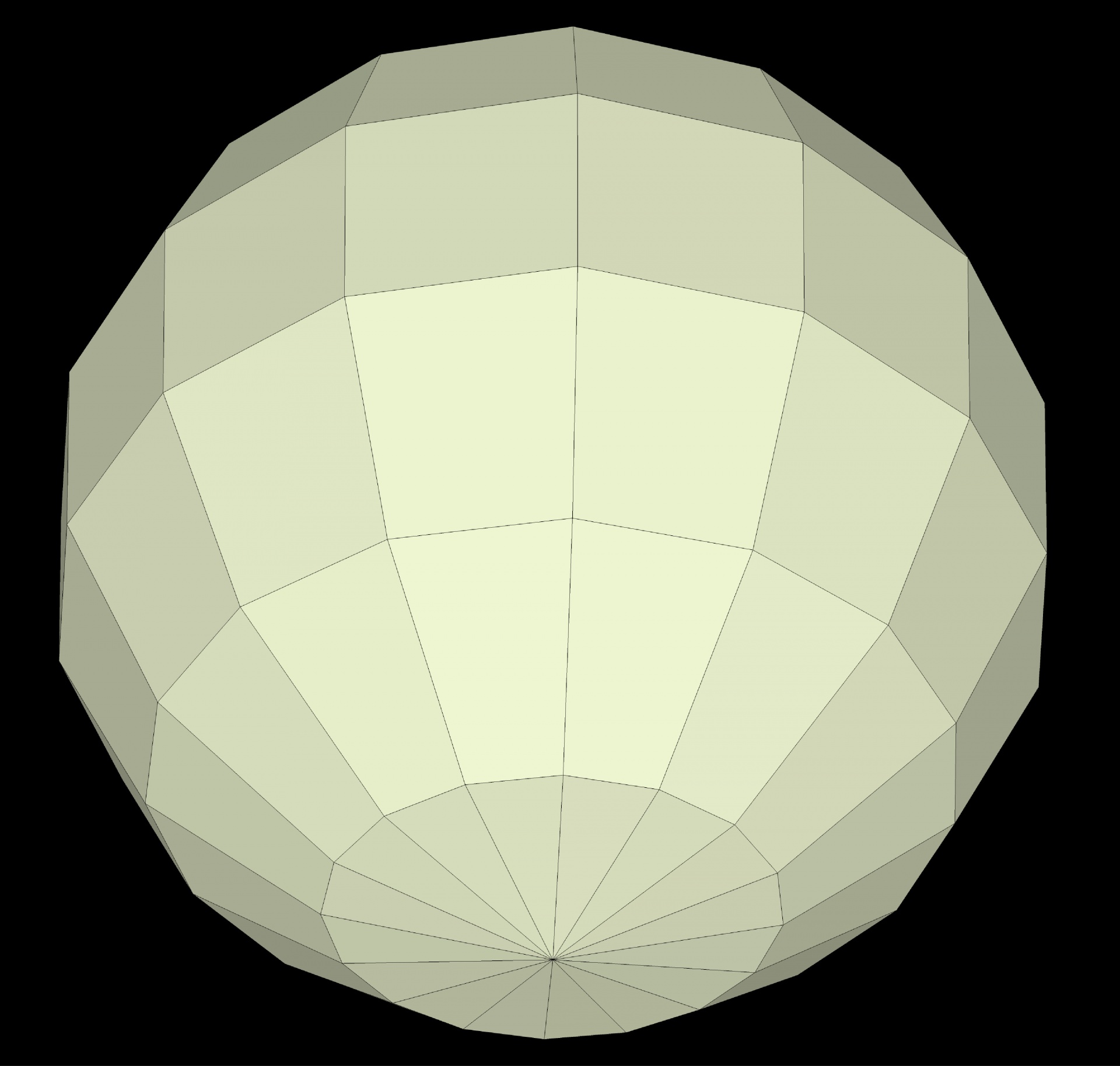

Сечение половины шара представляет собой круг, по теореме Пифагора радиус этого круга . Поэтому площадь этого круга .

Сечение тела Т представляет собой кольцо, площадь которого равна разности площадей двух кругов: круга радиуса R и круга радиуса В₁В₂ (смотри рисунок выше), т.е. равна .  ВВ₁В₂ подобен  ВНК по двум углам ( В — общий,  ВВ₁В₂=  ВНК = 90⁰), при этом ВН = НК = R, следовательно, и В₁В₂= ВВ₁ , кроме того, ВВ₁ = ОА₁ (т.к. параллельные плоскости отсекают от параллельных прямых равные отрезки), значит, площадь сечения тела Т равна .

Получаем, что площадь сечения половины шара равна площади сечения тела Т. Поэтому и объем половины шара равен объему этого тела. В свою очередь, объем тела Т можно вычислить как разность объемов цилиндра и конуса:

.

Итак, объем половины шара равен , следовательно, объем всего шара . Что и требовалось доказать.

Площадь сферы

Площадь сферы S радиуса R вычисляется по формуле .

Поделись с друзьями в социальных сетях:

Советуем посмотреть:

Предмет стереометрии

Параллельность и перпендикулярность прямых и плоскостей в пространстве

Многогранник

Призма

Параллелепипед

Объём тела

Свойства прямоугольного параллелепипеда

Пирамида

Цилиндр

Конус

Многогранники

Правило встречается в следующих упражнениях:

7 класс

Задание 1226, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 1228, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 1230, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 1231, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 23, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 24, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 26, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 1253, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 1254, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 1255, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

---

© budu5. com, 2021

Пользовательское соглашение

Copyright

ГБПОУ РК «Симферопольский колледж сферы обслуживания и дизайна»

Вся подробная информация по вопросам поступления в колледж и работе приемной комиссии находится во вкладке Абитуриенту и Приемная комиссия
ГБПОУ РК «Симферопольский колледж сферы обслуживания и дизайна» осуществляет прием документов в очном и электронном виде по адресу: 295015, Республика Крым,
г. Симферополь,ул. Севастопольская, 54. E-mail: [email protected]
Дни открытых дверей онлайн

«Горячая линия» по вопросам получения профессионального образования и профессионального обучения лиц с инвалидностью и лиц с ОВЗ, а также их последующего трудоустройства в Республике Крым, деятельности БПО

Просмотреть…

Абитуриенты, поступающие на специальность Технология парикмахерского искусства.
1. Последний день приема документов 10.08.2021г
2. Консультация по подготовке к вступительным испытаниям проводится 11.08.2021г.
в 9.00 по адресу : г Симферополь ул, Севастопольская 54.

Просмотреть сведения…

30 июня в ГБПОУ РК «Симферопольский колледж сферы обслуживания и дизайна» прошел выпускной

9 июня в колледже «Сервиса и дизайна» была проведена встреча с молодёжью на тему «Семейные ценности». Поговорили о выборе спутника жизни, что бы фундамент семьи был крепким, и о тех подводных камнях в семейной жизни с которыми сталкиваются все семейные пары, как все пережить и сохранить семью.

Читать дальше…

17 июня 2021 года начался Демонстрационный экзамен по стандартам Ворлдскиллс, который является формой государственной итоговой аттестации выпускников по программам среднего профессионального образования по профессиям 43. 01.09 Повар, кондитер и 29.01.05 Закройщик.
Демонстрационный экзамен по стандартам Ворлдскиллс Россия проводится с целью определения у обучающихся и выпускников уровня знаний, умений и навыков, позволяющих вести профессиональную деятельность в определенной сфере и (или) выполнять работу по конкретной профессии или специальности в соответствии со стандартами Ворлдскиллс Россия.

29.01.05 Закройщик

Администрация ГБПОУ РК «Симферопольский колледж сферы обслуживания и дизайна» поздравляет сотрудников, педагогический коллектив и обучающихся с праздником День России!

#участвуем
80- летние начала Великой отечественной войны
В рамках ежегодной акции “Красная гвоздика” Благотворительный фонд “ПАМЯТЬ ПОКОЛЕНИЙ” приготовил увлекательный квиз. Разгадай его сейчас и узнай новые и необычные факты о героях Великой Отечественной войны!
https://vk.com/wall-96665902_3534

01 июня 2021 года, во всемирный День защиты детей, волонтеры ГБПОУ РК «Симферопольский колледж сферы обслуживания и дизайна» приняли участие в сопровождении детей с особыми возможностями здоровья «Преград нет!» в Республике Крым. Спасибо волонтерам за работу!!!

Читать дальше…

Борьба с табачной зависимостью объединила много стран, и теперь каждый год 31 мая проходит Всемирный день без табака. Инициатором события стала Всемирная Организацией Здравоохранения (ВОЗ), которая активно борется с никотиновой зависимостью курящих людей. 31 мая 2021 года в колледже был проведен цикл мероприятий по данной теме: классные часы, беседы, акции .

Читать дальше…

17 мая 2021 года прошли соревнования по компетенции «Массажист» в рамках дополнительного этапа V Крымского чемпионата «Абилимпикс» — региональный этап VII Национального чемпионата по профессиональному мастерству среди инвалидов и лиц с ограниченными возможностями здоровья «Абилимпикс».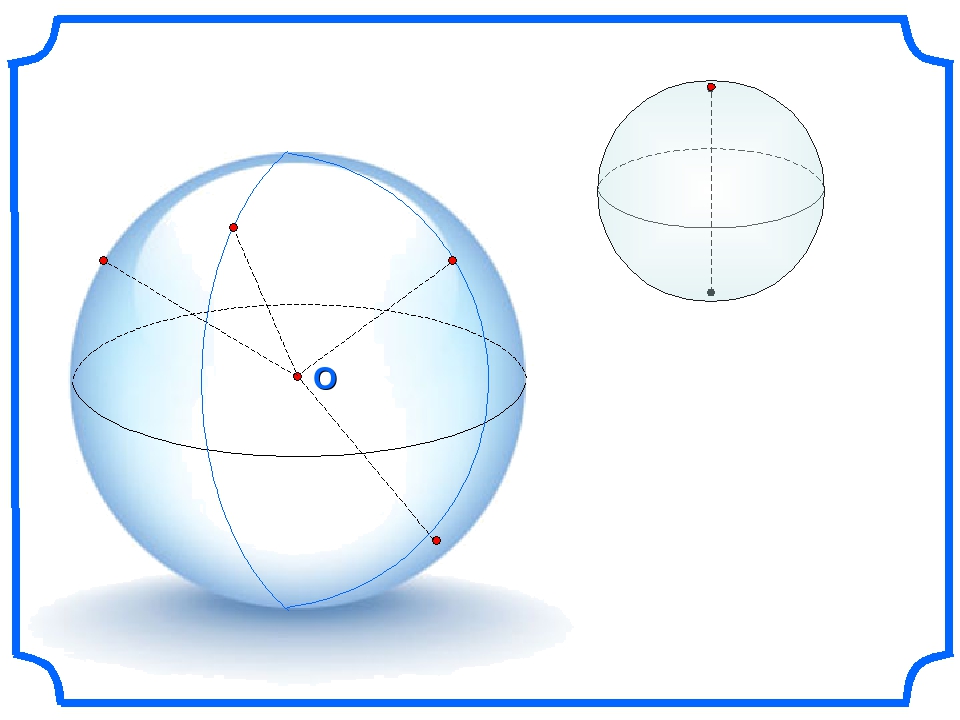

Читать дальше…

Региональный центр развития движения «Абилимпикс» в Республике Крым (ГБПОУ РК «Симферопольский колледж сферы обслуживания и дизайна») совместно с МБУ ДПО «Информационно- методический центр» муниципального образования городской округ Симферополь 28 апреля 2021 провели семинар- практикум для учителей технологии общеобразовательных учреждений г. Симферополя.

Читать дальше…

По давно сложившейся традиции в колледже каждую весну проходит предметная неделя для групп, обучающихся по профессиям «Закройщик», «Портной». Согласно плану, были подготовлены и проведены различные мероприятия для обучающихся, мастеров, преподавателей и приглашенных школьников.

Читать дальше…

Как рисовать шар карандашом поэтапно академический рисунок объемно

Овладеть основами рисунка должен любой художник, вне зависимости от жанра, в котором он намерен писать. Сначала надо научиться рисовать стандартные геометрические фигуры, только после этого переходить к более сложным конструкциям и портретам людей – лицевым и в полный рост.

Как нарисовать шар карандашом: последовательность действий

Уметь рисовать правильные шары необходимо для того, чтобы не испытывать затруднений при изображении объектов, в которых частично или полностью присутствует сферическая форма, к примеру, яблок, мячей, бутонов нераскрывшихся цветов.

При изображении трехмерных фигур большое внимание следует уделять светотени. Важно помнить, что от баланса света и тени будет зависеть, насколько объемно будет выглядеть объект на картинке. Резкие границы между светом и тенью подчеркивать не принято, но делать плавные переходы между ними надо.

Этапы рисования шара

Первым делом с помощью карандаша следует едва заметными линиями обозначить местоположение шара на бумаге. Затем перейти к созданию контура объекта при помощи внутренних эллипсов. Завершающей стадией будет моделирование света и тени и придание шару контраста.

Основа любого шара – это правильная окружность. Для ее изображения проводим две перпендикулярные линии. С четырех сторон от точки их пересечения обозначаем радиусы. На этом базисе рисуем окружность. Основа шара сделана, далее нужно придать ему объемный эффект. Выбираем место расположения источника света. От него к центру шара проводим линию, затем еще одну, перпендикулярная ей. На этих осях строим эллипс, одна полуокружность которого обозначит границу света и тени.

Затем от источника света к окружности проводим два касательных луча. Отмечаем точку соприкосновения шара с плоскостью, на которой он находится. Через нее и будет проходить ось падающей тени. На ней строим эллипс, который станет падающей тенью. Направленные от источника света касательные лучи на пересечении с осью укажут крайние точки эллипса. Тонируем все, что попадает в область тени как на поверхности шара, так и на плоскости, на которой он находится.

После этого добавляем тона падающей тени, поскольку это самая темная область. Усиливаем границу света и тени, чтобы она была яркой и контрастной. Затем распределяем тона внутри шара, при этом нижняя область должна быть темнее.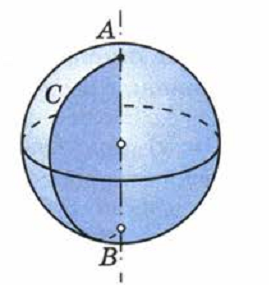 Для этого предварительно оставляем снизу сбоку с более освещенной стороны шара светлый полуэллипс — отражение света от лежащей рядом поверхности, а также блик – светлое пятно, где совершенно нет теней. Он должен быть там, куда под прямым углом падает свет. От блика должен расходится легкий тон, усиливающийся по мере удаления. Тонируем поверхность шара, делая плавный переход от светлых участков к темным. В завершение максимально тонируем падающую тень.

Учитесь рисовать шары

Умение рисовать шары необходимо всем, кто намерен серьезно заниматься изобразительным искусством. Навыки рисования других геометрических фигур также понадобятся на экзамене при поступлении в художественную академию.

Не расстраивайтесь, если что-то не получается. Мало кому удается нарисовать шар на отлично с первого раза. Для повышения мастерства необходима регулярная тренировка. Чтобы избежать проблем на экзаменах, придется нарисовать не один десяток шаров. Поэтому чем раньше начнете подготовку, тем увереннее будете себя чувствовать в самый ответственный момент.

В школе-студии К. Э. Арутюновой «Мастер рисунка» рисование различных фигур, в том числе шара, включено в обязательную программу курса. Занятия построены на принципе индивидуального подхода к каждому ученику с учетом его начального уровня подготовки, способностей, целей и сроков обучения. Наставник детально разбирает каждую работу ученика, указывает на погрешности и дает рекомендации для их исправления.

Чертеж шара и геометрия сферы формулы и рисунки

Чертеж шара и геометрия сферы формулы и рисунки, на которых показаны фигуры образованные путем пересечения различных плоскостей.

Всякое сечение сферы плоскостью есть круг. Большой круг имеет радиус R, который получается от сечения сферы с плоскостью, проходящей через ее центр.

Через всякие две точки сферы, не являющимися противоположными концами диаметра, всегда можно провести большой круг, и только один. Меньшая дуга этого большого круга является кратчайшим расстоянием на сфере между данными точками, соединяющая эти точки (так называемая геодезическая линия на сфере) и играет на поверхности ту же роль, что прямые на плоскости.

Геометрия сферы – это поверхность шара, которая характеризуется следующими величинами:

• D – диаметр шара;
  
• R – радиус шара;
  
• S – площадь (поверхность) сферы;
  
• V – объем шара
  

Размеры представленных величин определяются по формулам:

D = 2R

S = 4πR² = πD² ≈ 12,57R² ≈ 3,142D²

V = 4/3πR³ = πD³ /6 = 1/6√S3/π ≈ 0,5236D3 ≈ 0,09403√S³

R = ½ √S/π ≈ 0,2821√S

Шаровой сектор первого род – это фигура вращения сектора окружности относительно радиуса (первого рода),

S = πR(2h + a)

V = 2πR² h/3

Шаровой сектор второго род – это фигура вращения вокруг диаметра, не пересекающего его дуги (второго рода)

Шаровой сегмент – это часть шара, которая отсекается одной плоскостью

a² = h(2R – h)

S = π(2Rh + a²) = π(h² + 2a²)

V = 1/6 πh(3a² + h²) = 1/3 πh²(3R – h)

Шаровой слой – это часть шара, которая отсекается двумя параллельными плоскостями, расположенными на расстоянии h друг от друга

R² = a² + ((a² – b² – h²)/2h)²

S = π(2Rh + a² + b²)

V = 1/6 πh(3a² + 3b² + h²)

Справка:
Если V1 – объем усеченного конуса, вписанный в шаровой слой, и l – его образующая, то
V – V1 = 1/6πhl²

Заказать чертеж

Поделитесь с друзьями!

Подготовка школьников к ЕГЭ (Справочник по математике — Стереометрия

Шар, сфера и их части

      Введем следующие определения, связанные с шаром, сферой и их частями.

      Определение 1. Сферой с центром в точке   O   и радиусом   r   называют множество точек, расстояние от которых до точки   O   равно   r   (рис. 1).

      Определение 2. Шаром с центром в точке   O   и радиусом   r   называют множество точек, расстояние от которых до точки   O   не превосходит   r   (рис. 1).

Рис.1

      Таким образом, сфера с центром в точке   O   и радиусом   r   является поверхностью шара с центром в точке   O   и радиусом   r.

      Замечание. Радиусом сферы (радиусом шара) называют отрезок, соединяющий любую точку сферы с центром сферы. Длину этого отрезка также часто называют радиусом сферы (радиусом шара).

      Определение 3. Сферическим поясом (шаровым поясом) называют часть сферы, заключенную между двумя параллельными плоскостями параллельными плоскостями (рис. 2).

      Определение 4. Шаровым слоем называют часть шара, заключенную между двумя параллельными плоскостями параллельными плоскостями   (рис. 2).

Рис.2

      Окружности, ограничивающие сферический пояс, называют основаниями сферического пояса.

      Расстояние между плоскостями Расстояние между плоскостями оснований сферического пояса называют высотой сферического пояса.

      Из определений 3 и 4 следует, что шаровой слой ограничен сферическим поясом и двумя кругами, плоскости которых параллельны параллельны между собой. Эти круги называют основаниями шарового слоя.

      Высотой шарового слоя называют расстояние между плоскостями расстояние между плоскостями оснований шарового слоя.

      Определение 5. Сферическим сегментом называют каждую из двух частей, на которые делит сферу пересекающая ее плоскость (рис. 3).

      Определение 6. Шаровым сегментом называют каждую из двух частей, на которые делит шар пересекающая ее плоскость (рис. 3).

Рис.3

      Из определений 3 и 5 следут, что сферический сегмент представляет собой сферический пояс, у которого одна из плоскостей оснований касается сферы (рис. 4). Высоту такого сферического пояса и называют высотой сферического сегмента.

      Соответственно, шаровой сегмент – это шаровой слой, у которого одна из плоскостей оснований касается шара (рис. 4). Высоту такого шарового слоя называют высотой шарового сегмента.

Рис.4

      По той же причине всю сферу можно рассматривать как сферический пояс, у которого обе плоскости оснований касаются сферы (рис. 5). Соответственно, весь шар – это шаровой слой, у которого обе плоскости оснований касаются шара (рис. 5).

Рис.5

      Определение 7. Шаровым сектором называют фигуру, состоящую из всех отрезков, соединяющих точки сферического сегмента с центром сферы (рис.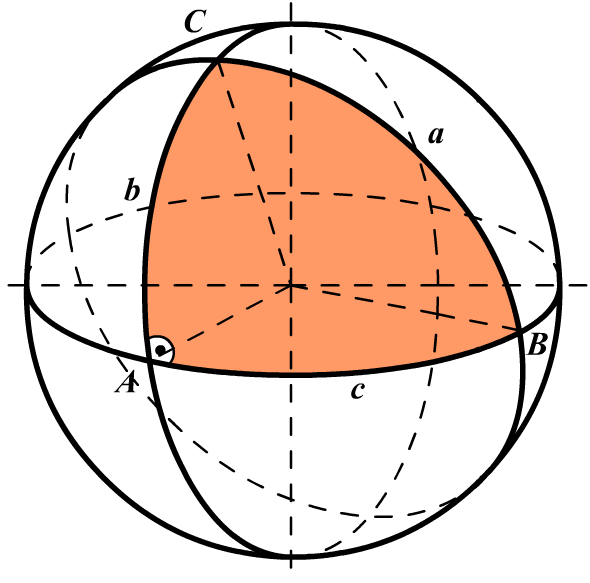 6).

Рис.6

      Высотой шарового сектора называют высоту его сферического сегмента.

      Замечание. Шаровой сектор состоит из шарового сегмента и конуса с общим основанием. Вершиной конуса является центр сферы.

Площади сферы и ее частей. Объемы шара и его частей

      В следующей таблице приведены формулы, позволяющие вычислить объем шара и объемы его частей, а также площадь сферы и площади ее частей.

      На нашем сайте можно также ознакомиться нашими учебными материалами для подготовки к ЕГЭ по математике.

Рисование сферических объектов — Карандашный рисунок

Помимо очевидных идеальных сфер, образующих структуру мяча — будь то гольф, теннис или баскетбол — есть объекты, которые имеют форму, основанную на сфере в той или иной форме. Яйцо, орех, яблоко и апельсин имеют видоизмененную сферу в качестве основной формы. Такие объекты, как миска, чашка и чайник, могут быть основаны на части сферы.

ВЫЛЕТОВ ИЗ ГЕОМЕТРИЧЕСКОЙ СФЕРЫ

Отклонения от геометрической сферы временами могут быть довольно радикальными, но все объекты на этих двух страницах основаны на ней.Например, в футболе сфера сужается с обоих концов; в кофеварке одна цельная сфера и две трети другой.

При рисовании любого структурно сферического объекта сначала нарисуйте всю сферу; затем добавьте требуемые выезды, которые требует ваш конкретный объект. Вы должны задать себе те же вопросы относительно пропорций, которые вы задавали при рисовании других форм. Насколько сильно ваш объект отклоняется — сглаживается, выпирает или изгибается — от геометрической сферы, которую вы сначала нарисовали как основу?

Соберите все сферические объекты, которые сможете найти, и нарисуйте их любого размера, который пожелаете.Но советуем рисовать довольно крупно, чтобы можно было свободно размахивать карандашом.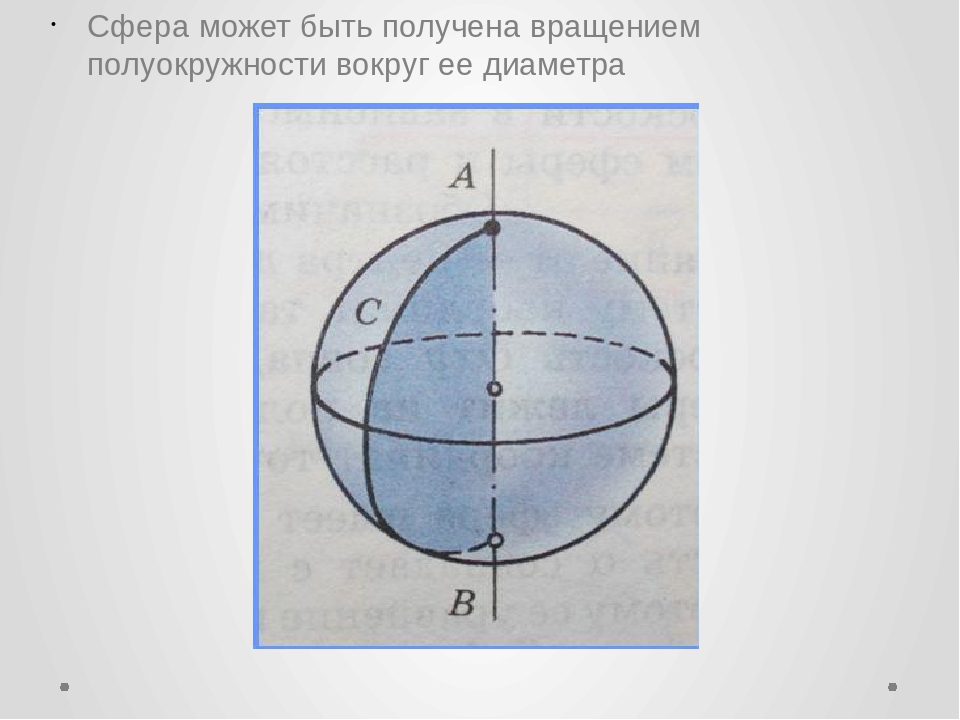

ГЛУБИНА И СФЕРА

Когда вы рисуете, помните, что сфера занимает заданное пространство; это не плоский диск. Возьмите яблоко или апельсин в руку и ощутите его объем. Постарайтесь передать этот объем и вес в своем рисунке. В следующих демонстрациях художник показал это трехмерное ощущение, используя эллипсы на яблоке и апельсине, а также на геометрических сферах, на которых они основаны.

Сфера является основной формой этого яйца и этого ореха. Помните, что сфера имеет три измерения. Эллипсы на форме яйца помогают подчеркнуть его глубину.

Несмотря на то, что каждый из этих объектов каким-то образом модифицирован, он основан на сфере. Обратите внимание на линию светлого карандаша через центр каждого объекта. Эта линия помогает художнику установить симметрию левой и правой сторон предметов.

Чайная чашка

1. Некоторые объекты имеют в своей структуре только часть сферы.Тем не менее, начните с рисования всей сферы, как показано пунктирной линией. Обратите внимание, как здесь эллипс художника определяет глубину сферы, придавая ей объем.

2. Теперь приступим к внесению изменений в сферу, которые могут превратить ее в чашку. Здесь художник опустил ломаную линию и работал только с нижней половиной сферы.

2. Теперь приступим к внесению изменений в сферу, которые могут превратить ее в чашку. Здесь художник опустил ломаную линию и работал только с нижней половиной сферы.

Яблоки и апельсины

1. С этими фруктами, как с любым фруктом, основанным на сфере, сначала нарисуйте законченную геометрическую сферу. Также нарисуйте эллипсы, чтобы определить третье измерение сферы — глубину.

2. После того, как основная форма установлена, вы можете добавить отклонения, которые делают ваш конкретный плод уникальным: его выпуклости, текстуру и стебель.

Читать здесь: Рисование конических объектов

Была ли эта статья полезной?

Как нарисовать сферу, которая выглядит идеально

Узнайте, как нарисовать сферу со всеми элементами, необходимыми для создания чего-то реалистичного. Нарисовать идеальную сферу с помощью карандаша может быть довольно сложно. Использовать векторную программу для этого относительно просто. Фактически, большинство приложений может помочь вам создать сферу, подобную приведенной ниже, всего за несколько секунд.

Есть несколько вещей, которые вы можете сделать, чтобы сделать вашу иллюстрацию более реалистичной. Я покажу вам несколько основных советов о том, как создать идеальную сферу, а также приведу несколько примеров изображений, которые не обязательно считаются идеальными сферами.

Простой круг, начинающийся с

Действительно, это нельзя считать шаром.На этой иллюстрации не видно ни теней, ни глубины, ни объема. Объект плоский, и все на этом изображении двухмерное. Давайте посмотрим, как можно легко смоделировать 3D-объект, используя только 2D-элементы.

Простая техника создания 3D-объекта

Самый простой способ создать 3D-объект, используя только 2D-формы, — это добавить подсветку круга, используя овальную форму, как показано ниже. Конечно, эффект довольно простой, и он может быть полезен только в том случае, если у вас нет доступа к инструменту градиентной заливки или вы просто хотите использовать этот конкретный стиль в своем проекте.

Использование инструмента градиентной заливки

Сначала это может показаться классной сферой. В конце концов, средние тона видны на всей иллюстрации, а нижняя часть объекта темнее, а верхняя — ярче. Однако эта сфера была создана с помощью инструмента градиентной заливки (что хорошо), но с использованием линейной заливки (что не очень хорошо).

Хотя результат отличный, трехмерный аспект этого изображения неточен. Чего-то не хватает для создания идеальной сферы, и требуется небольшая модификация, чтобы получить желаемый результат.

Вот идеальный шар!

Ниже вы можете увидеть идеальную сферу, также созданную с помощью инструмента градиентной заливки. На этот раз для создания этого классного изображения использовалась круглая заливка. Вот пять вещей, которые вам нужно увидеть в сфере, чтобы правильно проиллюстрировать этот объект:

1. Выделение: яркая и видимая область рядом с источником света (который расположен в правом верхнем углу иллюстрации). В этом случае центр блика почти полностью белый.
2. Средние тона: это область, где отраженный свет освещает объект. Вы должны увидеть идеальную градацию серых цветов, и эта градация должна быть круглой, чтобы добиться правильного эффекта.
3. Основная тень: Здесь находится самая темная часть сферы. Это очень важно, так как нам нужно, чтобы и светлые, и темные области были сильными, чтобы придать рисунку больше глубины и объема.
4. Отраженный свет: Небольшое дополнение, которое я сделал вручную. Вы видите тонкую яркую линию возле стрелки номер четыре? Это был бы свет, отраженный землей от объекта.
5. Отбрасываемая тень: в этом случае я сделал его ярче для удобства чтения, но не бойтесь создать темную отбрасываемую тень. Это важно для определения местоположения объекта в космосе.

Да, теперь вы знаете, как нарисовать реалистичную сферу!

При необходимости измените яркость, положение и цвет источника света. Как только вы начнете играть с этими элементами, возможности практически безграничны.

Как я уже сказал ранее, научиться рисовать сферу вручную возможно, но это может быть сложнее и труднее.Повеселись! 🙂

Вернуться к разделу «Научиться рисовать разные изображения с помощью векторного приложения»
Вернуться к разделу «Как рисовать сферу» на главную страницу

---

---

---

Как нарисовать сферу: пошаговое руководство

Научиться рисовать простые трехмерные фигуры, такие как кубы и сферы, — отличная практика для художников, желающих отточить свои навыки технического рисования. Если вы умеете набрасывать, рисовать и доводить до совершенства самые простые формы природы на бумаге, вы можете научиться рисовать что угодно с легкостью, конечно, с небольшой практикой.

В этом пошаговом руководстве мы научимся рисовать сферу, включая формирование идеального круга и правильную заливку.

Заявление об ограничении ответственности: Справочные изображения в этом руководстве взяты с PencilSessions. com, сайта, на котором размещены многочисленные руководства по рисованию фигур, животных и текстур.

В поисках идеального карандаша

Если вы какое-то время рисуете, вы, вероятно, знаете о системе классификации графита и нашли карандаш или карандаши, которыми вам удобнее всего рисовать.Если вы новичок в рисовании, графит классифицируется следующим образом:

Стандартный карандаш № 2 на этом графике будет считаться HB. Выбор карандаша зависит от вас, но примеры рисунков, используемых в этом руководстве, были нарисованы карандашами 3B-HB, поэтому, если вы хотите добиться того же тона, вы должны использовать их.

Более твердый графит обычно лучше всего подходит для быстрых эскизов, потому что он оставляет более светлые следы и его труднее размазать. Более мягкий графит лучше всего подходит для затенения, потому что он может стать очень темным и его легко размазать.

Как нарисовать сферу

Нарисованная сфера состоит из разных «частей» — всех продуктов освещения, которые вы пытаетесь имитировать на своем рисунке. Этими «частями» или «секциями» являются:

• Выделение: Выделение — это самая светлая часть вашей сферы, куда напрямую попадает источник света.
• Midtone: Midtone — это затенение в той части вашей сферы, куда свет не попадает напрямую. Он по-прежнему находится на линии прямой видимости источника света, но не настолько, чтобы быть таким же ярким, как блики.Это средний тон сферы.
• Core Shadow: Основная тень вашей сферы — это часть сферы, куда свет от вашего источника света вообще не попадает. Это самая темная часть сферы, прямо противоположная источнику света.

Прежде чем вы начнете рисовать, вам понадобится:

• Лист бумаги
• 3B-HB карандаши
• Ватные шарики или салфетки
• Что-то круглое для трассировки

Подождите, что это? След? Я знаю, я знаю, вы пытаетесь здесь научить рисовать.Однако, чтобы нарисовать идеальную сферу, вам нужно знать, как нарисовать идеальный круг, а это сложно. Чтобы овладеть навыками, требуется много практики и точности, поэтому, чтобы сэкономить время, просто потерпите меня и простите себя за этот короткий путь!

Конечно, если вы должны нарисовать свой собственный круг, никто вас не остановит. Больше возможностей для вас, если вам удастся нарисовать красивый с первой попытки! Впрочем, хватит подшучивания; Давайте начнем.

Шаг 1. Обведите круг

Возьмите что-нибудь круглое, например чашку или небольшую миску, положите на бумагу и начертите круг.

Это жульничество, да, но пока все в порядке. Причина, по которой мы учимся рисовать сферу, а не круг, заключается в том, что сфера должна быть правильно закрашена, и именно с этого начинается настоящее обучение.

Шаг 2 — Слегка заполните сферу

Очень, очень легко начните закрашивать сферу быстрыми, нежными движениями наброска. Определитесь с источником света и затените это пространство.

В этом примере источник света представлен стрелкой, и, как вы можете видеть на примере рисунка из Pencil Sessions, непосредственно перед источником света есть участок, который остается незатененным.

Шаг 3 — Сгладьте затенение кусочком хлопка или ткани

Пригладьте этот зернистый графитовый вид с помощью ватного диска или небольшого уголка ткани, чтобы ваша сфера выглядела более гладкой и светоотражающей. Будьте осторожны, чтобы не размазать графит слишком сильно за линии и не испачкать отражение источника света.

Шаг 4 — Затемните тени

Вернитесь к затенению сферы, на этот раз затемняя области, куда не попадает источник света.Это средний тон.

Шаг 5 — Сгладьте тени

Повторите процесс, начиная с шага 3. Используя ватный диск или уголок ткани, сгладьте зернистость только что добавленных теней, стараясь оставить светлые пятна там, где они должны быть.

Шаг 6 — Затемните внешние края

Снова заштрихуйте тени, на этот раз уделяя больше внимания внешним краям сферы напротив источника света и по обе стороны.

Шаг 7 — Сгладьте тени

Еще раз сгладьте зернистость недавно добавленных теней. Нам нужна максимально гладкая сфера!

Шаг 8 — Затемните сторону, противоположную источнику света

Затемните сферу сильнее, уделяя особое внимание границе круга напротив источника света. Используйте карандаш 3B, чтобы добавить темноты. Начните с умеренно темного цвета вдоль границы и разветвляйте тени в форме полумесяца.Корень этого затенения — это основная тень .

Источник света добавит сияющий, отражающий круг напротив ваших недавно добавленных теней, называемый светом. Представьте, что участок, который вы оставили незатененным, представляет собой идеальный круг, а вокруг него заштрихуйте полумесяцем. Внимательно изучите пример, и вы поймете, что я имею в виду.

Шаг 9 — Сгладьте тени

Если вам нужен гладкий оттенок с графитом, все зависит от хлопка и ткани! Сглаживайте свои новые добавления, как вы это делали раньше.

Шаг 10 — Очистите все!

Сотрите все пятна и следы линий, которые вышли за пределы вашей идеально заштрихованной сферы, стараясь не стереть ничего внутри вашего круга. После этого полюбуйтесь своим новым творением! (И спасибо Pencil Sessions за потрясающие пошаговые примеры рисунков.)

---

Вы сделали это! Чтобы получить больше советов по рисованию, рассмотрите возможность разветвления с курсом по технике рисования фигур или попробуйте свои силы в рисовании портретов.

Если фотореализм не для вас, подумайте о том, чтобы разработать свой собственный стиль рисования мультфильмов и научитесь рисовать карикатуры.

Страница Последнее обновление: Февраль 2020

Рисунок сферы — Как шаг за шагом нарисовать сферу

Рисование на бумаге по своей природе является 2D-носителем. Если вы не разбираетесь в цифровом программном обеспечении, вы никогда не получите настоящего трехмерного изображения на бумаге.

Тем не менее, есть уловки, которые можно использовать, чтобы получить что-то, имеющее вид 3D на плоской поверхности!

Одна из лучших форм, на которой можно это попробовать, — сфера, и здесь возникает вопрос: как научиться рисовать сферу на плоской бумаге?

Это пошаговое руководство о том, как нарисовать сферу за 6 шагов, покажет вам, как можно использовать освещение и тени для достижения максимально приближенного к 3D изображения на плоской поверхности .

Как нарисовать сферу — приступим!

Шаг 1

В этом руководстве о том, как нарисовать сферу, вы найдете несколько инструментов для рисования, которые будут очень полезны при завершении этого рисунка.

Вот мои РЕКОМЕНДУЕМЫЕ товары для творчества!

Во-первых, компас для рисования будет очень полезен, потому что чем ближе вы сможете подойти к идеальному кругу, тем лучше для этого рисунка.

Тогда вам понадобятся карандаши, по крайней мере, один светлый и один темный. Наконец, вам понадобится ластик хорошего качества.

По причинам, о которых мы поговорим позже, вам, вероятно, не следует использовать ручку для этого рисунка. С учетом всего сказанного, мы приступим к рисованию сферы прямо сейчас!

Для начала возьмите самый легкий карандаш и начертите круг с помощью циркуля. Если у вас нет циркуля для рисования, вы можете найти плоский объект, чтобы обвести его вокруг.

Крышка банки часто подходит для этого!

Постарайтесь сделать контур как можно более тонким и легким! Мы дали нам толстую линию для вашего удобства, но на вашем фото вы не должны видеть контура в конце.

Шаг 2 — Спланируйте источник света

Вот отличный совет для любого 3D-рисунка: главное в освещении. По этой причине мы будем рисовать в качестве ориентира, в каком направлении свет будет падать на ваш рисунок сферы.

С помощью светового карандаша вы можете нарисовать круг с отходящими от него линиями, чтобы создать источник света, падающий на вашу сферу.

Попытайтесь представить себе это как свет лампы, падающий на сферу, когда вы продвигаетесь вперед. Мы удалим эту ссылку позже, но она будет очень полезна, когда вы начнете добавлять тень.

Шаг 3. Теперь нарисуйте форму отбрасываемой тени

.

Один из способов передачи света и тени — это рисование отбрасываемой тени от объекта, поэтому мы спланируем это на этом шаге нашего руководства по рисованию сферы.

Световым карандашом нарисуйте плоский овал, отходящий от основания основной сферы.

Следуя как эталонному изображению, которое мы предоставили, так и изображению источника света, вы увидите, как он будет отражаться от сферы.

Попытайтесь нарисовать эту овальную направляющую очень легкими штрихами, так как позже вы не сможете увидеть контур тени.

Шаг 4 — Сотрите несколько линий на сфере для этого шага

В этой следующей части вашего рисования сферы вам нужно только стереть некоторые линии внутри сферы.

Осторожно сотрите любую часть овала теневого планирования внутри сферы. В нашем эталонном изображении мы также стерли изображение источника света, но я бы рекомендовал оставить его там немного дольше.

Шаг 5. Затем изобразите свой круг в виде шара

На этом пятом шаге нашего руководства о том, как нарисовать сферу, мы фактически ничего не будем рисовать.

Вместо этого вам следует обратиться к эталонному изображению, которое мы предоставили, чтобы помочь визуализировать, как будет выглядеть сфера.

Линии на контрольном изображении показывают, как бы выглядели изгибы мяча, если бы он не был плоским на странице.

Имея это в виду, вы готовы воплотить в жизнь 3D-эффект на следующем этапе!

Шаг 6 — Завершите 3D-эффект с помощью затенения

Последний шаг вашего рисования сферы — это то, где все это собрано вместе!

При раскрашивании сферы рекомендуется использовать карандаш или цветной карандаш, если вам нужны более яркие цвета.

При добавлении затенения старайтесь держать в уме эталонное изображение из шага 5, отраженный свет и тень.

Точка, в которой свет падает на сферу, будет самой яркой точкой на фигуре, и затемнение должно становиться темнее, чем дальше он попадает на другую сторону сферы.

Самой темной точкой будет отбрасываемая тень, когда она соединяется со сферой, и эта тень будет становиться немного светлее по мере удаления.

Все это может быть немного сложно и требует некоторой практики, но если вы будете следовать руководству и не торопиться, то вы определенно сможете это сделать!

Как только вы освоитесь, возможно, вы сможете начать использовать разные цвета и узоры, пытаясь сохранить трехмерный эффект.

Какие эффекты вы бы хотели добавить к своему изображению?

Рисунок вашей сферы завершен!

Это было довольно сложное руководство о том, как нарисовать сферу, поэтому вы должны быть особенно гордимся тем, что достигли конца этого урока!

Это может быть непросто, но, следуя этому руководству, надейтесь, что вы обнаружили, что рисование собственной 3D-сферы может быть проще, чем вы когда-либо думали!

Мы также надеемся, что вам было весело учиться вместе с нами в этом путешествии по рисованию.

Теперь, когда вы научились рисовать эту трехмерную сферу, вы также можете применить то, что вы узнали из этого руководства, к другим формам!

Если вы хотите, например, создать трехмерный куб или треугольник, просто вспомните, что вы узнали о отбрасывании света и тени.

У нас есть еще много интересного для вас на нашем сайте! У нас уже есть десятки путеводителей, и мы будем постоянно загружать их, чтобы вы могли наслаждаться ими!

Обязательно заходите почаще, чтобы познакомиться с новыми замечательными гидами.

Наконец, мы хотели бы увидеть ваш законченный рисунок сферы, поэтому обязательно поделитесь им на наших страницах в Facebook и Pinterest, чтобы мы могли ими восхищаться!

Как нарисовать сферу с помеченными тенями

Зачем рисовать сферу?

Вы можете спросить: «Зачем рисовать сферу?». В конце концов, в мире есть так много других интересных вещей, которые можно рисовать, кроме сферы.

В качестве упражнения рисуем сферу. Спортсмен много часов тренируется перед большой игрой.Художнику необходимо потренироваться и попрактиковаться, прежде чем браться за более сложные темы. Эти упражнения по рисованию помогают научить наш мозг видеть как художник и распознавать элементы, которые нам нужно решать в этих сложных предметах.

Две веские причины практиковать рисование сферой

Сфера — отличный предмет для отработки навыков рисования. Есть две важные причины, по которым сфера является таким замечательным предметом.

1. Сферы имеют полный диапазон значений — Значение — это темнота или яркость цвета.Этот важный элемент информирует зрителя о свете в сцене и форме объекта. Сфера, независимо от силы источника света, скорее всего, будет включать в себя полный спектр темных и светлых тонов.

Это означает, что вы, вероятно, увидите сверхтемные значения и значения света, а также много разных тонов между ними. Рисуя сферу, мы можем практиковаться в создании всего диапазона значений в нашем рисунке, уделяя пристальное внимание тонким изменениям тона.

2.Расположение ценностей легко распознать. — Важен не только полный диапазон значений, но и расположение этих ценностей не менее важно. Практикуя распознавание этих мест на сфере, мы лучше подготовлены к их поиску на более сложных предметах.

Расположение ценностей на сфере

Когда вы рисуете какой-либо объект, вы должны учитывать свой источник света. Свет внутри сцены определяет, где на объекте появятся ценные места. Помещая определенные значения в определенные места на нашем рисунке, мы можем сообщить зрителю о силе и расположении света.

Есть пять мест расположения ценностей, которые можно найти по любому предмету, но на сфере их легко распознать и они четко определены.

Выделение — Выделение — это место (я) более светлого оттенка на объекте, где свет падает с наибольшей интенсивностью.

Промежуточный тон — Промежуточный тон — это расположение среднего значения в теме. Обычно средний оттенок отражает местный цвет объекта.

Core Shadow — Основная тень — это наиболее темные участки на объекте.Эта тень находится на объекте, противоположном доминирующему источнику света.

Отраженный свет — Отраженный светлый свет является результатом попадания света на поверхность или окружающие объекты и отражения его обратно на объект в пределах или рядом с местом расположения основной тени.

Отбрасываемые тени — Отбрасываемые тени создаются на поверхности или окружающих объектах, когда свет не может попадать на эти поверхности, потому что объект блокирует свет.

Плавные градации значений

Еще одно преимущество практики со сферой — это возникающие градации значений.В отличие от куба или пирамиды, на сфере происходят постепенные изменения тона. Мы можем попрактиковаться в создании этих плавных и тонких переходов.

При использовании карандаша плавные переходы значений можно создавать небольшими круговыми штрихами. Этот прием часто называют «кружением». Мы также можем изменить направление штрихов, чтобы они текли по поперечным контурам формы. Комбинация обеих этих техник создает плавную градацию значений на наших рисунках.

Время практиковаться

Хотя убедительную сферу можно нарисовать без референса, часто лучше практиковаться по фотографии или живому объекту.Вместо того, чтобы придумывать расположение значений и тонов, мы можем их наблюдать. Рисование — это все, что нужно видеть.

Ниже вы найдете справочную фотографию, которую вы можете использовать, чтобы попрактиковаться в рисовании своей собственной сферы …

Путешествие и способ рисования сфер | Рефик Тюркели

(метод можно пролистать вниз)

После того, как я заинтересовался рисованием карандашом, мой друг познакомил меня с замечательной книгой Эндрю Лумиса под названием «Fun With A Pencil», чтобы помочь мне.

Книга начинается с представления о том, что можно нарисовать любую сложную фигуру из более простой. Например, вы можете начать рисовать голову, сначала нарисовав сферу. Затем вы можете добавить свои линии поверх этой сферы и создать окончательный рисунок.

Следующий шаг — нарисовать сферу. Сферу можно вращать с любой оси. Рисование сфер, повернутых по-разному, создало бы головы, смотрящие в разные стороны.

Примеры сфер Эндрю Лумиса

Я был удивлен, обнаружив, что ужасно представляю себе, как будут выглядеть линии на сфере после вращения.

Мой рисунок сферы

Так как мне нравится разбираться в вещах самостоятельно, я решил найти математику, лежащую в основе этих линий. Я подумал, что если я смогу разобраться в математике, у меня будет больше шансов их нарисовать.

Сначала я исследовал, что происходит с точкой A, когда сфера вращается вокруг оси X.

Это было легко. Чтобы узнать, насколько А переместится вверх, я посмотрел на сферу прямо с оси X.

Итак, если сфера поворачивается на α градусов вокруг оси X, точка A поднимется на sin (α) * r.

Рисовать и точно проверять мои выводы ручкой, бумагой и линейкой было очень утомительным занятием. Поэтому я решил написать для него программу. Казалось, что самый простой способ сделать это — использовать холст HTML5 и Javascript.

Холст HTML5 требует декартовых координат для точек рисования. Из-за моего краткого интереса к астрономии я знал более удобный способ определения точек на сферической поверхности. Так обращаются к звездам. Это делается с использованием двух углов: восхождения (а) и склонения (d).

Точка B может быть адресована этими двумя углами. Рассмотрим меридиан, проходящий из точки B. Вознесение (a) — это угол между этим меридианом и осью Z. Наклонение (d) — это угол между осью B и Y.

Допустим, вы хотите нарисовать меридиан, проходящий через B. Вы можете адресовать все точки на этом меридиане следующим образом: (восхождение: a, склонение: от 0 до 360).

Хотя я знал адреса точек с точки зрения восхождения и склонения, мне все же пришлось рисовать их на холсте.Мне нужен был способ преобразовать мои сферические координаты в декартовы координаты.

Сферические координаты в декартовы координаты

Теперь, когда я могу нарисовать любую точку на сфере, мне нужно было знать, как координаты изменятся после поворота. Мое первоначальное открытие sin (α) * r не было общей формулой, которую можно применить ко всем координатам.

Я решил, что если вращение выполняется по оси X, то компонент координат X не изменится. Это верно для любого вращения по любой оси. Исходя из этого понятия, я работал над вращением по оси Z.

Точка A имеет угол α с осью X. Он будет двигаться по круговой траектории, и конечный угол, который он будет иметь с осью X, будет α + β после β поворота по оси Z.

Это математика, лежащая в основе того, как любые новые значения координат могут быть вычислены после поворота β.

Моя программная сфера

После того, как все это было записано в код, все заработало замечательно. Вы можете поиграть с ним и прочитать код на этой странице.

Было приятно разобраться. Однако мне все еще нужен был практический способ рисования пером, так как я не могу производить все эти вычисления для каждого из моих рисунков.

Я начал с идеи, что любой рисунок сферы будет иметь вершину оси Z где-нибудь на окружности. Выбор этой точки на окружности означает выбор поворота сначала для оси Z, а затем для оси X.

Выбор точки для вершины оси Z также определяет вершину оси Y. Я искал практический способ определения положения оси Y с помощью оси Z.

Я могу определить «м», посмотрев на расстояние между центром круга и точкой, которую я выбрал для вершины оси Z.Что мне было нужно, так это практический способ определить «n», расстояние между краем круга и вершиной оси Y.

Под практическим я подразумеваю способ, не требующий вычислений. Поэтому я надеялся найти способ, который даст мне относительный ответ. Что-то вроде пропорции другой меры, которую я могу оценить своим глазом.

Я нашел «n» в терминах «m». Чтобы почувствовать это, я проигнорировал произведение «r» в конце уравнения и построил график для различных значений m / r.

График оказался кружком.Я чувствовал, что могу как-то этим воспользоваться. Вместо того, чтобы найти m / r на моем рисунке и подключить его к этому уравнению, я задумал кое-что попроще.

Поскольку уравнение для «n» имеет произведение «r» в конце, этот график станет идентичным кругу, который будет нарисован для сферы. Нарисовать касательную к этой окружности и сделать ее длину равной «m» — это то же самое, что вычислить m / r и вставить его в график. Это демонстрируется на шагах 3–6 разделов «Метод».

Нахождение «n» (CF) из «m» (AB) Путь оси Y во время вращения вокруг оси Z

Имея верхнюю часть осей Z и Y, Следующим изменением сферы может быть еще один поворот по оси Z.Это не изменит положение оси Z, но изменит положение оси Y. Верхняя часть оси Y будет перемещаться по эллипсу, и форма этого эллипса не изменится.

Чтобы создать этот вариант, я сначала нарисовал эллипс, проходящий через ось Y, а затем выбрал точку где-нибудь на нем. Это продемонстрировано на шагах 9–11 разделов «Метод».

Выбор точки для начала оси Y (J). Раньше это было в F.

Чтобы нарисовать остальную часть сферы, я наблюдал и записывал образцы вращающихся сфер в написанной мной программе.Линии для плоскостей XY, YZ и XZ после поворота становятся эллипсами на сфере. Мое главное наблюдение заключалось в том, что ось X делит YZ, ось Y делит XZ, а ось Z делит эллипсы плоскости XY от середины.

Центры всех эллипсов совпадают с центром круга. Я знал, что точки эллипса пересекаются с кругом, проведя перпендикулярную линию к линии оси, которая разделяет его посередине. Я также знал еще 2 точки на эллипсе, так как на нем находятся вершины осей. Этой информации достаточно для рисования эллипса.Пример находится на шаге 15 раздела «Метод».

Обзор метода

Метод, который я разработал на основе этих наблюдений, подробно объясняется ниже.

Как рисовать головы для идеальных пропорций лица

Научиться рисовать головы и пропорции рисования лиц — это одни из самых важных вещей, которым вы можете научиться как художник.

Существует несколько различных способов рисования этих основных пропорций лица, и это руководство будет следовать методу, описанному известным художником Эндрю Лумисом.

Нам нравится этот метод определения пропорций лица, потому что он прост для понимания и использует простые формулы, которые легко понять даже совершенно новым художникам.

Вот готовые направляющие для пропорций, которые вы научитесь создавать на следующих нескольких уроках.

Начать с кругов

Изучая, как рисовать головы, вы будете работать над изучением сразу всех различных видов головы.

И круг — это строительный блок, который будет двигать всем остальным. Пока вы рисуете круги, которые представляют собой плоские формы, помните, что голова имеет глубину, поэтому на следующем шаге вы превратите эти круги в сферы.

Превратите круги в сферы

Следующим шагом в обучении рисованию голов является рисование линий, разделяющих сферу на половинки. Вы можете легко нарисовать эти направляющие линии, потому что со временем вы их сотрете.

Вам нужно провести направляющую линию, которая проходит вокруг воображаемой средней точки следующих сторон сферы:

• Вертикально
• по горизонтали
• Из стороны в сторону

Можно подумать об этих направляющих линиях: если у вас есть апельсин, а затем вы разрезаете его пополам. Этот первый разрез будет горизонтальной средней линией.

Затем вы сделали еще один разрез апельсина, чтобы получить вертикальную среднюю линию. Наконец, последний разрез даст вам линию, которая проходит по бокам апельсина.В итоге у вас останется 8 одинаковых кусочков апельсина.

Это немного сложно объяснить словами, но если вы посмотрите на это изображение справа, я думаю, вы сразу поймете, как это работает.

Хитрость здесь в том, чтобы уметь извлекать эти ориентиры из головы, а это не самое легкое дело. Просто продолжайте практиковаться, и, если это поможет, вы можете даже взять апельсин или мяч для пинг-понга, а затем нарисовать направляющие линии, чтобы вы могли смотреть на него со всех сторон.

Помните, что ваше понимание объектов как имеющих глубину и размер всегда будет играть большую роль в том, чтобы то, что вы рисуете, казалось трехмерным, а не слишком плоским.

Сгладьте стороны сфер

В том месте, где в конечном итоге будут размещены уши, выровняйте стороны лица.