Рисовать симметрично: Рисование симметричных орнаментов в режиме симметрии

Опубликовано Автор Оставить комментарий

Содержание

Рисовать симметрично – как это — Воспитание и развитие ребенка — Родителям — Библиотека — ПочемуЧка

Рисовать симметрично — один из полезнейших прикладных навыков. Он нужен всем людям, которые много пишут и составляют таблицы, рисуют и чертят. В список профессий, где требуется умение создавать симметричные образы, входят инженер, математик, химик и физик, художник и архитектор, дизайнер, парикмахер и многие другие. Помимо этого, опыт симметричного рисунка незаменим для приобретения и развития красивого почерка.
 

Симметрия красива и приятна человеческому глазу, так как многое в природе живёт по канонам симметрии: листья на деревьях, лицо человека, тело животных, перья птиц. Часто симметрия используется в изобразительном искусстве. Этот прием добавляет в произведение гармоничность и сюжет. В музыке она используется в ритмах и кульминация, что особенно заметно при прослушивании классических музыкальных форм.

Стараясь рисовать симметрично, мозг активизирует те свои части, которые редко работают.

В этом есть неоспоримая польза для умственных способностей не только в масштабе сегодняшнего дня, но и в масштабе всей жизни. Известно, что люди, умеющие и учащиеся симметричному рисованию, намного реже болеют старческим слабоумием, ухудшением памяти и иными возрастными изменениями, связанными с редкой работой разных областей мозга.

Есть неисчислимое количество способов развития этого необходимого навыка, но все из них сводятся к банальной тренировке — взять в руки карандаш или ручку, положить перед собой лист и стараться повторять симметричные линии. Если одни специалисты советуют повторять вторую сторону своих же рисунков, другие в один голос заявляют о полезности перерисовывать сначала специально созданные для этого рисунки, а уже потом переходить к упражнениям с собственными.

Для полноценного развития этой техники следует тренироваться каждый день по 10-20 минут, постепенно увеличивая это время до 30 минут. Придерживаясь такого плана, Вы сможете научиться переносить одну часть рисунка на другую всего лишь за три-четыре недели. А если Вы хотите получить заветный навык в более короткий срок, то время ежедневной практики можно увеличить до часу, особенно полезно совмещать такие занятия с математическими упражнениями.

Рисовать, а тем более симметрично, полезно и интересно и для детей, и для взрослых. Такие тренировки для мозга равносильны зарядке для мышц. Научитесь Вы, и займитесь рисованием симметричных картинок с Вашими детьми. Это не только улучшит работу вашего мозга, но и сплотит семью.

5.10. Диалог «Симметричное рисование»

5.10. Диалог «Симметричное рисование»

5.10. Диалог «Симметричное рисование»

«Симметричное рисование» — это новая возможность для рисования в GIMP-2.10, поддерживаемая инструментами, использующими кисти («Карандаш», «Кисть», «Ластик», «Кисть MyPaint», «Клонирование», «Размазывание», «Осветление-затемнение»), а также инструментом «Перо». Есть несколько настраиваемых видов симметрии.

5.10.1. Вызов диалога

Получить доступ к этой команде можно с панели меню изображения: → →

Диалог «Симметричное рисование» является стыкуемым. Чтобы узнать больше о том, что такое стыкуемые диалоги, прочтите Раздел 2.3, «Диалоги и панели».

5.10.2. Работа с диалогом «Симметричное рисование»

Рисунок 15.85. Диалог «Симметричное рисование»

Это очень простой диалог с одним элементом Симметрия, который содержит выпадающий список с четырьмя возможностями. Сразу после того, как будет выбран тип симметрии, в окне изображения появляются оси симметрии в виде зелёных пунктирных линий, и можно начинать рисовать выбранной кистью.

Параметры

нет

Это значение по умолчанию; симметричное рисование отключено.

Зеркальная

Рисунок 15.86. Диалог зеркальной симметрии

Это симметрия подобна отражению в зеркале. Можно выбрать Горизонтальную симметрию, Вертикальную симметрию или Центральную симметрию. Также можно выбрать несколько типов симметрии.

Расположение по умолчанию для оси симметрии — середина окна изображения. С помощью параметров Позиция горизонтальной оси и Позиция вертикальной оси можно по желанию изменять местоположение осей.

Отключить преобразование кисти: во время преобразования рисунка кисть также будет в итоге преобразована. В зеркальном преобразовании, например, будет зеркально отображён не только рисунок с правой стороны холста на левую, но также и сама кисть очевидно «отображена» налево. Если по каким-то причинам нужно, чтобы зеркально отображались (или как-то по-другому трансформировались) рисуемые линии, но не сам контур кисти, то можно поставить галочку у этого параметра.

По очевидным причинам, для симметричных кистей этот параметр не показывается. Поэтому этот эффект часто не бывает виден, так как многие кисти являются симметричными.

Мозаичная

«Мозаика» — это симметрия переноса, которая может быть конечной (с максимальным числом штрихов) или бесконечной. В последнем случае это совершенный инструмент для создания текстур или бесшовных мозаик прямо во время рисования.

Рисунок 15.87. Диалог мозаичной симметрии

Этот режим касается изображений со штрихами

Осей здесь нет, но есть следующие параметры:

  • Интервал по XИнтервал по Y: интервалы по осям X и Y между центрами штрихов, в пикселях.

  • Смещение: смещение по линиям на оси X, в пикселях.

  • Макс. штрихов по оси X, Макс. штрихов по оси Y: максимальное число штрихов по осям X и Y. Значение по умолчанию — 0, что, согласно размеру изображения, означает «без ограничений».

Мандала

Рисунок 15.88. Диалог симметрии «Мандала»

Штрихи располагаются вокруг центра координат осей

Доступные параметры:

  • Абсцисса центра, Ордината центра для позиционирования центра координат.

  • Количество точек: число штрихов.

  • Отключить преобразование кисти: см. выше.

Выбрана кисть «перец», используется карандаш.

Пример для зеркальной симметрии

Рисунок 15.89. Вертикальная симметрия


Пример мозаики

Пример «Мандалы»

Симметрия для детей – симметрические фигуры и рисунки – Практические задания – Развитие ребенка

Симметрия и симметрические фигуры в математике 

Объяснить ребенку, что такое симметрия просто и наглядно достаточно легко, сложнее дать малышу понять, что являет собой симметрия в математике и зачем она в ней нужна.

Для обучения дошкольника основным принципам симметричного изображения фигур нужно проявить немного фантазии и учесть то, что дети дошкольного возраста лучше воспринимают мир наглядно, но, вместе с этим, быстро теряют интерес, если не понимают происходящее. Именно на устранении этих недочетах в обучении и построены основные схемы объяснения ребенку, что такое симметрические фигуры и как их изобразить на бумажном листе.

Изучаем зеркальную симметрию 

По своей природе, ребенок не может сразу изобразить две половинки одного целого одинаково. Рисунки маленьких детей почти всегда корявые и ассиметричные. Поэтому, когда мы изучаем зеркальную симметрию нужно объяснить ребенку, что половинки каждого из окружающих его предметов, как и собственное тело малыша, симметричны. Для подобного стартового этапа изучения симметрии подойдет упражнение с рисунком половины знакомого ребенку предмета красками впритык к сгибу альбомного листа и его перебивание на другую половину таким образом, чтоб получился целый предмет. Увидев результат полученной работы, объясните ребенку, что целый мячик, яблочко или что-либо изображенное, получилось из нарисованной половинки и есть отображение симметрии в предмете. Такие рисунки будут научным пособием для юного ученика о важности симметрии в окружающей его реальности.

Симметрия для детей

Другой разновидностью упражнений, которые входят в практические задания учимся рисовать симметрично являются упражнения, в которых мы с ребенком изучаем симметрию по точкам. Для формирования твердости руки и четкости движений ребенка, которые важны для четкого формирования рисунка попросите дошкольника соединить поставленные Вами точки в силуэт знакомого малышу предмета. Таким образом симметрия для детей станет более понятной и внедриться в реальный мир с помощью знакомых и интересных ребенку карандашей и красок.

Практические задания по симметрии 

Для облегчения обучения принципам одинаковости половинок рисунка можно распечатать симметрические рисунки для ребенка и проводить занятия по этим шаблонам. На нашем сайте подобраны одобренные педагогами детских центров раннего развития рисунки симметрии распечатать которые можно дома и дальше проводить занятия с включением этих дополнительных материалов. Материалы сайта Childdevelop характеризуются понятностью и доступностью для маленьких детей, учитывают особенности восприятия процесса обучения в детском возрасте и мелкой моторики. Практические задания по симметрии скачать бесплатно можно у нас и быстро получить от обучения результат, который порадует как школьными успехами, так и множеством красивых рисунков.

Как использовать Paint Symmetry в Photoshop CC 2019

Узнайте, как использовать новую функцию Paint Symmetry в Photoshop CC 2019, чтобы легко создавать забавные, симметричные рисунки и рисунки!

Симметрия рисования в Photoshop позволяет рисовать сразу несколько мазков кисти для создания зеркальных, симметричных рисунков и узоров. Он работает с Brush Tool, Pencil Tool и Eraser Tool, а также с масками слоев.

Впервые добавленная в качестве технического предварительного просмотра в Photoshop CC 2018, Paint Symmetry теперь является официальной частью Photoshop начиная с CC 2019. Все более основные параметры симметрии из CC 2018, такие как вертикальная, горизонтальная и диагональная, включены. Кроме того, CC 2019 также добавляет два новых режима симметрии, Radial и Mandala, которые позволяют создавать удивительные, очень сложные симметричные изображения за считанные секунды! Посмотрим, как это работает.

Чтобы следовать, вам понадобится Photoshop CC 2019 . И если вы уже являетесь подписчиком Creative Cloud, убедитесь, что ваша копия Photoshop CC обновлена . Давайте начнем!

Как рисовать с симметрией в фотошопе

Мы начнем с изучения основ того, как использовать Paint Symmetry для создания симметричных рисунков и дизайнов. Как только мы познакомимся с основами, я покажу вам, как комбинировать Paint Symmetry с масками слоев для более креативных эффектов!

Шаг 1: Добавьте новый пустой слой

Начните с добавления нового пустого слоя в ваш документ. Это будет держать ваши мазки кисти отдельно от всего остального. Чтобы добавить новый слой, щелкните значок « Новый слой» в нижней части панели «Слои» :

Нажав на иконку Новый слой.

Шаг 2. Выберите инструмент «Кисть», «Карандаш» или «Ластик».

Paint Symmetry работает с инструментами Brush Tool, Pencil Tool и Eraser Tool, которые находятся на панели инструментов . Я выберу инструмент Brush Tool :

Выбор инструмента «Кисть».

Как загрузить более 1000 кистей в Photoshop

Шаг 3: Откройте меню Paint Symmetry

При выбранном инструменте «Кисть», «Карандаш» или «Ластик» на панели параметров появляется значок «Симметрия краски» (маленькая бабочка). Нажмите на значок, чтобы открыть меню Paint Symmetry:

Нажав на значок симметрии краски (бабочка).

Шаг 4: Выберите опцию симметрии

А затем в меню выберите опцию симметрии из списка. В CC 2019 можно выбирать из десяти различных стилей, включая новые параметры Radial и Mandala внизу:

Параметры симметрии краски в Photoshop CC 2019.

Параметры «Симметрия краски» в Photoshop CC 2019

Вот краткий обзор того, как работает каждый из десяти параметров Photoshop Paint Symmetry:

  • Вертикальный: Делит холст вертикально и отражает мазки кисти с одной стороны на другую.
  • Горизонтально: Делит холст по горизонтали и отражает мазки кисти сверху вниз или снизу вверх.
  • Двойная ось: делит холст по вертикали и горизонтали на четыре равные части (вверху слева, вверху справа, внизу слева и внизу справа). Рисование в одном разделе отражает ваши мазки кистью в других трех.
  • Диагональ: Делит холст по диагонали и отражает мазки кисти с одной стороны на другую.
  • Волнистый: похож на вертикальный, но с изогнутой волнистой линией вместо прямой.
  • Круг: зеркально отображает мазки кисти, нарисованные внутри круга за пределами круга, и наоборот.
  • Спираль: зеркально отображает мазки кисти, нанесенные по обе стороны спиральной дорожки.
  • Параллельные линии: Делит холст на три вертикальных раздела, используя две параллельные вертикальные линии. Мазки кисти, нарисованные в средней части, отражаются в левой и правой частях.
  • Радиальный: Делит холст на диагональные сегменты или «кусочки». Мазки кистью, нарисованные в одном сегменте, отражаются в других.
  • Мандала: аналогично Radial, но также отражает мазки кисти в каждом сегменте, создавая в два раза больше мазков кисти, чем Radial.

Мы не будем здесь рассматривать все варианты симметрии, так как вы можете легко попробовать их самостоятельно. Но чтобы показать вам основы их работы, я выберу простую, например, Dual Axis . Двойная ось представляет собой комбинацию перечисленных выше вертикальных и горизонтальных режимов:

Выберите один из десяти вариантов Paint Symmetry.

Путь симметрии

Выбор параметра в меню добавляет синий путь симметрии к документу. В данном случае это путь симметрии Dual Axis, делящий холст по вертикали и горизонтали на четыре равные части:

Путь симметрии появляется.

Шаг 5: измените размер и примите путь

Прежде чем вы сможете рисовать с симметричной траекторией, Photoshop сначала помещает поле Transform вокруг пути, чтобы вы могли масштабировать и изменять его размер, если это необходимо. Но обратите внимание, что путь только для визуальной ссылки . Пути симметрии всегда влияют на весь холст, независимо от фактического размера пути. Поскольку рисование вне границы пути имеет тот же эффект, что и рисование внутри него, изменение размера симметрии на самом деле не дает никакой выгоды. Так что в большинстве случаев вам не нужно изменять его размер.

Однако, если вы хотите изменить размер пути, просто перетащите любой из маркеров преобразования, чтобы пропорционально масштабировать путь. Чтобы масштабировать путь от его центра, нажмите и удерживайте Alt (Победа) / Option (Mac) при перетаскивании ручки. Вы также можете переместить путь в другое место в документе, щелкнув и перетащив его в поле «Преобразование»:

Масштабирование пути симметрии путем перетаскивания угловой ручки.

Связанные: новые функции и изменения Free Transform в CC 2019

Чтобы принять путь (даже если вы не изменили его размер) и выйти из команды «Преобразовать», щелкните флажок на панели параметров или нажмите клавишу « Ввод» (Win) / « Return» (Mac) на клавиатуре:

Нажмите на галочку, чтобы зафиксировать путь.

Шаг 6: Нарисуйте в одном из разделов, чтобы создать симметрию

Затем, имея путь симметрии, просто нарисуйте внутри одного из разделов. Фотошоп автоматически скопирует и отразит ваш мазок кисти в других разделах, создав симметричный дизайн:

Рисование одного мазка кисти создает несколько зеркальных мазков.

Чем больше мазков кисти вы рисуете, тем сложнее становится дизайн.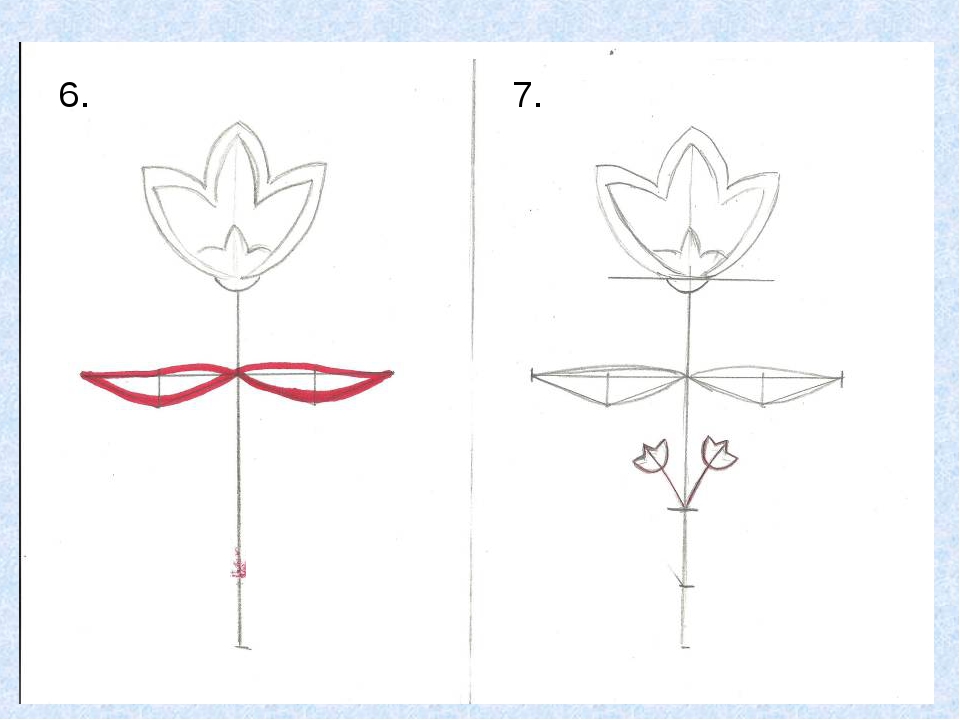 Даже имея ограниченные навыки рисования, Photoshop позволяет легко найти что-то интересное:

Картина более мазков кисти добавляет к симметричному дизайну.

Как скрыть путь симметрии

Чтобы просмотреть изображение, не мешая синему пути симметрии, спрячьте его, щелкнув значок Paint Symmetry (бабочка) на панели параметров и выбрав « Скрыть симметрию» :

Выбор «Скрыть симметрию» в параметрах «Симметрия краски».

Поскольку путь предназначен только для визуальной ссылки, вы можете продолжить рисовать и добавлять в дизайн даже со скрытым путем:

Сокрытие пути по-прежнему позволяет рисовать симметрично.

Как показать путь симметрии

Чтобы снова показать путь, щелкните значок бабочки на панели параметров и выберите « Показать симметрию» :

Выбор Показать симметрию из опций рисования симметрии.

И теперь путь снова виден:

Это искусство? Наверное, нет, но это было, конечно, легко.

Просмотр пути симметрии на панели «Пути»

Как и обычные контуры в Photoshop, контуры симметрии отображаются на панели «Контуры» . Путь именуется в зависимости от режима симметрии (в данном случае «Симметрия двойной оси 1»). И значок бабочки в правом нижнем углу эскиза говорит нам не только о том, что это путь симметрии, но и о том, что он в данный момент активен. Вы можете иметь несколько путей симметрии в одном документе (как мы увидим чуть позже), но одновременно может быть активен только один:

Пути симметрии можно просмотреть и выбрать на панели «Пути».

Новые опции радиальной и мандалевой симметрии

В Photoshop CC 2019 появилось два новых варианта Paint Symmetry — Radial и Mandala . Посмотрим, как они работают.

Как использовать параметр радиальной симметрии

Режим радиальной симметрии делит холст на диагональные сегменты или «кусочки» (например, кусочки пиццы). Картина в одном срезе отражает ваши мазки кистью в других.

Шаг 1: Выберите Radial из опций симметрии пути

Нажмите значок бабочки на панели параметров и выберите Радиальный из списка:

Выбор Radial из опций Paint Symmetry.

Шаг 2: Установите количество сегментов

Затем выберите нужное количество сегментов пути (срезов) от 2 до 12. Я пойду с 5:

Выбор количества сегментов, на которые нужно разделить холст.

Шаг 3: Нарисуйте в одном из сегментов

А потом просто нарисуйте в одном из сегментов. Photoshop будет отражать ваш мазок кисти в других сегментах, создавая радиальный рисунок:

Создание дизайна радиальной симметрии.

Как использовать опцию симметрии мандалы

Как и Radial, режим симметрии Mandala также делит холст на диагональные сегменты. Разница между Radial и Mandala заключается в том, что, наряду с отражением мазка кисти в других сегментах, Mandala также отражает штрих в том же сегменте. Это добавляет в два раза больше мазков кисти, чем Radial, что позволяет создавать очень сложные симметричные узоры с минимальными затратами времени и усилий.

Шаг 1: Выберите Mandala из опций симметрии пути

Нажмите значок бабочки на панели параметров и выберите Мандала из списка:

Выбор мандалы из опций Paint Symmetry.

Шаг 2: Установите количество сегментов

Затем, как и в Radial, выберите количество отрезков пути, которое вам нужно. В то время как Radial позволяет вам выбрать до 12 сегментов, Mandala ограничена до 10. Я пойду с 8:

Выбор количества сегментов.

Шаг 3: Нарисуйте в одном из сегментов

А затем, как и прежде, рисуйте в одном из сегментов. Photoshop будет отражать ваш мазок кисти в том же сегменте, в котором вы рисуете, и он будет отражать оба мазка кисти в других сегментах. Этот сложный дизайн занял у меня всего пару минут:

Мандала — самый впечатляющий (и забавный) из вариантов Photoshop’s Paint Symmetry.

Как отменить мазки кисти, если вы допустили ошибку

Создание симметричных рисунков в Photoshop — это весело и легко, но может потребовать много проб и ошибок. Если вам не нравится мазок кисти, который вы только что нарисовали, вы можете отменить его с клавиатуры, нажав Ctrl + Z (Победа) / Command + Z (Mac). Продолжайте нажимать на ярлык, чтобы отменить несколько мазков кисти. Чтобы повторить мазки кисти, нажмите Shift + Ctrl + Z (Победа) / Shift + Command + Z (Mac).

Как переключаться между путями симметрии

Photoshop позволяет нам добавить несколько путей симметрии к одному и тому же документу, и каждый из них будет добавлен на панель « Пути» . Значок бабочки в правом нижнем углу миниатюры указывает текущую активную путь симметрии. Только один путь может быть активным одновременно. В этом случае мой путь мандалы активен:

Значок бабочки показывает активный путь.

Чтобы переключиться на один из других путей в списке, щелкните правой кнопкой мыши (Win) / Control-click (Mac) на нужном пути:

Щелчок правой кнопкой мыши (Win) / Control-click (Mac) на пути радиальной симметрии.

И затем выберите Make Symmetry Path из меню:

Выбор команды «Создать путь симметрии».

Это деактивирует предыдущий путь и активирует новый, чтобы вы могли рисовать его в документе:

Путь радиальной симметрии теперь активен.

Параметр «Последняя использованная симметрия»

Вы также можете переключиться с текущего пути симметрии на ранее использовавшийся путь, щелкнув значок бабочки на панели параметров и выбрав « Последняя использованная симметрия» :

Путь радиальной симметрии теперь активен.

Как отключить Paint Symmetry

Чтобы отключить рисование симметрии и продолжить рисование без эффекта симметрии, щелкните значок бабочки на панели параметров и выберите « Выключить симметрию» :

Выбрав «Симметрия выкл» из меню.

Как использовать Paint Symmetry с маской слоя

Теперь, когда мы изучили основы работы Paint Symmetry, давайте посмотрим, как мы можем использовать путь симметрии с маской слоя, чтобы создать что-то еще более интересное.

В этом документе у меня есть радиальный градиент на фоновом слое:

Радиальный градиент спектра.

И если мы посмотрим на панель «Слои», то увидим, что у меня также есть сплошной черный слой над градиентом. Я включу верхний слой, щелкнув его значок видимости:

Включение верхнего слоя в документе.

И теперь документ заполнен черным, блокируя градиент из вида:

Верхний слой теперь скрывает градиент.

Шаг 1: Добавьте маску слоя

Выделив верхний слой, я добавлю маску слоя, щелкнув значок « Добавить маску слоя» в нижней части панели «Слои»:

Нажав значок Добавить маску слоя.

Эскиз маски слоя появляется на верхнем слое:

Эскиз маски слоя.

Шаг 2: Выберите инструмент Brush Tool

Я выберу инструмент Brush Tool на панели инструментов:

Выбор инструмента «Кисть».

Шаг 3: Установите цвет переднего плана на черный

И поскольку я хочу скрыть верхний слой в областях, где появляется эффект симметрии, я позабочусь о том, чтобы мой цвет переднего плана (цвет кисти) был установлен на черный :

Установка цвета кисти на черный.

Шаг 4: Выберите опцию Paint Symmetry

Я выберу мандалу из опций Paint Symmetry на панели параметров:

Выбор варианта симметрии.

А Photoshop добавляет путь симметрии мандалы к документу. Чтобы принять его, я нажму Enter (Win) / Return (Mac) на моей клавиатуре:

Путь симметрии добавляется в документ.

Шаг 5: Нарисуйте симметричный дизайн на маске слоя

Затем, чтобы скрыть текущий слой и показать слой под ним, просто нарисуйте маску слоя. Поскольку эффект симметрии расширяется, все больше и больше слоя ниже раскрывается. В этом случае цвета от моего градиента отображаются через мазки кисти:

Рисуем с симметричной траекторией на маске слоя, чтобы показать изображение ниже.

Я продолжу рисовать, чтобы добавить больше мазков к эффекту Мандала. И вот мой окончательный, красочный результат:

Окончательный дизайн мандалы.

И там у нас это есть! Вот как использовать Paint Symmetry в Photoshop CC 2019! Посетите наш раздел « Основы фотошопа » для получения дополнительных уроков! И не забывайте, что все наши учебники теперь доступны для скачивания в формате PDF !

Подписывайтесь на нашу новостную рассылку

Будьте первым, кто узнает, когда будут добавлены новые учебники!


Нарисовать симметричную фигуру относительно прямой.

Симметричное рисование предметов правильной формы

Цели:

  • образовательные:
    • дать представление о симметрии;
    • познакомить с основными видами симметрии на плоскости и в пространстве;
    • выработать прочные навыки построения симметричных фигур;
    • расширить представления об известных фигурах, познакомив со свойствами, связанных с симметрией;
    • показать возможности использования симметрии при решении различных задач;
    • закрепить полученные знания;
  • общеучебные:
    • научить настраивать себя на работу;
    • научить вести контроль за собой и соседом по парте;
    • научить оценивать себя и соседа по парте;
  • развивающие:
  • воспитательные:
    • воспитываать у учащихся “чувство плеча”;
    • воспитывать коммуникативность;
    • прививать культуру общения.

ХОД УРОКА

Перед каждым лежат ножницы и лист бумаги.

Задание 1 (3 мин).

– Возьмем лист бумаги, сложим его попалам и вырежем какую-нибудь фигурку. Теперь развернем лист и посмотрим на линию сгиба.

Вопрос: Какую функцию выполняет эта линия?

Предполагаемый ответ: Эта линия делит фигуру пополам.

Вопрос: Как расположены все точки фигуры на двух получившихся половинках?

Предполагаемый ответ: Все точки половинок находятся на равном расстоянии от линии сгиба и на одном уровне.

– Значит, линия сгиба делит фигурку пополам так, что 1 половинка является копией 2 половинки, т.е. эта линия непростая, она обладает замечательным свойством (все точки относительно ее находятся на одинаковом расстоянии), эта линия – ось симметрии.

Задание 2 (2 мин).

– Вырезать снежинку, найти ось симметрии, охарактеризовать ее.

Задание 3 (5 мин).

– Начертить в тетради окружность.

Вопрос: Определить, как проходит ось симметрии?

Предполагаемый ответ: По-разному.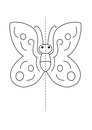

Вопрос: Так сколько осей симметрии имеет окружность?

Предполагаемый ответ: Много.

– Правильно, окружность имеет множество осей симметрии. Такой же замечательной фигурой является шар (пространственная фигура)

Вопрос: Какие еще фигуры имеют не одну ось симметрии?

Предполагаемый ответ: Квадрат, прямоугольник, равнобедренный и равносторонний треугольники.

– Рассмотрим объемные фигуры: куб, пирамиду, конус, цилиндр и т.д. Эти фигуры тоже имеют ось симметрии.Определите, сколько осей симметрии у квадрата, прямоугольника, равностороннего треугольника и у предложенных объемных фигур?

Раздаю учащимся половинки фигурок из пластилина.

Задание 4 (3 мин).

– Используя полученную информацию, долепить недостающую часть фигурки.

Примечание: фигурка может быть и плоскостной, и объемной. Важно, чтобы учащиеся определили, как проходит ось симметрии, и долепили недостающий элемент. Правильность выполнения определяет сосед по парте, оценивает, насколько правильно проделана работа.

Из шнурка одного цвета на рабочем столе выложена линия (замкнутая, незамкнутая, с самопересечением, без самопересечения).

Задание 5 (групповая работа 5 мин).

– Определить визуально ось симметрии и относительно нее достроить из шнурка другого цвета вторую часть.

Правильность выполненной работы определяется самими учениками.

Перед учащимися представлены элементы рисунков

Задание 6 (2 мин).

– Найдите симметричные части этих рисунков.

Для закрепления пройденного материала предлагаю следующие задания, предусмотренные на 15 мин.:

Назовите все равные элементы треугольника КОР и КОМ. Каков вид этих треугольников?

2. Начертите в тетради несколько равнобедренных треугольников с общим основанием равным 6 см.

3. Начертите отрезок АВ. Постройте прямую перпендикулярную отрезку АВ и проходящую через его середину. Отметьте на ней точки С и D так, чтобы четырехугольник АСВD был симметричен относительно прямой АВ.

– Наши первоначальные представления о форме относятся к очень отдаленной эпохе древнего каменного века – палеолита. В течение сотен тысячелетий этого периода люди жили в пещерах, в условиях мало отличавшихся от жизни животных. Люди изготовляли орудия для охоты и рыболовства, вырабатывали язык для общения друг с другом, а в эпоху позднего палеолита украшали свое существование, создавая произведения искусства, статуэтки и рисунки, в которых обнаруживается замечательное чувство формы.
Когда произошел переход от простого собирания пищи к активному ее производству, от охоты и рыболовства к земледелию, человечество вступает в новый каменный век, в неолит.
Человек неолита обладал острым чувством геометрической формы. Обжиг и раскраска глиняных сосудов, изготовление камышовых циновок, корзин, тканей, позже – обработка металлов вырабатывали представления о плоскостных и пространственных фигурах.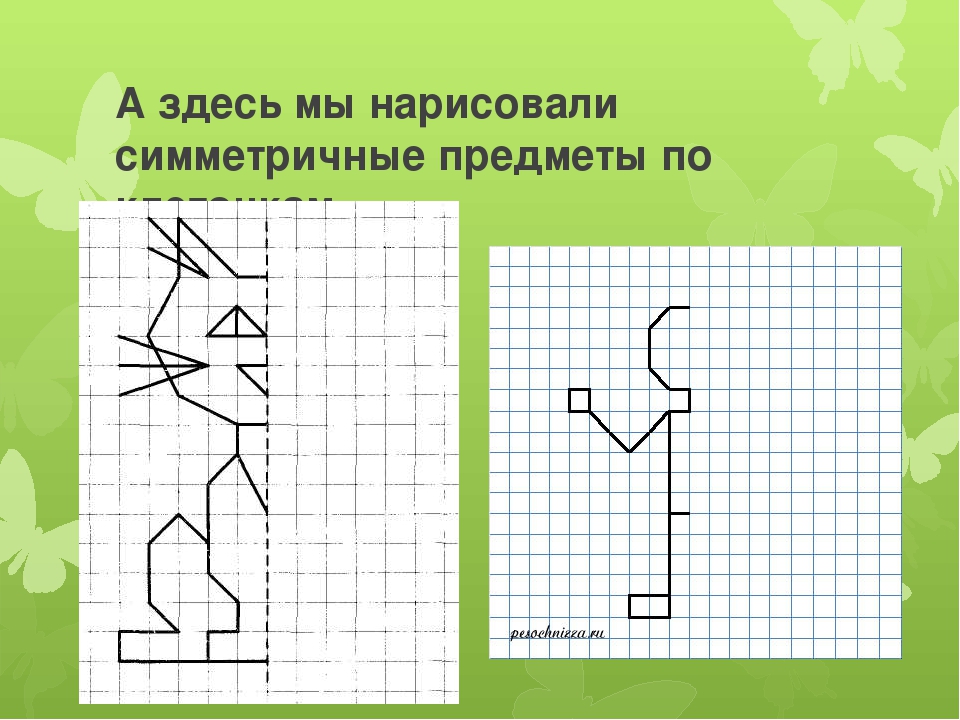 Неолитические орнаменты радовали глаз, выявляя равенство и симметрию.
– А где в природе встречается симметрия?

Предполагаемый ответ: крылья бабочек, жуков, листья деревьев…

– Симметрию можно наблюдать и в архитектуре. Строя здания, строители четко придерживаются симметрии.

Поэтому здания получаются такие красивые. Также примером симметрии служит человек, животные.

Задание на дом:

1. Придумать свой орнамент, изобразить его на листе формат А4 (можно нарисовать в виде ковра).
2. Нарисовать бабочек, отметить, где присутствуют элементы симметрии.

ТРЕУГОЛЬНИКИ.

§ 17. СИММЕТРИЯ ОТНОСИТЕЛЬНО ПРЯМОЙ.

1. Фигуры, симметричные друг другу.

Начертим на листе бумаги чернилами какую-нибудь фигуру, а карандашом вне её — произвольную прямую. Затем, не давая чернилам высохнуть, перегнём лист бумаги по этой прямой так, чтобы одна часть листа налегла на другую. На этой другой части листа получится, таким образом, отпечаток данной фигуры.

Если затем лист бумаги опять распрямить, то на нём окажутся две фигуры, которые называются симметричными относительно данной прямой (черт. 128).

Две фигуры называются симметричными относительно некоторой прямой, если при перегибании плоскости чертежа по этой прямой они совмещаются.

Прямая, относительно которой данные фигуры симметричны, называется их осью симметрии .

Из определения симметричных фигур следует, что всякие симметричные фигуры равны.

Получить симметричные фигуры можно и не пользуясь перегибанием плоскости, а с помощью геометрического построения. Пусть требуется построить точку С», симметричную данной точке С относительно прямой АВ. Опустим из точки С перпендикуляр
СD на прямую АВ и на продолжении его отложим отрезок DС» = DС. Если перегнём плоскость чертежа по АВ, то точка С совместится с точкой С»: точки С и С» симметричны (черт. 129).

Пусть требуется теперь построить отрезок С»D», симметричный данному отрезку СD относительно прямой АВ. Построим точки С» и D», симметричные точкам С и D. Если перегнём плоскость чертежа по АВ, то точки С и D совместятся соответственно с точками С» и D» (черт. 130).Поэтому отрезки СD и С»D» совместятся, они будут симметричны.

Построим теперь фигуру, симметричную данному многоугольнику АВСDЕ относительно данной оси симметрии МN (черт. 131).

Для решения этой задачи опустим перпендикуляры Аа , Вb , Сс , Dd и Ее на ось симметрии МN. Затем на продолжениях этих перпендикуляров отложим отрезки
а А» = Аа , b В» = Вb , с С» = Сс; d D»» =Dd и е Е» = Ее .

Многоугольник А»В»С»D»Е» будет симметричным многоугольнику АВСDЕ. Действительно, если перегнуть чертёж по прямой МN, то соответствующие вершины обоих многоугольников совместятся, а значит, совместятся и сами многоугольники; это и доказывает, что многоугольники АВСDЕ и А»В»С»D»Е» симметричны относительно прямой MN.

2. Фигуры, состоящие из симметричных частей.

Часто встречаются геометрические фигуры, которые какой-нибудь прямой разделяются на две симметричные части. Такие фигуры называются симметричными.

Так, например, угол — фигура симметричная, и биссектриса угла является его осью симметрии, так как при перегибании по ней одна часть угла совмещается с другой (черт. 132).

В круге осью симметрии является его диаметр, так как при перегибании по нему один полукруг совмещается с другим (черт. 133). Точно так же симметричны фигуры на чертежах 134, а, б.

Симметричные фигуры часто встречаются в природе, строительстве, в украшениях. Изображения, помещённые на чертежах 135 и 136, симметричны.

Следует заметить, что симметричные фигуры совместить простым передвижением по плоскости можно лишь в некоторых случаях. Чтобы совместить симметричные фигуры, как правило, необходимо одну из них повернуть обратной стороной,


  • Центральная симметрия
  • Осевая симметрия
  • Заключение

Определение

Симметрия (от греч. Symmetria – соразмерность), в широком смысле – неизменность структуры материального объекта относительно его преобразований. Симметрия играет огромную роль в искусстве и архитектуре. Но ее можно заметить и в музыке, и в поэзии. Симметрия широко встречается в природе, в особенности у кристаллов, у растений и животных. Симметрия может встретиться и в других разделах математики, например при построении графиков функций.


Центральная симметрия

Две точки А и А 1 называются симметричными относительно точки О , если О — середина отрезка АА 1. точка О считается симметричной самой себе.


Построение точки, центрально-симметричной данной

  • Построить луч АО
  • Измерить длину отрезка АО
  • Точка А1 симметрична точке А относительно центра О.

А 1


Построение отрезка, центрально-симметричного данному

  • Построить луч АО
  • Измерить длину отрезка АО
  • Отложить на луче АО по другую сторону от точки О отрезок ОА 1 , равный отрезку ОА.
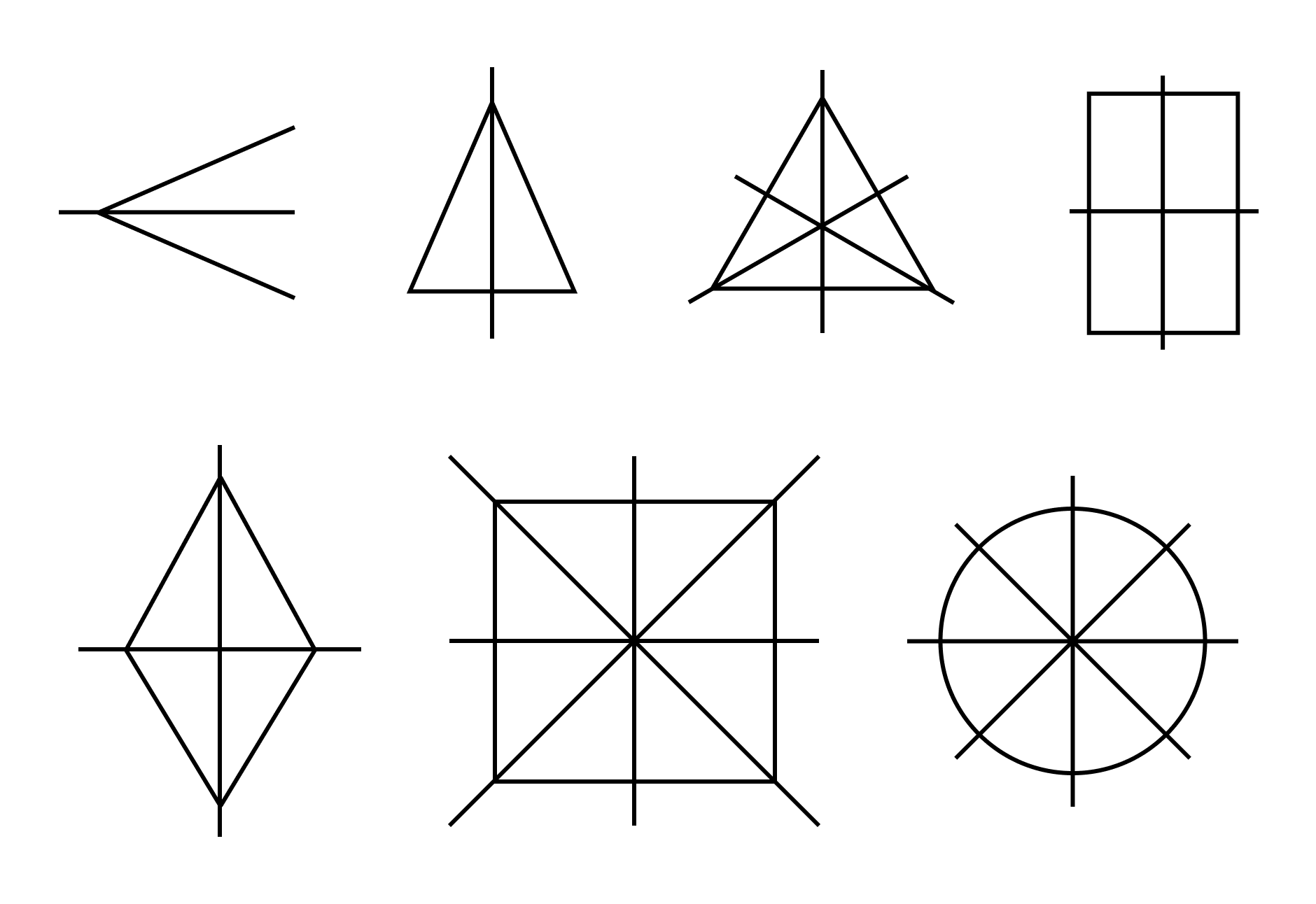
  • Построить луч ВО
  • Измерить длину отрезка ВО
  • Отложить на луче ВО по другую сторону от точки О отрезок ОВ 1 , равный отрезку ОВ.
  • Соединить точки А 1 и В 1 отрезком

А 1

В 1


А 1

С 1

В 1

Центрально-симметричные фигуры равны


Построение фигуры, центрально-симметричной данной


Поворот точки А вокруг центра поворота О на 90 °

А 1

90 °


Повороты точек на различные углы

А 1

135 °

45 °

А 2

90 °

А 3



Осевая симметрия

Преобразование фигуры F в фигуру F 1, при котором каждая ее точка переходит в точку, симметричную относительно данной прямой, называется преобразованием симметрии относительно прямой а . Прямая а называется осью симметрии.


Построение точки, симметричной данной

2. АО=ОА ’


Построение отрезка, симметричного данному

  • АА ’  с, АО=ОА ’ .
  • ВВ ’  с, ВО ’ =О ’ В ’ .

3. А ’ В ’ – искомый отрезок.


Построение треугольника, симметричного данному

1. AA’  c AO=OA’

2. BB’  c BO’=O’B’

3. СС ’  c С O”=O” С ’

4.  A’B’ С ’ – искомый треугольник.


Построение фигуры, симметричной данной относительно оси симметрии


Фигуры, обладающие одной осью симметрии

Угол

Равнобедренный

треугольник

Равнобедренная трапеция


Фигуры, обладающие двумя осями симметрии

Прямоугольник

Ромб


Фигуры, имеющие более двух осей симметрии

Квадрат

Равносторонний треугольник

Круг


Фигуры, не обладающие осевой симметрией

Произвольный треугольник

Параллелограмм

Неправильный многоугольник



«Симметрия является той идеей, посредством которой человек на протяжении веков пытался постичь и создать порядок, красоту и совершенство»

Если на минутку задуматься и представить у себя в воображении какой-либо предмет, то в 99% случаев фигура, пришедшая на ум, будет правильной формы.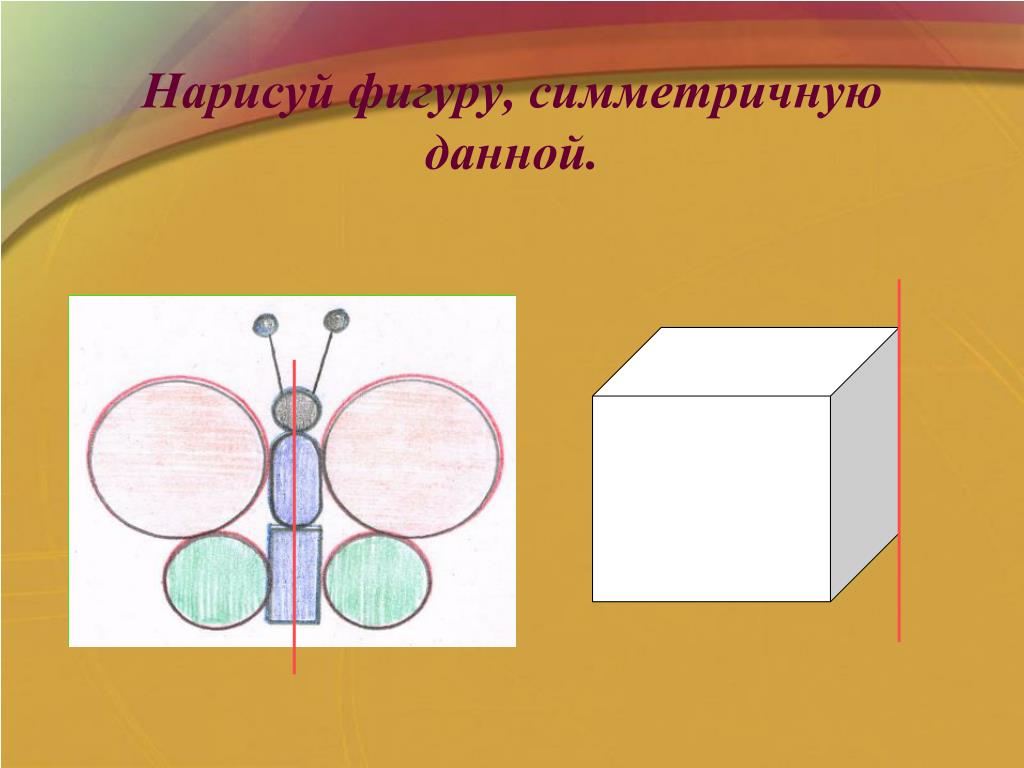 Лишь 1 % людей, точнее их воображение, нарисует замысловатый объект, выглядящий совсем неправильно или непропорционально. Это скорее исключение из правил и относится к нетрадиционно размышляющим личностям с особым взглядом на вещи. Но возвращаясь к абсолютному большинству, стоит сказать, что существенная доля правильных предметов все же преобладает. В статье пойдет речь исключительно о них, а именно о симметричном рисовании таковых.

Изображение правильных предметов: всего несколько шагов до законченного рисунка

Прежде чем приступить к рисованию симметричного предмета, нужно его выбрать. В нашем варианте это будет ваза, но даже если она никак не напоминает то, что решили изображать вы, не отчаивайтесь: все шаги абсолютно идентичны. Придерживайтесь последовательности и все получится:

  1. У всех предметов правильной формы есть так называемая центральная ось, которую при симметричном рисовании обязательно стоит выделить. Для этого можно даже воспользоваться линейкой и провести по центру альбомного листа прямую линию.
  2. Далее внимательно посмотрите на выбранный вами предмет и постарайтесь перенести его пропорции на лист бумаги. Сделать это несложно, если с обеих сторон проведенной заранее линии, наметить легкие штрихи, которые впоследствии станут очертаниями рисуемого предмета. В случае с вазой необходимо выделить горлышко, донышко и самую широкую часть корпуса.
  3. Не забывайте о том, что симметричное рисование не терпит неточностей, поэтому если есть некоторые сомнения относительно намеченных штрихов, или вы не уверены в правильности собственного глазомера, перепроверьте отложенные расстояния при помощи линейки.
  4. Последний шаг — соединение всех линий воедино.

Симметричное рисование доступно компьютерным пользователям

В силу того что большинство окружающих нас предметов имеют правильные пропорции, иначе говоря симметричны, разработчики компьютерных приложений создали программы, в которых легко можно нарисовать абсолютно все. Достаточно лишь скачать их и наслаждаться творческим процессом.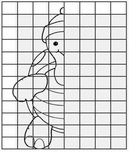 Однако помните, машина никогда не станет заменой остро наточенному карандашу и альбомному листу.

I . Симметрия в математике :

    Основные понятия и определения.

    Осевая симметрия (определения, план построения, примеры)

    Центральная симметрия (определения, план построения, при ­меры)

    Обобщающая таблица (все свойства, особенности)

II . Применения симметрии:

1) в математике

2) в химии

3) в биологии, ботанике и зоологии

4) в искусстве, литературе и архитектуре

1. Основные понятия симметрии и ее виды.

Понятие симметрии пр оходит через всю историю человечества. Оно встречается уже у истоков человеческого знания. Возникло оно в связи с изучением живого ор­ганизма, а именно человека. И употреблялось скульпторами ещё в 5 веке до н. э. Слово “симметрия” греческое, оно означает “соразмерность, пропорциональность, одинаковость в расположении частей”. Его широко используют все без исключения направления современной науки. Об этой закономерности задумывались многие ве­ликие люди. Например, Л. Н. Толстой говорил: “Стоя перед черной доской и рисуя на ней мелом разные фигуры, я вдруг был поражен мыслью: почему симметрия по­нятна глазу? Что такое симметрия? Это врожденное чувство, отвечал я сам себе. На чем же оно основано?”. Действительно симметричность приятна глазу. Кто не любо­вался симметричностью творений природы: листьями, цветами, птицами, живот­ными; или творениями человека: зданиями, техникой, – всем тем, что нас с детства окружает, тем, что стремится к красоте и гармонии. Герман Вейль сказал: “Симмет­рия является той идеей, посредством которой человек на протяжении веков пытался постичь и создать порядок, красоту и совершенство”. Герман Вейль – это немецкий математик. Его деятельность приходится на первую половину ХХ века. Именно он сформулировал определение симметрии, установил по каким признакам усмотреть наличие или, наоборот, отсутствие симметрии в том или ином случае. Таким обра­зом, математически строгое представление сформировалось сравнительно недавно – в начале ХХ века. Оно достаточно сложное. Мы же обратимся и еще раз вспомним те определения, которые даны нам в учебнике.

2. Осевая симметрия.

2.1 Основные определения

Определение. Две точки А и А 1 называются симметричными относительно прямой а, если эта прямая проходит через середину отрезка АА 1 и перпендику­лярна к нему. Каждая точка прямой а считается симметричной самой себе.

Определение. Фигура называется симметричной относительно прямой а , если для каждой точки фигуры симметричная ей точка относительно прямой а также принадлежит этой фигуре. Прямая а называется осью симмет­рии фигуры. Говорят также, что фигура обладает осевой симметрией.

2.2 План построения

И так, для построения симметричной фигуры относительно прямой от каждой точки проводим перпендикуляр к данной прямой и продлеваем его на такое же рас­стояние, отмечаем полученную точку. Так поступаем с каждой точкой, получаем симметричные вершины новой фигуры. Затем последовательно их соединяем и по­лучаем симметричную фигуру данной относительной оси.

2.3 Примеры фигур, обладающих осевой симметрией.


3. Центральная симметрия

3.1 Основные определения

Определение . Две точки А и А 1 называются симметричными относительно точки О, если О — середина отрезка АА 1 . Точка О считается симметричной са­мой себе.

Определение. Фигура называется симметричной относительно точки О, если для каждой точки фигуры симметричная ей точка относительно точки О также принадлежит этой фигуре.

3.2 План построения

Построение треугольника симметричного данному относительно цен­тра О.

Чтобы построить точку, симметричную точке А относи­тельно точки О , достаточно провести прямую ОА (рис. 46) и по другую сторону от точки О от­ложить отрезок, равный отрезку ОА .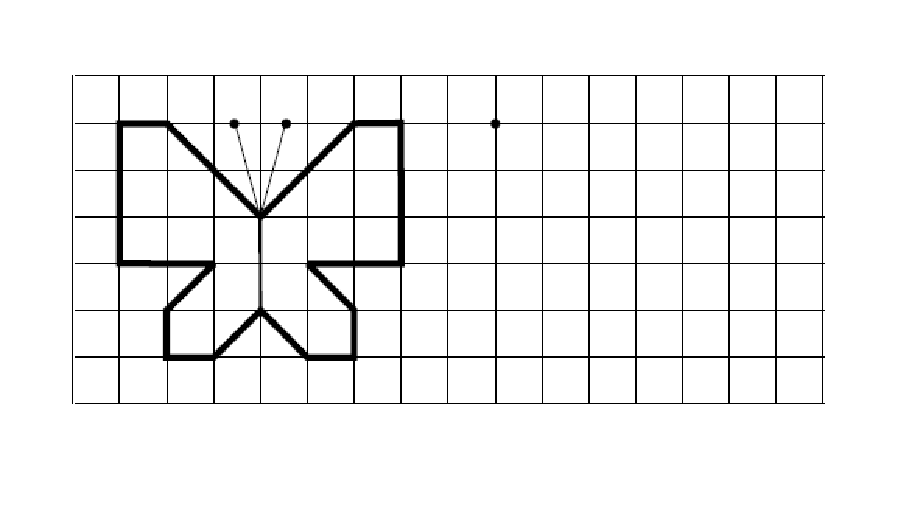 Иными словами, точки А и ; В и ; С и симметричны относительно некоторой точки О. На рис. 46 по­строен треугольник, симметричный треуголь­нику ABC относительно точки О. Эти треугольники равны.

Построение симметричных точек относительно центра.

На рисунке точки М и М 1 , N и N 1 симметричны относительно точки О, а точки Р и Q не симметричны относительно этой точки.

Вообще фигуры, симметричные относительно некоторой точки, равны.

3.3 Примеры

Приведём примеры фигур, обладающие центральной симметрией. Простейшими фигурами, обладающими центральной симметрией, является окружность и паралле­лограмм.

Точка О называется центром симметрии фигуры. В подобных случаях фигура обладает центральной симметрией. Центром симметрии окружности является центр окружности, а центром симметрии параллелограмма- точка пересечения его диаго­налей.

Прямая также обладает центральной симметрией, однако в отличие от окруж­ности и параллелограмма, которые имеют только один центр симметрии (точка О на рисунке) у прямой их бесконечно много — любая точка прямой является её центром симметрии.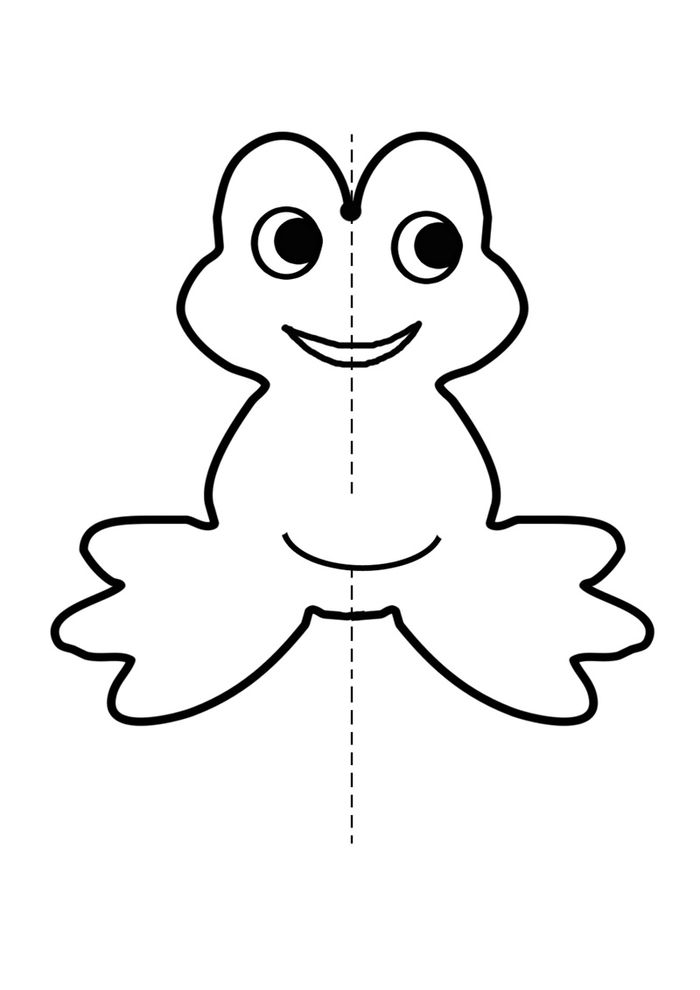

На рисунках показан угол симметричный относительно вершины, отрезок сим­метричный другому отрезку относительно центра А и четырехугольник симметрич­ный относительно своей вершины М.

Примером фигуры, не имеющей центра симметрии, является треугольник.

4. Итог урока

Обобщим полученные знания. Сегодня на уроке мы познакомились с двумя основ­ными видами симметрии: центральная и осевая. Посмотрим на экран и системати­зируем полученные знания.

Обобщающая таблица

Осевая симметрия

Центральная симметрия

Особенность

Все точки фигуры должны быть симметричны относительно какой-нибудь прямой.

Все точки фигуры должны, сим­метричны относительно точки, вы­бранной в качестве центра симмет­рии.

Свойства

    1. Симметричные точки лежат на перпендикулярах к прямой.

    3. Прямые переходят в прямые, углы в равные углы.

    4. Сохраняются размеры и формы фигур.

    1. Симметричные точки лежат на прямой, проходящей через центр и данную точку фигуры.

    2. Расстояние от точки до прямой равно расстоянию от прямой до симметричной точки.

3. Сохраняются размеры и формы фигур.

II. Применение симметрии

Математика

На уроках алгебры мы изу­чили графики функций y=x и y=x

На рисунках представлены различные картинки, изо­браженные с помощью вет­вей парабол.

(а) Октаэдр,

(б) ромбический додекаэдр, (в) гексагональной октаэдр.

Русский язык

Печатные буквы русского алфавита тоже обладают различными видами сим­метрий.

В русском языке есть «сим­метричные» слова — палин­дромы , которые можно чи­тать одинаково в двух на­правлениях.

А Д Л М П Т Ф Ш – вертикальная ось

В Е З К С Э Ю — горизонтальная ось

Ж Н О Х — и вертикальная и горизонтальная

Б Г И Й Р У Ц Ч Щ Я – ни какой оси

Радар шалаш Алла Анна

Литература

Могут быть палиндромичес- кими и предложения. Брюсов написал стихотворение «Голос луны», в котором каждая строка — палиндром.

Посмотрите на четверости -шие А.С.Пушкина «Медный всадник». Если провести ли­нию после второй строчки мы можем заметить эле­менты осевой симметрии

А роза упала на лапу Азора.

Я иду с мечем судия. (Державин)

«Искать такси»

«Аргентина манит негра»,

«Ценит негра аргентинец»,

«Леша на полке клопа нашел».

В гранит оделася Нева;

Мосты повисли над водами;

Темно-зелеными садами

Ее покрылись острова…

Биология

Тело человека построено по принципу двусторонней симметрии. Большинство из нас рассматривает мозг как единую структуру, в дейст­вительности он разделён на две половины. Эти две части — два полушария — плотно прилегают друг к другу. В полном соответст­вии с общей симметрией тела человека каждое по­лушарие представляет со­бой почти точное зеркаль­ное отображение другого

Управление основными движениями тела человека и его сенсорными функ­циями равномерно распре­делено между двумя полу­шариями мозга. Левое по­лушарие контролирует пра­вую сторону мозга, а правое — левую сторону.

Ботаника

Цветок считается симмет­ричным, когда каждый око­лоцветник состоит из рав­ного числа частей. Цветки, имея парные части, счита­ются цветками с двойной симметрией и т.д. Тройная симметрия обычна для од­нодольных растений, пя­терная — для двудольных Характерной чертой строе­ния растений и их развития является спиральность.

Обратите внимание на по­беги листорасположения – это тоже своеобразный вид спирали – винтовая. Еще Гёте, который был не только великим поэтом, но и естествоиспытателем, считал спиральность одним из характерных признаков всех организмов, проявле­нием самой сокровенной сущности жизни. Спи­рально закручиваются усики растений, по спирали происходит рост тканей в стволах деревьев, по спи­рали расположены семечки в подсолнечнике, спираль­ные движения наблюда­ются при росте корней и побегов.

Характерной чертой строения растений и их раз­вития является спиральность.

Посмотрите на сосновую шишку. Чешуйки на ее поверхности расположены строго закономерно — по двум спиралям, которые пересекаются приблизительно под прямым углом. Число таких спиралей у сосновых шишек равно 8 и 13 или 13 и 21.


Зоология

Под симметрией у живот­ных понимают соответствие в размерах, форме и очерта­ниях, а также относительное расположение частей тела, находящихся на противопо­ложных сторонах разде­ляющей линии. При ради­альной или лучистой сим­метрии тело имеет форму короткого или длинного ци­линдра либо сосуда с цен­тральной осью, от которого отходят в радиальном по­рядке части тела. Это ки­шечнополостные, иглоко­жие, морские звёзды. При билатеральной симметрии осей симметрии три, но симметричных сторон только одна пара. Потому что две другие стороны — брюшная и спинная — друг на друга не похожи. Этот вид симметрии характерен для большинства животных, в том числе насекомых, рыб, земноводных, рептилий, птиц, млекопитающих.

Осевая симметрия


Различные виды симметрии физических явлений: сим­метрия электрического и магнитного полей (рис. 1)

Во взаимно перпендику­лярных плоскостях симмет­рично распространение электромагнитных волн (рис. 2)


рис.1 рис.2

Искусство

В произведениях искусства часто можно наблюдать зеркальную симметрию. Зеркальная» симметрия ши­роко встречается в произве­дениях искусства прими­тивных цивилизаций и в древней живописи. Средне­вековые религиозные кар­тины также характеризу­ются этим видом симмет­рии.

Одно из лучших ранних произведений Рафаэля – «Обручение Марии» — соз­дано в 1504 году. Под сол­нечным голубым небом раскинулась долина, увен­чанная белокаменным хра­мом. На первом плане – об­ряд обручения. Первосвя­щенник сближает руки Ма­рии и Иосифа. За Марией – группа девушек, за Иоси­фом – юношей. Обе части симметричной композиции скреплены встречным дви­жением персонажей. На со­временный вкус компози­ция такой картины скучна, поскольку симметрия слишком очевидна.



Химия

Молекула воды имеет плос­кость симметрии (прямая вертикальная линия).Ис­ключительно важную роль в мире живой природы иг­рают молекулы ДНК (де­зоксирибонуклеиновая ки­слота). Это двуцепочечный высокомолекулярный по­лимер, мономером которого являются нуклеотиды. Мо­лекулы ДНК имеют струк­туру двойной спирали, по­строенной по принципу комплементарности.

Архите ктура

Издавна человек использо­вал симметрию в архитек­туре. Особенно блиста­тельно использовали сим­метрию в архитектурных сооружениях древние зод­чие. Причем древнегрече­ские архитекторы были убеждены, что в своих про­изведениях они руково­дствуются законами, кото­рые управляют природой. Выбирая симметричные формы, художник тем са­мым выражал свое понима­ние природной гармонии как устойчивости и равно­весия.

В городе Осло, столице Норвегии, есть выразитель­ный ансамбль природы и художественных произве­дений. Это Фрогнер – парк – комплекс садово-парко­вой скульптуры, который создавался в течение 40 лет.


Дом Пашкова Лувр (Париж)

© Сухачева Елена Владимировна, 2008-2009гг.

Симметричное рисование предметов правильной формы

Если на минутку задуматься и представить у себя в воображении какой-либо предмет, то в 99% случаев фигура, пришедшая на ум, будет правильной формы. Лишь 1 % людей, точнее их воображение, нарисует замысловатый объект, выглядящий совсем неправильно или непропорционально. Это скорее исключение из правил и относится к нетрадиционно размышляющим личностям с особым взглядом на вещи. Но возвращаясь к абсолютному большинству, стоит сказать, что существенная доля правильных предметов все же преобладает. В статье пойдет речь исключительно о них, а именно о симметричном рисовании таковых.

Изображение правильных предметов: всего несколько шагов до законченного рисунка

Прежде чем приступить к рисованию симметричного предмета, нужно его выбрать. В нашем варианте это будет ваза, но даже если она никак не напоминает то, что решили изображать вы, не отчаивайтесь: все шаги абсолютно идентичны. Придерживайтесь последовательности и все получится:

  1. У всех предметов правильной формы есть так называемая центральная ось, которую при симметричном рисовании обязательно стоит выделить. Для этого можно даже воспользоваться линейкой и провести по центру альбомного листа прямую линию.
  2. Далее внимательно посмотрите на выбранный вами предмет и постарайтесь перенести его пропорции на лист бумаги. Сделать это несложно, если с обеих сторон проведенной заранее линии, наметить легкие штрихи, которые впоследствии станут очертаниями рисуемого предмета. В случае с вазой необходимо выделить горлышко, донышко и самую широкую часть корпуса.
  3. Не забывайте о том, что симметричное рисование не терпит неточностей, поэтому если есть некоторые сомнения относительно намеченных штрихов, или вы не уверены в правильности собственного глазомера, перепроверьте отложенные расстояния при помощи линейки.
  4. Последний шаг — соединение всех линий воедино.

Симметричное рисование доступно компьютерным пользователям

В силу того что большинство окружающих нас предметов имеют правильные пропорции, иначе говоря симметричны, разработчики компьютерных приложений создали программы, в которых легко можно нарисовать абсолютно все. Достаточно лишь скачать их и наслаждаться творческим процессом. Однако помните, машина никогда не станет заменой остро наточенному карандашу и альбомному листу.

что такое симметрия? | Уроки по ИЗО

что такое симметрия?