Онлайн начертить треугольник – Произвольный треугольник по заданным параметрам

Содержание

Произвольный треугольник по заданным параметрам

Результат расчета параметров заданного треугольника

Представляем Вам калькулятор, который позволял рассчитывать все возможные параметры треугольника по заданным параметрам.

Хотелось бы обратить Ваше внимание именно на то, что это универсальный бот. Он рассчитывает все параметры произвольного треугольника, при произвольно заданных параметрах. Такого бота вы не найдете нигде.

Вам известна сторона и две высоты? или две стороны и медиана? Или биссектриса два угла и основание треугольника?

По любым запросам, мы можем получить правильный расчет параметров треугольника.

Вам нет необходимости искать формулы и делать расчет самостоятельно. За вас уже все сделано.

Создайте запрос и получите точный ответ.

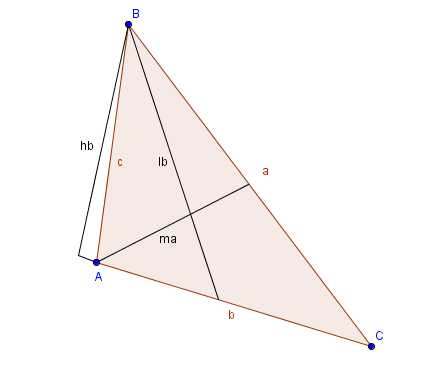
Показан произвольный треугольник. Сразу оговоримся как и что обозначается, дабы в дальнейшем не было путаницы и ошибок в расчетах.

Стороны противоположные любому углу называются так же только маленькой буквой. То есть напротив угла А лежит сторона треугольника а, стороне с противостоит угол С.

ma — это медина, падающая на сторону а, соответственно есть еще медианы mb и mc падающие на соответствующие стороны.

lb — это биссектриса , падающая на сторону b, соответственно есть еще биссектрисы la и lc падающие на соответствующие стороны.

hb — это высота, падающая на сторону b, соответственно есть еще высоты ha и hc падающие на соответствующие стороны.

Ну и второе, помните что треугольником является фигура в которой присутствует фундаментальное правило:

Сумма любых(!) двух сторон должна быть больше третьей.

Поэтому не удивляйтесь если получите ошибку При таких данных треугольника не существует при попытке рассчитатать параметры треугольника со сторонами 3, 3 и 7.

Синтаксис

Для позволяателей XMPP клиентов запрос вот такой treug <список параметров>

Для пользователй сайта, все сделано на этой странице.

Список параметров — параметры которые известны, разделенные точкой с запятой

параметр записываетя как параметр=значение

Например если известна сторона а с значением 10, то так и записываем a=10

Более того, значения могут быть не только в виде вещественного числа, но и например как результат какого то выражения

Например если нам нужно посчитать площадь треугольника с сторонами 1, 3, то вот в запросе пишем a=1;b=3;c=sqrt(5)+1

А вот и сам список парметров которые могут фигурировать в расчетах.

Сторона a

Сторона b

Сторона c

Полупериметр p

Угол А

Угол B

Угол C

Площадь треугольника S

Высота ha на сторону a

Высота hb на сторону b

Высота hc на сторону c

Медиана ma на сторону a

Медиана mb на сторону b

Медиана mc на сторону c

Координаты вершин (xa,ya) (xb,yb) (xc,yc)

Примеры

Рассчитать параметры треугольника если известны сторона = 8, угол прилежащей к этой стороне =70 градусов и высота, падающая на эту сторону =2

пишем treug a=8;C=70;ha=2

Параметры треугольника по заданным параметрам

Сторона a = 8

Сторона b = 2.1283555449519

Сторона c = 7.5420719851515

Полупериметр p = 8.8352137650517

Угол А = 2.1882518638666 в градусах 125.37759631119

Угол B = 2.873202966917 в градусах 164.62240368881

Угол C = 1.221730476396 в градусах 70

Площадь треугольника S = 8

Высота ha на сторону a = 2

Высота hb на сторону b = 7.5175409662872

Высота hc на сторону c = 2.1214329472723

Медиана ma на сторону a = 3.8348889915443

Медиана mb на сторону b = 7.7012304590352

Медиана mc на сторону c = 4.4770789813853

Вот и все, все параметры треугольника.

Вопрос, почему мы сторону назвали а, а не в или с? Это не влияет на решение. Главное выдержать условие о котором я уже сказал «Стороны противоположные любому углу называются так же, только маленькой буквой.» А далее нарисовать в уме треугольник, и применить к заданному вопросу.

Можно было бы взять вместо а в, но тогда прилежащий угол будет не С а А ну и высота будет hb. Результат если вы проверите, будет один и тот же.

Как рассчитать треугольник если известны координаты его вершин?

Например вот такими (xa,ya) =3,4 (xb,yb) =-6,14 (xc,yc)=-6,-3

пишем запрос treug xa=3;ya=4;xb=-6;yb=14;xc=-6;yc=-3

и получаем

Параметры треугольника по заданным параметрам

Сторона a = 17

Сторона b = 11.401754250991

Сторона c = 13.453624047073

Полупериметр p = 20.927689149032

Угол А = 1.4990243938603 в градусах 85.887771155351

Угол B = 0.73281510178655 в градусах 41.987212495819

Угол C = 0.90975315794426 в градусах 52.125016348905

Площадь треугольника S = 76.5

Высота ha на сторону a = 9

Высота hb на сторону b = 13.418987695398

Высота hc на сторону c = 11.372400437582

Медиана ma на сторону a = 9.1241437954466

Медиана mb на сторону b = 14.230249470757

Медиана mc на сторону c = 12.816005617976

Удачных расчетов!!

Разбиение многоугольника на треугольники >>

abakbot.ru

Произвольный треугольник по заданным параметрам

Результат расчета параметров заданного треугольника

По любым запросам, мы можем получить правильный расчет параметров треугольника.

Вам нет необходимости искать формулы и делать расчет самостоятельно. За вас уже все сделано.

Создайте запрос и получите точный ответ.

Ну и второе, помните что треугольником является фигура в которой присутствует фундаментальное правило:

Сумма любых(!) двух сторон должна быть больше третьей.

Синтаксис

Для позволяателей XMPP клиентов запрос вот такой treug <список параметров>

Для пользователй сайта, все сделано на этой странице.

Список параметров — параметры которые известны, разделенные точкой с запятой

параметр записываетя как параметр=значение

Например если известна сторона а с значением 10, то так и записываем a=10

Например если нам нужно посчитать площадь треугольника с сторонами 1, 3, то вот в запросе пишем a=1;b=3;c=sqrt(5)+1

А вот и сам список парметров которые могут фигурировать в расчетах.

Сторона a

Сторона b

Сторона c

Полупериметр p

Угол А

Угол B

Угол C

Площадь треугольника S

Высота ha на сторону a

Высота hb на сторону b

Высота hc на сторону c

Медиана ma на сторону a

Медиана mb на сторону b

Медиана mc на сторону c

Координаты вершин (xa,ya) (xb,yb) (xc,yc)

Примеры

пишем treug a=8;C=70;ha=2

Параметры треугольника по заданным параметрам

Сторона a = 8

Сторона b = 2.1283555449519

Сторона c = 7.5420719851515

Полупериметр p = 8.8352137650517

Угол А = 2.1882518638666 в градусах 125.37759631119

Угол B = 2.873202966917 в градусах 164.62240368881

Угол C = 1.221730476396 в градусах 70

Площадь треугольника S = 8

Высота ha на сторону a = 2

Высота hb на сторону b = 7.5175409662872

Высота hc на сторону c = 2.1214329472723

Медиана ma на сторону a = 3.8348889915443

Медиана mb на сторону b = 7.7012304590352

Медиана mc на сторону c = 4.4770789813853

Вот и все, все параметры треугольника.

Как рассчитать треугольник если известны координаты его вершин?

Например вот такими (xa,ya) =3,4 (xb,yb) =-6,14 (xc,yc)=-6,-3

пишем запрос treug xa=3;ya=4;xb=-6;yb=14;xc=-6;yc=-3

и получаем

Параметры треугольника по заданным параметрам

Сторона a = 17

Сторона b = 11.401754250991

Сторона c = 13.453624047073

Полупериметр p = 20.927689149032

Угол А = 1.4990243938603 в градусах 85.887771155351

Угол B = 0.73281510178655 в градусах 41.987212495819

Угол C = 0.90975315794426 в градусах 52.125016348905

Площадь треугольника S = 76.5

Высота ha на сторону a = 9

Высота hb на сторону b = 13.418987695398

Высота hc на сторону c = 11.372400437582

Медиана ma на сторону a = 9.1241437954466

Медиана mb на сторону b = 14.230249470757

Медиана mc на сторону c = 12.816005617976

Удачных расчетов!!

abakbot.ru

Стороны треугольника | Онлайн калькуляторы, расчеты и формулы на GELEOT.RU

Зная стороны треугольника, можно найти все остальные его параметры по выведенным для треугольника формулам, просто подставив их значения. Периметр треугольник будет представлять собой сумму всех его сторон, а площадь выводится по формуле Герона, как квадратный корень из произведения полупериметра на его разность с каждой стороной по очереди, и деленному на два. P=a+b+c S=√(p(p-a)(p-b)(p-c)/2)

Все углы в треугольнике, зная стороны, можно найти через теорему косинусов. (рис.75) cos⁡α=(b^2+c^2-a^2)/2bc

В произвольном треугольнике также есть три медианы m (делящие противоположную сторону пополам), три биссектрисы l (делящие угол пополам) и три высоты h (перпендикуляры из угла к стороне или ее проекции). Все их можно вычислить, имея в распоряжении значения трех сторон. Формула медианы, которая опущена на сторону c.(рис.75.1) m_c=√(2a^2+2b^2-c^2 )/2

Найти медиану, опущенную на сторону a или b, можно заменив необходимые стороны в формуле так, чтобы сторона, поделенная медианой пополам, была со знаком «–». m_a=√(2b^2+2c^2-a^2 )/2 m_b=√(2a^2+2c^2-b^2 )/2

Формула биссектрисы, которая выходит из угла γ и опущена на сторону с. (рис.75.2) l_c=√(ab(a+b+c)(a+b-c))/(a+b)

Чтобы найти биссектрисы, которые выходят из двух других углов, нужно преобразовать формулу аналогично формуле медианы, где противоположная сторона со знаком «–». l_b=√(ac(a+b+c)(a+c-b))/(a+c) l_a=√(bc(a+b+c)(b+c-a))/(b+c)

Формула высоты, которая опущена на сторону a, b или c видоизменяется таким образом, чтобы в знаменателе была нужная сторона.(рис.75.3) h_a=(2√(p(p-a)(p-b)(p-c) ))/a h_b=(2√(p(p-a)(p-b)(p-c) ))/b h_c=(2√(p(p-a)(p-b)(p-c) ))/c

Также в любом треугольнике можно провести среднюю линию, которая также как медиана обозначается буквой m, поэтому для их разделения, будем использовать заглавную M для средней линии. Средняя линия параллельна той стороне, которая выбрана основанием треугольника, и равна ее половине. Среди свойств средней линии можно отметить, что боковые стороны она делит на две равные части, поэтому если начертить все три средние линии в треугольнике, то получится еще один треугольник, подобный первому, в два раза меньше. (рис. 75.7) M_a=a/2 M_b=b/2 M_c=c/2

В каждый треугольник можно вписать окружность и описать ее вокруг него. Центр вписанной в треугольник окружности будет находиться на пересечении его биссектрис, а радиус будет опущен под прямым углом к любой стороне и его формула выводится также по Герону. (рис.75.5) r=√(((p-a)(p-b)(p-c))/p)

Центр описанной вокруг произвольного треугольника окружности находится на пересечении его медиатрисс (срединных перпендикуляров, радиус опущен в любую вершину или угол, и вычисляется по следующей формуле. (рис.75.6) R=abc/(4√(p(p-a)(p-b)(p-c)))

geleot.ru

Нахождение углов треугольника по заданным сторонам

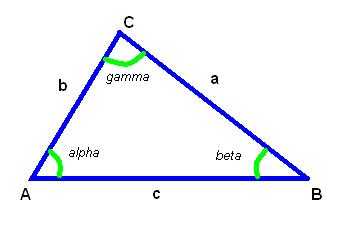
От нашего пользователя поступил запрос на создание калькулятора, рассчитывающего углы треугольника по заданным сторонам — Расчет углов треугольника.

Для треугольника, в отличие от, скажем, четырехугольника, эта задача имеет решение, ибо треугольник можно однозначно определить по трем сторонам (а также по двум сторонам и углу между ними, и по стороне и двум прилежащим углам).

Стороны в треугольнике, кстати сказать, должны следовать неравенству треугольника, то есть, сумма любых двух сторон должна быть больше третьей стороны.
Математически (см. рисунок) это выражается системой

В случае невыполнения хотя бы одного из условий треугольник называют вырожденным. Собственно, это и не треугольник уже.

Идем дальше — при известных сторонах углы проще всего определить, пользуясь теоремой косинусов, частным случаем которой является теорема Пифагора (см. рисунок)

, откуда

Калькулятор ниже рассчитывает углы по введенным длинам сторон. Если треугольник вырожденный, то в результате будут нули.

Нахождение углов треугольника по заданным сторонам

Точность вычисления

Знаков после запятой: 2

Угол alpha (градусы)

Угол beta (градусы)

Угол gamma (градусы)

save Сохранить share Поделиться extension Виджет

planetcalc.ru

Площадь треугольника. Онлайн-калькулятор

Онлайн-калькулятор для расчета площади треугольника поможет Вам найти площадь треугольника несколькими способами в зависимости от известных данных. Наш калькулятор не просто рассчитает площадь треугольника, но и покажет подробное решение, которое будет показано под калькулятором. Поэтому данный калькулятор удобно использовать не только для быстрых расчетов, но и для проверки своих вычислений. С помощью данного калькулятора вы сможете найти площадь треугольника по следующим формулам: через основание и высоту, через две стороны и угол, по трем сторонам (формула Герона), через радиус вписанной окружности, через радиус описанной окружности.

Выберите способ расчета площади:

через основание и высотучерез две стороны и уголпо трем сторонам (формула Герона)через радиус вписанной окружностичерез радиус описанной окружности

Рассчитать

Треугольник – это геометрическая фигура, которая образована тремя отрезками. Эти отрезки называются сторонами треугольниками, а точки соединения отрезков – вершинами треугольника. В зависимости от соотношения сторон треугольники бывают нескольких видов: равнобедренный треугольник (две стороный треугольника равны между собой, эти стороны называются боковыми сторонами, а третья сторона называется основанием треугольника), равносторонний треугольник (у треугольника все три стороны равны), прямоугольный треугольник (один угол треугольника прямой).

Как найти площадь треугольника?

Найти площадь треугольника очень просто, достаточно воспользоваться нашим калькулятором или рассчитать самостоятельно, воспользовавшись формулой площади треугольника. В зависимости от того, какие данные известны, для расчета площади треугольника использует несколько способов:

1) через основание и высоту

a – основание треугольника,
h – высота треугольника.

2) через две стороны и угол

a, b – стороны треугольника,
α – угол между сторонами.

3) По трем сторонам. Формула Герона.

a, b, с – стороны треугольника,
p – полупериметр треугольника.

4) Через радиус вписанной окружности.

a, b, с – стороны треугольника,
p – полупериметр треугольника,
r – радиус вписанной окружности.

5) Через радиус описанной окружности.

a, b, с – стороны треугольника,
R – радиус описанной окружности.

Вы всегда сможете проверить правильность расчета площади треугольника с помощью нашего калькулятора.

calc.by

Построение, создание треугольника Паскаля онлайн

Треугольник Паскаля — элегантный математический треугольник, представляющий собой бесконечную таблицу биноминальных коэффициентов. Таблица иллюстрирует скрытые соотношения между числами, которые естественным образом возникают в теории чисел, комбинаторике, теории вероятностей и алгебре.

Суть треугольной последовательности

Число 1 — важное число, а 11? Любопытно, что 11 × 11 = 121, 11 × 11 × 11 = 1331, а 11 × 11 × 11 × 11 = 14641. Если выстроить эти числа сверху вниз и представить их в виде отдельных цифр, то получится интересная формация:

1
1 1
1 2 1
1 3 3 1
1 4 6 4 1

Эти цифры — первые строки знаменитого треугольника Паскаля. Далее таблица строится по следующему принципу: по краям записываются единицы, а внутри ряда числа формируются путем суммы цифр, расположенных рядом выше слева и справа от искомых. Данная таблица знаменита в математике своей элегантностью, симметрией и неожиданными связями между числами. Связи таблицы с другими математическими сферами превратили треугольник Паскаля в Священный Грааль математики.

История открытия

Считается, что таблица была открыта Блезом Паскалем в 1653 году, однако происхождение формации гораздо древнее. Первое упоминание о бесконечной треугольной таблице встречается в трудах индийских математиков 10-го века, а наиболее полная информация о треугольнике представлена в работе китайского математика Шицзе, опубликованной в 1303 году. Однако и Шизце лишь упомянул о формации, создателем же треугольника Паскаля считается китайский ученый Ян Хуэй, поэтому в Китае таблица биноминальных коэффициентов носит название «треугольник Хуэя».

Удивительные свойства

Симметрия — очевидное свойство треугольника Паскаля. Если из верхней единицы провести вертикальную прямую, то числа справа и слева будут симметричны. Диагонали треугольника также симметричны. Диагонали вообще обладают рядом уникальных свойств. Если первая диагональ, как восточная, так и западная, представляет собой ряд сплошных единиц, то вторая — ряд натуральных чисел, третья — ряд треугольных чисел, а четвертая — тетраэдрических.

Треугольные числа (1, 3, 6, 10…) — это числа, при помощи которых строятся плоские треугольники. Простыми словами, если в двухмерной игре вы захотите составить треугольник из круглых элементов, то вам понадобится выстроить элементы в количестве, советующему треугольным числам: сначала 6 кругов, потом 3, потом 1.
Тетраэдрические числа (1, 4, 10, 20…) используются для построения объемных тетраэдров. Проще говоря, если вам понадобится сложить пушечные ядра аккуратной пирамидой, то в основании вам потребуется уложить 20 ядер, на них еще 10, сверху 4 и увенчать пирамиду одним верхним ядром.

Кроме того, если в треугольнике Паскаля четные числа заменить единицами, а нечетные — нулями, то получится треугольник Серпинского — известный фрактал, построенный польским математиком в начале 20 века.

Треугольник Паскаля также имеет удивительную связь с алгеброй. Если мы разложим бином Ньютона вида (1 + x)², то получим 1 + 2x + x². Если же это будет (1 + x)³, то в результате мы получим 1 + 3x + 3x² + x³. Если присмотреться, то биноминальные коэффициенты — это ни что иное как числа из соответствующего ряда треугольника Паскаля.

Построение треугольника Паскаля

Треугольник Паскаля — это бесконечная таблица элементов. При помощи нашего калькулятора вы можете построить таблицу любой размерности, однако не рекомендуется использовать слишком большие числа (n>100), так как столь огромные таблицы не имеют практического применения, а онлайн-калькулятор строит их слишком долго. Помимо элегантных свойств, используемых для решения биноминальных уравнений или построения тетраэдрических последовательностей, таблица Паскаля находит применение в комбинаторике.

Примеры из реальной жизни

Подсчет количества способов

Если на кафедре работают 7 математиков, и троих из них нужно отправить на городскую олимпиаду, то сколькими способами можно это сделать? Это стандартная задача на комбинаторику, в котором важен порядок элементов, то есть вариант «Сидоров, Иванов и Петров» отличается от варианта «Иванов, Петров, Сидоров», хотя выбранная группа математиков одна и та же. Такая ситуация возникает в случае, если преподаватели должны участвовать в разных конкурсах. При «ручном» решении нам пришлось бы использовать стандартные формулы для комбинаторики, однако проще воспользоваться свойствами треугольника Паскаля.

Для ответа на вопрос нам достаточно построить треугольник с n = 10, найти седьмой ряд и третье число в нем. Таким образом, существует 35 способов объединить математиков для поездки на олимпиаду.

Определение вероятности

В корзине лежит 20 шаров, пронумерованных от 1 до 20. Наугад мы берем 3 шара. Какова вероятность, что мы вытащим шары с номерами 5, 12 и 13? Для решения этой задачи нам потребуется построить треугольник Паскаля с n = 20, после чего найти двадцатый ряд и третье число в нем. Вытащить три шара можно 1140 способами. Вероятность наступления нашего события составит 3 из 1140.

Заключение

Треугольник Паскаля — простая таблица, которая таит в себе огромное количество математических тайн. Члены рядов связаны с биноминальными коэффициентами, совершенными числами, числами Фибоначчи, тетраэдрическими и треугольными числами. Используйте наш калькулятор для построения сетки необходимой вам размерности для решения самых разных математических задач.

bbf.ru

Сделать чертеж онлайн

У многих пользователей может возникнуть необходимость чертить онлайн. Это может какой-либо эскиз, схема, план или техническая иллюстрация, которые необходимо создать на ПК с помощью соответствующего инструментария. При этом на компьютере может не оказаться необходимых для этого программ, что побудит пользователя искать в сети онлайн ресурсы, способных помочь в создании нужного пользователю проекта. В данном материале я расскажу, как сделать чертёж онлайн, и какие сервисы нам в этом помогут.

Изучаем онлайн-ресурсы для выполнения чертежа онлайн

Содержание статьи:

Лучшие онлайн сервисы для черчения

Перейдём к непосредственному описанию сетевых сервисов онлайн. Замечу, что указанные сервисы для создания чертежей обладают довольно сжатым по сравнению с профессиональными программами функционалом, чего, впрочем, может быть достаточно для решения множества базовых задач.

Онлайн-редактор GLIFFY

Данный визуальный редактор GLIFFY обладает довольно широким инструментарием для создания чертежей и схематических изображений, включая множество шаблонов и схем для архитектурных проектов, блок-схем, сетевых диаграмм и других соответствующих целей.

Для работы с данным редактором перейдите на сайт cameralabs.org, при необходимости авторизуйтесь (доступна также авторизация через социальную сеть). После этого вам станет доступен экран редактирования, где вы сможете создать ваш чертёж.

Рабочий экран редактора «GLIFFY»

Слева расположены вкладки различных шаблонов (вы можете раскрыть вкладку, кликнув на ней), сверху – панель инструментов, а справа будет размещаться непосредственное поле для создания чертежа.

Вкладки с шаблонами фигур слева, которые можно раскрыть кликнув по ним

Для сохранения вашей работы нужно будет нажать вверху на «File» — «Сохранить» (или «Экспорт»).

Сервис draw.io

Англоязычный сервис draw.io поможет создать чертёж в режиме онлайн, начертав различные графики, схемы и диаграммы.

Для работы с данным сервисом перейдите на сайт draw.io. Ресурс спросит, куда сохранять созданные вами работы (выберите «Device» для сохранения на жёсткий диск).

Нажмите на «Create New Diagram» (создание новой диаграммы), выберите её имя, а также соответствующий шаблон для создания слева.

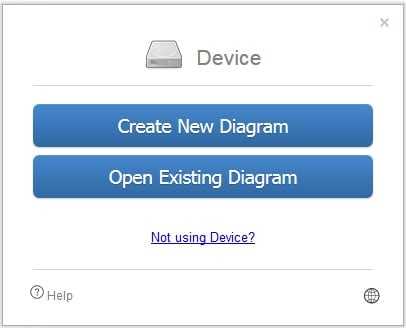Нажмите на «Create New Diagram» для создания нового чертежа

Выберите пустую начальную диаграмму (Blanc Diagramm) или какой-либо из уже имеющихся шаблонов диаграмм (charts), инженерных схем (Engineering), блок-схем (Flowcharts), разметки (layout), карт (maps) и других видов шаблонов

После того, как вы выбрали шаблон, нажмите на «Create» (Создать).

Далее вы перейдёте в экран редактирования. Слева представлены различные шаблоны черчения, сверху панель вспомогательных инструментов, справа – различные настройки отображения документов.

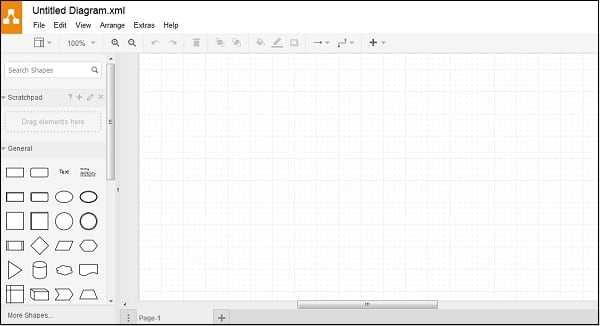Левая и центральная часть экрана редактирования сервиса «draw.io»

Для сохранения созданного чертежа нажмите на «File» — «Save as».

Сервис drawisland.com

Сервис drawisland.com – простой англоязычный сервис для черчения в Интернете. После перехода на него вас ждёт экран для создания чертежа с довольно ограниченным набором инструментов. Слева расположена панель инструментов, сверху вы можете выбрать размеры рисунка и повернуть его на 90 или 180 градусов, а справа доступ выбор диаметр инструмента для рисования, а также переключаться между слоями.

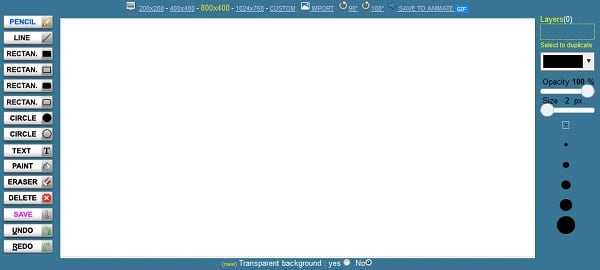Рабочее окно «drawisland.com»

Для сохранения созданного вами рисунка на диск нажмите на кнопку «Save» слева.

Сервис knin.com.ua

Данный сервис предназначен для создания технического плана строительного объекта, который можно будет позже сохранить к себе на ПК. Как и большинство аналогичных сервисов, данный сервис обладает набором встроенных графических шаблонов, делающих процесс создания технического плана помещения практичным и удобным, позволяя легко нарисовать чертёж онлайн.

Для начала работы с данным сервисом перейдите на сайт knin.com.ua.
Укажите справа сверху размеры помещения, а затем нажмите на кнопку «Создать».
Если будет необходимо добавить ещё помещение, тогда вновь укажите его размеры и нажмите на «Создать».
После того, как все нужные помещения будут созданы, нажмите на «Продолжить».
После этого вам справа станут доступны различные графические объекты – окна, стены, предметы интерьера и так далее, которые вы сможете помещать на ваш объект.
Далее, как план объекта будет создан, вы сможете сохранить его на диск, нажав на кнопку «Сохранить» внизу.

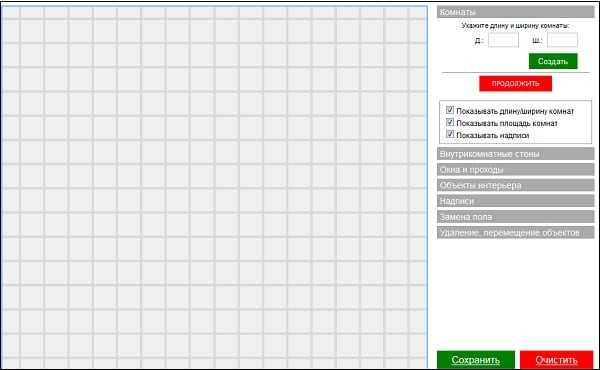Рабочее окно сервиса «knin.com.ua»

Сервис sketch.io

«Sketch.io» — ещё один простой англоязычный ресурс для построения простых чертежей, создания графических набросков и зарисовок. Функционал сервиса довольно прост, и подойдёт, в первую очередь новичкам в деле создания чертежей.

Для работы с сервисом перейдите на сайт sketch.io.
Справа размещена панель инструментов, с помощью которой можно выполнять все необходимые операции.
После того, как рисунок будет создан, нажмите на кнопку «Export» (дискетка сверху), затем на «Save» — «Download».

Панель инструментов сервиса sketch.io

Программы для черчения

Также при описании онлайн сервисов для создания эскиза проекта, нельзя обойти стороной и ряд популярных программ, созданных специально для таких целей. При этом большинство из них обладает платным характером, так как для решения профессиональных задач функционала бесплатных программ может быть недостаточно.

«Autodesk AutoCAD» — одна из наиболее известных систем автоматизированного проектирования (САПР), предназначенных для создания различных видов чертежей, схем, графиков. Позволяет создавать 2Д и 3Д чертежи на высокопрофессиональном уровне, обладает богатым функционалом, отлично справляется с рендерингом 3Д-объектов, умеет работать с 3Д-принтером. Поддерживается работа с чертежами в формате DVG, DWF, DXF;
«Аскон Компас» — это целый комплекс программных решений для осуществления черчения и диаграмм, довольно популярных на территории РФ. Данные решения поддерживают множество форматов электронных чертежей, обладают большой базой присоединяемых библиотек, при этом довольно просты и удобны в работе;
«nanoCAD» — бесплатная программа для начинающих, включающая необходимый набор базовых инструментов для осуществления проектирования и создания чертежей. Программа направления на создание преимущественно 2Д-чертежей, поддерживает работу с DWG и DXF чертежами, достоинством программы является быстрый вывод объектов, работы с DirectX и так далее.

Заключение

В данном материале мной были рассмотрены несколько популярных сервисов, позволяющих реализовать черчение онлайн. Все они обладают довольно разным функционалом, в целом уступая своим профессиональным стационарным конкурентам (к примеру, «Autodesk AutoCAD»). Если же вы только пробуете свои силы в черчении, то рекомендую воспользоваться как перечисленными мной онлайн-сервисами, так и упомянутой бесплатной программой «nanoCAD» — описанные инструменты прекрасно подойдут для получения базовых навыков при создании нужных вам чертежей.

it-doc.info