словообразование — Треугольник, но угла трИ?
При образовании сложных слов на основе числительных в большинстве случаев используется сложение ЧИСЛИТЕЛЬНОГО В ФОРМЕ Р.П. с основой опорного существительного или прилагательного (исключение: числительные сто, девяносто используются в форме И.п.) Способ образования прилагательных: суффиксальное сложение. Два года → двух-лет-н-ий и дву-лет-н-ий (усеченная форма). Три палубы → трех- палуб-н-ый, три угла → тре-уголь- н –ый (усеченная форма)→ треугольн-ик.
ИНФОРМАЦИЯ ПО ПОВОДУ УСЕЧЕННЫХ ФОРМ (кстати, интересный и неоднозначный вопрос для обсуждения):
Форма ДВУ является формой существовавшего когда-то двойственного числа. Можно сказать, что число два в этом случае имеет обобщенное значение и задает определенное качество сложному слову (становится возможной замена синонимом): двужильный человек (сильный), двуличный человек (лицемерный.
Сложные слова с числительным три образуются с помощью основной количественной формы Р.
Так каков же Ваш вариант образования слова треугольник: роль буквы Е, способ образования? Если форму ТРЕ нельзя назвать усеченной формой ТРЕХ, то что это за форма?
ИНФОРМАЦИЯ ИЗ ИНТЕРНЕТА
Из истории слов Число «3» входит в сложные слова в разных формах. Во-первых, существует ряд слов, образованных сложением с основой тре- (от не сохранившегося наречия тре – «трижды»): треугольник, трезубец, треножник, треух, трезвон, треволнение.
Во-вторых, сращением со словом три образованы числительные тринадцать, тридцать, триста, а также некоторые другие слова: Тригорское (от «три горы»), тридесятое (царство), втридорога.
Обе эти модели непродуктивны. Зато продуктивна модель с основой трех – формой родительного падежа числительного три (трехдневный, трехсложный, трехведерный).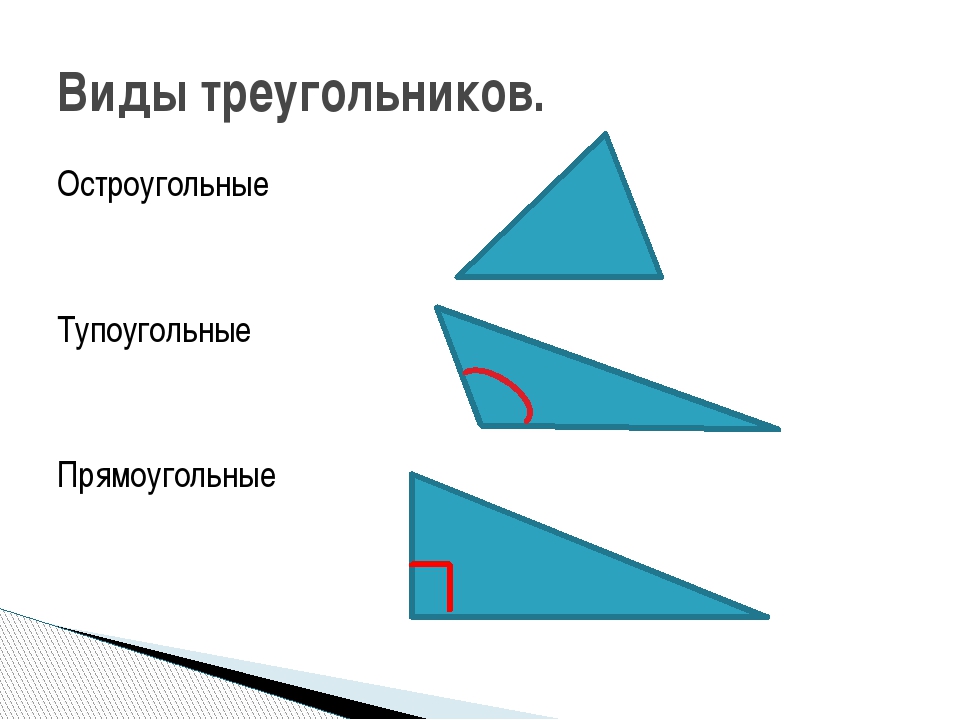
Сложные слова с количественным числительным два также образуются от разных основ: дву- и двух-: двуглавый и двухголовый, двуличный и двухместный. Основа дву- – это тоже форма родительного падежа, но только для парных предметов (т.е. предметов, нормально существующих в паре).
треугольные символы — ▲
▩ квадратные символы | ╬ линейные символы |Нажмите на значок, чтобы скопировать в буфер обмена ▼
⊿▲△▴▵▶▷▸▹►▻▼▽▾▿◀◁◂◃◄◅◢◣◤◥◬◭◮◸◹◺◿∇∆
※ Все символы являются символами Юникода, а не изображением или комбинированными символами. Но вы также можете комбинировать их самостоятельно. ※
| символ текста | смысл | Копировать / Вставить |
|---|---|---|
| ▲ | черный треугольник | Копировать |
| △ | белый треугольник | Копировать |
| ▴ | черный треугольник, направленный вверх | Копировать |
| ▵ | белый треугольник, направленный вверх | Копировать |
| ▶ | черный правый треугольник | Копировать |
| ▷ | белый правый треугольник | Копировать |
| ▸ | черный правый маленький треугольник | Копировать |
| ▹ | белый правый маленький треугольник | Копировать |
| ► | черный указатель вправо | Копировать |
| ▻ | белый указатель вправо | Копировать |
| ▼ | черный треугольник, направленный вниз | Копировать |
| ▽ | белый треугольник, направленный вниз | Копировать |
| ▾ | Копировать | |
| ▿ | белый треугольник, направленный вниз | Копировать |
| ◀ | черный треугольник влево | Копировать |
| ◁ | белый треугольник влево | Копировать |
| ◂ | черный треугольник влево | Копировать |
| ◃ | белый левый маленький треугольник | Копировать |
| ◄ | черный указатель влево | Копировать |
| ◅ | белый указатель влево | Копировать |
| ◢ | черный нижний прямоугольный треугольник | Копировать |
| ◣ | черный нижний левый треугольник | Копировать |
| ◤ | черный верхний левый треугольник | Копировать |
| ◥ | черный верхний правый треугольник | Копировать |
| ◬ | белый треугольник с точкой | Копировать |
| ◭ | направленный вверх треугольник с левой половиной черного цвета | Копировать |
| ◮ | направленный вверх треугольник с правой половиной черного цвета | Копировать |
| ◸ | верхний левый треугольник | Копировать |
| ◹ | верхний правый треугольник | Копировать |
| ◺ | нижний левый треугольник | Копировать |
| ◿ | нижний правый треугольник | Копировать |
Как правильно пишется: треугольник или триугольник? — 4 info
Как правильно пишется: треугольник или триугольник?
Данное слово пишется исключительно через гласную «е», то есть — «треугольник». Написание «триугольник» — будет считаться ошибочным, но так пишут, думая, что корнем является «три», отсюда и такое написание. Но нет, корень в слове «три» — «тр». Это слово образовалось от двух слов «три» и «угол» и соответственно имеет два корня. А со школьной программы нам известно, что эти корни соединяются с помощью гласных «е» и «о». В данном случае это гласная «е»: трЕугольник.
Написание «триугольник» — будет считаться ошибочным, но так пишут, думая, что корнем является «три», отсюда и такое написание. Но нет, корень в слове «три» — «тр». Это слово образовалось от двух слов «три» и «угол» и соответственно имеет два корня. А со школьной программы нам известно, что эти корни соединяются с помощью гласных «е» и «о». В данном случае это гласная «е»: трЕугольник.
Это слово, включает в себя два корня: «три» и «угол». Между двумя корнями сложного слова могут служить только две гласные: «о» и «е». Поэтому от 1-го корня остатся «тр», а место буквы «и» соединительная гласная «е». Поэтому и пишется трЕугольник.
Правильно писать треугольник, это можно проверить в словаре.
Заданное сложное имя существительное составлено из корней двух слов: числительного три и прилагательного угольный.
Ко второй части этого слова, как видно, никаких вопросов нет, только к первой части.
Но и с ней разобраться не представляет особых трудностей.
Давайте более внимательно посмотрим на слово три, давайте подберем к нему однокоренные (родственные) слова.
Вот некоторые из них: тр/ое, тр/ойка, тр/оечка, тр/оечница, тр/етий, тр/еть, тр/етичный, в/тр/оем, у/тр/аивать.
Думаю, этих слов вполне достаточно, чтобы сделать вывод о том, что значимая часть, то есть корень — тр-.
А уж он при образовании сложного слова присоединяется ко второй части его посредством соединительной гласной е.
Соединительной гласной и не бывает.
Правильно пишется «Треугольник» простейший многоугольник, имеющий 3 вершины (угла) и 3 стороны; часть плоскости, ограниченная тремя точками и тремя отрезками, попарно соединяющими эти точки.
Слово треугольник образовано от сложного прилагательного «треугольный», а оно в свою очередь от двух слов «три» «угла» с помощью суффикса:
три угла — треугольный — треугольник.
У числительного «три» корнем является часть тр-, которая прослеживается в родственных словах:
трое, тройка, тройня, утроить, тршка.
Корни тр- и -уголь- объединяет в новое слово соединительная гласная е, как и в словах:
птицефабрика, овощехранилище, грязелечебница, мореплаватель.
Поэтому выберем вариант написания треугольник.
Написание соединительной морфемы е заметим в аналогичных сложных словах с первым корнем тр-:
треугольный, треуголка, треуголочка, трезубец, тренога.
Только в единственном слове трилистник пишется интерфикс и.
Треугольник: вершины, стороны, углы. Высота, биссектриса и медиана
Треугольник — это замкнутая ломаная линия, состоящая из трёх звеньев:
Вершины ломаной называются вершинами треугольника, а её звенья — сторонами треугольника. Углы, образованные двумя сторона треугольника, называются углами треугольника:
Углы, образованные двумя сторона треугольника, называются углами треугольника:
В треугольнике ABC вершины A, B и
Треугольник обычно обозначается тремя буквами, стоящими при его вершинах. Например, треугольник ABC, или BCA, или CBA. Вместо слова треугольник часто используется знак . Так, запись ABC будет читаться: треугольник ABC
.
У каждого треугольника 3 вершины, 3 стороны и 3 угла.
Высота
Высота треугольника — это перпендикуляр, опущенный из вершины треугольника на его основание. Высота треугольника может быть опущена и на продолжение основания.
Отрезок BN — это высота ABC. Отрезок EL высота DEF, опущенная на продолжение стороны DF.
Длина высоты — это длина отрезка от вершины угла до пересечения с основанием.
Каждый треугольник имеет три высоты.
Биссектриса
Биссектриса угла треугольника — прямая, делящая угол треугольника пополам. Длина отрезка этой прямой от вершины угла до точки пересечения с противоположной стороной называется длиной биссектрисы
Отрезок BN — это биссектриса ABC.
Каждый треугольник имеет три биссектрисы.
Медиана
Медиана треугольника — это отрезок, соединяющий вершину треугольника с серединой противоположной стороны. Длина этого отрезка называется длиной медианы.
Отрезок BN — это медиана ABC.
Каждый треугольник имеет три медианы.
Треугольник. Формулы и свойства треугольников.
Определение. Треугольник — фигура, которая состоит из трёх точек, не лежащих на одной прямой, и трёх отрезков, попарно соединяющих эти точки. Точки называются вершинами треугольника, а отрезки — его сторонами.
Типы треугольников
По величине углов
- Остроугольный треугольник — все углы треугольника острые.
- Тупоугольный треугольник — один из углов треугольника тупой (больше 90°).
- Прямоугольный треугольник — один из углов треугольника прямой (равен 90°).
По числу равных сторон
- Разносторонний треугольник — все три стороны не равны.
- Равнобедренный треугольник — две стороны равны.
- Равносторонним треугольник или правильный треугольник — все три стороны равны.
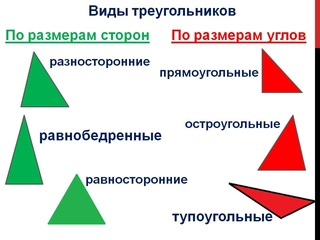
Вершины углы и стороны треугольника
Свойства углов и сторон треугольника
Сумма углов треугольника равна 180°:
α + β + γ = 180°
В треугольнике против большей стороны лежит больший угол, и обратно. Против равных сторон лежат равные углы:
если α > β, тогда a > b
если α = β, тогда a = b
Сумма длин двух любых сторон треугольника больше длины оставшейся стороны:
a + b > c
b + c > a
c + a > b
Теорема синусов
Стороны треугольника пропорциональны синусам противолежащих углов.
| a | = | b | = | c | = 2R |
| sin α | sin β | sin γ |
Теорема косинусов
Квадрат любой стороны треугольника равен сумме квадратов двух других сторон треугольника минус удвоенное произведение этих сторон на косинус угла между ними.
a2 = b2 + c2 — 2bc·cos α
b2 = a2 + c2 — 2ac·cos β
c2 = a2 + b2 — 2ab·cos γ
Теорема о проекциях
Для остроугольного треугольника:
a = b cos γ + c cos β
b = a cos γ + c cos α
c = a cos β + b cos α
Формулы для вычисления длин сторон треугольника
Формулы сторон через медианыa = 23√2(mb2 + mc2) — ma2
b = 23√2(ma2 + mc2) — mb2
c = 23√2(ma2 + mb2) — mc2
Медианы треугольника
Определение. Медиана треугольника ― отрезок внутри треугольника, который соединяет вершину треугольника с серединой противоположной стороны.
Свойства медиан треугольника:
Медианы треугольника пересекаются в одной точке.
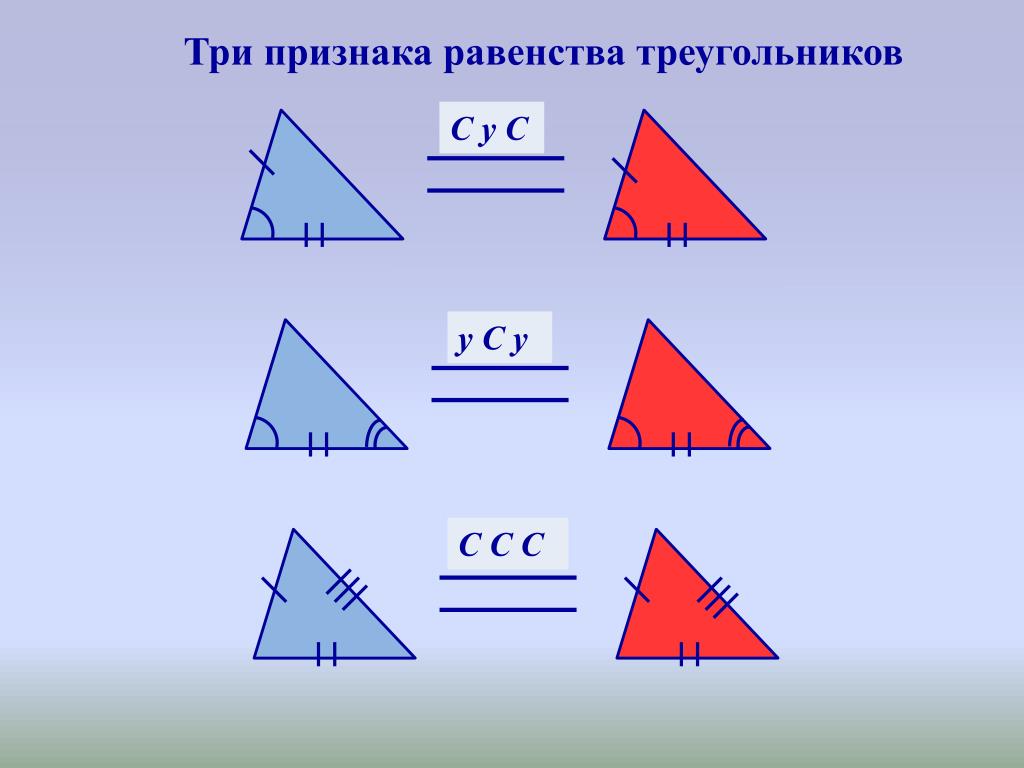 (Точка пересечения медиан называется центроидом)
(Точка пересечения медиан называется центроидом)В точке пересечения медианы треугольника делятся в отношении два к одному (2:1)
AOOD = BOOE = COOF = 21
Медиана треугольника делит треугольник на две равновеликие части
S∆ABD = S∆ACD
S∆BEA = S∆BEC
S∆CBF = S∆CAF
Треугольник делится тремя медианами на шесть равновеликих треугольников.
S∆AOF = S∆AOE = S∆BOF = S∆BOD = S∆COD = S∆COE
Из векторов, образующих медианы, можно составить треугольник.
Формулы медиан треугольника
Формулы медиан треугольника через стороны
ma = 12√2b2+2c2-a2
mb = 12√2a2+2c2-b2
mc = 12√2a2+2b2-c2
Биссектрисы треугольника
Определение.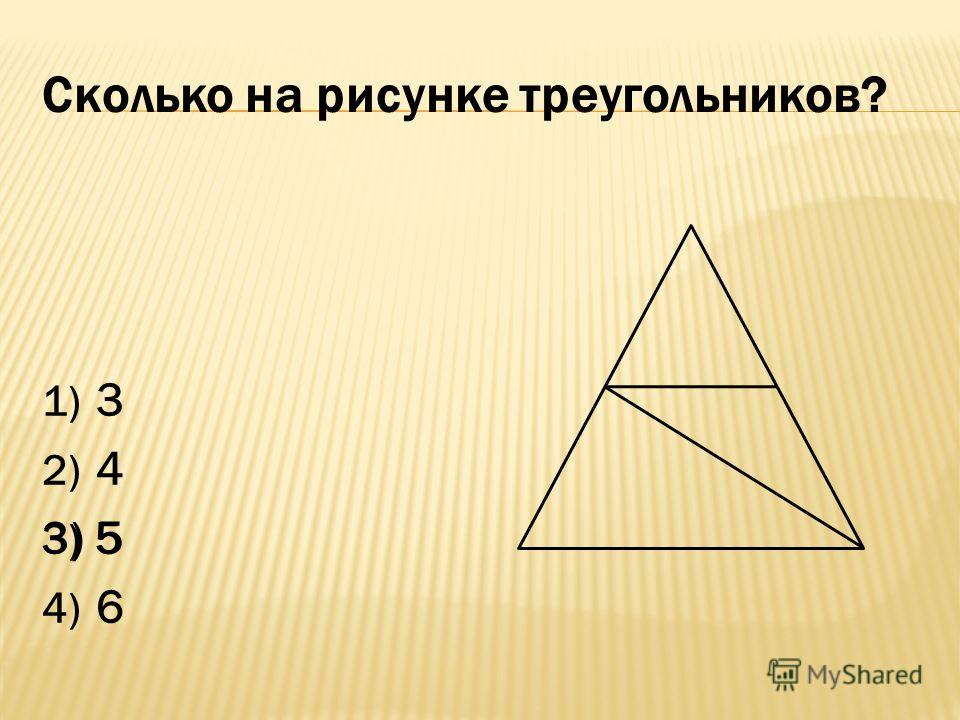 Биссектриса угла — луч с началом в вершине угла, делящий угол на два равных угла.
Биссектриса угла — луч с началом в вершине угла, делящий угол на два равных угла.
Свойства биссектрис треугольника:
Биссектрисы треугольника пересекаются в одной точке, равноудаленной от трех сторон треугольника, — центре вписанной окружности.
Биссектриса треугольника делит противолежащую сторону на отрезки, пропорциональные прилежащим сторонам треугольника
AEAB = ECBC
Угол между биссектрисами внутреннего и внешнего углов треугольника при одной вершине равен 90°.
Угол между lc и lc‘ = 90°
Если в треугольнике две биссектрисы равны, то треугольник — равнобедренный.
Формулы биссектрис треугольника
Формулы биссектрис треугольника через стороны:
la = 2√bcp(p — a)b + c
lb = 2√acp(p — b)a + c
lc = 2√abp(p — c)a + b
где p = a + b + c2 — полупериметр треугольника
Формулы биссектрис треугольника через две стороны и угол:
la = 2bc cos α2b + c
lb = 2ac cos β2a + c
lc = 2ab cos γ2a + b
Высоты треугольника
Определение. Высотой треугольника называется перпендикуляр, опущенный из вершины треугольника на прямую содержащую противоположную сторону.
Высотой треугольника называется перпендикуляр, опущенный из вершины треугольника на прямую содержащую противоположную сторону.
- внутри треугольника — для остроугольного треугольника;
- совпадать с его стороной — для катета прямоугольного треугольника;
- проходить вне треугольника — для острых углов тупоугольного треугольника.
Свойства высот треугольника
Высоты треугольника пересекаются в одной точке, называемой ортоцентром треугольника.
Если в треугольнике две высоты равны, то треугольник — равнобедренный.
ha:hb:hc = 1a:1b:1c = (bc):(ac):(ab)
Формулы высот треугольника
Формулы высот треугольника через сторону и угол:ha = b sin γ = c sin β
hb = c sin α = a sin γ
hc = a sin β = b sin α
Формулы высот треугольника через сторону и площадь:ha = 2Sa
hb = 2Sb
hc = 2Sc
Формулы высот треугольника через две стороны и радиус описанной окружности:ha = bc2R
hb = ac2R
hc = ab2R
Окружность вписанная в треугольник
Определение.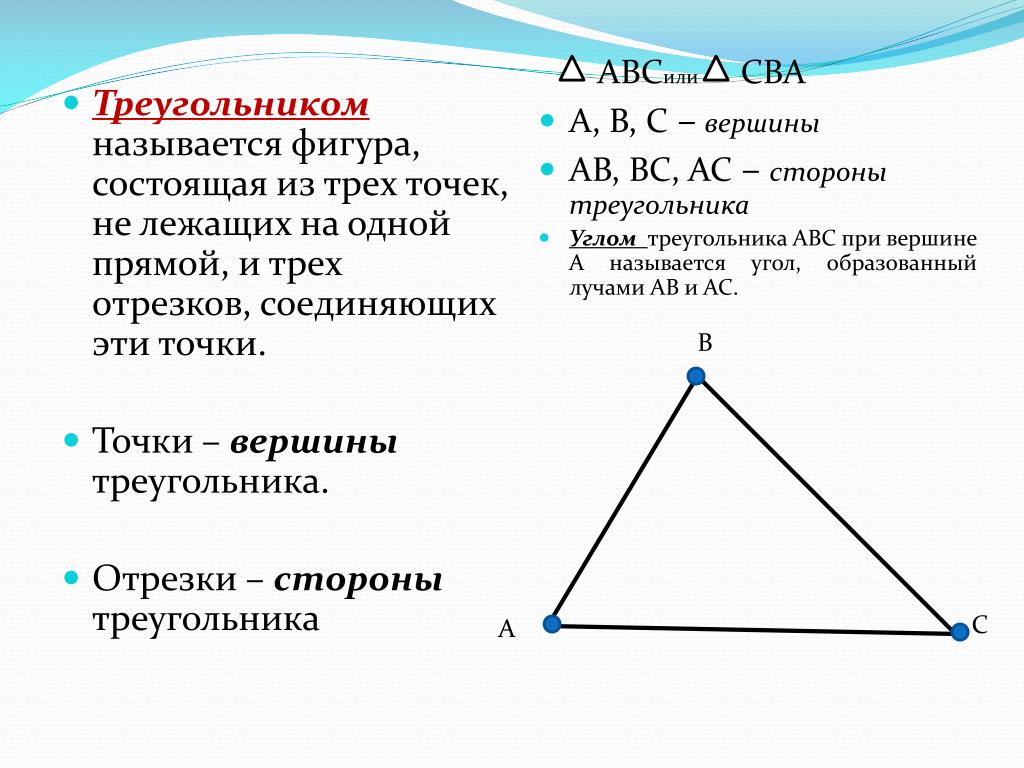 Окружность называется вписанной в треугольник, если она касается всех трех его сторон.
Окружность называется вписанной в треугольник, если она касается всех трех его сторон.
Свойства окружности вписанной в треугольник
Центр вписанной в треугольник окружности лежит на пересечении биссектрис внутренних углов треугольника.
В любой треугольник можно вписать окружность, и только одну.
Формулы радиуса окружности вписанной в треугольник
Радиус вписанной в треугольник окружности равен отношению площади треугольника к его полупериметру: Радиус вписанной в треугольник окружности через три стороны:r = (a + b — c)(b + c — a)(c + a — b)4(a + b + c)
Радиус вписанной в треугольник окружности через три высоты:Окружность описанная вокруг треугольника
Определение. Окружность называется описанной вокруг треугольника, если она содержит все вершины треугльника.
Свойства окружности описанной вокруг треугольника
Центр описанной вокруг треугольника окружности лежит на пересечении серединных перпендикуляров к его сторонам.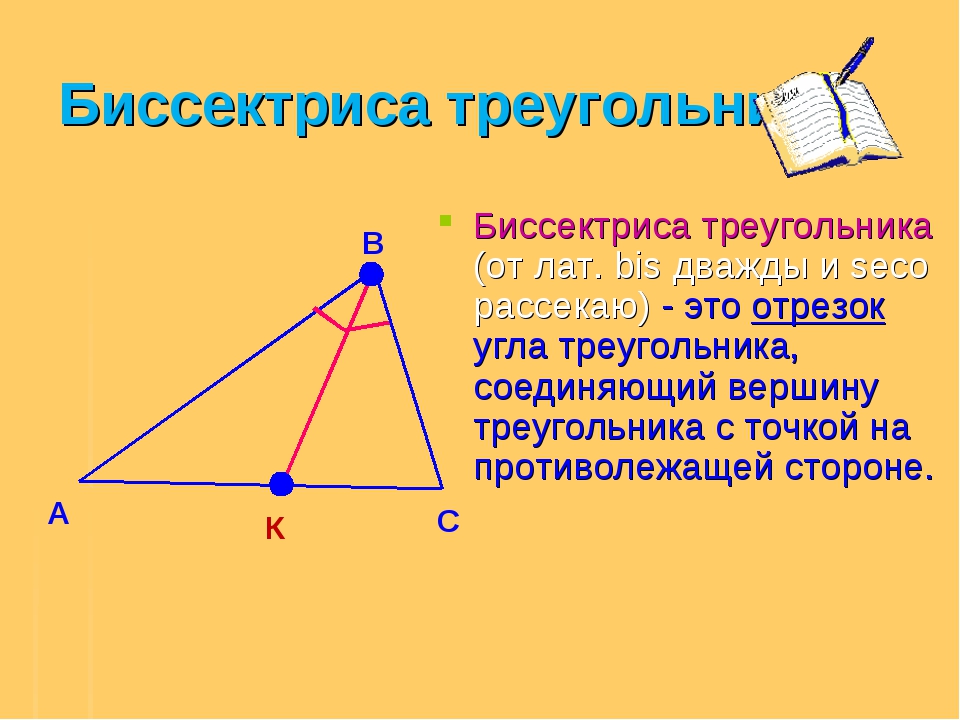
Вокруг любого треугольника можно описать окружность, и только одну.
Свойства углов
Центр описанной окружности лежит внутри остроугольного треугольника, снаружи тупоугольнго треугольника, на середине гипотенузы прямоугольного треугольника.
Формулы радиуса окружности описанной вокруг треугольника
Радиус описанной окружности через три стороны и площадь: Радиус описанной окружности через площадь и три угла:R = S2 sin α sin β sin γ
Радиус описанной окружности через сторону и противоположный угол (теорема синусов):R = a2 sin α = b2 sin β = c2 sin γ
Связь между вписанной и описанной окружностями треугольника
Если d — расстояние между центрами вписанной и описанной окружностей, то.rR = 4 sinα2sinβ2sinγ2 = cos α + cos β + cos γ — 1
Средняя линия треугольника
Определение. Средняя линия треугольника — отрезок, соединяющий середины двух сторон треугольника.
Свойства средней линии треугольника
1. Любой треугольник имеет три средних линии
2. Средняя линия треугольника параллельна основанию и равна его половине.MN = 12AC KN = 12AB KM = 12BC
MN || AC KN || AB KM || BC
3. Средняя линия отсекает треугольник, подобный данному, площадь которого равна четвёрти площади исходного треугольникаS∆MBN = 14 S∆ABC
S∆MAK = 14 S∆ABC
S∆NCK = 14 S∆ABC
4. При пересечении всех трёх средних линий образуются 4 равных треугольника, подобных (даже гомотетичных) исходному с коэффициентом 1/2.∆MBN ∼ ∆ABC
∆AMK ∼ ∆ABC
∆KNC ∼ ∆ABC
∆NKM ∼ ∆ABC
Признаки. Если отрезок параллелен одной из сторон треугольника и соединяет середину стороны треугольника с точкой, лежащей на другой стороне треугольника, то этот отрезок — средняя линия.
Периметр треугольника
Периметр треугольника ∆ABC равен сумме длин его сторон
P = a + b + c
Формулы площади треугольника
- Формула площади треугольника по стороне и высоте
Площадь треугольника равна половине произведения длины стороны треугольника на длину проведенной к этой стороне высотыS = 12a · ha
S = 12b · hb
S = 12c · hc - Формула площади треугольника по трем сторонам
Формула Герона
S = √p(p — a)(p — b)(p — c)
где p = a + b + c2 — полупериметр треугльника.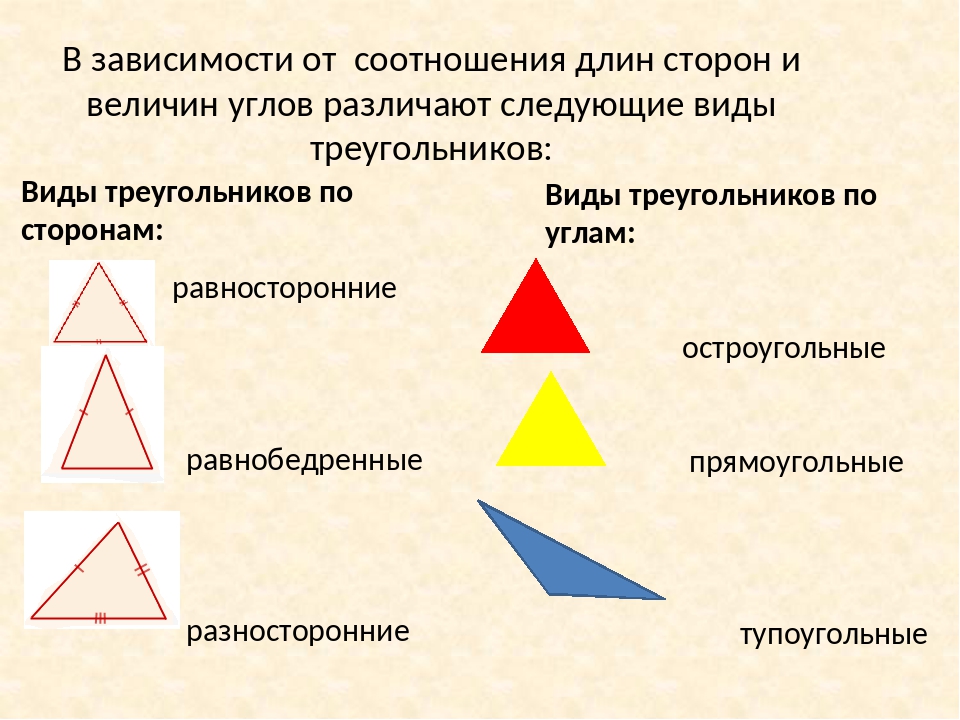
- Формула площади треугольника по двум сторонам и углу между ними
Площадь треугольника равна половине произведения двух его сторон умноженного на синус угла между ними.S = 12a · b · sin γ
S = 12b · c · sin α
S = 12a · c · sin β - Формула площади треугольника по трем сторонам и радиусу описанной окружности
- Формула площади треугольника по трем сторонам и радиусу вписанной окружности
Площадь треугольника равна произведения полупериметра треугольника на радиус вписанной окружности.
Равенство треугольников
Определение. Если два треугольника АВС и А1В1С1 можно совместить наложением, то они равны.
Свойства. У равных треугольников равны и их соответствующие элементы. (В равных треугольниках против равных сторон лежат равные углы, против равных углов лежат равные стороны)
Признаки равенства треугольников
Теорема 1.
Первый признак равенства треугольников — по двум сторонам и углу между ними
Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.Теорема 2.
Второй признак равенства треугольников — по стороне и двум прилежащим углам
Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.Теорема 3.
Третий признак равенства треугольников — по трем сторонам
Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны.Подобие треугольников
Определение. Подобные треугольники — треугольники соответствующие углы которых равны, а сходственные стороны пропорциональны.∆АВС ~ ∆MNK => α = α1, β = β1, γ = γ1 и ABMN = BCNK = ACMK = k,
где k — коэффициент подобияПризнаки подобия треугольников
Первый признак подобия треугольников
Если два угла одного треугольника соответственно равны двум углам другого, то такие треугольники подобны.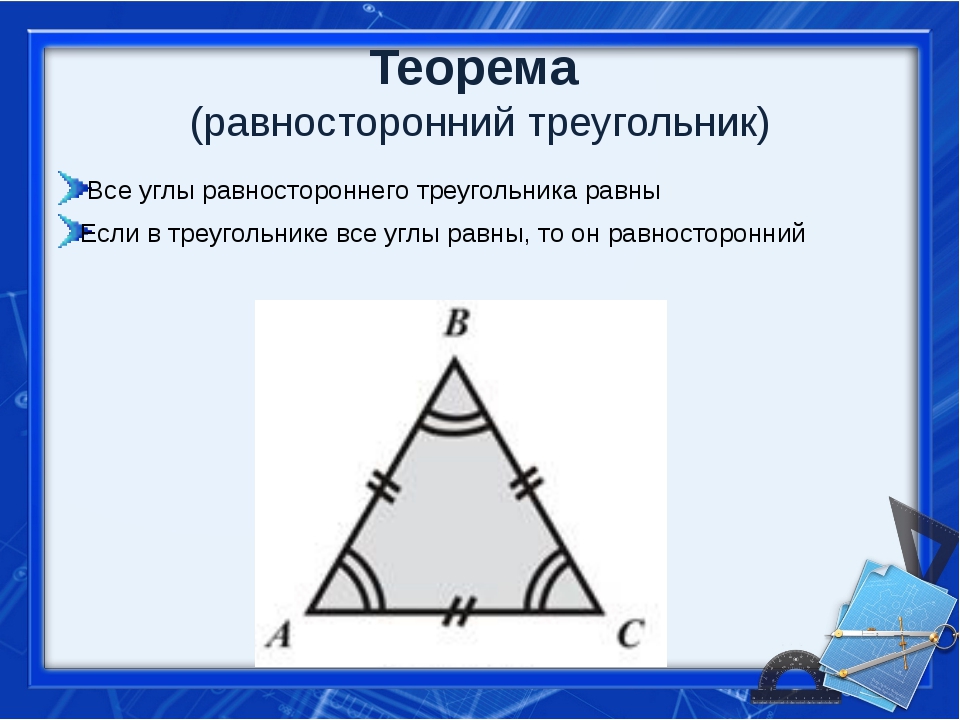
Второй признак подобия треугольников
Если три стороны одного треугольника пропорциональны трем сторонам другого, то такие треугольники подобны.Третий признак подобия треугольников
Если две стороны одного треугольника пропорциональны двум сторонам другого, а углы, между этими сторонами, равны, то такие треугольники подобны. Свойства. Площади подобных треугольников относятся как квадрат коэффициента подобия:S∆АВСS∆MNK = k2
Вписанный и описанный треугольник — материалы для подготовки к ЕГЭ по Математике
Вписанный треугольник — треугольник, все вершины которого лежат на окружности. Тогда окружность называется описанной вокруг треугольника.
Очевидно, расстояние от центра описанной окружности до каждой из вершин треугольника одинаково и равно радиусу этой окружности.
Вокруг любого треугольника можно описать окружность, причем только одну.
Окружность вписана в треугольник, если она касается всех его сторон. Тогда сам треугольник будет описанным вокруг окружности. Расстояние от центра вписанной окружности до каждой из сторон треугольника равно радиусу этой окружности.
В любой треугольник можно вписать окружность, причем только одну.
Попробуйте сами описать окружность вокруг треугольника и вписать окружность в треугольник.
Как вы думаете, почему центр вписанной окружности — это точка пересечения биссектрис треугольника, а центр описанной окружности — точка пересечения серединных перпендикуляров к его сторонам?
В задачах ЕГЭ чаще всего встречаются вписанные и описанные правильные треугольники.
Есть и другие задачи. Для их решения вам понадобятся еще две формулы площади треугольника, а также теорема синусов.
Вот еще две формулы для площади.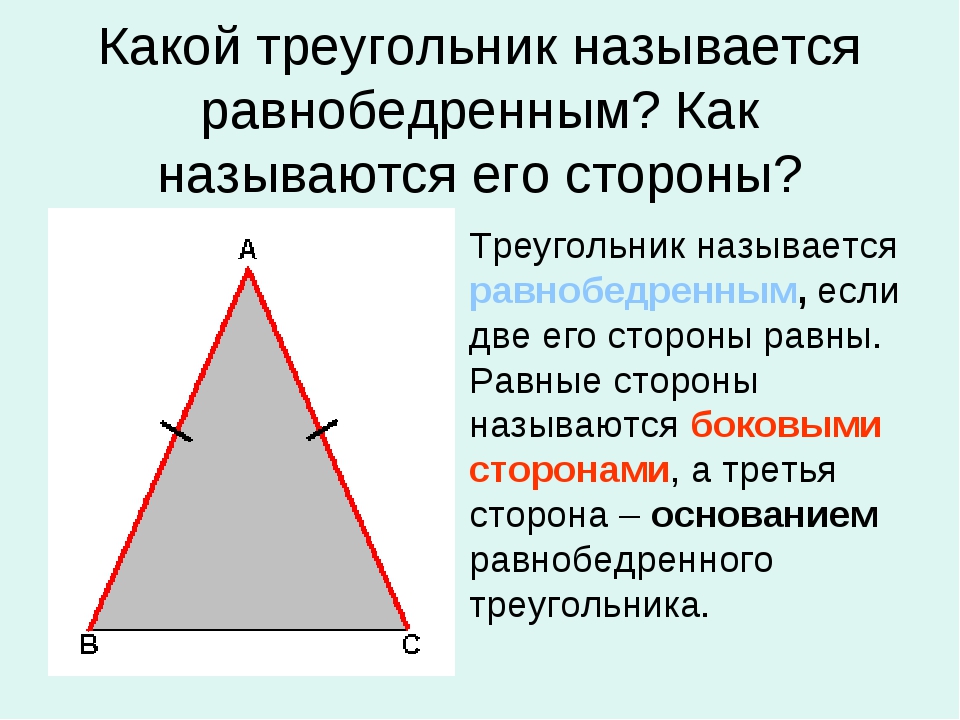
Площадь треугольника равна половине произведения его периметра на радиус вписанной окружности.
,
где — полупериметр,
— радиус окружности, вписанной в треугольник.
Есть и еще одна формула, применяемая в основном в задачах части :
где — стороны треугольника, — радиус описанной окружности.
Для любого треугольника верна теорема синусов:
Ты нашел то, что искал? Поделись с друзьями!
. Радиус окружности, вписанной в равнобедренный прямоугольный треугольник, равен . Найдите гипотенузу c этого треугольника. В ответе укажите .
Треугольник прямоугольный и равнобедренный. Значит, его катеты одинаковы. Пусть каждый катет равен . Тогда гипотенуза равна .
Запишем площадь треугольника АВС двумя способами:
Приравняв эти выражения, получим, что . Поскольку , получаем, что . Тогда .
В ответ запишем .
Ответ: .
. Сторона АС треугольника АВС с тупым углом В равна радиусу описанной около него окружности.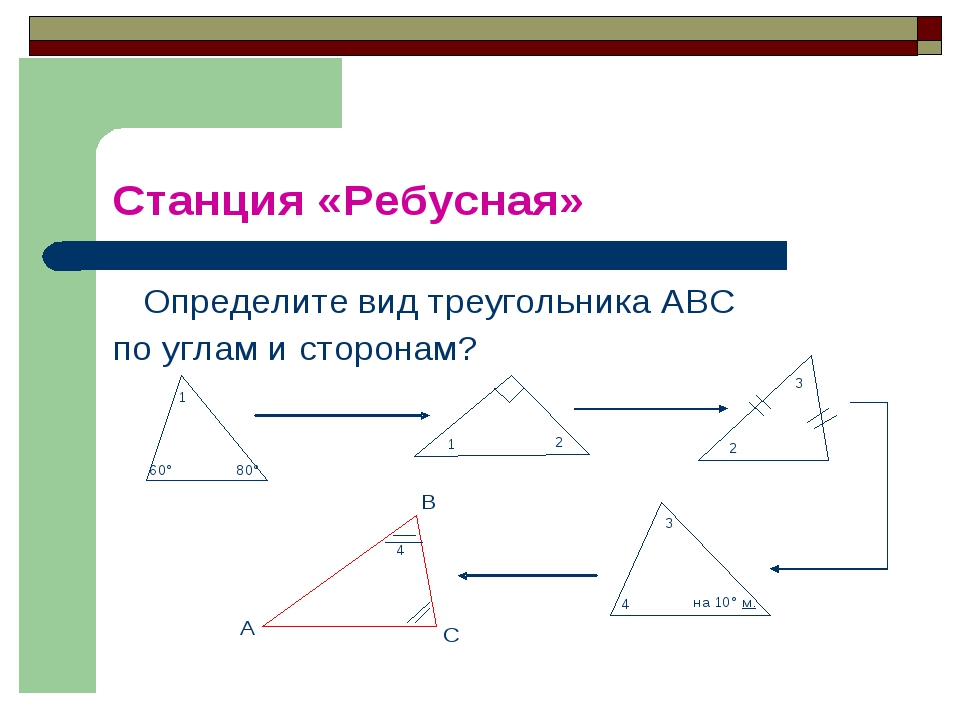 Найдите угол В. Ответ дайте в градусах.
Найдите угол В. Ответ дайте в градусах.
По теореме синусов,
Получаем, что . Угол — тупой. Значит, он равен .
Ответ: .
. Боковые стороны равнобедренного треугольника равны , основание равно . Найдите радиус описанной окружности этого треугольника.
Углы треугольника не даны. Что ж, выразим его площадь двумя разными способами.
, где — высота треугольника. Ее найти несложно — ведь в равнобедренном треугольнике высота является также и медианой, то есть делит сторону пополам. По теореме Пифагора найдем . Тогда .
Задачи на вписанные и описанные треугольники особенно необходимы тем, кто нацелен на решения задания .
Фронтовые письма-треугольники: «Покажем, как русские воюют!» — Из жизни
Материал подготовлен Рузским ИА>>
Через месяц Россия будет отмечать День Победы. Это особый праздник, ведь в далеком 1945 году 9 мая ознаменовало завершение Великой Отечественной войны, которая унесла столько жизней. Иногда от павших в боях остаются только фронтовые треугольники. Житель поселка Тучково Виктор Румынин всю жизнь хранит письма отца и старшего брата, которые погибли в боях с фашистами. Корреспондент Рузского информагентства прочитала их и узнала, о чем писали солдаты, что их волновало, на что они надеялись.
Иногда от павших в боях остаются только фронтовые треугольники. Житель поселка Тучково Виктор Румынин всю жизнь хранит письма отца и старшего брата, которые погибли в боях с фашистами. Корреспондент Рузского информагентства прочитала их и узнала, о чем писали солдаты, что их волновало, на что они надеялись.
Дети блокады – про оборону Ленинграда, «дуранду» и первую любовь>>
Фронтовые треугольники
Фото: Сергей Савиных, Рузское ИА
Больше 70 лет в семье Виктора Алексеевича Румынина, жителя подмосковного поселка Тучково, хранятся фронтовые письма его отца Алексея Ивановича и старшего брата Владимира. Три треугольничка, доставленных полевой почтой с 1941 по 1944 годы. В них звучат горечь от разлуки с родными, беспокойство о них, уверенность в победе над врагом, надежда на возвращение домой.
Когда началась Великая Отечественная война, у Феклы Лукиничны и Алексея Ивановича Румыниных было семеро детей: три дочери и четыре сына. Старшему Володе исполнилось 17 лет, а младшему Вите – всего три месяца. Семья жила в селе Шпикулово Тамбовской области, была дружной и трудолюбивой.
Старшему Володе исполнилось 17 лет, а младшему Вите – всего три месяца. Семья жила в селе Шпикулово Тамбовской области, была дружной и трудолюбивой.
Известие о нападении немцев на СССР застало Румыниных в гостях в соседней деревне. В тот солнечный день ничто не предвещало беды: люди трудились в поле или на огороде, другие рыбачили, третьи отдыхали. Услышав по радио страшное сообщение, Румынины сразу вернулись домой.
Вскоре Алексея Ивановича забрали на фронт. В семье сохранилось лишь одно его письмо (авторская орфография сохранена):
Фото: Сергей Савиных, Рузское ИА
«Добрый день или вечер!
Здравствуйте, дорогая моя семья: Фекла, Володя, Нюра, Рая, Коля, Валя, Толя и Витя. Кланяюсь вам низко-пренизко и с любовью несколько раз целую вас и желаю всего хорошего на белом свете.
Дорогая Фекла, я сейчас нахожусь около фронта в полевом госпитале. Лечим раненых лошадей. Нас, старичков, отобрали, а молодых отправили на фронт. Мы будем двигаться – куда фронт, туда и мы. Сейчас ничего, а до этого времени было очень трудно. А сейчас хорошо.
Мы будем двигаться – куда фронт, туда и мы. Сейчас ничего, а до этого времени было очень трудно. А сейчас хорошо.
Фекла и Володя! Живите пока как вам там видней и лучше. Если есть хлеб продажный, то покупайте.
Еще передайте привет всем родным и знакомым. Еще поклонитесь Алексею Михайловичу со всей семьей.
Мой адрес: действующая армия, полевая почта, стан/679, п/я №59.1.10.41 г.»
В 1942 году на Алексея Ивановича пришла похоронка.
Ветеран Петр Никишин — боец легендарной партизанской бригады>>
Дорогая мама…
Фото: Сергей Савиных, Рузское ИА
Не успела Фекла Лукинична оправиться после смерти мужа, как повестку на фронт получил ее старший сын Владимир. И потянулись долгие дни, месяцы и годы переживаний за него. Материнское сердце радостно замирало, когда от сына приходила весточка. Он сообщал, что жив и здоров, что вместе с однополчанами гонит врага с нашей земли и надеется на скорую победу:
«Привет с фронта!
Здравствуйте многоуважаемая мама, братья и сестры, все родные и знакомые, шлю вам свой фронтовой воинский привет и много наилучших пожеланий в вашей домашней жизни.
Дорогая мама. Я вас прошу, чтоб вы написали, как посадили свой огород, кто вам помогал. Вы мне это все пропишите и потом еще пропишите, кто работал директором и механиком в мастерской, передавайте им мой фронтовой привет и привет от всего моего взвода как нашим помощникам фронта. Сейчас фронт и тыл считаются единой семьей, охваченной одной мыслью – мщения немецким извергам.
Дорогая мама, это все я пишу с великой гордостью, потому что мы здесь валим и бьем врага, как били до нас передовые части нашей молодой гвардии. Мама, еще я пропишу, как живу. Живу я пока хорошо. Может быть, будем живы до окончания войны.
Дорогая мама, вы обо мне особо не беспокойтесь, я здесь живу очень хорошо, скоро зайдем на чужую территорию.
Дорогая мама, я вас прошу, чтобы вы прислали мне адрес Коли Румынина, Пети и Вани Шапкиных. Я буду сам вести с ними переписку. Что, брат Саня, пишет вам письма или нет? Я потерял с ним связь. Вы сами знаете, когда нету писем, то очень плохо, сердце стонет, а как получишь ответ, то сразу веселей, вот так и мне здесь. 23.05.1944 г.»
23.05.1944 г.»
Фото: Сергей Савиных, Рузское ИА
Проводив на войну сына и мужа, Фекла Лукинична, инвалид второй группы, осталась одна с шестью детьми. Отец, уходя на фронт, просил дочерей: «Девки, не забывайте ребят». Все тяготы трудовой жизни легли на хрупкие детские плечи четырнадцатилетней Анюты и двенадцатилетней Раисы. Раиса училась в школе и подрабатывала уборщицей и сторожем в конторе. Там было семь печей, для которых надо было рубить и пилить дрова.
Как потом вспоминала Раиса Алексеевна, был страшный голод. Хлеб выдавали на каждого по кусочку размером со спичечный коробок. Во время уборочной у детей проверяли рот, чтобы они не укрыли зерно за щекой. По ночам девочки ездили за мерзлой свеклой – днем было некогда, да и не разрешали. Как только с полей сходил снег, подбирали мерзлую червивую картошку. Ее грели на раскаленной сковороде, чтобы выползли черви, после чего из нее пекли лепешки пополам с лебедой.
По вечерам младшие Румынины делали уроки при свете керосиновой лампы. Школа зимой не отапливалась, чернила замерзали, их отогревали, а потом писали, не снимая варежек, на клочках бумаги – тетрадей не было.
Школа зимой не отапливалась, чернила замерзали, их отогревали, а потом писали, не снимая варежек, на клочках бумаги – тетрадей не было.
Ветеран из Пушкина Анастасия Катомина: «Партизанская юность моя»>>
Покажем, как русские воюют!
Фото: Сергей Савиных, Рузское ИА
Настоящим праздником было, когда в дом Румыниных приходили письма от Володи. Фекла Лукинична дрожащими руками осторожно раскрывала фронтовые треугольнички. Сама читать не могла – мешали слезы. Отдавала Анюте или Раисе.
В письме от 12 декабря 1944 года Владимир прислал свои стихи:
«Письмо от сына матери
Ты пишешь мне, что поседел твой волос,
Что ждешь меня. Разлуки долог срок…
Я узнаю твой материнский голос
В живом дыханье задушевных строк.
Любовь твоя не ведает предела.
И в каждом слове чувствую тебя,
На чьих глазах и юность отшумела,
И зрелой стала молодость моя
И мне тяжка трехлетняя разлука,
Когда я дни былые вспомяну,
Тебя, мама, братьев, сестер, любимую подругу,
Товарищей, ушедших на войну,
Родной наш дом. Как все это знакомо!
Как все это знакомо!
Я не один ушел из дома,
а вместе с папой.
И с грустью думаю о нем.
Крепись и жди, недолго ждать осталось.
Настанет день, утихнет грозный бой.
И все, о чем так трепетно мечталось,
Взойдет над миром вешнею зарей.
Пока ж войны еще бушует пламя,
С тобою рядом быть я не могу.
И шлю тебе стихи свои на память,
И клятву быть безжалостным к врагу.
Не усмирит никто мой гнев мятежный,
Пока врагу не отплачу сполна
За каждый вздох, за каждый волос нежный,
За всех, о ком грустишь ты не одна.
И вот стихам моим конец. Ваш сын Румынин В.А.
Фото: Сергей Савиных, Рузское ИА
Теперь продолжу свое письмо. В первых строках я спешу передать свой привет всем вам и спешу сообщить, что ваших писем получил штук пять, и во всех вы просите мое фото. И я оправил вам его. Если не получите, напишите мне, я вышлю вам еще фото.
Дорогая мама, вы пишете, что живете хорошо. Это неплохо. Но пропишите, из-за чего вам трудно.
Я живу пока по-старому. Накануне опять на фронте старался быстрей добить коварного зверя в его собственной берлоге. Мама, обо мне не беспокойся, за меня вам краснеть не придется, я благодарю вас за свое воспитание. Я здесь отношусь так, как подобает нашему воину рабоче-крестьянской Красной Армии.
Дорогая мама, вы мне давали наказ, когда я уходил в армию, без пощады бить немца, и мы сейчас ему покажем, как русские воюют. Он хотел с гармошкой завоевать Россию, но он сейчас забыл все свои гармошки.
Письмо писать кончаю. Жду ответа, как соловей лета.
Передаю мои личные приветы директору и рабочим МТС, родным и друзьям».
Володя воевал храбро. Не зря сержанту Румынину за отличные боевые действия приказом Верховного Главнокомандующего Маршала Советского Союза И. В. Сталина были объявлены благодарности за отличные боевые действия по овладению городом Брест, за прорыв обороны немцев на плацдарме на западном берегу реки Нарев севернее Варшавы, за овладение городом Модлин (Новогеоргиевск).
Ветеран-артиллерист Анатолий Пенкин: три фронта и три медали «За отвагу»>>
Письмо от незнакомого бойца
Фото: Сергей Савиных, Рузское ИА
Война подходила к концу, и Фекла Лукинична с нетерпением ждала, когда же увидит и обнимет своего сына. Однако вместо этого за полтора месяца до победы получила похоронку. В ней значилось: «Ваш сын артмастер сержант Румынин Владимир Алексеевич в бою за социалистическую Родину, верный воинской присяге, проявив геройство и мужество, был убит 29 марта 1945 года и похоронен с отданием воинских почестей на городском кладбище г. Цопот (Польша)».
Вскоре Румынины получили письмо от однополчанина Владимира (авторская орфография сохранена):
«Привет с фронта!
Здравствуйте Фекла Лукинична! Примите фронтовой привет от незнакомого вам бойца. Фекла Лукинична, ваш сын Владимир Румынин, а мой друг, с которым мы вместе спали и ели, погиб смертью храбрых в боях за нашу советскую Родину с немецкими гадами. Ну, ничего, Фекла Лукинична, не расстраивайтесь, мы ему поклялись отомстить немецким гадам втрижды за нашего боевого товарища Владимира Румынина. Высылаю вам его фотографии и благодарности.
Жду ответа.
Фекла Лукинична, я еще вам напишу, как мы его похоронили. Сделали ему гроб, покрасили, похоронили Владимира на берегу Балтийского моря у г. Цопот на городском кладбище. Погиб он во время бомбежки. Что еще вас интересует, пишите».
Фото: Сергей Савиных, Рузское ИА
После войны Аня, Рая, Валя и Коля Румынины остались жить в родном Шпикулове. Анна выучилась на портного, Раиса 42 года проработала бухгалтером, Валентина стала поваром в детском саду, Николай – комбайнером. Анатолий Румынин после окончания Борисоглебского дорожного техникума уехал в город Невель. Виктор после Горьковского ракетного училища дослужился до полковника. Фекла Лукинична прожила долгую жизнь и каждый день вспоминала своего мужа и сына, бережно храня их фронтовые письма.
Ветеран Николай Марков из Подмосковья: тысяча дней до Победы>>
Галина Белозерова
треугольников (предварительная алгебра, введение в геометрию) — Mathplanet
Треугольник состоит из трех отрезков прямых. Сегменты линии пересекаются в своих конечных точках. Чтобы назвать треугольник, мы часто используем его вершины (название конечных точек). Треугольник ниже называется ABC.
У треугольника три угла. Сумма углов всегда равна 180 ° в треугольнике.
У нас есть разные типы треугольников. Треугольник классифицируется по углам и количеству совпадающих сторон.
Треугольник с тремя острыми ангелами называется острым треугольником.
Треугольник с одним прямым углом называется прямоугольным.
Треугольник с одним тупым углом называется тупым треугольником.
Когда треугольник имеет три равные стороны, мы называем его равносторонним треугольником. Отметим совпадающие стороны косой чертой. Углы в равностороннем треугольнике всегда равны 60 °.
Если у треугольника две равные стороны, он называется равнобедренным треугольником.Углы, противоположные двум сторонам одинаковой длины, совпадают.
Треугольник без равных сторон или углов называется разносторонним треугольником.
Когда два треугольника совпадают, это означает, что они имеют одинаковый размер и форму. Это означает, что у них одинаковые углы. Красные косые черты показывают нам, какие стороны и углы совпадают. Конгруэнтность показана этим символом
.$$ \ cong $$
$$ \ begin {matrix} A \ cong X & & AB \ cong XY \\ B \ cong Y & & BC \ cong YZ \\ C \ cong Z & & AC \ cong XZ \ end {matrix} $$
Треугольники с одинаковыми углами, но не одинакового размера, называются подобными.Подобные треугольники имеют пропорциональные стороны. Сходство обозначается этим символом
$$ \ sim $$
$$ \ bigtriangleup ABC \ sim \ bigtriangleup XYZ $$
$$ A = X, \: \: B = Y, \: \: C = Z $$
$$ \ frac {a} {x} = \ frac {b} {y} = \ frac {c} {z} $$
Пример
Найдите x в подобных треугольниках.
Мы знаем, что, поскольку треугольники похожи, стороны пропорциональны, что означает, что
$$ \ frac {x} {14} = \ frac {3} {21} \ Rightarrow $$
$$ x = \ frac {14 \ cdot 3} {21} = \ frac {42} {21} = 2 $$
$$ x = 2 $$
Видеоурок
Определите, какие треугольники прямые, равнобедренные, острые, разносторонние, тупые или равносторонние
Что такое треугольник? — [Определение, факты и примеры]
Triangle Games
Типы треугольниковКлассифицируйте треугольники на основе длин сторон и углов.Ищите острые, тупые и прямые углы и определяйте равные стороны.
охватывает Common Core Curriculum 4.G.2Играть сейчасПосмотреть все игры по геометрии >>Учитесь с помощью полной программы обучения математике K-5
Что такое треугольник?
В геометрии треугольник — это замкнутая двумерная форма с тремя прямыми сторонами. Треугольник — это тоже многоугольник.
Мы можем найти форму треугольника в флаге, треугольнике музыкального инструмента и придорожной вывеске.
Свойства треугольника- Треугольник имеет три стороны, три вершины и три угла.
- Сумма трех внутренних углов треугольника всегда равна 180 °.
- Сумма длины двух сторон треугольника всегда больше, чем длина третьей стороны.
- Треугольник с вершинами P, Q и R обозначается как △ PQR.
- Площадь треугольника равна половине произведения его основания и высоты.
Чтобы классифицировать треугольники по их углам, мы измеряем каждый из его внутренних углов. Треугольники можно классифицировать по углам, как:
Острый треугольник имеет все внутренние углы острые (менее 90 °), прямоугольный треугольник имеет один прямой угол (равный 90 °), а тупой треугольник имеет один тупой угол (более 90 °).
Чтобы классифицировать треугольники по их сторонам, мы измеряем длину каждой из его сторон. Треугольники можно классифицировать по сторонам:
Чтобы классифицировать треугольники по углам и сторонам, мы измеряем внутренние углы и длину сторон треугольника. Вот несколько примеров треугольников, классифицируемых как по углам, так и по сторонам:
|
Интересные факты
|
Давайте споем!
Дженна любит треугольники!
Крошечные треугольники на блузке,
Красная крыша ее кукольного домика,
Кусок сыра для ее мышки.
Давайте сделаем это!
Вместо того, чтобы раздавать своим детям рабочие листы по математике, попросите ребенка наблюдать / определять предметы треугольной формы.
Вы также можете дать им зубочистки или соломинки и попросить их сформировать из них самые разные треугольники.
Сопутствующая математическая лексика —
Triangle Proofs — Common Core: High School
Если вы считаете, что контент, доступный через Веб-сайт (как определено в наших Условиях обслуживания), нарушает или несколько ваших авторских прав, сообщите нам, отправив письменное уведомление («Уведомление о нарушении»), содержащее в информацию, описанную ниже, назначенному ниже агенту.Если репетиторы университета предпримут действия в ответ на ан Уведомление о нарушении, оно предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.
Ваше Уведомление о нарушении прав может быть отправлено стороне, предоставившей доступ к контенту, или третьим лицам, таким как в виде ChillingEffects.org.
Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатам), если вы существенно искажать информацию о том, что продукт или действие нарушает ваши авторские права.Таким образом, если вы не уверены, что контент находится на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу.
Чтобы отправить уведомление, выполните следующие действия:
Вы должны включить следующее:
Физическая или электронная подпись правообладателя или лица, уполномоченного действовать от их имени; Идентификация авторских прав, которые, как утверждается, были нарушены; Описание характера и точного местонахождения контента, который, по вашему мнению, нарушает ваши авторские права, в \ достаточно подробностей, чтобы позволить репетиторам университетских школ найти и точно идентифицировать этот контент; например нам требуется а ссылка на конкретный вопрос (а не только на название вопроса), который содержит содержание и описание к какой конкретной части вопроса — изображению, ссылке, тексту и т. д. — относится ваша жалоба; Ваше имя, адрес, номер телефона и адрес электронной почты; и Ваше заявление: (а) вы добросовестно полагаете, что использование контента, который, по вашему мнению, нарушает ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство, что вы либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.
Отправьте жалобу нашему уполномоченному агенту по адресу:
Чарльз Кон
Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105
Или заполните форму ниже:
Треугольник — Лаборатория сценариев
ТРЕУГОЛЬНИК
Мы все можем представить себе треугольник: три линии, три точки, три угла. А изображение треугольника — отличный способ задуматься о процессе письма.Всегда есть три части: писатель, материал и аудитория.
Но часто писатели виноваты в линейном исполнении своей работы. Когда писателя интересует только материал, всегда есть вероятность фатальных ошибок в повествовании.
Представьте, что вы проводите горизонтальную линию между писателем и предметом или материалом рассказа. Отношения очень прямые, интенсивные и простые, но очень часто конечный продукт пишется только одному человеку: самому писателю.
Чтобы избежать этого, мы должны думать о письме как о треугольнике: писатель под одним углом, материал рассказа под другим, а аудитория под конечным углом.
Всегда есть три части. Писатель должен учитывать свои отношения с материалом и аудиторией, а также исследовать, как материал повлияет на его / ее аудиторию. Проще говоря, писатель пишет для аудитории; следовательно, на решения, которые он / она принимает при представлении истории, влияет то, как он / она хочет, чтобы аудитория чувствовала себя.
Писатель хочет, чтобы аудитория удивлялась неожиданному, или умно, позволяя им соединять точки? Иногда писатель хочет, чтобы аудитория открывала для себя вместе с персонажем, иногда мы учимся раньше персонажа, а иногда мы узнаем об этом последними.
Невозможно принимать разумные решения, если писатель не сосредоточен на полном треугольнике: писатель, материал и аудитория.
Мы все можем представить себе треугольник: три линии, три точки, три угла.А изображение треугольника — отличный способ задуматься о процессе письма. Всегда есть три части: писатель, материал и аудитория.
Но часто писатели виноваты в линейном исполнении своей работы. Когда писателя интересует только материал, всегда есть вероятность фатальных ошибок в повествовании.
Представьте, что вы проводите горизонтальную линию между писателем и предметом или материалом рассказа. Отношения очень прямые, интенсивные и простые, но очень часто конечный продукт пишется только одному человеку: самому писателю.
Чтобы избежать этого, мы должны думать о письме как о треугольнике: писатель под одним углом, материал рассказа под другим, а аудитория под конечным углом.
Всегда есть три части. При написании сценария писатель должен учитывать свои отношения со сценарием, а также исследовать, как сценарий повлияет на его / ее аудиторию. Проще говоря, писатель пишет для аудитории; следовательно, на решения, которые он / она принимает при представлении истории, влияет то, как он / она хочет, чтобы аудитория чувствовала себя.
Писатель хочет, чтобы аудитория удивлялась неожиданностям, или умно, позволяя им соединять точки? Иногда писатель хочет, чтобы аудитория открывала для себя вместе с персонажем, иногда мы учимся раньше персонажа, а иногда мы узнаем об этом последними.
Невозможно принимать разумные решения, если писатель не сосредоточен на полном треугольнике: писатель, рассказ и аудитория.
Что такое треугольник и его свойства? Определение, виды, формулы треугольников
В этой статье мы узнаем о простейшей форме многоугольника: треугольник .Все многоугольники можно разделить на треугольники, или, другими словами, они образованы путем объединения двух или более треугольников. Таким образом, важно понимать основные свойства треугольника и их типы.
Вот краткое описание тем, которые мы рассмотрим в этой статье:
Вы также можете просмотреть это видео о свойствах треугольника:
Что такое треугольник?
Как следует из названия, треугольник представляет собой многоугольник с тремя углами.Итак, когда у замкнутой фигуры три угла?
Когда он состоит из трех отрезков, соединенных встык.
Таким образом, мы можем сказать, что треугольник — это многоугольник, у которого есть три стороны, три угла, три вершины, а сумма всех трех углов любого треугольника равна 180 °.
Свойства треугольника
Свойства треугольника:
- Треугольник имеет три стороны, три угла и три вершины.
- Сумма всех внутренних углов треугольника всегда равна 180 °. Это называется свойством суммы углов треугольника.
- Сумма длин любых двух сторон треугольника больше, чем длина третьей стороны.
- Сторона, противоположная наибольшему углу треугольника, является наибольшей стороной.
- Любой внешний угол треугольника равен сумме его внутренних противоположных углов. Это называется свойством внешнего угла треугольника.
Виды треугольников
Треугольники можно классифицировать двумя основными способами:
- Классификация по внутренним углам
- Классификация по длине сторон
Классификация треугольника по внутренним углам
На основании измерения угла различают три типа треугольников:
- Острый угловой треугольник
- Прямоугольный треугольник
- Тупоугольный треугольник
Давайте подробно обсудим каждый тип.
Острый угловой треугольник
Треугольник, у которого всех трех углов меньше 90 °, является треугольником с острыми углами.
- Итак, все углы треугольника с острыми углами называются острыми углами
Ниже приведен пример треугольника с острыми углами.
Прямоугольный треугольник
Треугольник с углом и точным размером 90 ° является прямоугольным треугольником.
- Два других угла прямоугольного треугольника являются острыми углами.2
Это известно как Теорема Пифагора
Наоборот, мы можем сказать, что если треугольник удовлетворяет условию Пифагора, то это прямоугольный треугольник.
Тупой / наклонный угловой треугольник
Треугольник с углом и более ° является треугольником с тупым углом.
Ниже приведен пример треугольника с тупым / наклонным углом.
Вопросы о треугольниках очень часто задают на GMAT.Ace GMAT Quant, подписавшись на бесплатную пробную версию, вы получите доступ к более чем 400 вопросам. Мы являемся самой популярной онлайн-компанией по подготовке к GMAT с более чем 2060 отзывами на GMATClub.
Учитесь у Гильермо, который улучшился с Q38 до Q50.
Классификация треугольников по длине сторон
В зависимости от длины сторон треугольники подразделяются на три типа:
- Масштабный треугольник
- Равнобедренный треугольник
- Равносторонний треугольник
Давайте подробно обсудим каждый тип.
Чешуйчатый треугольник
Треугольник, у которого все три стороны разной длины — разносторонний треугольник.
- Поскольку все три стороны имеют разную длину, у три угла также будут разными.
Ниже приведен пример разностороннего треугольника
.Равнобедренный треугольник
Треугольник, у которого две стороны одинаковой длины и третья сторона разной длины , является равнобедренным треугольником.
- Углы напротив равных сторон равны.
Ниже приведен пример равнобедренного треугольника.
Равносторонний треугольник
Треугольник, у которого все три стороны одинаковой длины , является равносторонним треугольником.
- Поскольку все три стороны имеют одинаковую длину, все три угла также будут равны.
- Каждый внутренний угол равностороннего треугольника = 60 °
Особые случаи прямоугольных треугольников
Давайте также рассмотрим несколько частных случаев прямоугольного треугольника
45-45-90 треугольник
В этом треугольнике
- Два угла составляют 45 °, а третий угол является прямым.
- Стороны этого треугольника будут в соотношении — 1: 1: √2 соответственно.
- Его также называют равнобедренным прямоугольным треугольником , поскольку два угла равны.
30-60-90 треугольник
В этом треугольнике
- Это прямоугольный треугольник, так как один угол = 90 °
- Углы этого треугольника находятся в соотношении — 1: 2: 3, а
- Стороны , противоположные этим углам, будут в соотношении — 1: √3: 2 соответственно
- Это разносторонний прямоугольный треугольник , поскольку все три угла разные.
Формула площади треугольника
- Площадь любого треугольника = ½ * основание * высота
- Площадь прямоугольного треугольника = ½ * произведение двух перпендикулярных сторон
Свойства треугольника: сводка и основные выводы
Подведем итог некоторым важным свойствам треугольника.
- Сумма всех внутренних углов любого треугольника равна 180 °
- Сумма всех внешних углов любого треугольника равна 360 °
- Внешний угол треугольник равен сумме двух его внутренних противоположных углов
- Сумма длин любых двух сторон треугольника всегда больше, чем длина третьей стороны
- Аналогично, разница между длинами из любая двух сторон треугольника всегда меньше длины третьей стороны
- Сторона, противоположная наименьшему внутреннему углу, является самой короткой стороной и наоборот.
- Точно так же сторона, противоположная наибольшему внутреннему углу, является самой длинной стороной и наоборот.
- В случае прямоугольного треугольника эта сторона называется гипотенузой
- Высота треугольника равна длине перпендикуляра, опущенного из вершины на противоположную сторону, и эта сторона равна считается базовым
Если вам понравилась эта статья, вы также можете прочитать следующие статьи продвинутого уровня о треугольниках
Планируете ли вы поступить в бизнес-школу США? Позвольте нам помочь вам пройти первый этап процесса i.е., сдавая GMAT. Пройдите бесплатный тест GMAT, чтобы понять свой базовый результат, и начните подготовку к GMAT с нашей бесплатной пробной версии. Мы являемся самой популярной онлайн-компанией по подготовке к GMAT с более чем 2060 отзывами на GMATClub.
Свойства треугольника: тест по применению
Вопрос: 1
В равнобедренном треугольнике DEF, если внутренний угол ∠D = 100 °, то каково значение ∠F?
- 20 °
- 40 °
- 60 °
- 80 °
- 100 °
Раствор
Шаг 1: Дано
- ∆DEF — равнобедренный треугольник
Шаг 2: найти
Шаг 3: подход и разработка
- Мы знаем, что сумма всех внутренних углов в треугольнике = 180 °
- подразумевает, ∠D + ∠E + ∠F = 180 °
- ∠E + ∠F = 180 0 — 100 0 = 80 °
- Так как ∆DEF — равнобедренный треугольник; два его угла должны быть равны.
- И единственная возможность — E = ∠F
- Следовательно, 2∠F = 80 °
- Подразумевается, ∠F = 40 °
Следовательно, правильный ответ — Вариант B.
Вопрос 2
В прямоугольном треугольнике ∆ABC, BC = 26 единиц и AB = 10 единиц. Если BC — самая длинная сторона треугольника, то какова площадь ∆ABC?
- 120
- 130
- 240
- 260
- 312
Раствор
Шаг 1: Дано
- ∆ABC — прямоугольный треугольник
- BC = 26 шт.
- AB = 10 шт.
- до н.э. — самая длинная сторона треугольника
Шаг 2: найти
- Площадь треугольника ∆ABC
Шаг 3: подход и отработка
- Нам дано, что BC — самая длинная сторона треугольника, из чего следует, что BC — гипотенуза
Таким образом, согласно правилу Пифагора:
- BC 2 = AB 2 + AC 2
- 26 2 = 10 2 + AC 2
- AC 2 = 676-100 = 576
- Следовательно, AC = 24 шт.
- Мы знаем, что площадь прямоугольного треугольника = ½ * произведение двух перпендикулярных сторон = ½ * AB * AC = ½ * 10 * 24 = 120 кв.ед.
Следовательно, правильный ответ — Вариант А .
Вот еще несколько статей, которые вы можете прочитать:
FAQ — Свойства треугольника
Что такое треугольник и его свойства?Треугольник — это замкнутая фигура с тремя сторонами, тремя вершинами, тремя углами и суммой внутренних углов 180 °
Какие бывают типы треугольников?Треугольники можно классифицировать двумя способами: по внутренним углам и по длине сторон.По внутренним углам существует три типа треугольников: острый, прямой и тупоугольный. По длине сторон треугольники можно разделить на 3 категории: скален, равнобедренный и равносторонний треугольник.
Что такое треугольник Скален?Треугольник, все три стороны которого различаются по длине, является разносторонним треугольником.
Что такое равнобедренный треугольник?Треугольник, у которого две стороны одинаковой длины и третья сторона разной длины, является равнобедренным треугольником.
Что такое равносторонний треугольник?Треугольник, все три стороны которого имеют одинаковую длину, является равносторонним треугольником.
Как определить, конгруэнтны ли треугольники
Два треугольника равны, если они имеют:
- точно такие же три стороны и
- точно такие же три угла.
Но нам не обязательно знать все три стороны и все три угла… Обычно трех из шести хватает.
Есть пять способов определить, совпадают ли два треугольника: SSS , SAS , ASA , AAS и HL .
1. SSS
(сбоку, сбоку, сбоку)SSS означает «сторона, сторона, сторона» и означает, что у нас есть два треугольника, все три стороны которых равны.
Например:
соответствует: (Дополнительные сведения см. В разделе «Решение треугольников SSS»)
Если три стороны одного треугольника равны трем сторонам другого треугольника, треугольники равны.
2. SAS
(сторона, угол, сторона)SAS означает «сторона, угол, сторона» и означает, что у нас есть два треугольника, у которых, как мы знаем, две стороны и включенный угол равны.
Например:
равно соответствует: (Дополнительные сведения см. В разделе «Решение треугольников SAS»)
Если две стороны и внутренний угол одного треугольника равны соответствующим сторонам и углу другого треугольника, треугольники конгруэнтны.
3.ASA
(угол, сторона, угол)ASA означает «угол, сторона, угол» и означает, что у нас есть два треугольника, из которых мы знаем, что два угла и включенная сторона равны.
Например:
равно соответствует: (Дополнительные сведения см. В разделе «Решение треугольников ASA»)
Если два угла и включенная сторона одного треугольника равны соответствующим углам и стороне другого треугольника, треугольники конгруэнтны.
4. AAS
(угол, угол, сторона)AAS означает «угол, угол, сторона» и означает, что у нас есть два треугольника, из которых мы знаем, что два угла и не включенная сторона равны.
Например:
равно соответствует: (Дополнительные сведения см. В разделе «Решение треугольников AAS»)
Если два угла и сторона без включения одного треугольника равны соответствующим углам и стороне другого треугольника, треугольники совпадают.
5. HL
(гипотенуза, ножка)Это относится только к прямоугольным треугольникам!
или HL означает « H ypotenuse, L eg» (самая длинная сторона прямоугольного треугольника называется «гипотенузой», две другие стороны называются «ногами»)
Это означает, что у нас есть два прямоугольных треугольника с
- одинаковая длина гипотенузы и
- такой же длины для одной из двух других ног .
Неважно, на какой ноге, поскольку треугольники можно вращать.
Например:
равно соответствует: (Подробнее см. Теорему Пифагора)
Если гипотенуза и один катет одного прямоугольного треугольника равны соответствующей гипотенузе и катету другого прямоугольного треугольника, эти два треугольника равны.
Внимание! Не используйте «AAA»
AAA означает, что нам даны все три угла треугольника, но нет сторон.
Этой информации недостаточно, чтобы решить, совпадают ли два треугольника!
Поскольку треугольники могут иметь одинаковые углы, но иметь разных размеров :
— это , а не , совпадающее с: Не зная хотя бы одной стороны, мы не можем быть уверены, совпадают ли два треугольника.
похожих треугольников — математический открытый справочник
подобных треугольников — математический открытый справочникОпределение: треугольники похожи, если имеют одинаковую форму, но могут быть разных размеров.
(Они все еще похожи, даже если один повернут, или один является зеркальным отображением другого).Попробуйте это Перетащите любую оранжевую точку в вершину любого треугольника. Оба треугольника изменят форму и останутся похожими друг на друга.
Треугольники похожи, если они имеют одинаковую форму, но не обязательно одинакового размера. Вы можете думать об этом как о «увеличении» или «уменьшении», увеличивая или уменьшая треугольник, но сохраняя при этом его основную форму. На рисунке выше, когда вы перетаскиваете любую вершину треугольника PQR, другой треугольник принимает ту же форму, но в два раза меньше. В формальных обозначениях мы можем написать
который читается как « Треугольник PQR подобен треугольнику P’Q’R ‘». Буква с небольшой вертикальной чертой после нее, например P ‘, читается как « P prime ».
Свойства подобных треугольников
Соответствующие углы совпадают (одна и та же величина)
Итак, на рисунке выше, угол P = P ‘, Q = Q’ и R = R ‘.Соответствующие стороны имеют одинаковую пропорцию.
Выше PQ вдвое превышает длину P’Q ‘. Следовательно, остальные пары сторон также находятся в той же пропорции. PR вдвое больше P’R ‘, а RQ вдвое больше R’Q’. Формально в двух одинаковых треугольниках PQR и P’Q’R ‘:
Вращение
Один треугольник можно вращать, но пока они одинаковой формы, треугольники остаются похожими.На рисунке ниже треугольник PQR похож на P’Q’R ‘, хотя последний повернут. по часовой стрелке 90 °.
В этом конкретном примере треугольники одинакового размера, поэтому они также конгруэнтный.
Отражение
Один треугольник может быть зеркальным отражением другого, но пока они имеют одинаковую форму, треугольники остаются похожими. Он может отражаться в любом направлении: вверх, вниз, влево, вправо. На рисунке ниже треугольник PQR является зеркальным отображением P’Q’R ‘, но по-прежнему считается похожим на него.Как определить, похожи ли треугольники
Любой треугольник определяется шестью мерками (три стороны, три угла). Но вам не нужно знать их все, чтобы показать, что два треугольника похожи. Подойдут разные группы по три человека. Треугольники подобны, если:- AAA (угол угла)
Все три пары соответствующих углов одинаковы.
См. Похожие треугольники AAA. - SSS в одинаковой пропорции (боковая сторона)
Все три пары соответствующих сторон имеют одинаковую пропорцию
См. Подобные треугольники SSS. - SAS (сторона бокового угла)
Две пары сторон в одинаковой пропорции и равный прилегающий угол.
См. Похожие треугольники SAS.
Подобные треугольники могут иметь общие части
Два треугольника могут быть похожими, даже если у них есть общие элементы. На рисунке ниже больший треугольник PQR аналогичен меньшему STR. S и T — середины PR и QR соответственно. Они разделяют вершину R и часть сторон PR и QR. Они похожи по принципу ААА, поскольку соответствующие углы в каждом треугольнике одинаковы.Другие похожие темы
Похожие полигоны
(C) Открытый справочник по математике, 2011 г.
.
Все права защищены.
