Как найти градиент: Производная по направлению, градиент функции: объяснение, примеры

Содержание

Производная по направлению, градиент функции: объяснение, примеры

Понятие производной по направлению рассматривается для функций двух и трёх переменных. Чтобы понять смысл производной по направлению, нужно сравнить производные по определению

1) функции одной переменной;

2) функции трёх переменных в нашем случае.

Рассматривая функцию одной переменной, мы выяснили, что на оси Oy отображается приращение функции f(x), соответствующее приращению аргумента x. Если мы имеем дело с функцией трёх переменных, то приращения аргументов x, y, z отображаются на осях Оx, Оy, Оz. Сам собой напрашивается вопрос: а где можно отобразить приращение уже не аргументов, а функции трёх переменных?

И вот ответ на этот вопрос: приращение функции трёх переменных отображается на некоторой прямой, направление которой определяется вектором, произвольно заданным в задаче

Если рассматривается функция двух или трёх переменных, то два или три измерения задают аргументы, а упомянутая прямая, на которой отображается приращение функции, — это ещё одно измерение и для его акцентирования назовём это измерение не третьим или четвёртым, а нулевым, следуя программистской традиции (в программировании отсчёт чаще начинается не с единицы, а с нуля).

Для того, чтобы перейти к строгому математическому определению производной по направлению, нужно рассмотреть:

1) функцию u = f(M), определённую в окрестности точки M с координатами x, y, z;

2) произвольный вектор l с направляющими косинусами cosα, cosβ, cosγ.

Через точку M проводим прямую, одно из двух возможных направлений которых совпадает с направлением вектора l. На получившейся прямой отметим точку M1, координаты которой образуют суммы координат точки

M и приращений соответствующих аргументов функции трёх переменных:

Величину отрезка MM1 можно обозначить .

Функция u = f(M) при этом получит приращение

Определение производной по направлению. Предел отношения при , если он существует, называется производной функции u = f(M) по направлению вектора l и обозначается , то есть

Формула, которой нужно пользоваться для нахождения производной по направлению, следующая:

Смысл этой формулы: производная по направлению является линейной комбинацией частных производных, причём направляющие косинусы показывают вклад в производную по направлению соответствующей частной производной.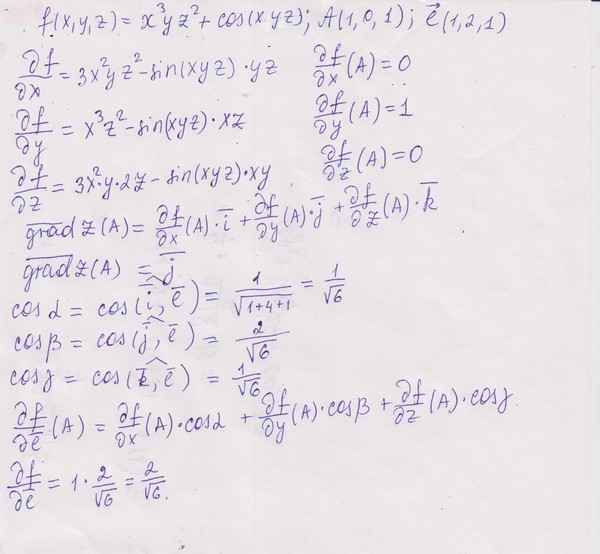

Пример 1. Найти производную функции в точке M0(1; 2; 3) по направлению вектора .

Решение. Найдём

частные производные функции в точке M0:

Найдём направляющие косинусы, пользуясь определением скалярного произведения векторов:

Следовательно,

Теперь можем найти производную по направлению данной функции по её формуле:

А сейчас — домашнее задание. В нём дана функция не трёх, а лишь двух переменных, но несколько иначе задан направляющий вектор. Так что придётся вновь повторить векторную алгебру.

Вектор, задающий направление производной, может быть дан и в такой форме, как в следующем примере — в виде

разложения по ортам координатных осей, но эта хорошо знакомая тема из самого начала векторной алгебры.

Пример 3. Найти производную функции в точке M0(1; 1; 1) по направлению вектора .

Решение. Найдём направляющие косинусы вектора

Найдём частные производные функции в точке M0:

Следовательно, можем найти производную по направлению данной функции по её формуле:

Градиент функции нескольких переменных в точке M0 характеризует направление максимального роста этой функции в точке M0 и величину этого максимального роста.

Как найти градиент?

Нужно определить вектор, проекциями которого на оси координат являются значения частных производных , , этой функции в соответствующей точке:

То есть, должно получиться представление вектора по ортам координатных осей, в котором на каждый орт умножается соответствующая его оси частная производная.

Для градиента функции двух переменных формула короче:

Пример 4. Найти градиент функции в точке M0(2; 4;).

Решение. Найдём частные производные функции в точке M0:

Следовательно, можем записать искомый градиент данной функции:

Поделиться с друзьями

Производные

Функции нескольких переменных

Градиент

Производная по направлению. Градиент

Пусть в некоторой области задана функция и точка . Проведем из точки вектор , направляющие косинусы которого . На векторе , на расстоянии от его начала рассмотрим точку , т.е. .

Будем предполагать, что функция и ее частные производные первого порядка непрерывны в области .

Предел отношения при называется производной от функции в точке по направлению вектора и обозначается , т.е. .

Для нахождения производной от функции в заданной точке по направлению вектора используют формулу: ,

где – направляющие косинусы вектора , которые вычисляются по формулам:
.

Пусть в каждой точке некоторой области задана функция .
Вектор, проекциями которого на оси координат являются значения частных производных этой функции в соответствующей точке, называется градиентом функции и обозначается или (читается «набла у»): .

При этом говорят, что в области определено векторное поле градиентов.

Для нахождения градиента функции в заданной точке используют формулу:
.

Свойства градиента

1. Производная в данной точке по направлению вектора имеет наибольшее значение, если направление вектора совпадает с направлением градиента.

Это наибольшее значение производной равно .

2. Производная по направлению вектора, перпендикулярного к вектору , равна нулю.

Примеры решения задач

Пример 1. Найти производную от функции в точке по направлению вектора .

Решение.

Для решения задачи воспользуемся формулой для нахождения производной от функции в заданной точке по направлению вектора :
,
где – направляющие косинусы вектора , которые вычисляются по формулам:

По условию задачи вектор имеет координаты . Тогда его длина равна:
.

Следовательно, для направляющих косинусов вектора получим следующие значения:
.

Далее для решения задачи необходимо найти все частные производные первого порядка от функции :

Вычислим значения этих частных производных первого порядка в точке :

В заключении подставим полученные значения для направляющих косинусов вектора и значения частных производных первого порядка от функции в точке в формулу для нахождения производной по направлению в заданной точке:

Ответ: производная от функции в точке по направлению вектора равна .

Пример 2. Найти градиент функции в точке .

Решение.

Поскольку градиентом функции называется вектор, проекциями которого на оси координат являются значения частных производных этой функции в соответствующей точке, то для решения задачи сначала найдем все частные производные первого порядка от заданной функции:

Далее вычислим значения этих частных производных первого порядка в точке :

Подставим полученные значения в формулу градиента функции в заданной точке :
.

Ответ: градиент функции в точке равен .

Пример 3. Найти производную функции в точке по направлению градиента функции в той же точке.

Решение.

Для нахождения производной от функции в заданной точке по направлению вектора используют формулу:
,
где – направляющие косинусы вектора , которые вычисляются по формулам:
.

В данном случае вектор совпадает с градиентом функции в точке : .

Следовательно, для решения задачи необходимо найти значения всех частных производных первого порядка от функции в точке , а также координаты и длину градиента функции в той же точке.

Вычислим значения частных производных первого порядка от функции в точке :

Для нахождения координат вектора , равного градиенту функции в заданной точке , вычислим значения частных производных первого порядка от функции в этой точке:

Длина вектора равна: .

Найдем направляющие косинусы вектор по формулам:
.

Подставим полученные значения в формулу для нахождения производной от функции в заданной точке по направлению вектора :

Ответ: производная функции в точке по направлению градиента функции в той же точке равна 1.

Задания для самостоятельной работы

1. Найти производную функции в точке по направлению вектора .
Ответ: .

2. Найти производную функции в точке по направлению вектора .
Ответ: .

3. Найти производную функции в точке по направлению вектора .
Ответ: .

4. Найти градиент функции в точке .
Ответ: .

5. Найти градиент функции в точке .
Ответ: .

6. Найти градиент функции в точке .
Ответ: .

Нахождение градиента вектор-функции

Дата публикации Oct 20, 2018

Название изображения:Источник

ВЧасть 1Нам поставили задачу: вычислить градиент этой функции потерь:

Изображение 1: функция потери

Чтобы найти градиент, мы должны найти производную функцию. ВЧасть 2мы научились вычислять частную производную функции по каждой переменной. Однако большинство переменных в этой функции потерь являются векторами. Возможность найти частную производную векторных переменных особенно важна, поскольку нейронная сеть работает с большими объемами данных. Векторные и матричные операции — это простой способ представления операций с таким большим количеством данных. Как именно вы можете найти градиент вектор-функции?

Градиент скалярной функции

Скажи, что у нас есть функция,f (x, y) = 3x²y, Наши частные производные:

Изображение 2: Частичные производные

Если мы организуем эти части в горизонтальный вектор, мы получимградиентизР (х, у), или∇ f (x, y):

Изображение 3: Градиент f (x, y)

6yxэто изменение вР (х, у)в отношении изменения вИкс, в то время как3x²это изменение вР (х, у)в отношении изменения вY,

Что происходит, когда у нас есть две функции? Давайте добавим еще одну функцию,g (x, y) = 2x + y⁸, Частные производные:

Изображение 4: Частицы для g (x, y)

Таким образом, градиент g (x, y):

Изображение 5: градиент g (x, y)

Представляющие функции

Когда у нас есть несколько функций с несколькими параметрами, часто полезно представлять их более простым способом. Мы можем объединить несколько параметров функций в один векторный аргумент,Иксэто выглядит следующим образом:

Изображение 6: ВекторИкс

Следовательно,Р (х, у, г)станетF (x₁, x₂, x₃)который становитсяе (Икс).

Мы также можем объединить несколько функций в вектор, например так:

Изображение 7: ВекторY

В настоящее время,у = F (X)гдеF (X)является вектором из [f₁ (Икс), f₂ (Икс), f₃ (Икс) … п (Икс)]

Для нашего предыдущего примера с двумя функциями,f (x, y) ⇒ f (Икс)а такжеg (x, y) ⇒ g (Икс).Здесь векторИкс= [x₁, x₂], гдеx₁ = х, а такжеx₂ = у, Чтобы упростить его еще больше, мы можем объединить наши функции: [f (Икс),г(Икс)] = [f₁ (Икс), f₂ (Иксзнак равноf (x) = y.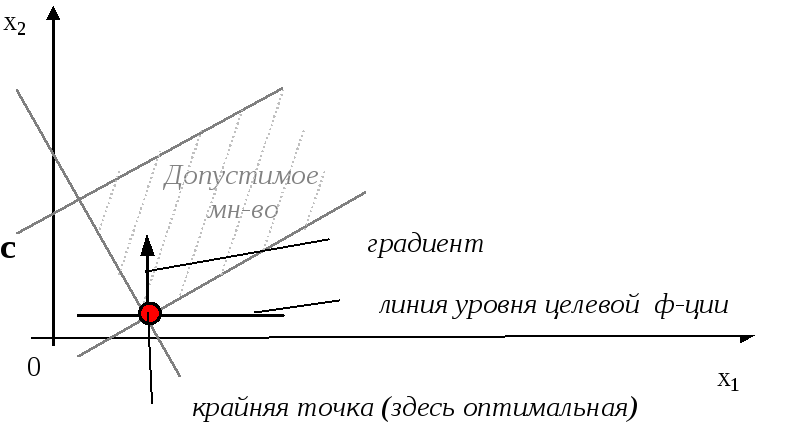

Изображение 8: Уравнения в векторной функцииY

Зачастую количество функций и количество переменных будет одинаковым, поэтому для каждой переменной существует решение.

Градиент вектор-функции

Теперь, когда у нас есть две функции, как мы можем найти градиент обеих функций? Если мы организуем оба их градиента в одну матрицу, мы переместимся из векторного исчисления в матричное исчисление. Эта матрица и организация градиентов нескольких функций с несколькими переменными, известна какМатрица Якобиана,

Изображение 9: Якобиан

Есть несколько способов представления якобиана. Этот макет, где мы укладываем градиенты по вертикали, известен какмакет числителя, но другие документы будут использоватьрасположение знаменателя, который просто переворачивает его по диагонали:

Изображение 10: Расположение знаменателя якобиана

Градиент функции идентичности

Давайте возьмем функцию идентичности,у = ф (х) = х, гдеFi (Икс) = xiи найдите его градиент:

Изображение 11: функция идентификации

Так же, как мы создали наш предыдущий якобиан, мы можем найти градиенты каждой скалярной функции и сложить их вертикально, чтобы создать якобиан тождественной функции:

Изображение 12: Якобиан тождественной функции

Поскольку это функция идентичности, f₁ (Икс) = x₁, f₂ (Икс) = х₂ и тд. Следовательно,

Изображение 13: Якобиан тождественной функции

Частичная производная функции по переменной, которой нет в функции, равна нулю. Например, частная производная 2x² по y равна 0. Другими словами,

Изображение 14: частная производная функции по переменной, которой нет в функции, равна нулю

Поэтому все, что не на диагонали якобиана, становится равным нулю. Между тем, частная производная любой переменной по отношению к себе равна 1. Например, частная производнаяИксв отношенииИксравен 1. Следовательно, якобиан становится:

Изображение 15: Якобиан тождественной функции

Градиент комбинаций вектор-векторных функций

Элементарные бинарные операторыявляются операциями (такими как сложениевес+Иксиливес>Икскоторый возвращает вектор единиц и нулей), который применяет оператор последовательно, начиная с первого элемента обоих векторов, чтобы получить первый элемент вывода, затем второго элемента обоих векторов, чтобы получить второй элемент вывода… и так далее.

Эта статья представляет поэлементные бинарные операции с такими обозначениями:

Изображение 16: Поэлементная двоичная операция с f (x) и g (x)

Здесь ◯ означает любой поэлементный оператор (например, +), а не композицию функций.

Итак, как вы находите градиент поэлементной операции двух векторов?

Поскольку у нас есть два набора функций, нам нужны два якобиана, один из которых представляет градиент относительноИкси один по отношению квес:

Изображение 17: Якобиан по отношению квеса такжеИкс

Большинство арифметических операций нам понадобятся простые, поэтомуе (ш)часто просто векторвес, Другими словами,Fi (Wi) = Wi, Например, операцияW + хподходит к этой категории, так как она может быть представлена каке (ж) + д (х)гдеfi (wi) + gi (xi) = wi + xi.

При этом условии каждый элемент в двух якобианах упрощается до:

Изображение 18: Элементы в якобиане

На диагонали i = j, поэтому существует значение для частной производной. Вне диагонали, однако, i ≠ j, поэтому частные производные становятся равными нулю:

Изображение 19: Диагональный якобиан

Мы можем представить это более кратко как:

Изображение 20: Якобиан по отношению квеса такжеИкс

Попробуем найти градиент функцииW + х, Мы знаем, что все вне диагонали равно 0. Значения частичных по диагонали относительновеса такжеИксявляются:

Изображение 21: Частичное в отношениивеса такжеИкс

Итак, оба якобиана имеют диагональ 1. Это выглядит знакомо … это матрица тождеств!

Давайте попробуем это с умножением:ш * х, Значения частностей по диагонали относительновеса такжеИксявляются:

Изображение 22: Частичное в отношениивеса такжеИкс

Следовательно, градиент по отношению квесизш * хявляетсяDiag (Икс)в то время как градиент по отношению кИксизш * хявляетсяDiag (вес).

Применяя те же шаги для вычитания и деления, мы можем суммировать все это:

Изображение 23: Градиенты общих элементарных бинарных операций

Градиент векторных сумм

Одной из наиболее распространенных операций в глубоком обучении является операция суммирования. Как мы можем найти градиент функцииу = сумма (Икс)?

у = сумма (Икс)также может быть представлен как:

Изображение 24: у = сумма (Икс)

Следовательно, градиент может быть представлен как:

Изображение 25: Градиент у = сумма (Икс)

А так как частная производная функции по переменной, которой нет в функции, равна нулю, ее можно дополнительно упростить следующим образом:

Изображение 26: Градиент у = сумма (Икс)

Обратите внимание, что результатом является горизонтальный вектор.

Как насчет градиентау = сумма (Иксг)? Единственное отличие состоит в том, что мы умножаем каждый частный с константой, z:

Изображение 27: Градиент у = сумма (Икся) в отношенииИкс

Хотя это является производной по отношению кИкс, производная по скаляруZэто просто число:

Изображение 28: Градиент у = сумма (Иксz) относительно z

Градиент комбинаций векторных функций правила цепочки

ВЧасть 2мы узнали о правилах цепей с несколькими переменными. Однако это работает только для скаляров. Давайте посмотрим, как мы можем интегрировать это в векторные вычисления!

Давайте возьмем векторную функцию,Yзнак равное(Икс)и найти градиент. Давайте определим функцию как:

Изображение 29:Yзнак равное(Икс)

И то и другоеf₁ (х)а такжеf₂ (х)являются составными функциями. Введем промежуточные переменные дляf₁ (х)а такжеf₂ (х)и переписать нашу функцию:

Изображение 30:Yзнак равное(г(Икс))

Теперь мы можем использовать наше правило цепочки переменных, чтобы вычислить производную вектораY, Просто вычислите производнуюf₁ (х)а такжеf₂ (х)и поместите их один над другим:

Изображение 31: ГрадиентYзнак равное(г(Икс))

Вуаля! У нас есть наш градиент. Однако мы пришли к нашему решению со скалярными правилами, просто сгруппировав числа в вектор. Есть ли способ представить правило цепи с несколькими переменными для векторов?

Прямо сейчас наш градиент вычисляется с помощью:

Изображение 32: ГрадиентYзнак равное(г(Икс))

Обратите внимание, что первый член градиентов обоихf₁ (х)а такжеf₂ (х)включает частичноеg₁надИкси второй член градиентов обоихf₁ (х)а такжеf₂ (х)включает частичноеg₂надИкс Это как умножение матриц! Поэтому мы можем представить это как:

Изображение 33: Векторное представление градиентаYзнак равное(г(Икс))

Давайте проверим наше новое представление правила цепочки векторов:

Изображение 34: Правило векторной цепи

Мы получаем тот же ответ, что и скалярный подход! Если вместо одного параметраИксу нас есть векторный параметрИкснам просто нужно немного изменить наше правило, чтобы получить полное правило цепочки векторов:

Изображение 35: Правило векторной цепи

Другими словами:

Изображение 36: Правило векторной цепи

В нашем примере выше,еэто чисто функцияг; то есть,фиявляется функциейсолдатно нетGJ(каждая функцияесоответствует ровно 1 функцииг),В этом случае все вне диагонали становится равным нулю, и:

Изображение 37: Особый случай векторного правила цепочки

Теперь у нас есть все части, которые мы находим в градиенте нейронной сети, с которой мы начали нашу серию:

Изображение 38: Функция стоимости

Проверять, выписыватьсяЧасть 4чтобы узнать, как вычислить его производную!

Если вы еще этого не сделали, прочитайте части 1 и 2:

ЧитатьЧасть 4для грандиозного финала!

Скачать оригинал статьиВот,

Если вам понравилась эта статья, не забудьте оставить несколько хлопков! Оставьте комментарий ниже, если у вас есть какие-либо вопросы или предложения 🙂

Оригинальная статья

Найти градиент функции в точке (1

Найти градиент функции в точке (1, 3)

Решение. Общее выражение для градиента есть

Подставив х=1, у=3, получаем:

Таким образом,

Вычислить производную функции по направлению вектора {3,4} в точке (1, 1)

Решение. Найдем градиент функции f

Таким образом, компоненты градиента f в точке М(1, 1)

. В векторном представлении

Направляющие косинусы: ,

Значит

Найти вторые производные функции

Решение. Находим первые производные:

Тогда вторые производные

Для поверхности, задаваемой уравнением написать уравнение касательной и нормали в точке (1, 1)

Решение. Уравнение касательной плоскости к поверхности, заданной уравнением F(x,y,z), в точке M₀(x₀, y₀, z₀) записывается в виде:

Теперь найдем частные производные (при этом, в первых двух случаях используем правило дифференцирования сложной функции одной переменной):

, . В точке (1, 1, 0) эти значения имеют вид {1, 3}.

Подставим полученные значения в уравнение касательной плоскости:

, получим касательную плоскость x+3y-4=0

Как известно, уравнение нормали к поверхности, заданной уравнением F(x,y,z), в точке M₀(x₀, y₀, z₀) записывается в виде:

или в нашем случае

Поскольку нормаль к поверхности есть (по определению) прямая линия, а в каноническом уравнении прямой числа, стоящие в знаменателях дробей, суть – координаты направляющего вектора этой прямой, то равенство нулю знаменателя третьей дроби, означает, что данная прямая лежит в плоскости, перпендикулярной оси OZ, и третьи координаты всех точек этой прямой совпадают между собой и равны третьей координате точки (1, 1, 0), так как по условию через нее проходит нормаль к поверхности.

Возьмём интеграл

Сделаем такую замену: ,

Тогда получим

Найти градиент, дивергенцию, ротор | Решатели

В области \(V\) задано скалярное поле, если каждой точке \(M\) из \(V\) поставлено в соответствие число \(u\left(M \right)\). Скалярное поле \(u\left(M \right)\) называется дифференцируемым в точке \(M_{0}\) из области \(V\), если приращение поля \(\Delta u\) в этой точке можно представить в виде: \(\Delta u=g\cdot \Delta r+o\left(\rho \right)\), где \(\rho =\rho \left(M_{0},M \right)\) — расстояние между точками \(M_{0}\) и \(M\), \(\Delta u=u\left(M \right)-u\left(M_{0} \right)\). Вектор \(g\left(M_{0} \right)\) называется градиентом дифференцируемого в точке \(M_{0}\) скалярного поля. В декартовой системе координат \[grad u=\frac{\partial u}{\partial x}i+\frac{\partial u}{\partial y}j+\frac{\partial u}{\partial z}k\] Если каждой точке \(M\) из области \(V\) поставлен в соответствие некоторый вектор \(F\left(M \right)\), то говорят, что в \(V\) задано векторное поле. Дивергенция — это линейный дифференциальный оператор на векторном поле, характеризующий поток данного поля через поверхность достаточно малой окрестности каждой внутренней точки области определения поля. Оператор дивергенции, примененный к полю \(F\), обозначается \(divF\) или \(\bigtriangledown \cdot F\).2
laplacian calculator
Вычислить выражения
div (grad f)
curl (curl F)
grad (F . G)
иллюстрация свойств градиента и пример с решением
Наибольший интерес представляет вопрос о направлении быстрейшего возрастания функции в точке . Вопрос просто решается с помощью вектора -градиента функции .
Градиентом функции в данной точке называется вектор, расположенный в плоскости с началом в точке
Основное свойство градиента: направление градиента функции в точке является направлением быстрейшего возрастания функции, его модуль равен наибольшей скорости возрастания в заданной точке.
Другое свойство градиента: он перпендикулярен касательной линии уровня, проходящей через точку начала градиента.
Иллюстрация свойств градиента — на рисунке 8.2. Показаны линии уровня , причем .
Через точку , лежащую на линии с уровнем проведены касательная и градиент, которые перпендикулярны друг другу. Градиент направлен в сторону возрастания функции .
8.6 Экстремум функции двух переменных. Необходимые и достаточные условия экстремума
Точка называется точкой максимума функции , если значение функции в этой точке больше, чем её значение в любой другой точке некоторой (хотя бы малой) окрестности точки . Аналогично (с заменой «больше» на «меньше») определяется точка минимума функции.
Точки минимума и максимума объединяются под общим названием точки экстремума.
Для функции двух переменных точка имеет две координаты для функции трёх переменных — три координаты . При этом окрестностью точки является открытый шар с центром в этой точке.
Поиск критических точек, т.е. точек в которых может быть экстремум функции , производится при помощи необходимого условия экстремума:
Решение системы (8.12) определяет координаты критических точек
Однако необходимого условия мало для существования точек экстремума.
Нужно провести исследование критических точек с использованием достаточных условий экстремума.
Для функции двух переменных введём обозначения для вторых частных производных в критической точке :
Достаточные условия приводим в таблице 4.
Таблица 4 — Достаточные условия экстремума функции двух переменных
Пример:
Дана функция и точка . Найти градиент функции в заданной точке .
Решение:
Используем формулу градиента
Определяем частные производные и вычисляем их при .
При вычислении частной производной по одной из переменных вторая переменная считается постоянной величиной.
Значения частных производных подставляем в формулу градиента:
Ответ: .
Эта лекция взята с этой страницы, там вы найдёте все темы лекций по высшей математике для студентов 1 курса:
Высшая математика для 1 курса
Возможно вам будут полезны эти страницы:
ГРАДИЕНТ ФУНКЦИИ — это… Что такое ГРАДИЕНТ ФУНКЦИИ?
ГРАДИЕНТ ФУНКЦИИ
и = f(x, у, z), заданной в некоторой обл. пространства (X Y Z), есть вектор с проекциями обозначаемый символами: grad где i, j, k — координатные орты. Г. ф. — есть функция точки (х, у, z), т. е. он образует векторное поле. Производная в направлении Г. ф. в данной точке достигает наибольшего значения и равна: Направление градиента есть направление наибыстрейшего возрастания функции. Г. ф. в данной точке перпендикулярен поверхности уровня, проходящей через эту точку. Эффективность использования Г. ф. при литологических исследованиях была показана при изучении эоловых отл. Центральных Каракумов.
Геологический словарь: в 2-х томах. — М.: Недра. Под редакцией К. Н. Паффенгольца и др.. 1978.
ГРАДИЕНТ ТЕКТОНИЧЕСКИХ ДВИЖЕНИЙ
ГРАДИЕНТ
Полезное

Смотреть что такое «ГРАДИЕНТ ФУНКЦИИ» в других словарях:
Градиент — Эта статья о математической характеристике; о способе заливки см.: Градиент (компьютерная графика) … Википедия
ГРАДИЕНТ — (лат.). Разность в барометрических и термометрических показаниях в разных местностях. Словарь иностранных слов, вошедших в состав русского языка. Чудинов А.Н., 1910. ГРАДИЕНТ разность в показаниях барометра и термометра в один и тот же момент… … Словарь иностранных слов русского языка
градиент — Изменение значения некоторой величины на единицу расстояния в заданном направлении. Топографический градиент — это изменение высоты местности на измеренном по горизонтали расстоянии. [http://www.oceanographers.ru/index.php?option=com… … Справочник технического переводчика
Градиент (в биологии) — Градиент в биологии, закономерное количественное изменение морфологических или функциональных, в том числе и биохимических, свойств вдоль одной из осей тела организма (или органа) на любой стадии его развития. Примеры Г.: убывание содержания… … Большая советская энциклопедия
градиент характеристики срабатывания функции дифференциальной защиты — [Интент] Тематики релейная защита EN gradient of the differential protection tripping characteristic … Справочник технического переводчика
Градиент — [gradient] вектор, направленный в сторону наискорейшего возрастания функции и равный по величине ее производной в этом направлении: где символами ei обозначены единичные векторы осей координат (орты) … Экономико-математический словарь
ГРАДИЕНТ — одно из основных понятий векторного анализа и теории нелинейных отображений. Градиентом скалярной функции векторного аргумента из евклидова пространства Е n наз. производная функции f(t).по векторному аргументу t, то есть n мерный вектор с… … Математическая энциклопедия
Градиент физиологический — – величина, отражающая изменение к либо показателя функции в зависимости от другой величины; напр., градиент парциального давления разность парциальных дав лений, определяющая диффузию газов из альвеол (акцинусов) в кровь и из крови в… … Словарь терминов по физиологии сельскохозяйственных животных
Градиент — I Градиент (от лат. gradiens, род. падеж gradientis шагающий) Вектор, показывающий направление наискорейшего изменения некоторой величины, значение которой меняется от одной точки пространства к другой (см. Поля теория). Если величина… … Большая советская энциклопедия
Градиент — (от лат. gradiens шагающий, идущий) (в математике) вектор, показывающий направление наискорейшего возрастания некоторой функции; (в физике) мера возрастания или убывания в пространстве или на плоскости какой либо физической величины на единицу… … Начала современного естествознания
Книги
Методы решения некоторых задач избранных разделов высшей математики. Практикум, Клименко Константин Григорьевич, Левицкая Галина Васильевна, Козловский Евгений Александрович. В данном практикуме рассматриваются методы решения некоторых типов задач из таких разделов общепринятого курса математического анализа, как предел и экстремум функции, градиент и производная… Подробнее Купить за 324 грн (только Украина)
Методы решения некоторых задач избранных разделов высшей математики. Практикум, Клименко Константин Григорьевич, Левицкая Галина Васильевна, Козловский Евгений Александрович. В данном практикуме рассматриваются методы решения некоторых типов задач из таких разделов общепринятого курса математического анализа, как предел и экстремум функции, градиент и производная… Подробнее Купить за 253 руб
Методы решения некоторых задач избранных разделов высшей математики. Практикум, Г. В. Левицкая. В данном практикуме рассматриваются методы решения некоторых типов задач из таких разделов общепринятого курса математического анализа, как предел и экстремум функции, градиент и производная… Подробнее Купить за 120 руб электронная книга

Градиент (уклон) прямой
Градиент (также называемый уклоном) прямой линии показывает, насколько крутой является прямая линия.
Рассчитать
Для расчета градиента:
Разделите изменение высоты на изменение горизонтального расстояния
Градиент = Изменение Y Изменение X
Поиграйте (перетащите точки):
Примеры:
Градиент = 3 3 = 1
Таким образом, градиент равен 1
Градиент = 4 2 = 2
Линия круче, поэтому Градиент больше.
Градиент = 3 5 = 0,6
Линия менее крутая, поэтому Градиент меньше.
Положительный или отрицательный?
Двигаясь слева направо, велосипедист должен пройти P на выезде P Угол наклона:
При измерении линии:
Начиная слева и переходя через вправо,
положительный (но переход влево отрицательный).
Вверх положительный , а вниз отрицательный
Градиент = −4 2 = −2
Эта линия идет на вниз на по мере вашего движения, поэтому градиент у нее отрицательный.
Прямо через

Градиент = 0 5 = 0
Линия, идущая прямо (по горизонтали), имеет нулевой градиент.
Прямо вверх и вниз
Градиент = 3 0 = undefined
Последний вариант немного сложен … вы не можете разделить на ноль,
, поэтому градиент «прямой вверх и вниз» (вертикальной) линии «неопределен».
Взлетай и беги
Иногда горизонтальное изменение называется «бегом», а вертикальное изменение — «подъемом» или «падением»:
Это просто разные слова, никакие вычисления не меняются.
Калькулятор уклона
По определению, наклон или уклон линии описывает ее крутизну, уклон или уклон.
Где
м — уклон
θ — угол наклона
Если известны 2 точки

Если известны 1 точка и наклон
Уклон, иногда называемый в математике градиентом, — это число, которое измеряет крутизну и направление линии или участка линии, соединяющей две точки, и обычно обозначается м .Как правило, крутизна линии измеряется абсолютным значением ее уклона, м . Чем больше значение, тем круче линия. Учитывая м , можно определить направление линии, которую описывает м , по ее знаку и значению:
Линия увеличивается и идет вверх слева направо, когда m> 0
Линия убывает и идет вниз слева направо, когда m <0
Линия имеет постоянный наклон и является горизонтальной при m = 0
Вертикальная линия имеет неопределенный наклон, так как это приведет к дроби с 0 в знаменателе.См. Приведенное ниже уравнение.
Наклон — это, по сути, изменение высоты при изменении расстояния по горизонтали, и его часто называют «подъем через пробег». Он находит применение в градиентах в географии, а также в гражданском строительстве, например, в строительстве дорог. В случае дороги «подъем» — это изменение высоты, а «пробег» — это разница в расстоянии между двумя фиксированными точками, если расстояние для измерения недостаточно велико, чтобы кривизна земли была рассматривается как фактор.Математически наклон представлен как:
В приведенном выше уравнении y ₂ — y ₁ = Δy или вертикальное изменение, а x ₂ — x ₁ = Δx или горизонтальное изменение, как показано на представленном графике. Также видно, что Δx и Δy — это отрезки прямых, которые образуют прямоугольный треугольник с гипотенузой d , причем d — это расстояние между точками (x ₁, y ₁) и (x ₂, y ₂) .Поскольку Δx и Δy образуют прямоугольный треугольник, можно вычислить d , используя теорему Пифагора. Обратитесь к калькулятору треугольника для получения более подробной информации о теореме Пифагора, а также о том, как рассчитать угол наклона θ , указанный в калькуляторе выше. Кратко:
d = √ (x ₂ — x ₁) ² + (y ₂ — y ₁) ²
Приведенное выше уравнение является теоремой Пифагора в своем корне, где гипотенуза d уже решена, а две другие стороны треугольника определяются вычитанием двух значений x и y , заданных двумя точками. .Учитывая две точки, можно найти θ , используя следующее уравнение:
m = тангенс угла (θ)
По точкам (3,4) и (6,8) найдите наклон прямой, расстояние между двумя точками и угол наклона:
d = √ (6-3) ² + (8-4) ² = 5
Хотя это выходит за рамки данного калькулятора, помимо его основного линейного использования, концепция наклона важна в дифференциальном исчислении. Для нелинейных функций скорость изменения кривой меняется, а производная функции в данной точке — это скорость изменения функции, представленная наклоном линии, касательной к кривой в этой точке.
8.3 Градиент линии | Аналитическая геометрия
Вам дана следующая диаграмма:
Вычислите уравнение прямой \ (AB \).
Чтобы вычислить уравнение прямой, мы сначала вычисляем градиент (\ (m \)) прямой \ (AB \):
\ (\ begin {выровнено} m & = \ frac {y_B — y_A} {x_B — x_A} \\ m & = \ frac {(- \ text {3,5}) — (\ text {2,5})} {(\ text {2}) — (- \ text {1})} \\ м & = — \ текст {2} \\ \ конец {выровнено} \)
Во-вторых, мы вычисляем значение \ (y \) — точки пересечения (\ (c \)) прямой \ (AB \).Мы делаем это подставив либо точку \ (A \), либо \ (B \) в общий вид прямой. Мы будем использовать точку \ (А \).
\ (\ begin {выровнено} у & = мх + с \\ (\ text {2,5}) & = (- \ text {2}) \ times (- \ text {1}) + c \\ c & = \ текст {0,5} \\ \ конец {выровнено} \)
Следовательно, уравнение прямой \ (AB \) выглядит следующим образом:
\ (\ begin {выровнено} у & = — \ текст {2} х + \ текст {0,5} \ конец {выровнено} \)
Вам дана следующая диаграмма:
Вычислите уравнение прямой \ (AB \).
Чтобы вычислить уравнение прямой, мы сначала вычисляем градиент (\ (m \)) прямой \ (AB \):
\ (\ begin {выровнено} m & = \ frac {y_B — y_A} {x_B — x_A} \\ m & = \ frac {(\ text {1,5}) — (- \ text {1})} {(\ text {4}) — (- \ text {1})} \\ м & = \ текст {0,5} \\ \ конец {выровнено} \)
Во-вторых, мы вычисляем значение \ (y \) — точки пересечения (\ (c \)) прямой \ (AB \).Мы делаем это подставив либо точку \ (A \), либо \ (B \) в общий вид прямой. Мы будем использовать точку \ (А \).
\ (\ begin {выровнено} у & = мх + с \\ (- \ text {1}) & = (\ text {0,5}) \ times (- \ text {1}) + c \\ c & = — \ text {0,5} \\ \ конец {выровнено} \)
Следовательно, уравнение прямой \ (AB \) выглядит следующим образом:
\ (\ begin {выровнено} y & = \ text {0,5} x — \ text {0,5} \ конец {выровнено} \)
Точки \ (P (-6; 2) \), \ (Q (2; -2) \) и \ (R (-3; r) \) лежат на прямой.Найдите значение \ (r \).
Поскольку три точки лежат на прямой, мы можем использовать тот факт, что градиент \ (PQ \) равен к градиенту \ (QR \), чтобы найти \ (r \).
Градиент \ (PQ \) составляет:
\ begin {align *} m_ {PQ} & = \ frac {y_2 — y_1} {x_2 — x_1} \\ & = \ frac {-2 — 2} {2 — (-6)} \\ & = \ frac {-4} {8} \\ & = — \ frac {1} {2} \ end {выровнять *}
И градиент \ (QR \) с точки зрения \ (r \) составляет:
\ begin {align *} m_ {QR} & = \ frac {y_2 — y_1} {x_2 — x_1} \\ & = \ frac {r — (-2)} {- 3 — 2} \\ & = \ frac {r + 2} {- 5} \ end {выровнять *}
Теперь положим \ (m_ {PR} = m_ {QR} = — \ frac {1} {2} \) и решим для \ (r \):
\ begin {align *} — \ frac {1} {2} & = \ frac {r + 2} {- 5} \\ (-1) \ раз (-5) & = 2 (г + 2) \\ 5 & = 2р + 4 \\ 5 — 4 & = 2р \\ 1 & = 2р \\ г & = \ гидроразрыв {1} {2} \ end {выровнять *}
Линия \ (PQ \) с \ (P (-1; -7) \) и \ (Q (q; 0) \) имеет градиент \ (\ text {1} \).Найдите \ (q \).
\ begin {align *} m_ {PQ} & = \ frac {y_2 — y_1} {x_2 — x_1} \\ 1 & = \ frac {0 — (-7)} {q — (-1)} \\ q + 1 & = 7 \\ q & = 6 \ end {выровнять *}
Вам дана следующая диаграмма:
Вам также сообщают, что линия \ (AB \) проходит параллельно следующей линии: \ (y = x — \ text {5} \).Точка \ (A \) находится в \ (\ left (-2; -4 \ right) \).
Найдите уравнение прямой \ (AB \).
Нам говорят, что прямая \ (AB \) параллельна \ (y = x — 5 \), поэтому градиент прямой \ (AB \) равен градиент \ (y = x — 5 \). Градиент \ (y = x — 5 \) равен 1.
Теперь мы можем использовать точку \ (A \) и градиент линии, чтобы найти точку пересечения линии \ (y \):
\ (\ begin {выровнено} у & = мх + с \\ (- \ text {4}) & = (\ text {1}) (- \ text {2}) + c \\ c & = — \ текст {2} \\ \ конец {выровнено} \)
Следовательно, уравнение прямой \ (AB \): \ (y = x — 2 \).
Вам дана следующая диаграмма:
Вам также сообщают, что линия \ (AB \) проходит параллельно следующей линии: \ (y = -x + \ text {4,5} \). Точка \ (A \) находится в \ (\ left (-1; \ text {2,5} \ right) \).
Найдите уравнение прямой \ (AB \).
Нам говорят, что линия \ (AB \) параллельна \ (y = -x + \ text {4,5} \), поэтому градиент линии \ (AB \) равен равен градиенту \ (y = -x + \ text {4,5} \).Градиент \ (y = -x + \ text {4,5} \) равен \(-\текст 1}\).
Теперь мы можем использовать точку \ (A \) и градиент линии, чтобы найти точку пересечения линии \ (y \):
\ (\ begin {выровнено} у & = мх + с \\ (\ text {2,5}) & = (- \ text {1}) \ times (- \ text {1}) + c \\ c & = \ текст {1,5} \\ \ конец {выровнено} \)
Следовательно, уравнение линии \ (AB \) будет: \ (y = -x + \ text {1,5} \).
Данная линия \ (AB \), которая проходит параллельно \ (y = \ text {0,5} x — \ text {6} \). Очки \ (A (-1; — \ text {2,5}) \) и \ (B (x; 0) \) также даны.
Вычислить недостающую координату точки \ (B \).
Нам говорят, что линия \ (AB \) параллельна \ (y = \ text {0,5} x — 6 \), поэтому градиент линии \ (AB \) равен равен градиенту \ (y = \ text {0,5} x — 6 \).Градиент \ (y = \ text {0,5} x — 6 \) равен \ (\ text {0,5} \).
Теперь мы можем использовать точку \ (A \) и градиент линии, чтобы найти точку пересечения линии \ (y \):
\ begin {align *} у & = мх + с \\ (- \ text {2,5}) & = (\ text {0,5}) (- \ text {1}) + c \\ c & = — \ текст {2} \\ \ end {выровнять *}
Следовательно, уравнение прямой \ (AB \) будет: \ (y = \ text {0,5} x — 2 \).
Теперь мы можем подставить точку \ (B \) в уравнение прямой \ (AB \), чтобы найти \ (x \):
\ begin {align *} у & = \ текст {0,5} х — 2 \\ 0 & = \ text {0,5} x — 2 \\ 4 & = х \ end {выровнять *}
Следовательно, координаты точки \ (B \) равны \ ((0; 4) \).
Данная линия \ (AB \), которая проходит параллельно \ (y = — \ text {1,5} x + \ text {4} \). Точки Также указаны \ (A (- \ text {2}; \ text {4}) \) и \ (B (2; y) \).
Вычислить недостающую координату точки \ (B (2; y) \).
Нам говорят, что линия \ (AB \) параллельна \ (y = — \ text {1,5} x + 4 \), поэтому градиент линии \ (AB \) равен равен градиенту \ (y = — \ text {1,5} x + 4 \).Градиент \ (y = — \ text {1,5} x + 4 \) равен \ (- \ text {1,5} \).
Теперь мы можем использовать точку \ (A \) и градиент линии, чтобы найти точку пересечения линии \ (y \):
\ begin {align *} у & = мх + с \\ (\ text {4}) & = (- \ text {1,5}) (- \ text {2}) + c \\ c & = \ текст {1} \\ \ end {выровнять *}
Следовательно, уравнение прямой \ (AB \) будет: \ (y = — \ text {1,5} x + 1 \).
Теперь мы можем подставить точку \ (B \) в уравнение прямой \ (AB \), чтобы найти \ (x \):
\ begin {align *} у & = — \ текст {1,5} х + 1 \\ y & = — \ text {1,5} (2) + 1 \\ y & = -2 \ end {выровнять *}
Следовательно, координаты точки \ (B \) равны \ ((2; -2) \).
На графике показана линия \ (AB \). Синяя пунктирная линия перпендикулярна \ (AB \).
Уравнение синей пунктирной линии: \ (y = x + 1 \). Точка \ (A \) находится в точке \ ((- 2; 4) \).
Определите уравнение прямой \ (AB \).
Общая форма прямой: \ (y = mx + c \).
Линия \ (AB \) перпендикулярна синей пунктирной линии, поэтому \ (m_ {AB} = \ dfrac {-1} {m _ {\ text {blue линия}}}\).
\ begin {align *} у & = мх + с \\ y & = \ left (\ frac {-1} {m _ {\ text {синяя линия}}} \ right) x + c \\ y & = \ left (\ frac {-1} {\ text {1}} \ right) x + c \\ у & = -x + c \ end {выровнять *}
Теперь мы можем подставить координаты точки \ (A \), чтобы найти точку пересечения \ (y \):
\ begin {align *} у & = мх + с \\ (\ text {4}) & = (- \ text {1}) (- \ text {2}) + c \\ c & = \ текст {2} \\ \ end {выровнять *}
Следовательно, уравнение прямой \ (AB \): \ (y = -x + 2 \).
На графике показана линия \ (AB \). Синяя пунктирная линия перпендикулярна \ (AB \).
Уравнение синей пунктирной линии: \ (y = — \ text {0,5} x — \ text {0,5} \). Точка \ (A \) находится в \ ((- \ text {1}; — \ text {3,5}) \).
Определите уравнение прямой \ (AB \).
Общая форма прямой: \ (y = mx + c \).
Линия \ (AB \) перпендикулярна синей пунктирной линии, поэтому \ (m_ {AB} = \ dfrac {-1} {m _ {\ text {blue линия}}}\).
\ begin {align *} у & = мх + с \\ y & = \ left (\ frac {-1} {m _ {\ text {синяя линия}}} \ right) x + c \\ y & = \ left (\ frac {-1} {- \ text {0,5}} \ right) x + c \\ у & = 2x + c \ end {выровнять *}
Теперь мы можем подставить координаты точки \ (A \), чтобы найти точку пересечения \ (y \):
\ begin {align *} у & = мх + с \\ (- \ text {3,5}) & = (\ text {2}) (- \ text {1}) + c \\ c & = — \ text {1,5} \\ \ end {выровнять *}
Следовательно, уравнение прямой \ (AB \) будет: \ (y = 2x — \ text {1,5} \).
Дана прямая \ (AB \), которая проходит перпендикулярно прямой \ (CD \) с уравнением \ (y = -2x + 1 \). Точки Также указаны \ (A (-5; -1) \) и \ (B (3; a) \).
Вычислить недостающую координату точки \ (B \).
Общая форма прямой: \ (y = mx + c \).
Линия \ (AB \) перпендикулярна линии \ (CD \), поэтому \ (m_ {AB} = \ dfrac {-1} {m_ {CD}} \).
\ begin {align *} у & = мх + с \\ y & = \ left (\ frac {-1} {m_ {CD}} \ right) x + c \\ y & = \ left (\ frac {-1} {- \ text {2}} \ right) x + c \\ у & = \ текст {0,5} х + с \ end {выровнять *}
Теперь мы можем подставить точку \ (A \) в уравнение, чтобы найти точку пересечения \ (y \):
\ begin {align *} у & = \ текст {0,5} х + с \\ — \ text {1} & = (\ text {0,5}) (- \ text {5}) + c \\ c & = \ текст {1,5} \ end {выровнять *}
Затем мы можем подставить в точку \ (B \), чтобы найти недостающую координату:
\ begin {align *} y & = \ text {0,5} x + \ text {1,5} \\ a & = (\ text {0,5}) (\ text {3}) + \ text {1,5} \\ & = \ текст {3} \ end {выровнять *}
Следовательно, отсутствует координата \ (B (3; 3) \).
Данная линия \ (AB \), которая проходит перпендикулярно линии \ (CD \) с уравнением \ (y = 2x — \ text {0,75} \). Также указаны точки \ (A (-5; 1) \) и \ (B (a; — \ text {2,5}) \).
Вычислить недостающую координату точки \ (B \).
Общая форма прямой: \ (y = mx + c \).
Линия \ (AB \) перпендикулярна линии \ (CD \), поэтому \ (m_ {AB} = \ dfrac {-1} {m_ {CD}} \).
\ begin {align *} у & = мх + с \\ y & = \ left (\ frac {-1} {m_ {CD}} \ right) x + c \\ y & = \ left (\ frac {-1} {2} \ right) x + c \\ у & = — \ текст {0,5} х + с \ end {выровнять *}
Теперь мы можем подставить точку \ (A \) в уравнение, чтобы найти точку пересечения \ (y \):
\ begin {align *} у & = — \ текст {0,5} х + с \\ \ text {1} & = (\ text {0,5}) (- \ text {5}) + c \\ c & = — \ text {1,5} \ end {выровнять *}
Затем мы можем подставить в точку \ (B \), чтобы найти недостающую координату:
\ begin {align *} y & = \ text {0,5} x — \ text {1,5} \\ — \ text {2,5} & = \ text {0,5} a — \ text {1,5} \\ а & = — \ текст {2} \ end {выровнять *}
Следовательно, отсутствует координата \ (B (-2; — \ text {2,5}) \).
Вам дана следующая диаграмма:
Вам также сообщают, что строка \ (AB \) имеет следующее уравнение: \ (y = — \ text {0,5} x + \ text {1,5} \).
Вычислить недостающую координату точки \ (B \).
Подставляем известное значение для точки \ (B \) в уравнение и решаем неизвестное значение:
\ (\ begin {выровнено} y & = (- \ text {0,5}) x + \ text {1,5} \\ a & = (- \ text {0,5}) (\ text {2}) + \ text {1,5} \\ & = \ текст {0,5} \ конец {выровнено} \)
Вам дана следующая диаграмма:
Вам также сообщают, что строка \ (AB \) имеет следующее уравнение: \ (y = \ text {0,5} x — \ text {1} \).
Вычислить недостающую координату точки \ (B \).
Подставляем известное значение для точки \ (B \) в уравнение и решаем неизвестное значение:
\ (\ begin {выровнено} y & = (\ text {0,5}) x — \ text {1} \\ a & = (\ text {0,5}) (\ text {1}) — \ text {1} \\ & = — \ текст {0,5} \ конец {выровнено} \)
\ (A \) — это точка \ ((- 3; -5) \), а \ (B \) — это точка \ ((n; -11) \).\ (AB \) перпендикулярно прямой \ (CD \) с уравнением \ (y = \ frac {3} {2} x — 5 \). Найдите значение \ (n \).
Линия \ (AB \) перпендикулярна линии \ (CD \), поэтому \ (m_ {AB} = \ dfrac {-1} {m_ {CD}} \).
\ begin {align *} m_ {AB} & = -1 \ div \ frac {3} {2} \\ & = \ frac {-2} {3} \ end {выровнять *}
Следовательно:
\ begin {align *} \ frac {-2} {3} & = \ frac {-11 — (-5)} {n — (-3)} \\ \ frac {-2} {3} & = \ frac {-6} {n + 3} \\ \ frac {-2} {3} (n + 3) & = -6 \\ -2 (п + 3) & = -18 \\ п + 3 & = 9 \\ n & = 6 \ end {выровнять *}
Даны баллы \ (A (4; -3) \), \ (B (-5; 0) \) и \ (C (-3; p) \).Определите значение \ (p \), если \ (A \), \ (B \) и \ (C \) коллинеарны.
Нам говорят, что \ (A \), \ (B \) и \ (C \) коллинеарны, поэтому \ (m_ {AB} = m_ {BC} \).
\ begin {align *} \ frac {0 + 3} {- 5 — 4} & = \ frac {p} {- 3 + 5} \\ \ frac {3} {- 9} & = \ frac {p} {2} \\ \ поэтому p & = \ frac {6} {- 9} \\ & = \ frac {-2} {3} \ end {выровнять *}
Как рассчитать уклон / уклон? «Подъем через бег» в геолого-геофизических исследованиях
Многие из нас знают, что наклон линии рассчитывается по методу «подъем за пробегом».Однако применение расчета уклона может показаться немного более сложным. В области наук о Земле вас могут попросить вычислить наклон холма или определить скорость, вычислив наклон линии на графике. Эта страница предназначена для того, чтобы помочь вам освоить эти навыки, чтобы вы могли использовать их в своих курсах геолого-геофизических исследований.
Почему я должен рассчитывать уклон или уклон?
В науках о Земле склон может сыграть важную роль в решении ряда задач. Наклон холма может помочь определить степень вероятной эрозии во время ливня.Градиент уровня грунтовых вод может помочь нам понять, может ли (и насколько) загрязнение повлиять на местный колодец или источник воды.
Как рассчитать уклон (или уклон) в науках о Земле?
Градиент в случае склона холма и уровня грунтовых вод аналогичен вычислению наклона линии на графике — «подъем» над «бегом». Но как это сделать с помощью контурной (или топографической) карты?
Сначала ознакомьтесь с особенностями интересующей топографической карты.Убедитесь, что вы знаете несколько вещей:
Что такое интервал между контурами (иногда сокращенно CI)?
Каков масштаб карты?
Для какого объекта вы хотите узнать наклон?
Ниже представлена топографическая карта Math State Park. Вам интересно построить путь от вершины холма на этой карте к ручью (Equation Creek) и вы хотите узнать наклон холма. Вам, вероятно, следует распечатать карту (с инструкциями по вычислению уклона) (Acrobat (PDF) 93kB Oct15 08)..
Каков интервал изолиний на этой карте?
Интервал изолиний сообщает вам «подъем», в частности, изменение высоты между каждой из «коричневых линий» (контуров). В этом случае интервал между контурами указывается клавишей в правом нижнем углу и обозначается сокращенно CI. Интервал изолиний 20 футов.
Каков масштаб карты?
Шкала показывает «пробег» или расстояние до земли.На этой карте он также показан в правом нижнем углу и отображается только графически. Если вы распечатаете карту (с инструкциями по вычислению уклона) (Acrobat (PDF) 93 КБ, 15 октября 2008 г.), вы обнаружите, что 1 дюйм = 1 миля.
Для какого объекта вы хотите узнать наклон?
В этом случае вам нужно знать наклон склона к ЗСЗ от вершины (на высоте 869 футов) до ручья.
Во-первых, вам нужно знать «подъем» для функции.«Подъем» — это разница в высоте сверху вниз (см. Изображение выше). Так определите высоту вершины холма (или склона, или уровня грунтовых вод).
Вершина интересующего нас холма составляет 859 футов. Линия контура у ручья, где закончится ваш путь, ниже 700 футов. Это составляет 680 футов (поскольку интервал изолиний составляет 20 футов). Перепад высот равен верху минус низу (859 футов — 680 футов), поэтому «подъем» = 179 футов
Затем вам нужно знать, «запустить» для этой функции.«Бег» — это расстояние по горизонтали от самой высокой отметки до самой низкой. Итак, возьмите линейку и измерьте это расстояние. Если вы знаете масштаб, вы можете рассчитать расстояние. В большинстве случаев расстояние на картах указывается в километрах или милях.
Красная линия обозначает расстояние вдоль склона холма, на котором вы хотите проложить свой путь. Красная линия вдвое длиннее шкалы одной мили (на распечатанной карте это около 2 дюймов). Таким образом, расстояние от вершины до низа холма или «пробега» = 2 мили
Теперь идет часть подъема по пробегу.Есть два способа, которыми вас могут попросить произвести расчеты, связанные с уклоном. Убедитесь, что вы знаете, о чем вас спрашивает, и выполните шаги, связанные с соответствующим процессом:
Если вас попросят рассчитать уклон (как на линии или на склоне холма), все, что вам нужно, — это простое деление. Просто убедитесь, что вы отслеживаете единицы!
Как мы видели на этой странице, уклон — это «подъем за шагом». Фраза «подъем через бег» подразумевает, что вам нужно будет разделить.Уравнение для наклона выглядит так:
Возьмите разницу в высоте и разделите ее на разницу по горизонтали (всегда следите за единицами измерения). На карте государственного парка Математика высота холма составляет 179 футов, а расстояние до него составляет 2 мили. Итак, мы ставим задачу так:
Завершите расчет с помощью калькулятора (или произведите вычисления вручную). Теперь просто разделим подъем на разбег и завершим:
Единицами измерения, которые вы получите, могут быть футы / мили, м / км или футы / фут (наклон можно выразить всеми этими способами).Это просто зависит от того, с чего вы начали.
Вас также могут попросить вычислить процент (или%) наклона . Этот расчет занимает пару шагов. И в основном это связано с уделением внимания юнитам. Единицы подъема и бега должны быть одинаковыми.
Чтобы вычислить процент уклона , подъем и спуск должны быть в одних и тех же единицах (например, в футах или метрах).Если расстояние по горизонтали выражено в милях, необходимо преобразовать в футы; если расстояние по горизонтали выражено в километрах, вам придется преобразовать в метры. (Чтобы преобразовать мили в футы, умножьте на 5280 фут / миль; км в м, умножьте на 1000 м / км. Если вам нужна дополнительная помощь или необходимо преобразовать другие единицы, см. Модуль преобразования единиц). Прямо сейчас вы встаете на ноги и пробегаете мили. Давайте переведем мили в футы, умножив на соответствующий коэффициент преобразования: 1 миля = 5280 футов.Итак, мы должны умножить «бег» на:
После преобразования, так что и высота, и расстояние имеют одни и те же единицы, мы можем написать уравнение для уклона: подъем за пробегом (подразумевая подъем, деленный на пробег). Мы знаем, что подъем составляет 179 футов, а бег — 10560 футов:
Но подождите, есть еще один шаг к достижению% наклона.
Чтобы получить%, нам нужно умножить вычисленный наклон (безразмерный, потому что единицы взаимно компенсируются сверху и снизу) на 100, чтобы наше уравнение выглядело следующим образом: Начните с подъема через бег и умножьте на 100:
Теперь введите свои числа и вычислите% крутизны! Обратите внимание, что% slope не имеет единиц измерения, потому что ft отменяет при вычислении.Убедитесь, что вы указали, что это%, однако!
Следующие шаги
ГОТОВ к практике (на эти проблемы проработаны ответы)
Градиент (или наклон) линии и наклон

Приложение: Дорожный знак, обозначающий крутой уклон.
Уклон дороги «15%» эквивалентен «m = 0,15».
Уклон (также известный как уклон ) линии определяется как
`» gradient «= текст (вертикальный подъем) / текст (горизонтальный бег`
На следующей диаграмме уклон линии AB определяется как: `a / b`
Как правило, для линии, соединяющей точки ( x ₁, y ₁) и ( x ₂, у ₂) имеем:
Теперь мы можем написать формулу для наклона прямой.
Градиент линии формулы
Как видно из диаграммы выше, уклон (обычно обозначается м ) определяется как:
`m = (y_2-y_1) / (x_2-x_1`
Интерактивный график — наклон линии
Вы можете изучить концепцию наклона линии на следующем интерактивном графике (это не фиксированное изображение).
Перетащите либо точку A ( x ₁, y ₁) или точку B ( x ₂, y ₂ градиент), чтобы исследовать, как работает.Числа будут обновляться по мере взаимодействия с графиком.
Обратите внимание, что происходит со знаком (плюс или минус) наклона, когда точка B находится выше или ниже A.
Наклон `= (y_2 — y_1) / (x_2 — x_1)`
`= (BC) / (AC)`
Авторские права © www.intmath.com
Вы можете перемещать график вверх-вниз, влево-вправо, если удерживаете клавишу «Shift», а затем перетаскиваете график.
Если заблудились, всегда можно обновить страницу.
Пример
Найдите наклон прямой, соединяющей точки (−4, −1) и (2, −5).
Ответ
Это задействованные точки:
Итак, уклон:
`m = (y_2-y_1) / (x_2-x_1`
`= (- 5 — (- 1)) / (2 — (- 4)`
`= (- 4) / 6`
`= -2 / 3`
Обратите внимание, что наклон отрицательный . Линия идет «вниз по склону», когда мы движемся слева направо.
Положительные и отрицательные наклоны
Как правило, положительный наклон указывает значение зависимой переменной (обычно y ) увеличивается при движении слева направо:
Зависимая переменная на приведенном выше графике — это значение y , а независимая переменная — x .
Отрицательный наклон означает, что значение зависимой переменной (обычно y ) равно , уменьшаясь на , когда мы идем слева направо:
Наклон
У нас есть линия с уклоном м и углом, который эта линия образует с x — ось α.
Из тригонометрии напомним, что тангенс угла α определяется как:
`tan \ alpha = текст (напротив) / текст (рядом)`
Теперь, поскольку наклон также определяется как противоположный / смежный, мы имеем:
Это дает нам результат:
тангенс угла α = м
Тогда мы можем найти угол α , используя
α = arctan м
(то есть α = tan ^-1 м )
Этот угол α называется углом наклона линии .@ `
ПРИМЕЧАНИЕ: Размер угла α (по определению) только между `0 °` и `180 °`.
Упражнение 2
Найдите наклон прямой α = 137 °.
Ответ
Ситуация следующая:
Итак, уклон:
м = tan α
= загар 137 °
= -0,933
Обратите внимание, что наклон отрицательный.
Как найти уклон в Google Таблицах

Пользователям электронных таблиц часто требуется вычислить наклон линии, связанной с данными в их электронной таблице. Если вы новый пользователь или привыкли использовать Microsoft Excel, может быть немного сложно понять, как это сделать самостоятельно.
Из этой статьи вы научитесь рассчитывать значения уклона в Google Таблицах с графиками и без них.
Что такое уклон?
Прежде всего, что такое наклон в Google Таблицах?
Наклон — это геометрическое понятие, которое описывает направление и крутизну линии на декартовой плоскости.(Декартова плоскость — это стандартная сетка x-y, которую вы, возможно, помните по математическим классам с осью X и осью Y.)
Линия, которая идет вверх слева направо на плоскости, имеет положительный наклон; линия, идущая вниз слева направо, имеет отрицательный наклон.
На диаграмме ниже синяя линия имеет положительный наклон, а красная линия имеет отрицательный наклон:
Наклон выражается числом, и это число указывает, насколько линия поднимается или опускается на заданном расстоянии.Если линия идет от X = 1, Y = 0 до X = 2, Y = 1 (то есть линия идет вверх на +1 по оси Y, а также на +1 по оси X), наклон равно 1. Если бы он увеличился с X = 1, Y = 0 до X = 2, Y = 2, наклон был бы равен 2 и так далее.
Чем больше число, тем круче наклон; наклон +10 означает линию, которая идет вверх на 10 по оси Y для каждой единицы, которую она перемещает по оси X, а наклон -10 означает линию, которая идет вниз на 10 по оси Y для каждой единицы на ось X.
В электронной таблице значения наклона обычно связаны с линейной регрессией, которая является способом анализа взаимосвязи между двумя или более переменными.
Переменные состоят из зависимых значений Y и независимых X, которые в электронных таблицах будут храниться в виде двух отдельных столбцов таблицы.
Зависимое значение — это значение, которое автоматически изменяется в результате подсчета, а независимое значение — это значение, которое может изменяться свободно. Типичным примером может быть один столбец (зависимая переменная X), который содержит ряд дат, с другим столбцом (независимая переменная Y), который содержит числовые данные, например, цифры продаж за этот месяц.
Где линии? Где график? Наклон — это то, как движется линия, верно?
Думайте о данных электронной таблицы как о точках графика. Данные, представленные в этой таблице, можно легко визуализировать с помощью линейного графика.
Как найти уклон в Google Таблицах
Google Таблицы предоставляет простой, но мощный набор инструментов для создания линейных графиков из табличных данных. В этом примере все, что вам нужно сделать, это выбрать всю таблицу данных (от A1 до B16) и нажать кнопку «Вставить диаграмму».После этого в Таблицах мгновенно появится следующая диаграмма:
Щелкните значок диаграммы. В одних местах он снижается, в других — растет! Как вы можете представить себе наклон такой безумной линии? Ответ — так называемая линия тренда. Линия тренда — это сглаженная версия вашей линии, которая показывает общую тенденцию в цифрах.
Щелкните Редактировать диаграмму . Получить линию тренда в Таблицах также просто.
Щелкните линию тренда.В открывшемся редакторе диаграмм щелкните вкладку «Настройка» и измените тип диаграммы на Точечная диаграмма .
Щелкните вкладку Customize , откройте раскрывающийся раздел Series и переключите Trendline.
Теперь ваш график должен выглядеть так:
Голубая линия, следующая за цепочкой точек на графике, является линией тренда.
Итак, как найти наклон этой линии?
Что ж, если бы это был урок математики, вам пришлось бы заняться математикой.К счастью, сейчас 21 век, и математика уже позади. Вместо этого мы можем просто сказать компьютеру сделать это за нас. Спасибо, Google.
Как найти наклон графика в Google Таблицах
В редакторе диаграмм мы можем использовать Google Таблицы для вычисления наклона. Просто следуйте этим инструкциям, чтобы найти наклон любого линейного графика в Google Таблицах.
Выберите Label > Используйте уравнение . Это добавит уравнение, которое Google Таблицы использовали для вычисления линии тренда, а наклон нашей линии будет частью слева от члена * x .
В данном случае наклон равен +1251. Это означает, что за каждый прошедший месяц выручка от продаж будет увеличиваться в общей сложности на 1251 доллар.
3. Интересно, что вам вовсе не обязательно иметь диаграмму, чтобы вычислить наклон. В Google Таблицах есть функция НАКЛОН , которая вычисляет наклон любой таблицы данных, не утруждая себя рисованием сначала в виде изображения. (Однако рисование картинок очень помогает узнать, как все это делать, поэтому мы с самого начала сделали это именно так.)
4. Вместо создания диаграммы вы можете просто добавить функцию НАКЛОН в ячейку вашей электронной таблицы. Синтаксис функции SLOPE в Google Таблицах: SLOPE (data_y, data_x) . Эта функция вернет то же значение наклона, что и в уравнении графика.
Обратите внимание, что порядок ввода немного отличается от того, как вы, вероятно, отображаете информацию в своей таблице. Это связано с тем, что Sheets хочет, чтобы вы сначала поместили независимые данные (доход от продаж), а затем зависимую переменную (месяц).
Также следует отметить, что функция SLOPE не так умна, как создание диаграммы. Для зависимой переменной требуются чистые числовые данные, поэтому я изменил эти ячейки на значения от 1 до 15.
Выберите любую пустую ячейку в электронной таблице и введите « = НАКЛОН (b2: b16, a2: a16) » и ударил Возврат .
И вот наш угол наклона с немного большей точностью, чем тот, который представлен на диаграмме.
Последние мысли
Вот как вы можете найти наклон в Google Таблицах.Надеюсь, что если у вас возникли проблемы с выяснением этого самостоятельно, эти инструкции могут вам помочь.
Если вы предпочитаете использовать Excel вместо Таблиц, есть также руководство TechJunkie по поиску значений уклона в Excel.
У вас есть интересные приложения для поиска наклона в Google Таблицах? Поделитесь ими с нами ниже!
ГРАДИЕНТ
ГРАДИЕНТ
КОНЦЕПЦИЯ ГРАДИЕНТА
«Не то чтобы я ленивый, но прежде, чем я отправлюсь в экспедицию, я хотел бы знать, сколько в нем тупиков и тупиков!»
«Что вам нужно знать, Лу, это градиент! Градиент говорит вам, насколько крутой ваш маршрут! Градиент можно выразить численно разными способами.Один из распространенных способов описания средней крутизны или уклона между двумя точками — это указать разницу в высоте (ED), деленную на горизонтальное расстояние (HD): ГРАДИЕНТ = ED / HD
Взгляните на этот пример:
Расстояние по вертикали (здесь разница высот между точками A и B) = 10 000 футов.
Горизонтальное расстояние от A до B = 5 миль.
Градиент = расстояние по вертикали (перепад высот (ED)), деленное на расстояние по горизонтали (HD)
Градиент составляет 2000 футов на милю (10000 футов, разделенных на 5 миль)
Перепад высот также может быть выражен в дюймах, метрах или в других удобных единицах измерения; аналогично горизонтальное расстояние может быть выражено в футах, километрах и т. д.Таким образом, уклон может быть указан как дюйм / фут, фут / миля, метр / километр и т. Д.
На диаграмме справа показаны некоторые уклоны и их приблизительные уклоны в футах / милях.
«Давайте посмотрим на пример рядом с домом: вход в Бойлан Холл в Бруклинском колледже. Есть два способа подняться на уровень дверей из четырехугольника:
Используя шаги.
Использование пандуса.
Как вы думаете, что круче? »
« Ну конечно ступеньки круче пандуса! Вы идете вверх на на ту же сумму, но на более короткое расстояние! Но хотелось бы знать, насколько намного круче !! «
» Вот где градиент может вам помочь! Давайте подробнее рассмотрим, что это такое! Вот фото ступеней: «
» А вот и эскиз ступеней!
Если вы присмотритесь, то увидите, что для того, чтобы попасть с земли на уровень дверей в здание (платформа 2), вам нужно подняться по девяти «подступенкам» и по семи ступеням и по платформе 1! Верно? »
« А теперь предположим, Лу, что я говорю вам, что подступенки — 6 дюймов в высоту, ступени — 12 дюймов в поперечнике, а Платформа 1 — 6 футов в ширину! А теперь скажите мне следующее: «
ИНСТРУКЦИИ: Заполните каждое поле и нажмите кнопку справа, чтобы проверить правильность вашего ответа. ИСПОЛЬЗУЙТЕ ТОЛЬКО ЦИФРЫ, А НЕ БУКВЫ!
1. Двигаясь от места, где земля встречается с первым подступенком, до места, где платформа 2 встречается со ступенями
общее расстояние по вертикали: — дюймы. Верный?:-
2. Двигаясь от места, где земля встречается с первым подступенком, до места, где платформа 2 встречается со ступенями
общее горизонтальное расстояние составляет: — ноги. Верный?:-
«После того, как вы ответили правильно, у вас есть мера общей крутизны! То есть вы в среднем получили крутизны двух наборов ступеней и платформы 1!
На эскизе вы можете видеть, что крутизна ступеней (розовый) и горизонтальность платформы 1 (зеленый), усредненные вместе, дают общую крутизну (красный).«
» И если я хочу присвоить общей крутизне число , все, что мне нужно сделать, это взять ответ на первый вопрос (общее вертикальное расстояние) и сравнить его. к ответу на второй вопрос (общее расстояние по горизонтали)! Я могу сказать, что чтобы перейти от земли к Платформе 2 (уровень двери), мне нужно подняться (а) ______ дюймов в (b) _______ футов в поперечнике! Более элегантно, я могу разделить расстояние по вертикали на расстояние по горизонтали, чтобы сказать, что в среднем я поднимаюсь (c) _____ дюймов на каждый фут в поперечнике! То есть градиент составляет (d) _______ дюймов на фут! »
Чтобы заполнить пустые поля, заполните форму ниже.
ИНСТРУКЦИИ: Заполните каждое поле и нажмите кнопку справа, чтобы проверить правильность вашего ответа. ИСПОЛЬЗУЙТЕ ТОЛЬКО ЦИФРЫ, А НЕ БУКВЫ!
Ответ на (а): — дюймы. Верный?:-
2. Ответ на (b): — ноги. Верный?:-
3. Ответ на (c) (с точностью до дюйма): — дюймы на каждый фут в поперечнике. Верный?:-
4.Ответ на (d) (с точностью до дюйма): — дюймов на фут. Верный?:-
«А теперь посмотрим на пандус!»
«На пути от уровня земли к платформе 2 пандус состоит из трех частей:
нижний пандус
поворотная платформа
верхний пандус
»
А теперь, Лу, выясни общую крутизну пандуса! Помните, что вертикальное расстояние будет таким же, как и для ступенек — вы снова переходите с уровня земли на платформу 2! Это расстояние по горизонтали, которое вы должны вычислить! Убедитесь, что вы включили все части маршрута (показаны фиолетовым цветом): горизонтальное расстояние для нижнего пандуса
три части поворота вокруг
горизонтальное расстояние для верхнего пандуса

ИНСТРУКЦИИ: Заполните каждое поле и нажмите кнопку справа, чтобы проверить правильность вашего ответа. ИСПОЛЬЗУЙТЕ ТОЛЬКО ЦИФРЫ, А НЕ БУКВЫ!
1. Общее вертикальное расстояние составляет: — дюймы. Верный?:-
2. Общее горизонтальное расстояние составляет: — ноги. Верный?:-
3. В среднем, количество дюймов, на которое поднимается пандус (с точностью до дюйма), составляет дюймы на каждый фут в поперечнике. Верный?:-
4. То есть средний градиент до ближайшего дюйма равен дюймов на фут.Верный?:-
ИЗМЕРЕНИЕ ГРАДИЕНТА НА КОНТУРНЫХ КАРТАХ
«Градиент можно рассчитать по контурным картам! Предположим, вы планируете« бушвак »по прямой от« A »до« B »и хотите узнать, насколько крутым он будет.« A »попадает на него. контур 2500 футов; B попадает на контур 1250 футов. Таким образом, перепад высот (расстояние по вертикали) составляет 1250 футов. Расстояние по горизонтали от A до B можно определить по шкале! Расстояние на карте от «A» до «B» составляет 1 дюйм! На земле это равно пяти милям! Итак, уклон составляет 1250 футов / 5 миль! Делитесь, и вы получаете 250 футов на милю! »
«И предположим, вы хотите проложить свой путь вверх по реке от точки« D »до« C »! Таким же образом можно получить уклон реки! Точка «C» находится на полпути между контурами 1750 ‘и 2000’, поэтому мы можем оценить ее высоту как середину между двумя контурами: 1875 ‘.Высота точки «D» равна 0, потому что она находится на уровне моря. Итак, разница высот между C и D составляет 1875 футов минус 0 = 1875 футов!
Горизонтальное расстояние вдоль реки примерно вдвое превышает длину масштабной линейки. Поскольку масштабная линейка составляет 5 миль, удвоенная ее длина составляет десять миль. Таким образом, уклон реки составляет 1875 футов / 10 миль = примерно 188 футов на милю! «
» Но расстояние между контурами и уклон меняются по мере продвижения река! »
« Ты прав, Лу! Полученный таким образом градиент — только СРЕДНИЙ ГРАДИЕНТ! Кроме того, невозможно узнать, какой градиент равен между контурами ! Интервал между контурами составляет 250 футов, так что может быть водопад в сто футов, а затем между двумя контурами будет достаточно ровный участок, и они не будут отображаться на карте! Но это дает вам общее представление о того, с чем вы столкнетесь! » отрезок бечевки вдоль линии.
Опубликовано в Разное
Навигация по записям
← Как сделать крутую фотку на аву: 9 советов для создания идеального снимка [2019]
Фотошоп платный: Приложение для обработки фотографий, редактирования изображений и дизайна →
Добавить комментарий Отменить ответ
Ваш адрес email не будет опубликован. Обязательные поля помечены *
Комментарий *
Имя *
Email *
Сайт

Искать:
Рубрики
Adobe CS3
Adobe CS4
Adobe CS5
Adobe CS6
Cs3
Cs4
Cs5
Cs6
Всё о дизайне
Для начинающих
Разное
Уроки для начинающих
Авторское право © 2024 Es picture - Картинки
top

		Градиент = 4 2 = 2
Линия круче, поэтому Градиент больше.

		Градиент = 3 5 = 0,6
Линия менее крутая, поэтому Градиент меньше.