3.1.3. Магниторезистивный эффект (эффект Гаусса)
Магниторезистивный эффект (эффект Гаусса) – изменение удельного сопротивления проводниковых и полупроводниковых материалов в магнитном поле.
На рис. 3.4 показана структурная схема эффекта. При помещении образца прямоугольного сечения из проводникового или полупроводникового материала в магнитное поле и при пропускании по нему электрического тока, направление которого перпендикулярно вектору индукции магнитного поля, сопротивление образца будет возрастать (поперечный эффект Гаусса).Если магнитное поле направлено параллельно направлению тока, то наблюдаетсяпродольный эффект Гаусса. Следует отметить, что при продольном эффекте изменение магнитосопротивления незначительно, поэтому он не получил большого применения.
Рис. 3.4
Зависимость удельного сопротивления от магнитной индукции в большом диапазоне изменения индукции можно описать формулой
, (3.17)
где ρ0 – удельное сопротивление приВ= 0;А– постоянная.
Из (3.17) следует, что при малых В(μ.В << 1) удельное сопротивлениеρквадратично зависит от индукцииВ, а при больших значениях индукции удельное сопротивление достигает насыщения.
Изменение удельного сопротивления от магнитной индукции Вможет быть описано также приближенной формулой [19]
, (3.18)
где n= (1–2) – в зависимости от величины (μВ).
Магниторезистивный эффект зависит также от направления магнитного поля и размеров образца. Эффект наиболее ярко выражен у пластин, имеющих форму диска Корбино, а также у некоторых сложных конфигураций.
Эффект Гаусса широко используется при построении датчиков магнитного поля, магниторезистивных датчиков.
3.1.4. Эффект Зеебека Эффект Зеебека– возникновение эдс в цепи, состоящей из двух разных проводников (или полупроводников), соединенных концами при различной температуре мест их соединений.
С
Рис. 3.5
труктурная схема эффекта Зеебека показана на рис. 3.5. Если взять проводник, концы которого имеют разные температуры, то от теплого конца к холодному будет передаваться тепловая энергия. Градиент температур приводит к появлению в проводнике электрического поля, обусловленного эффектом Томсона, который заключается в поглощении или высвобождении тепла линейно пропорционально току, проходящего через однородный проводник, имеющий градиент температуры вдоль его длины. Индуцированное электрическое поле приводит к появлению разности потенциалов [21], которая для однородного материала может быть найдена как, (3.19)
где α1 – абсолютный коэффициент Зеебека;dT– градиент температур.
Уравнение (3.19) является основным математическим выражением для термоэлектрического эффекта.
а б в
Рис. 3.6
В таком контуре индуцированная теплом разность потенциалов (термоЭДС) называется напряжением Зеебека и образуется тремя составляющими:
1) объемной, обусловленной возникновением разности потенциалов на концах проводника (полупроводника), имеющих разную температуру. Это объясняется тем, что носители зарядов на горячем конце приобретают более высокие энергии и скорости, и они диффундируют к холодному концу. В результате основные носители накапливаются на холодном конце проводника, а на горячем возникает потенциал противоположного знака;
2) контактной, обусловленной температурной зависимостью контактной разности потенциалов мест соединения проводников;
3) фононной, обусловленной увлечением электронов фононами, при превалирующем перемещении последних от горячего конца к холодному. Фононы сталкиваются с основными носителями заряда и увлекают их за собой. При низких температурах фононная составляющая может быть в десятки и сотни раз больше первых двух.
Напряжение Зеебека можно записать в виде степенного ряда от разности температур:
, (3.20)
где
Для большинства материалов требуется примерно восемь коэффициентов αi, чтобы получить погрешность определения термоЭДС не более ±1 % .
Для многих комбинаций материалов в узком интервале температур можно считать, что
, (3.21)
где α1 – коэффициент Зеебека.
Законы термоэлектрического контура
1. Для получения термоЭДС контур должен состоять из разнородных материалов (проводников или полупроводников).
2. Алгебраическая сумма всех термоЭДС в контуре, состоящем из любого количества соединений разных материалов, будет всегда равна нулю, если все соединения находятся при одинаковых температурах.
Это значит, что при включении в любое плечо контура дополнительного материала С (рис. 3.6б) результирующая термоЭДС в контуре не изменится при условии, что оба новых соединения будут иметь одинаковую температуру. Отсюда следует, что термоэлектрический контур можно разомкнуть в любом месте и включить в него дополнительные материалы. Количество дополнительных материалов неограничено, необходимо поддерживать только одинаковую температуру в местах их соединений. Термоэлектрические соединения могут выполняться любым способом: сваркой, пайкой, скруткой, сплавлением и т. д.
Таким образом, если известны термоЭДС (Е1 и Е2) двух проводников А и В при их подсоединении к третьему проводнику С, то результирующее напряжение при непосредственном контакте проводников (А и В) будет равно алгебраической сумме термоЭДС Е1 и Е2:
. (3.22)
3. Если два соединения разных материалов,
находящихся при температурах Т и Т1,
вырабатывают термоЭДС ЕТ1, а при
температурах Т1и Т
В табл. 3.3 приведены значения коэффициента термоЭДС некоторых материалов по отношению к платине (при 100 0С) [6].
Таблица 3.3
Материал | Кремний | Железо | Константан | Молибденит |
ТермоЭДС, мВ | +44 | +1,8 | -3,4 | -69 … -104 |
В простейшем случае, когда цепь состоит из двух проводников или полупроводников, она называется термоэлектрическим преобразователем, или термопарой. Проводники или полупроводники, составляющие термопару, называются термоэлектродами, а места их соединения – спаями. Спай термопары, воспринимающий измеряемую температуру Т, называется рабочим (горячим) спаем. Второго спая обычно нет, а есть два так называемых «свободных» конца, с которых снимается термоЭДС.
Третий закон позволяет градуировать (калибровать) термопару в одном температурном диапазоне, а использовать в другом [20], и его называют законом промежуточных температур.
Эффект Зеебека нашел широкое применения в области измерения температуры, в частности в термоэлектрических преобразователях.
studfiles.net
Эффект Гаусса. Диск Корбино — Мегаобучалка
Механизмы поглощения света в полупроводниках.
В полупроводниках имеются следующие четыре основных механизма поглощения света: 1. Поглощение на свободных носителях заряда. Для обозначения этого вида поглощения света иногда используется термин «друдевское» поглощение. Этот механизм поглощения связан с движением электронов в зоне проводимости и дырок в валентной зоне. Это движение из-за рассеяния носителей заряда приводит к ненулевой действительной части проводимости, которая и ответственна за поглощение.
3. Примесное поглощение света. При примесном поглощение начальное или конечное (или оба из них) состояние электрона в процессе поглощения света является связанным на примеси (доноре или акцепторе). 4. Решеточное поглощение света. В этом случае энергия света переходит в энергию колебаний решетки. Кроме того, свет может при определенных условиях поглощаться за счет взаимодействия с такими элементарными возбуждениями как плазмоны, магноны и др. Иногда в отдельный класс поглощения света выделяют процессы поглощения света в присутствии сильного магнитного поля (магнетопоглощение).
Люминесценция в полупроводниках при прямых фундаментальных переходах
Люминесценция является процессом, обратным поглощению, т. е. случаем, когда полупроводник, находящийся в возбужденном состоянии, испускает электромагнитное излучение.
Согласно принципу Франка—Кондона, спектр люминесценции, как правило, смещен в сторону длинных волн по сравнению с длиной волны возбуждения света.
Длительность спонтанного свечения определяется временем жизни носителей в возбужденном состоянии. В случае мономолекулярной релаксации возбужденных состояний I Л ~ I 0 e— t / τ . При большом уровне возбуждения интенсивность люминесценции описывается выражением
I = I0 /(1+ βt )2
где β — константа, зависящая от степени предварительного возбуждения. В случае такой зависимости считают, что люминесценция идет по бимолекулярному механизму. По аналогии с процессом поглощения рассмотрим рекомбинационное излучение полупроводников при фундаментальных переходах, которое возникает при непосредственной рекомбинации свободных носителей, при аннигиляции экситонов, а также при излучательной рекомбинации носителей через рекомбинационные ловушки, которые выступают в качестве центров свечения.
Прямые переходы наиболее вероятны. С ростом температуры в незаполненных зонах заполняются все более высоколежащие состояния и в спектре люминесценции появляется коротковолновый «хвост».
В примесных полупроводниках люминесценция идет преимущественно через локализованные центры рекомбинации. Отметим, кто при рекомбинации донор — акцептор последние необходимо рассматривать как неподвижную молекулу, помещенную в кристалл:
hυ=ΔE-EA-ED+e2/ε2
т. е. кулоново взаимодействие между донором и акцептором, находящихся в среде с диэлектрической проницаемостью ε , вызывает уменьшение их энергии связи на величину
ΔE кул = e2 / ε2
В зависимости от узлов кристаллической решетки, которые занимают доноры и акцепторы, существуют различные виды активных центров. Для получения стимулированного излучения в полупроводниках система должна находиться в состоянии с инверсной заселенностью. При этом
Fn — Fp > hυ
Fn — Fp > ΔE
где Fn и Fp , — положения квазиуровня Ферми для электронов и дырок соответственно. В таком случае система прозрачна на длине волны излучения. Состояние с инверсной заселенностью в полупроводниках может быть создано инжекцией неосновных носителей через p — n переход за счет возбуждения материала электромагнитным излучением, облучением электронами высоких энергий, ударной ионизацией в сильном электрическом поле.
Эффект Гаусса. Диск Корбино
Эффект Гаусса – эффект зависимости удельного сопротивления полупроводника (металла), помещенного в магнитное поле, от значения индукции этого поля.
Такая зависимость объясняется тем, что носители заряда (фермионы), перемещающиеся в полупроводнике (металле) под действием электрического поля, обладают не одинаковыми значениями скорости перемещения, так как известно, что скорости носителей заряда подчиняются распределению, отвечающему статистике Ферми-Дирака:
где EF – энергия Ферми; Ei – энергия i-го состояния фермиона; k – постоянная Больцмана; T – абсолютная температура.
В результате, наводимое поперечное поле Холла (4.1) компенсирует влияние силы Лоренца только на носители тока, имеющие некоторую скорость v (рис. 4.1). Траектория же носителей тока, скорость которых отлична от v, будет искривляться, приобретая дугообразную форму (рис. 1.1).
Такое искривление траекторий движения заряженных частиц приводит к увеличению числа их столкновений (сокращению длины свободного пробега), а, следовательно, – к понижению значения удельной проводимости и увеличению удельного сопротивления проводника или полупроводника (так называемый «физический эффект магнитосопротивления»).
где Δρ – приращение удельного сопротивления; ρ0 – удельное сопротивление материала вне магнитного поля; σ0 – удельная электрическая проводимость материала вне магнитного поля; σB – удельная электрическая проводимость в магнитном поле с индукцией B; μn – подвижность носителей заряда [12].
Естественно, что понятия слабого и сильного магнитных полей относительны, поскольку в условия μB<< 1 и μB>> 1 кроме магнитной индукции B, входит значение подвижности носителей заряда μ. Таким образом, сильное для полупроводников с высокой подвижностью электронов магнитное поле может являться слабым для полупроводников с меньшей подвижностью.
(4.9)
где A – коэффициент формы магниторезистора, при условии выражения подвижности носителей в единицах [см2·В-1·см-1], принимающий значение порядка ~10-12.
Из выражения (4.9) следует, что при малых значениях магнитной индукции, величина ∆ρ/ρ0 квадратично зависит от B, тогда как при больших значениях Bотношение ∆ρ/ρ0 достигает насыщения.
В инженерной практике для оценки относительного изменения сопротивления полупроводника в магнитном поле также часто используется следующее выражение:
(4.10)
где n – показатель степени, принимающий значения от 1 до 2, в зависимости от величины магнитной индукции.
Оптимальными геометрическими размерами, с точки зрения эффективности магниторезистивного эффекта, обладает так называемый диск Корбино – металлический или полупроводниковый диск, в котором один из электродов находится в центре диска, а другой расположен по длине его окружности (рис. 4.3). При такой конструкции магниторезистора, разность потенциалов Холла не возникает, так как отсутствуют грани, на которых могло бы происходить накопление заряда [13].
Здесь вне действия магнитного поля ток в образце направлен радиально. При помещении диска в магнитное поле B, вектор индукции которого перпендикулярен поверхности диска, носители тока будут отклоняться от изначальных радиальных прямых, вследствие чего траектория их движения будет удлиняться, но образование холловского поля, как было отмечено ранее – не происходит.
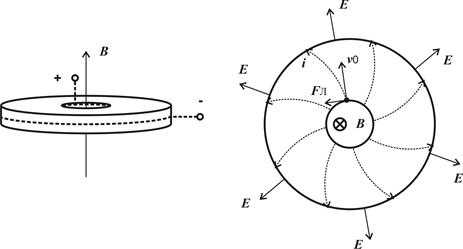
Рис. 4.3. Диск Корбино
В случае, когда проводимость диска Корбино обеспечивается зарядами одного знака, изменение его сопротивления рассчитывается как:
В другом случае, если в проводимости материала принимают участие и электроны и дырки, эффект изменения его удельного сопротивления будет определяться согласно выражению (4.12) [14].
(4.12)
где ε – отношение подвижности электронов к подвижности дырок; æ – отношение концентрации электронов к концентрации дырок.
В этом случае эффект Гаусса велик, так как электрическое поле Холла не противодействует силе Лоренца для носителей обоих типов.
Относительное изменение удельного сопротивления диска Корбино, изготовленного из полупроводника смешанной проводимости, определяется выражением (4.13) [12], [15].
(4.13)
Удельное сопротивление диска Корбино ρ никогда не бывает меньше удельного сопротивления образца ρB с a > b, но в некоторых случаях эти сопротивления могут быть равны. Выражение, связывающее их, имеет вид:
ρ = ρB(1+tan(θ)),
где θ – угол Холла (угол между направлением тока i и вектором суммарного поля E, т. е. угол отклонения носителей тока в результате эффекта Холла), рассчитываемый по формуле:
При θ=0 коэффициент Холла и поле Холла обращаются в ноль, и геометрические эффекты исчезают. Это возможно, при условии: ε=æ=1, тогда равенство соблюдается для всех значений B. Кроме этого, удельное сопротивление диска Корбино и магниторезистивное сопротивление образца прямоугольной формы совпадают при выполнении условия:
(4.14)
Выполнение условия (4.14) имеет место в полупроводниках с проводимостью p – типа, если ε > 1. В этом случае угол Холла меняет знак при увеличении магнитного поля и при некотором значении напряженности поля коэффициент Холла обращается в нуль.
megaobuchalka.ru
Эффект — гаусс — Большая Энциклопедия Нефти и Газа, статья, страница 1
Эффект — гаусс
Cтраница 1
Эффект Гаусса максимален у полупроводниковых материалов с большими подвижностями носителей тока, но такие материалы, как правило, обладают малым удельным сопротивлением, поэтому, чтобы повысить омическое сопротивление магниторезиеторов, их необходимо делать в виде тонких нитей. Примером могут быть висмутовые спирали магниторезиеторов, используемые для измерения сильных магнитных полей. [1]
Эффект Гаусса может быть использован для измерения добротности радиочастотных контуров. Для этого магниторезисторы включаются в фазосдвигающие цепочки С-автогенератора и питаются током, протекающим через катушку. [2]
Техническое использование эффекта Гаусса выдвигает качественные требования к полупроводниковым материалам. [3]
В этом случае эффект Гаусса велик, так как электрическое поле Холла не может противодействовать силе Лоренца для носителей обоих типов. [4]
В первом случае эффект Гаусса проявляется наиболее полно, ибо при протекании тока через диск в радиальном направлении эффект Холла практически отсутствует. [5]
Магниторезистивный эффект, ил-и эффект Гаусса, заключается в изменении удельной проводимости полупроводника при изменении воздействующего на него магнитного поля. [6]
Особенно полезным является использование эффекта Гаусса в приборах типа умножителей, усилителей тока генераторов электрических колебаний, измерителей магнитного поля и неэлектрических величин. Развитие техники производства полупроводниковых материалов с высокой подвижностью носителей тока и заданной структурой ( как, например, эвтектические сплавы ан-тимонида индия и антимонида никеля) способствует созданию магниторезисторов с большим относительным изменением сопротивления в магнитном поле. При этом значительно может быть упрощена технология производства магниторезисторов. Малые размеры резисторов, простая форма и легкость изготовления позволяют использовать их При миниатюризации аппаратуры. [7]
Влияние формы полупроводниковой пластины на эффект Гаусса может быть уменьшено, если измерения провести на длинном тонком стержне. Тем не менее, неоднородности распределения примесей также влияют на гальваномагнитные эффекты, правда, менее явно, чем форма полупроводниковой пластины магниторезистора. Так, например, монокристаллы антимонида индия с примесью железа дают сильную анизотропию поперечного изменения сопротивления в магнитном поле даже тогда, когда неоднородность не обнаруживается при холловских измерениях. [8]
Магниторезистивный эффект, называемый также эффектом Гаусса, заключается в изменении электрического сопротивления под воздействием магнитного поля. Он обусловлен изменением пути, проходимого носителями заряда между актами рассеяния, при наличии магнитного поля. Дело в том, что даже при наличии поля Холла и в примесном полупроводнике вследствие теплового движения всегда есть носители заряда, движущиеся со скоростями, как большими, так и меньшими средней скорости дрейфа во внешнем электрическом поле. Таким образом, направление движения практически всех носителей заряда в магнитном поле не совпадает с направлением внешнего электрического поля. Магниторезистивный эффект считается положительным, если при воздействии магнитного поля сопротивление материала возрастает. [10]
Под названием эффект магнитосопротивления ( или эффект Гаусса) подразумевают наличие зависимости удельного сопротивления полупроводника от магнитного поля. [12]
Под названием эффект магнитосопротивления ( или эффект Гаусса) подразумевают наличие зависимости удельного сопротивления полупроводника от магнитного поля. [14]
Принцип действия этих преобразователей основан на эффекте Гаусса, заключающемся в уменьшении подвижности носителей тока в магнитном поле. Под действием магнитного поля траектория носителей тока искривляется, в результате чего скорость их движения в направлении электрического поля уменьшается. Это равносильно уменьшению подвижности носителей тока и увеличению электрического сопротивления преобразователя. [15]
Страницы: 1 2 3 4
www.ngpedia.ru
3.1.5. Пьезоэлектрический эффект
Различают прямой и обратный пьезоэлектрический эффект.
Прямой пьезоэлектрический эффект заключается в образовании в кристаллическом материале электрических зарядов при приложении к нему механических напряжений (рис. 3.7а).
а б
Рис. 3.7
Обратный пьезоэлектрический эффект заключается в изменении размеров диэлектрика при приложении к нему электрического поля (рис. 3.7б).
Пьезоэлектрический эффект наблюдается в природных кристаллах, таких как кварц (SiO2), поляризованных керамических материалах и некоторых полимерах, например поливинилиденфториде. Вещества, у которых наблюдаются такие свойства, называются пьезоэлектриками.
Физическую природу пьезоэлектрического
эффекта рассмотрим на примере
пьезоэлектрического кристалла –
кварца. В кристалле кварца можно выделить
три главные оси (рис. 3.8а): продольную
(оптическую ось) Z; электрическую ось Х
(три оси, сдвинутые на 1200),
механическую Y (три оси, сдвинутые на
1200). Электрические оси Х проходят
через центр и соединяют два разнополярных
иона. Кристалл кварца можно представить
в виде элементарных ячеек (рис. 3.8б),
состоящих из атомовSi,
обладающих положительным зарядом, и
спаренных атомов О2, обладающих
отрицательным зарядом. По электрическим
осям Х направлены векторы поляризации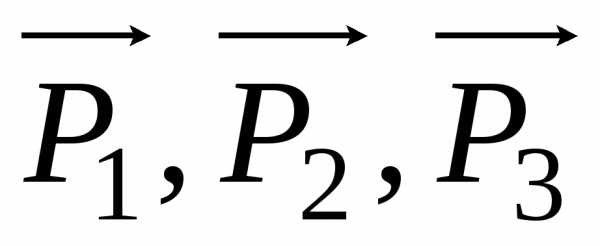 .
Без приложения механических напряжений
сумма векторов
.
Без приложения механических напряжений
сумма векторов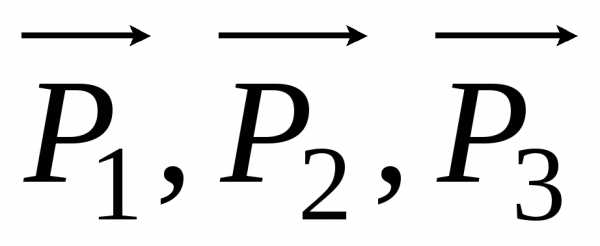 равна нулю, т. е. кварцевая ячейка является
электрически нейтральной.
равна нулю, т. е. кварцевая ячейка является
электрически нейтральной.
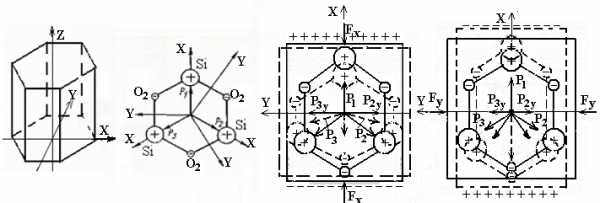
а б в г
Рис. 3.8
Если к кристаллу кварца
вдоль оси X
приложена сила Fx,
равномерно распределенная по грани,
перпендикулярной оси X, то в результате
деформации элементарной ячейки ее
электрическая нейтральность нарушается.
При этом, как показано на рис. 3.8в,
сдавливающая сила сдвигает атомы
кристалла таким образом, что положительный
атом кремния перемещается в одну сторону
решетки, а отрицательно заряженная пара
атомов кислорода – в другую. В результате
чего вдоль оси Y
происходит перераспределение зарядов,
т. е. в деформированном состоянии ячейки
сумма проекций векторов  и
и 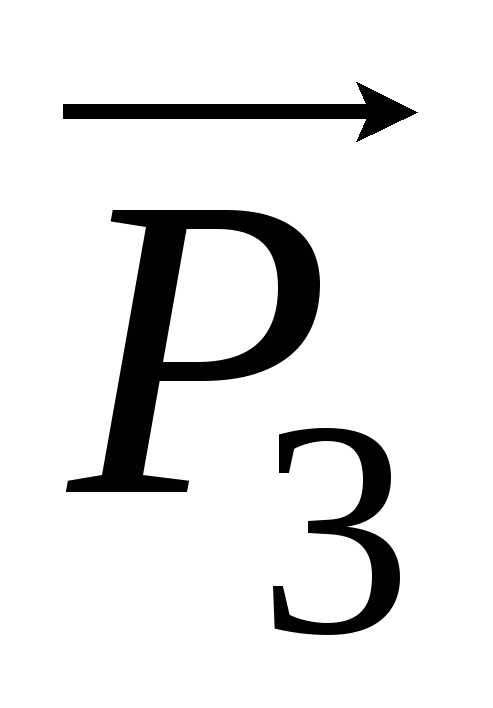 на ось X становится меньше
(при сжатии) или больше (при растяжении)
вектора
на ось X становится меньше
(при сжатии) или больше (при растяжении)
вектора  . В результате появляется
равнодействующая вектора поляризации,
ей соответствуют поляризационные
заряды на гранях, знаки которых для
сжатия показаны на рис. 3.8в. При этом деформация
ячейки не влияет на электрическое
состояние вдоль оси Y, сумма проекций
векторов
. В результате появляется
равнодействующая вектора поляризации,
ей соответствуют поляризационные
заряды на гранях, знаки которых для
сжатия показаны на рис. 3.8в. При этом деформация
ячейки не влияет на электрическое
состояние вдоль оси Y, сумма проекций
векторов 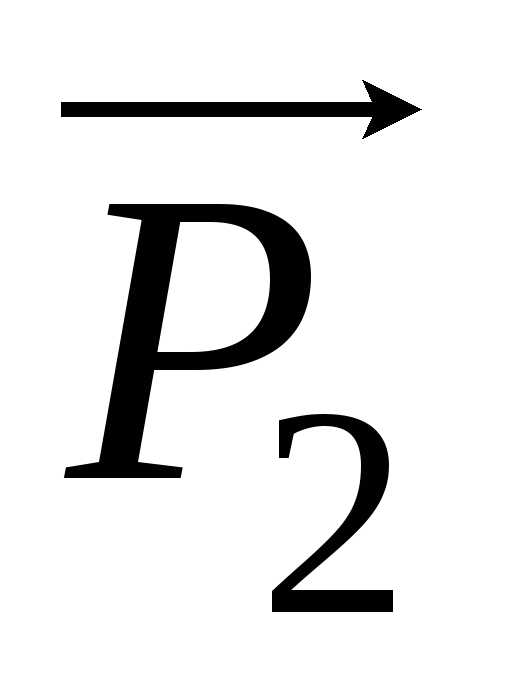 и
и 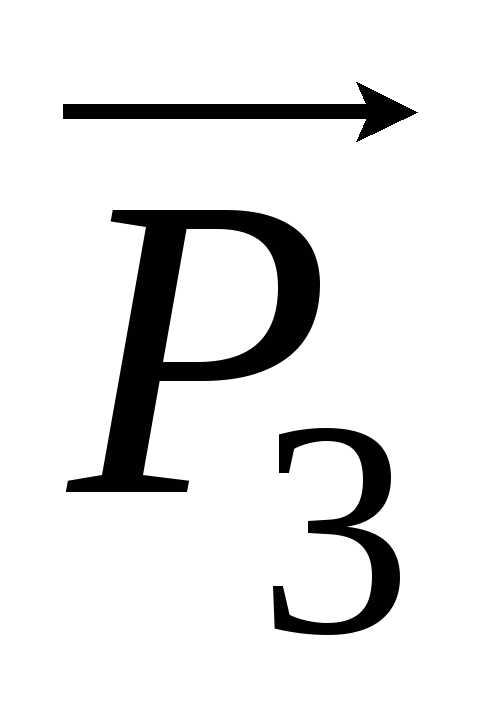 на ось Y
равна нулю, ибо Р2Y= Р3Y.
на ось Y
равна нулю, ибо Р2Y= Р3Y.
Образование поляризационных зарядов на гранях, перпендикулярных оси X, при действии силы по оси X называется продольным пьезоэлектрическим эффектом.
При механических напряжениях,
приложенных вдоль одной из механических
осей Y (рис. 3.8г), геометрическая
сумма проекций векторов  и
и 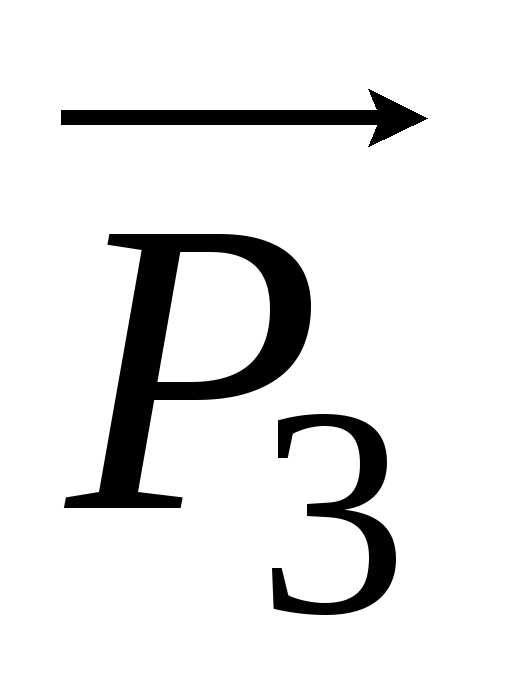 на ось Y равна нулю, и на гранях
пьезоэлемента, перпендикулярных оси Y, заряды не образуются.
При этом сумма проекций векторов
на ось Y равна нулю, и на гранях
пьезоэлемента, перпендикулярных оси Y, заряды не образуются.
При этом сумма проекций векторов 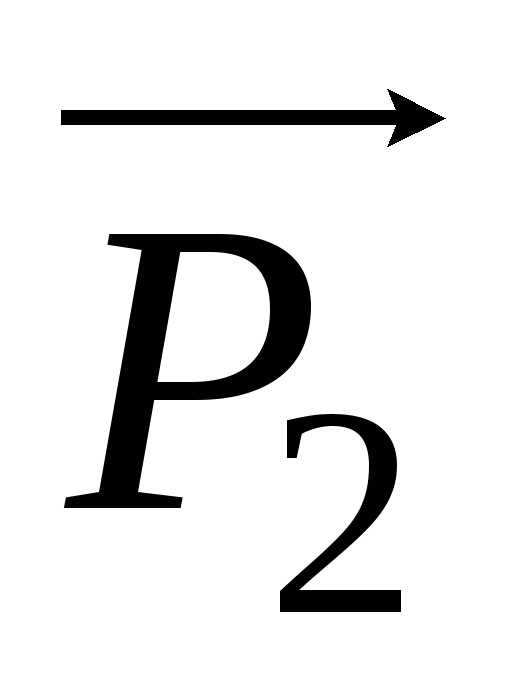 и
и 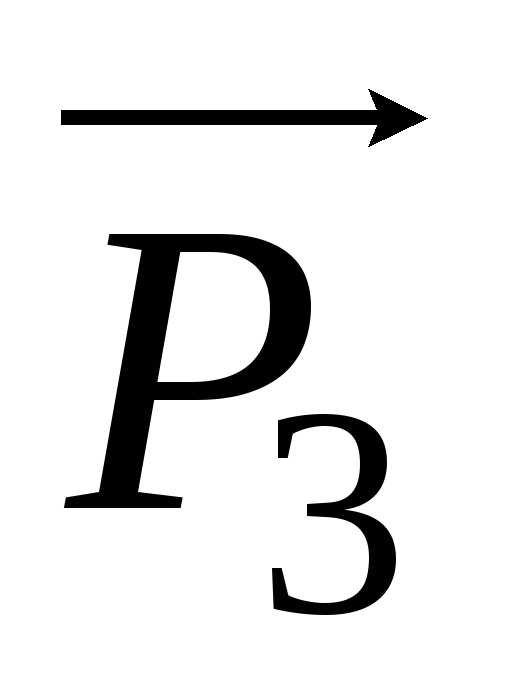 на ось X оказывается не равной
вектору
на ось X оказывается не равной
вектору 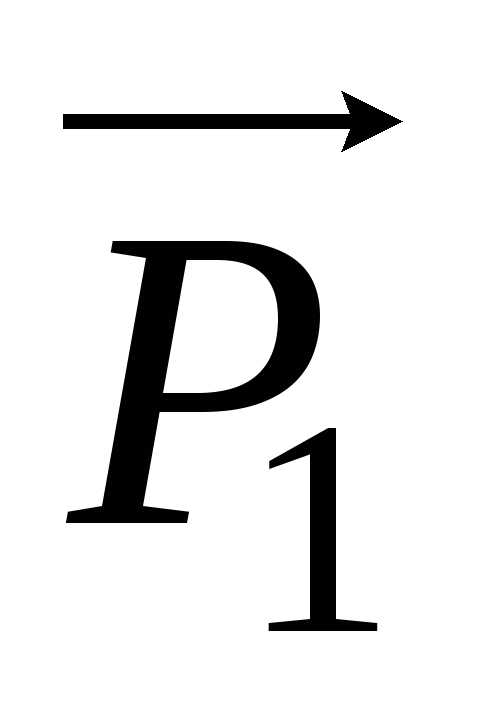 . В результате появляется
равнодействующая вектора поляризации,
ей соответствуют поляризационные
заряды на гранях, знаки которых для
сжатия показаны на рис. 3.8г.
. В результате появляется
равнодействующая вектора поляризации,
ей соответствуют поляризационные
заряды на гранях, знаки которых для
сжатия показаны на рис. 3.8г.
Эффект образования зарядов на гранях, перпендикулярных нагружаемым граням, называется поперечным пьезоэлектрическим эффектом (например, при действии силы по оси Y образуются поляризационные заряды на гранях, перпендикулярных оси X).
При равномерном нагружении со всех сторон (например, гидростатическом сжатии) кристалл кварца остается электрически нейтральным. При нагружении по оси Z, перпендикулярной осям X и Y и называемой оптической осью, кристалл кварца также остается электрически нейтральным.
При механическом напряжении
сдвига геометрическая сумма проекций
векторов 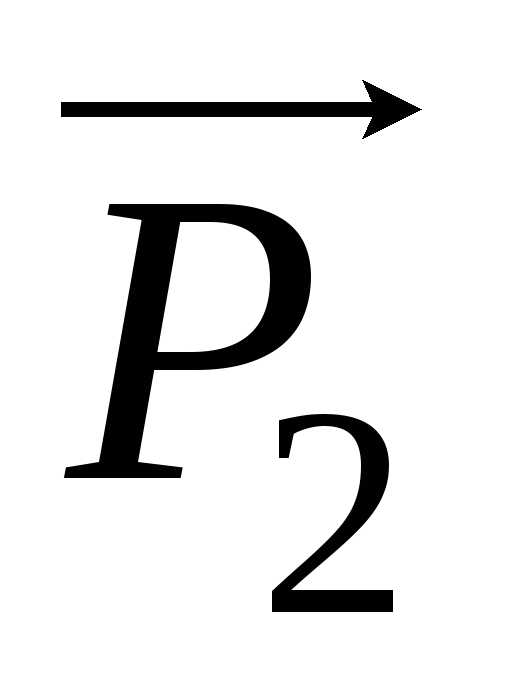 и
и 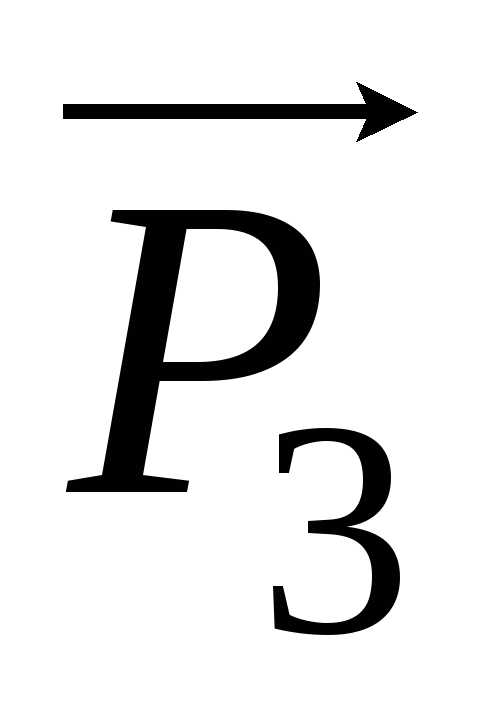 на ось X равна вектору
на ось X равна вектору 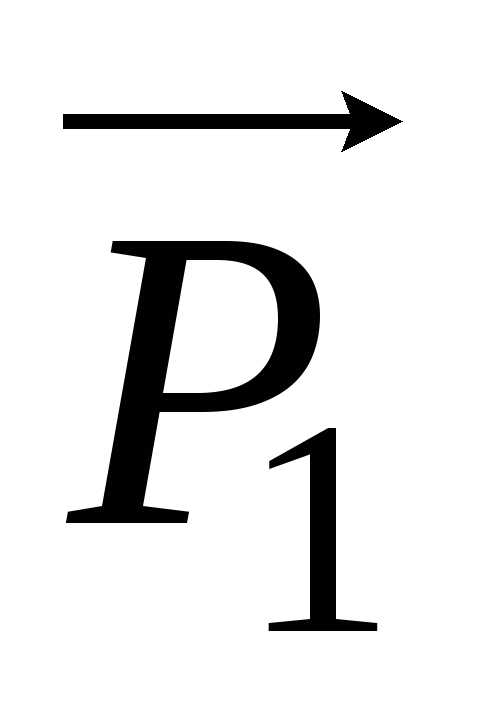 ,
направленному по оси X, и на гранях,
перпендикулярных оси X, заряд не возникает.
Однако проекции векторов
,
направленному по оси X, и на гранях,
перпендикулярных оси X, заряд не возникает.
Однако проекции векторов 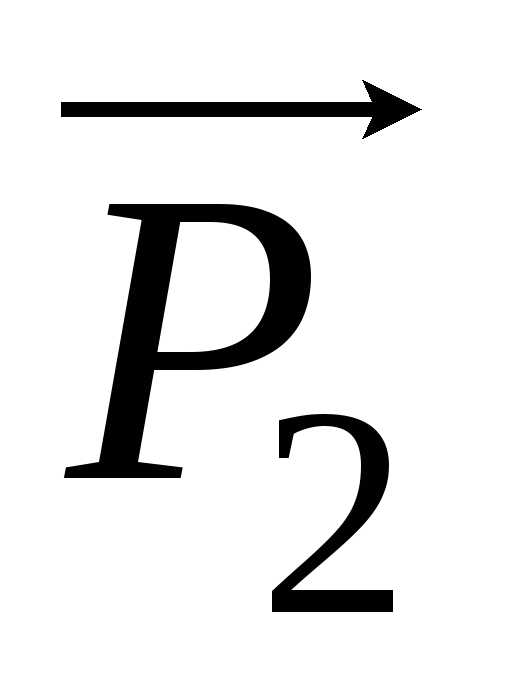 и
и 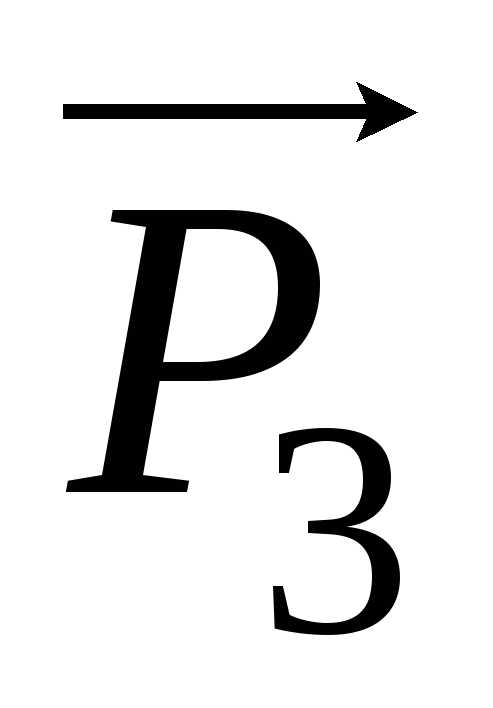 на ось Y
не равны, и на гранях, перпендикулярных
оси Y,
возникает заряд.
на ось Y
не равны, и на гранях, перпендикулярных
оси Y,
возникает заряд.
В общем пьезоэлектрический эффект можно оценить через вектор поляризации [20] как
(3.23)
где x,y,z– координатные оси обычной ортогональной системы, совмещенные с осями кристалла.
(3.24)
где σ– осевое напряжение;dik– постоянные пьезоэлектрические коэффициенты вдоль ортогональных осей срезов кристалла(пьезоэлектрическая постоянная, пьезомодуль).
Если из кристалла кварца вырезать параллелепипед так, чтобы его грани были перпендикулярны осям X-Y (рис. 3.9), то под действием силы FXв направлении оси X (продольный пьезоэффект) на гранях, параллельных оси Y, появится зарядQ, который находится как
, (3.25)
где δх – поверхностная плотность заряда; Sх – пло-щадь грани, на которой образуется заряд; d11 – пьезоэлектрическая постоянная (пьезомодуль).
П
Рис. 3.9
ри продольном пьезоэффекте заряд не зависит от размеров образца (пьезоэлемента). При поперечном пьезоэффекте заряд может быть увеличен соответствующим выбором размеров пьезоэлемента, т. е. длин реберl и b:. (3.26)
Пьезоэлектрические кристаллы являются прямыми преобразователями механической энергии в электрическую. Эффективность такого преобразования может быть выражена через коэффициент электромеханической связи kik:
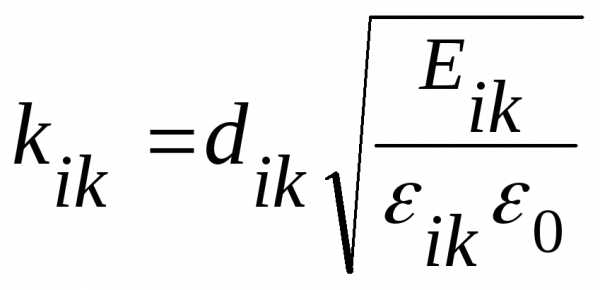 .
(3.27)
.
(3.27)
Этот коэффициент является важной характеристикой для случаев, когда необходимо обеспечить высокую эффективность передачи энергии, например в акустических и ультразвуковых датчиках.
Пьезоэлектрический эффект используется для построения датчиков различных физических величин: силы, давления, акустических величин и др.
В табл. 3.4 приведены характеристики некоторых пьезоэлектрических материалов.
Таблица 3.4
Материал | Диэлектрическая проницаемость ε | Пьезомодуль d. 1012, Кл/Н | Модуль упругости Е, ГПа | Коэффициент электромеханической связи k |
Кварц | 4,5(11) | 2,31(11) | 86,7(11) | 0,095 |
Титанат бария ТБ-1 | 1500 | 45(11) | 100–110 | 0,2(11) |
100(33) | 0,5(11) | |||
Группа ЦТС | 1100 | 75(11) | 108–116 | 0,2(11) |
113(33) | 0,41(11) | |||
Сульфат лития | 10,3 | 16(22) | 62(22) | 0,38 |
studfiles.net
Пушка Гаусса — это… Что такое Пушка Гаусса?
Иллюстрация принципа действияПушка Гаусса (англ. Gauss gun, Coil gun, Gauss cannon) — одна из разновидностей электромагнитного ускорителя масс. Названа по имени немецкого учёного Карла Гаусса, заложившего основы математической теории электромагнетизма. Следует иметь ввиду, что данный метод ускорения масс используется в основном в любительских установках, так как данный метод не является достаточно эффективным для практической реализации. По своему принципу работы (создание бегущего магнитного поля) сходна с устройством известным как линейный двигатель.
Принцип действия
Пушка Гаусса состоит из соленоида, внутри которого находится ствол (как правило, из диэлектрика). В один из концов ствола вставляется снаряд (сделанный из ферромагнетика). При протекании электрического тока в соленоиде возникает магнитное поле, которое разгоняет снаряд, «втягивая» его внутрь соленоида. На концах снаряда при этом образуются полюса, ориентированные согласно полюсам катушки, из-за чего после прохода центра соленоида снаряд притягивается в обратном направлении, то есть тормозится. В любительских схемах иногда в качестве снаряда используют постоянный магнит так как с возникающей при этом ЭДС индукции легче бороться. Такой же эффект возникает при использовании ферромагнетиков, но выражен он не так ярко благодаря тому что снаряд легко перемагничивается (коэрцитивная сила).
Для наибольшего эффекта импульс тока в соленоиде должен быть кратковременным и мощным. Как правило, для получения такого импульса используются электролитические конденсаторы с высоким рабочим напряжением.
Параметры ускоряющих катушек, снаряда и конденсаторов должны быть согласованы таким образом, чтобы при выстреле к моменту подлета снаряда к соленоиду индукция магнитного поля в соленоиде была максимальна, но при дальнейшем приближении снаряда резко падала. Стоит заметить что возможны разные алгоритмы работы ускоряющих катушек.
- Кинетическая энергия снаряда
— масса снаряда
— его скорость
- Энергия запасаемая в конденсаторе
— напряжение конденсатора
— ёмкость конденсатора
- Время разряда конденсаторов
Это время за которое конденсатор полностью разряжается. Оно равно четверти периода:
— индуктивность
— ёмкость
- Время работы катушки индуктивности
Это время за которое ЭДС катушки индуктивности возрастает до максимального значения (полный разряд конденсатора) и полностью падает до 0. Оно равно верхнему полупериоду синусоиды.
— индуктивность
— ёмкость
Применение
Теоретически возможно применение пушек Гаусса для запуска лёгких спутников на орбиту. Основное применение — любительские установки, демонстрация свойств ферромагнетиков. Также достаточно активно используется в качестве детской игрушки или развивающей техническое творчество самодельной установки (простота и относительная безопасность).
Преимущества и недостатки
Пушка Гаусса в качестве оружия обладает преимуществами, которыми не обладают другие виды стрелкового оружия. Это отсутствие гильз и неограниченность в выборе начальной скорости и энергии боеприпаса, возможность бесшумного выстрела (если скорость достаточно обтекаемого снаряда не превышает скорости звука) в том числе без смены ствола и боеприпаса, относительно малая отдача (равная импульсу вылетевшего снаряда, нет дополнительного импульса от пороховых газов или движущихся частей), теоретически, больша́я надежность и теоретически износостойкость, а также возможность работы в любых условиях, в том числе в космическом пространстве.
Однако, несмотря на кажущуюся простоту пушки Гаусса, использование её в качестве оружия сопряжено с серьёзными трудностями.
Первая и основная трудность — низкий КПД установки. Лишь 1-7 % заряда конденсаторов переходят в кинетическую энергию снаряда. Отчасти этот недостаток можно компенсировать использованием многоступенчатой системы разгона снаряда, но в любом случае КПД редко достигает 27 %. В основном в любительских установках энергия запасенная в виде магнитного поля никак не используется, а является причиной использования мощных ключей (часто применят доступные IGBT модули) для размыкания катушки (правило Ленца).
Вторая трудность — большой расход энергии (из-за низкого КПД).
Третья трудность (следует из первых двух) — большой вес и габариты установки при её низкой эффективности.
Четвёртая трудность — достаточно длительное время накопительной перезарядки конденсаторов, что заставляет вместе с пушкой Гаусса носить и источник питания (как правило, мощную аккумуляторную батарею), а также высокая их стоимость. Можно, теоретически, увеличить эффективность, если использовать сверхпроводящие соленоиды, однако это потребует мощной системы охлаждения, что приносит дополнительные проблемы, и серьёзно влияет на область применения установки.
Пятая трудность — с увеличением скорости снаряда время действия магнитного поля, за время пролёта снарядом соленоида, существенно сокращается, что приводит к необходимости не только заблаговременно включать каждую следующую катушку многоступенчатой системы, но и увеличивать мощность её поля пропорционально сокращению этого времени. Обычно этот недостаток сразу обходится вниманием, так как большинство самодельных систем имеет или малое число катушек, или недостаточную скорость пули.
В условиях водной среды применение пушки без защитного кожуха также серьезно ограничено — дистанционной индукции тока достаточно, чтобы раствор солей диссоциировал на кожухе с образованием агрессивных (растворяющих) сред что требует дополнительного магнитного экранирования.
Таким образом, на сегодняшний день у пушки Гаусса нет перспектив в качестве оружия, так как она значительно уступает другим видам стрелкового оружия, и вряд ли перспективы появятся в будущем, так как она не может составить конкуренцию установкам, работающим на других принципах. Теоретически, перспективы возможны лишь в будущем, если будут созданы компактные и мощные источники электрического тока и высокотемпературные сверхпроводники (200—300К). Однако, установка, подобная пушке Гаусса, может использоваться в космическом пространстве, так как в условиях вакуума и невесомости многие недостатки подобных установок нивелируются. В частности, в военных программах СССР и США рассматривалась возможность использования установок, подобных пушке Гаусса, на орбитальных спутниках для поражения других космических аппаратов (снарядами с большим количеством мелких поражающих деталей), или объектов на земной поверхности.
В литературе
Довольно часто в литературе научно-фантастического жанра упоминается пушка Гаусса. Она выступает там в роли высокоточного смертоносного оружия. Примером такого литературного произведения являются книги из серии «S.T.A.L.K.E.R.», написанные по серии игр S.T.A.L.K.E.R., где Гаусс-пушка была одним из мощнейших видов оружия. Но первым в научной фантастике пушку Гаусса воплотил в реальность Гарри Гаррисон в своей книге «Месть Стальной Крысы» (неправда, задолго до Гаррисона, А. Казанцев, «Пылающий остров», возможно, были ещё более ранние упоминания). Цитата из книги: «Каждый имел при себе гауссовку — многоцелевое и особо смертоносное оружие. Его мощные батареи накапливали впечатляющий заряд. Когда нажимали на спуск, в стволе генерировалось сильное магнитное поле, разгоняющее снаряд до скорости, не уступающей скорости снаряда любого другого оружия с реактивными патронами. Но гауссовка имела то превосходство, что обладала более высокой скорострельностью, была абсолютно бесшумной и стреляла любыми снарядами, от отравленных иголок до разрывных пуль.»
В компьютерных играх
- В игре Crimsonland присутствует пушка Гаусса, которая бесшумно пронизывает врагов, нанося тяжёлые повреждения.
- В Warzone 2100 при развитии до 70 % открывается доступ к пушке Гаусса.
- В BattleTech, в сериях MechWarrior и MechCommander.
- В стратегиях Command & Conquer 3: Tiberium Wars и Command & Conquer 3: Kane’s Wrath существует улучшение «Пушки Гаусса», увеличивающее урон для танков «Хищник» и «Мамонт», роботов «Титан» и защитных орудий «Страж». Также Спецназ ГСБ в игре вооружены Скорострельными Гаусс-винтовками.
- В игре S.T.A.L.K.E.R. гаусс-пушка имеет огромную мощность и медленно перезаряжается. Она работает на батареях, которые используют энергию артефакта «Вспышка». В игре «S.T.A.L.K.E.R Зов Припяти» под аномалией «Железный лес» есть помещение где проводились её испытание, там же стоит огромная пушка Гаусса.
- В «StarCraft» пехотинцы вооружены автоматической винтовкой Гаусса C-14 «Impaler». Призраки также имеют винтовки C-10, которые называются «Картечные винтовки».
- В «Crysis» винтовка Гаусса представляет собой снайперское оружие, наносящее максимальный урон.
- В «Crysis 2» пушка Гаусса представляет собой модификацию для штурмовой винтовки, наряду с подствольным гранатомётом. Обладает большим уроном и медленной перезарядкой.
- В «Fallout 2» винтовка Гаусса является самым мощным оружием с высокой дальностью стрельбы, почти не уступающей снайперским винтовкам.
- В «Fallout 3» и в «Fallout New Vegas» винтовка Гаусса — энергетическая снайперская винтовка, оснащённая оптическим прицелом и отличающаяся высокой эффективностью на средних и больших дистанциях. Наносит очень большой урон.
- В «Fallout Tactics» есть гаусс-пистолет, гаусс-винтовка и четырёхствольный гаусс-пулемёт.
- В игре X-COM: Terror From The Deep орудие Гаусса является одной из первых разработок для уничтожения инопланетян под водой.
- В играх X³: Reunion/X³: Terran Conflict Гаусс-пушка — мощное оружие для эсминцев, обладающее хорошей дальностью, но низкой скоростью полёта снарядов. Энергии практически не тратит, но требует специальных боеприпасов.
- B Ogame пушка Гаусса — мощное оборонительное сооружение.
- В Red Faction: Guerrilla Гауссова винтовка является оружием высокой мощности, но обладает средней разрушающей силой по сравнению с другими видами оружия, несущими разрушающий характер.
- В MMOTPS игре S4 League пушка Гаусса представляет из себя пулемет, у которого при беспрерывной стрельбе постепенно снижается точность.
- В серии игр Warhammer 40.000 пушки Гаусса активно используются некронами.
- Под пушкой Гаусса в этом случае подразумевается энергетическое оружие стреляющее зелеными молниями и разрушающее межмолекулярные связи, в некоторых случаях утверждается, что жертва подвергается аннигиляции.
См. также
Ссылки
Примечания
dic.academic.ru
Пушка Гаусса Википедия
Иллюстрация принципа стрельбыПушка Гаусса (англ. Gauss gun, Coil gun, Gauss cannon) — одна из разновидностей электромагнитного ускорителя масс. Названа по имени немецкого учёного Карла Гаусса, заложившего основы математической теории электромагнетизма. Следует иметь в виду, что этот метод ускорения масс используется в основном в любительских установках, так как не является достаточно эффективным для практической реализации. По своему принципу работы (создание бегущего магнитного поля) сходна с устройством, известным как линейный двигатель.
Принцип действия
Пушка Гаусса состоит из соленоида, внутри которого находится ствол (как правило, из диэлектрика). В один из концов ствола вставляется снаряд, сделанный из ферромагнетика. При протекании электрического тока в соленоиде возникает электромагнитное поле, которое разгоняет снаряд, «втягивая» его внутрь соленоида. На концах снаряда при этом образуются полюса, ориентированные согласно полюсам катушки, из-за чего после прохода центра соленоида снаряд притягивается в обратном направлении, то есть тормозится. В любительских схемах иногда в качестве снаряда используют постоянный магнит, так как с возникающей при этом ЭДС индукции легче бороться. Такой же эффект возникает при использовании ферромагнетиков, но выражен он не так ярко благодаря тому, что снаряд легко перемагничивается (коэрцитивная сила).
Для наибольшего эффекта импульс тока в соленоиде должен быть кратковременным и мощным. Как правило, для получения такого импульса используются электролитические конденсаторы большой ёмкости и с высоким рабочим напряжением.
Параметры ускоряющих катушек, снаряда и конденсаторов должны быть согласованы таким образом, чтобы при выстреле к моменту подлета снаряда к соленоиду индукция магнитного поля в соленоиде была максимальна, но при дальнейшем приближении снаряда резко падала. Стоит заметить, что возможны разные алгоритмы работы ускоряющих катушек.
- Кинетическая энергия снаряда
- E=mv22{\displaystyle E={mv^{2} \over 2}}
- m{\displaystyle m} — масса снаряда
- v{\displaystyle v} — его скорость
- Энергия, запасаемая в конденсаторе
- E=CU22{\displaystyle E={CU^{2} \over 2}}
- U{\displaystyle U} — напряжение конденсатора
- C{\displaystyle C} — ёмкость конденсатора
- Время разряда конденсаторов
Это время за которое конденсатор полностью разряжается:
- T=πLC2{\displaystyle T={\pi {\sqrt {LC}} \over 2}}
- L{\displaystyle L} — индуктивность
- C{\displaystyle C} — ёмкость
- Время работы катушки индуктивности
Это время за которое ЭДС катушки индуктивности возрастает до максимального значения (полный разряд конденсатора) и полностью падает до 0. Оно равно верхнему полупериоду синусоиды.
- T=2πLC{\displaystyle T=2\pi {\sqrt {LC}}}
- L{\displaystyle L} — индуктивность
- C{\displaystyle C} — ёмкость
Стоит заметить, что в представленном виде две последние формулы не могут применяться для расчетов пушки Гаусса, хотя бы по той причине, что по мере движения снаряда внутри катушки, её индуктивность все время изменяется.
Применение
Теоретически возможно применение пушек Гаусса для запуска лёгких спутников на орбиту так как при стационарном использовании есть возможность иметь большой источник энергии. Основное применение — любительские установки, демонстрация свойств ферромагнетиков. Также достаточно активно используется в качестве детской игрушки или развивающей техническое творчество самодельной установки (простота и относительная безопасность)
Создание
Простейшие конструкции могут быть собраны из подручных материалов даже при школьных знаниях физики[1]
Существует множество сайтов, в которых подробно описано, как собрать пушку Гаусса. Но стоит помнить, что создание оружия в некоторых странах может преследоваться по закону. Поэтому, перед тем, как создавать пушку Гаусса, стоит задуматься, как вы будете применять её.
Преимущества и недостатки
Пушка Гаусса в качестве оружия обладает преимуществами, которыми не обладают другие виды стрелкового оружия. Это отсутствие гильз и неограниченность в выборе начальной скорости и энергии боеприпаса, возможность бесшумного выстрела (если скорость достаточно обтекаемого снаряда не превышает скорости звука) в том числе без смены ствола и боеприпаса, относительно малая отдача (равная импульсу вылетевшего снаряда, нет дополнительного импульса от пороховых газов или движущихся частей), теоретически, больша́я надёжность и, в теории, износостойкость, а также возможность работы в любых условиях, в том числе в космическом пространстве.
Однако, несмотря на кажущуюся простоту пушки Гаусса, использование её в качестве оружия сопряжено с серьёзными трудностями, главное из которых: большие затраты энергии.
Первая и основная трудность — низкий КПД установки. Лишь 1-7 % заряда конденсаторов переходят в кинетическую энергию снаряда. Отчасти этот недостаток можно компенсировать использованием многоступенчатой системы разгона снаряда, но в любом случае КПД редко достигает 27 %. В основном в любительских установках энергия, запасённая в виде магнитного поля, никак не используется, а является причиной использования мощных ключей (часто применяют IGBT модули) для размыкания катушки (правило Ленца).
Вторая трудность — большой расход энергии (из-за низкого КПД).
Третья трудность (следует из первых двух) — большой вес и габариты установки при её низкой эффективности.
Четвёртая трудность — достаточно длительное время накопительной перезарядки конденсаторов, что заставляет вместе с пушкой Гаусса носить и источник питания (как правило, мощную аккумуляторную батарею), а также высокая их стоимость. Можно, теоретически, увеличить эффективность, если использовать сверхпроводящие соленоиды, однако это потребует мощной системы охлаждения, что приносит дополнительные проблемы, и серьёзно влияет на область применения установки. Или же использовать заменяемые батареи конденсаторы.
Пятая трудность — с увеличением скорости снаряда время действия магнитного поля, за время пролёта снарядом соленоида, существенно сокращается, что приводит к необходимости не только заблаговременно включать каждую следующую катушку многоступенчатой системы, но и увеличивать мощность её поля пропорционально сокращению этого времени. Обычно этот недостаток сразу обходится вниманием, так как большинство самодельных систем имеет или малое число катушек, или недостаточную скорость пули.
В условиях водной среды применение пушки без защитного кожуха также серьёзно ограничено — дистанционной индукции тока достаточно, чтобы раствор солей диссоциировал на кожухе с образованием агрессивных (растворяющих) сред, что требует дополнительного магнитного экранирования.
Таким образом, на сегодняшний день у пушки Гаусса нет перспектив в качестве оружия, так как она значительно уступает другим видам стрелкового оружия, работающего на других принципах. Теоретически, перспективы, конечно, возможны, если будут созданы компактные и мощные источники электрического тока и высокотемпературные сверхпроводники (200—300К). Однако, установка, подобная пушке Гаусса, может использоваться в космическом пространстве, так как в условиях вакуума и невесомости многие недостатки подобных установок нивелируются. В частности, в военных программах СССР и США рассматривалась возможность использования установок, подобных пушке Гаусса, на орбитальных спутниках для поражения других космических аппаратов (снарядами с большим количеством мелких поражающих деталей), или объектов на земной поверхности.
В литературе
Довольно часто в литературе научно-фантастического жанра упоминается пушка Гаусса. Она выступает там в роли высокоточного смертоносного оружия.
Примером такого литературного произведения являются книги из серии «S.T.A.L.K.E.R.», написанные по серии игр S.T.A.L.K.E.R., где Гаусс-пушка была одним из мощнейших видов оружия, не считая РПГ-7.
Но первым в научной фантастике пушку Гаусса воплотил в реальность Гарри Гаррисон в своей книге «Месть Стальной Крысы». Цитата из книги: «Каждый имел при себе гауссовку — многоцелевое и особо смертоносное оружие. Его мощные батареи накапливали впечатляющий заряд. Когда нажимали на спуск, в стволе генерировалось сильное магнитное поле, разгоняющее снаряд до скорости, не уступающей скорости снаряда любого другого оружия с реактивными патронами. Но гауссовка имела то превосходство, что обладала более высокой скорострельностью, была абсолютно бесшумной и стреляла любыми снарядами, от отравленных иголок до разрывных пуль».
См. также
Ссылки
Примечания
- ↑ Брага Н. Создание роботов в домашних условиях. — М.: НТ Пресс, 2007. — С. 141 — ISBN 5-477-00749-4.
wikiredia.ru
Эффект — гаусс — Большая Энциклопедия Нефти и Газа, статья, страница 3
Эффект — гаусс
Cтраница 3
Для измерения магнитной индукции и напряженности магнитного поля в настоящее время используют эффект Холла и эффект Гаусса. [31]
Рассмотренный эффект увеличения сопротивления полупроводника за счет снижения подвижности носителей тока известен в литературе [6-1] под названием эффекта Гаусса. [32]
Построение элементов базируется на новых методах и явлениях: люминесценции, сверхпроводимости, пьезомаг-нитных, оптоэлектронных, квантовых, полупроводниковых, электрохимических, эффектах Гаусса, Холла и др. Большое внимание уделяется совершенствованию лазерных методов измерений, созданию элементов с переменной структурой, повышению точности с помощью вычислительной техники. Существенное практическое значение имеют поперечный акустоэлектрический эффект, новые исследования по распространению радиоволн в далеком космосе и др. Проводятся дальнейшие работы по изысканию и использованию других новых принципов измерений. [33]
Использование полупроводников с более высокой подвижностью носителей тока, чем у Bi ( InSb, InAs), безусловно может значительно расширить применимость измерителей магнитных полей, основанных на эффекте Гаусса. [34]
Разработкой, изготовлением и применением как самих магниторезисторов, так и устройств с такими преобразователями занимаются многие организации. Использование эффекта Гаусса освещено в специальной литературе по физике твердого тела, а также в ряде работ по использованию эффекта Холла. К ним относятся работы В. Н. Богомолова, Н. И. Овчеренко, обуса, Я. [35]
Отечественная промышленность серийно выпускает кремниевые, германиевые и арсенид-галлиевые преобразователи Холла. В магниторезисторах используется эффект Гаусса, суть которого заключается в изменении сопротивления проводника или полупроводника с электрическим током при внесении их в магнитное поле. [37]
Магниторезистор — резистор, основное свойство которого заключается в способности изменять сопротивление при изменении воздействующей на него магнитной индукции. Принцип действия магниторезистора основан на использовании эффекта Гаусса, заключающегося в изменении сопротивления проводника с током при внесении его в магнитное поле. Изменение сопротивления полупроводниковой пластины с re — электропроводностью, помещенной в магнитное поле, происходит в результате того, что удлиняется путь, проходимый электронами. Удлинение пути электронов вызвано действием силы Лоренца. [39]
Для снижения температурных влияний применена схема температурной компенсации с термосопротивлением типа ММТ-54, смонтированным в преобразователе в непосредственной близости к пластинке германия. При больших индукциях линейность шкалы прибора нарушается вследствие эффекта Гаусса. Для уменьшения этого влияния на пределах выше 0 3 тл измерительный прибор шунтируется сопротивлениями. Сопротивления на каждом пределе подобраны так, чтобы в начале шкалы прибор имел положительную погрешность, а в конце шкалы — отрицательную, но при этом не выходил из своего класса точности. [40]
Гальваномагнитными называются эффекты, сущность которых заключается в изменении физических свойств проводников или полупроводников при протекании через них электрического тока и одновременном воздействии на них магнитного поля. К ним относятся эффект Холла, магниторезистивный эффект ( эффект Гаусса), эффект Зттингсгаузена. [41]
При внесении проводника или полупроводника, по которому течет электрический ток, в магнитное поле меняется его сопротивление. Этот эффект связан с действием сил Лоренца и называется эффектом Гаусса. [42]
Для измерения индукции переменного магнитного поля могут быть использованы компараторы с гальваномагнитными преобразователями, обладающими малой частотной погрешностью. Положим, что в компараторе разновременного сравнения применен преобразователь, основанный на эффекте Гаусса. Преобразователь включают в одно из плеч моста постоянного тока и помещают в переменное поле, индукцию которого требуется измерить. Мост уравновешивают с помощью сопротивлений других плеч. Затем преобразователь переносят в постоянное поле и, изменяя его индукцию, снова добиваются равновесия моста, не меняя сопротивлений остальных плеч моста. В данном эксперименте используется косвенный метод сравнения замещением. Тогда индукция переменного поля ( среднеквадратическое значение) будет равна индукции постоянного поля. [43]
Значение шумов резко возрастает при использовании высоко-омных полупроводниковых материалов. У таких материалов носители тока имеют обычно малую подвижность. Частотная зависимость эффекта Гаусса определяется временем, которое как для малых, так и для больших подвижностей носителей тока составляет 10 — — 10 — 13 сек. [44]
В книге рассмотрены характеристики и основные свойства гальваномагнитных преобразователей, использующих эффект Гаусса. Приводятся данные о полупроводниковых материалах и технологии изготовления магниторезисторов. Описаны разработанные приборы и схемы, использующие эффект Гаусса. Изложены основы работы, особенности конструирования и применения магниторезисторов. [45]
Страницы: 1 2 3 4
www.ngpedia.ru
